Параметрический анализ в задачах математического программирования

Вполне очевидно, что возможность исследования зависимости решения задачи математического программирования от значений ее параметров представляет собой важный инструментальный компонент математического моделирования. Хотя сложность такого исследования, обусловленная практической невозможностью непосредственного использования аналитических методов, равно как и специфическими особенностями объекта исследования: определенностью не на. всем множестве допустимых значений параметров, а. также возможным отсутствием функциональности и гладкости на. этом множестве, является существенным фактором, ограничивающим его применение.

Статья [1] содержит описание и теоретическое обоснование метода, анализа, зависимости решения задач линейного программирования от параметров, основанного на. построении ее функциональной (однозначной) сглаженной аппроксимации, близкой по своим значениям к исследуемой зависимости при тех параметрах, для которых последняя существует. В статье [2] исследуются вычислительные аспекты предложенного алгоритма. В настоящей статье рассматривается расширение этого подхода на случай выпуклого нелинейного программирования, а. также анализируется проблема, получения решений с достаточно высокой точностью.

Описание подхода

Рассматриваемый подход основан на. нестандартном использовании метода, гладких штрафных функций [3], точнее, на. некоторых специфических свойствах специального класса, функций штрафа, описанных ниже.

Введем обозначения ж € Е^п, Л € Е^т, u € Е^к с координатными представлениями вида ||ж|| = ||^1^2 ...£n||^T, ||Л|| = ЦА1А2 .. .Am||^T, ||u|| = ІІН1Н2 . ..V k ||T, при чем u € Q □ Е^к.

В настоящей статье предлагаемый метод используется для анализа, зависимости от параметров решения следующей нелинейной задачи математического программирования:

при фиксированном u € Q С Ек максимизировать по {ф,^2,..., (,,} выпуклую вверх по ж € Еп и достаточно гладкуто 1 целевую функцию F(ж, u)

при условиях: ^ j >  0 V j = [1, п] и /фж, u) 6 0 V г = [1, m], где функции /фж, u) V г = [1, m] достаточно гладкие и такие, что множество, определяемое данными условиями, выпукло по ж € Е^п, во всех случаях, когда оно не пусто.

Эту задачу для краткости будем именовать «М-задачей» и обозначать как М, а ее решение при фиксированном n € И обозначать х * (п). Анализ зависимости х * (п) от вектора параметров n € И К Е ^k и составляет основной предмет исследования настоящей статьи.

Вначале кратко изложим схему предлагаемого подхода для пары линейных взаимодвой-ственных задач, записанных в следующей симметричной форме.

Пусть прямая задача линейного программирования имеет вид:

максимизировать по {ф, £2,..., ^п} F(х, n) = ]l"=| c j(n)£j при условиях: ^j > 0 V j = [1, п] и /і(х,п) = —Д(п) + ^"=1 ач (n)^ j 6 0 Vг = [1,т]. Эту задачу для краткости будем именовать «P-задачей» и обозначать как Р, а ее решение при фиксированном n € И обозначать х*(п).

«D-задача», двойственная к Р, будет соответственно иметь вид:

минимизировать по {Ai, A2,..., Am} G(M,n) = £i=i Mn^Ai при условиях: Ai > 0 Vг = [1,т] и gj(Л, n) = —Cj(n) + ]уф=| aij(n)Ai > 0 Vj = [1,п]. Ее решение при фиксированном n € И будем обозначать Л* (и). Все функции оу(n),/3i(n) и aij(n) в условиях задач Р и D предполагаются известными.

Определим штрафную функцию Р(т, s) так, чтобы она существовала и была непрерывна вместе со своими производными до второго порядка включительно для всех s и любых т > 0, а также удовлетворяла условию lim Р(т, s) = I 0 ПрИ S> °’                            (1)

т — +0          [ +^ пр и s <  0.

Функция Р(т, s) может использоваться в качестве «штрафа» за нарушение связи вида s > 0 в экстремальных задачах с ограничениями-неравенствами, потребуем при этом, чтобы она удовлетворяла условиям дР< 0,   ^> 0,

os           os2

ЭР           1                                    S         ЭР (s\ а д^ являлась фуиктщеп только одного аргумента у- то есть д^ = Ф (у)-

Как известно [4], стандартный метод гладких штрафных функций позволяет в случае однозначной разрешимости задачи Р находить ее решение в виде x*(n) = lim х(т, n), где т —— +0

х(т, n) =argmax А_р(т, х, n), для А_р(т, х, n) = F (х, n) — ]уф=і Р(т, (—f_i (х, n)). Ж

Аналогично, решение задачи D может быть представлено в виде Л * (п) = lim Л(т,n), где т — +0

: "=i ^{Р (т} , ⁽g j ^{(л ,п ))}.

Л(т, n) =argmin А д (т, Л, n), и А д (т , Л, n) = С(Л, n) + ^

л

В этом случае, штрафа (1) х(т, n) висимостей x*(n) и grad^ А р (т, х(т, n), n)

как показано в [5], для достаточно широкого класса функций и Л(т, n) можно использовать в качестве аппроксимаций за-Л*(п), поскольку они удовлетворяют условиям стационарности = о и gradл Ад(т, Л(т, n),n) = о, к которым применима теорема о неявных функциях [6]. Кроме того, в случае однозначной разрешимости задач PhD оказываются справедливыми равенства

ЭР

V г = [1, т],

V j = [1,п],

^A*⁽ⁿ⁾ = ^{— lim}_n"d7^{(т, —} / і ^{( х ( т,п )))} т — +0 OJ_i

ЭР ,

^*(n) = — lim A-^gj (Мғ^) j        т—+0 ogj которые являются условиями, связывающими решения задач PhD.

В рассматриваемом подходе в качестве аппроксимаций зависимостей х*(п) и Л*(п) предлагается использовать не х(т, n) и Л(т, n), а функции х(т, n) и Л(т, n), определяемые систе мой условий

^Ai⁽ⁿ⁾ = ^— дР^(т, ^— / і ^{( х ( т,п )))     v г} = ^[1,т],

^з ⁽ⁿ⁾ = ^— дР ^(т,gj ^{(Л( т,п )))       V j} = ^[1,п]

и для которых (как показано в [1]) также оказываются справедливыми равенства

ж* (и) = lim ж(т, и)      и     Л*(и) = lim Л(т, и).

т ^+0                                 т > ■ о

Наконец, систему (3) можно записать в более удобном (для совместного решения задач Р и D) виде, если учесть, что функция д? (^в силу условий (2)) имеет обратную Q(т,s) = Ф^-1 ( ту. ⁸

3 , (и) - Е а ,, (и)£, = Q ( t,X , )    V г = [1,m],

<           зД      _           _                                 (4)

-О , ^(и) + Е⁽Щ ^(и)^Х , = ^Q(T,^ i ^{)    V}3 = ^[1,<

,=1

Теперь выясним, как будет выглядеть система вспомогательных уравнений (4) в случае нелинейной задачи М. Предположим, что ж* (и) — оптимальное решение задачи М, существует, и построим линейную аппроксимацию условия этой задачи в некоторой, достаточно малой окрестности ж*(и). Возможная негладкость ж*(и),и € П, на данном этапе существенной роли не играет.

Результат этой линеаризации выглядит следующим образом.

Целевая функция, подлежащая максимизации, имеет вид

” ЭЕ                          " ЭЕ         " ЭЕ

Е(х*(и),и) + о-, - ^*(и)) = I Е(ж*(и),и) - 52 щЕ"1 I + 52 э^ , j=i °Сз                                   j=i °Сз /    j=i °Сз а ограничения-неравенства соответственно d/

/,(ж*(и),и) + £ ^((, - е*(и)) 6 0

V г = [1, m]

или же д/           дД

Л(жЧи).и) - £ д' дЫ + £ 'е, 6 0.

з=1 3,3              з=1 3,3

В вышеприведенных формулах все частные производные вычислены при ж = ж*(и). Заметим также, что при использовании обозначений

ЭЕ         д/                       ™ д/

— = ст,^(и), — = ^а -з ^(и)   л  /,^(ж*^(и),и) -22 _;i,E'^{n   -}А^(и)

°Сз              °Сз                                  з=1 °Сз эти соотношения являются формулировкой задачи, эквивалентной задаче Р.

Теперь для линеаризованной задачи М записываем формулировку вспомогательной системы уравнений (3):

'         и Ә/ і-

-3, + Е ^Е, = -Q(t,X,)    Vг = [1,m] , з=1 дез

ЭЕ ™ Ә/,-           -

^{- Е} лД^Х- = ^{- Q ( t,C} 3 )    ^V3 = ^[1,n] .

о^ з ,=1 о^ з

Здесь оказываются существенными следующие два обстоятельства. Во-первых, левые части первой группы уравнений в этой системе, являющиеся линейными аппроксимациями функций /,(ж,и), следует заменить самими этими функциями, поскольку при построении системы (4) вид первой группы ее уравнений не зависит от того, являются ли функции /,(ж,и) линейными или нет. Значит, в системе, обобщающей условия (4) на нелинейный случай, первая группа уравнений будет иметь вид /,(ж, и) = - Q(t, Х,) V г = [1,m].

Во-вторых, можно заметить, что левые части второй группы уравнений суть координаты градиента (взятого по компонентам ж) функции Лагранжа для задачи М.

Это в своей совокупности позволяет заключить, что обобщением системы уравнений

(4) на случай задачи М будет система уравнений вида

Ф г ^(ж,и) д" (^ғ(ж, и) — £ ХіМғ^и)^

-Q(т,Хi) V г = [1,т],

—Q(т^t j ) V j = [1,n]

или же, учитывая, что стандратная функция Лагранжа для нелинейной задачи М имеет т вид L(ж(и), Л(и)) = F(ж, и) — 52 Хtфt(ж,и) , в более компактной форме t=i dL _ dx (ж,Л) dL _

. < (Ж,Л)

^Q(T, ^Х г )

^{— Q(}T^,l j )

V г = [1, т] ,

V j = [1,п] .

Еще раз обратим внимание, что значения функций и производных в этой системе вычисляются на элементах ж € Е ^п и Л € Е^т, которые являются неизвестными. Отыскание значений этих неизвестных как функций коэффициента штрафа т и вектора параметров и является основной задачей, решаемой в рамках предлагаемого подхода.

Аналогично тому, как для системы уравнений (4) в [1] рассматривалась вспомогательная функция, представляющая собой сумму стандартной функции Лагранжа для пары пт задач Р и D и корректирующего слагаемого вида 52 R(т, ^j) — 52 R(т, Хг) , для системы "=1г=1

уравнений (5) введем вспомогательную функцию вида тпт

и(тж,Л,и) = ғ(ж,и) — ^ Хг/г(ж,и) + ^ R^T, Cj) — ^ ^т Хг) , г=1               j=iг=1

dR где ds (T,S) = Q(r,s).

Исследуем теперь свойства функции (6).

Теорема 1. Если ж(т, и) и Л(т, и) - решения системы (5), то {ж(т, и),Л(т, и)} - стационарный вектор функции U(т, ж, Л, и) в Е^п 0Е ^т.

Доказательство.

Дифференцируя функцию (6) по ф, £₂₎ • • • £_п и Хц Х₂, ••• Х_т, получаем

dU дХГ dL = —- — Q(т, Хг) = —/г(ж, и) — Q(т, Хг) Vг = [1, т] , дХг ф^ = d^ + Q(т,^j) Vj = [1,n] , что в силу соотношений (5) дает при ж = ж(т, и) и Л = Л(т, и)

dU ду = —/г(ж,и) — Q(т,Хг)=0 V г = [1,т] , dU dL = ^—— Q(т,Хг) = 0 V j = [1,п] . d^j   дХг

Теорема доказана.

Теорема 2. Пусть точка {х*(и); Л*(и)} ограниченная, тогда найдется А > 0 такое, что V т : 0 < т <  А в Е^п 0 Е^m существует окрестность элемента {х(т, и), Л(т, и)} такая, что этот элемент - седловая точка функции U(т,х, Л, и)

Доказательство.

Согласно лемме 1 в [1], доказанной без каких-либо предположений о линейности исходной задачи, lim П(т, s) = 0 V s > 0 . т м+0 п         m

Поскольку U(т, х, Л, и) = L(x, Л, и) + 52 ^(т, ^ j ) — 52 ^(т, -г) , а для функции Лагранжа j =1            г=1

в условиях теоремы lim L(x(т, и), Л(т, и), и) = L(x*(u), Л*(и), и) , т м ■ 0

то из непрерывности U(т,х(т,и), Л(т,и),и) по т и известного факта, что точка {х*(и);Л*(и)} — седловая для функции Лагранжа, следует утверждение теоремы.

Теорема доказана.

Теорема 3. Пусть точка {х*(и);Л*(и)} ограниченная, тогда Vг = [1,т] справедливы равенства — «условия дополняющей немсесткости»:

lim Хг(т,и)Д (х(т,и),и)) = 0 .

т м ■ 0

Доказательство.

Из условия (2) ^у = Ф ( т ) ¹¹ определения фупкщш Q(т, s) как обратиои к — д^ следует, что Q(т, s) = т ^(s), где функции Ф(s) и Ф(s) взаимно обратные, причем ограниченные для любого конечного s.

Поэтому для г, соответствующих активным ограничениям,

^^^^.

lim Х г (т,и)ф г (х(т,и),и)) = т м ■ 0

—

lim Х_г(т, и т м +0

^)Q У- Х г ^(т,и)

= — lim тХ_г(т, и)Ф (Х_г(т, и)) = 0 .

Теорема доказана.

Для доказательства аналогов теорем 3 и 4 из [1] линейность исходной задачи не требуется, поэтому их утверждения справедливы и для случая задачи М.

Использование рассматриваемого подхода проиллюстрируем следующим примером.

Пример 1. Максимизировать функцию Ғ = —(^1 — а)² — (^₂ — Ь)²

при условиях ^1 > 0 ; ^2 > 0 ; ^1 + 2^2 6 3 11 ^2 — ^2 6 0 .

Решение. Вспомогательная система уравнений (5) (с учетом изменений, аналогичных сделанным при переходе от системы (15) к системе (17) в [2]) для данной задачи имеет вид

_ _

-3+ |€ 1 | + 2|< 2 |

2(|A 1 |

-

и)'

іё і і ² -К2 І

^-2 (|f i | - a) ² - ¹ А і | - 2 ^|£J • ^| Л 2^|

2(м

-

'

^{-2( 1} € 2 ^{1 - Ь)2 - 1} A i^{1 - 21} £ 1¹ • ¹ Л 2¹

і(ы-

й-

■:(

^^^^.

l€ 2 |

-

Й-

Задача имеет выпуклую вверх целевую функцию, определенную на выпуклом допустимом множестве при любых значениях параметров a и Ь. Ее решения, полученные при различных коэффициентах штрафа т, приведены в таблицах 1-5. Всего рассмотрено пять вариантов с различной структурой оптимального множества активных ограничений. Каждый вариант пронумерован арабскими цифрами в круглых скобках, предваренными символом Д. Соответствующая изолиния целевой функции показана штриховой линией и выделена определенным цветом.

В большинстве случаев решения задачи М очевидны (легко проверяются графически, см. рис. 1), но для некоторых значений параметров подобная проверка может представлять определенную проблему. Например, при a ■ 1 и Ь ■ 0 (см. табл. 4) точное оптимальное значение A2 является корн ем уравнения A2(A2 + 1)² - 2 ■ 0 и равно

28+ 3^87 - 1)

²) / (з 3/ 28 + 3V87)

0.69562077 .

Другой проблемой может являться медленная сходимость к решению системы (5), вызванная ухудшением обусловленности задачи при уменьшении значения коэффициента штрафа т (как, например, в варианте, приведенном в таблице 5) при т <  10^-5. Стоит также отметить, что в варианте Д(5) задача М оказывается переопределенной.

Таблица 1

Вариант #(1) при a ■ -1 и Ь = 2

Значение коэфф, штрафа т	€1	€2	А1	А2
0.1	0.019369832	1.457551752	0.540297817	0.034272627
0.01	1.993374914*10 -3	1.495306682	0.504298833	3.343767165*10 -3
0.001	1.999333755*10 -4	1.499525574	0.500432983	3.334387665*10 -4
0.0001	1.999933338*10 -5	1.499952506	0.500043330	3.333438877*10 -5
0.00001	1.999993333*10 -6	1.499995250	0.500004333	3.333343889*10 -6
0.000001	1.999999333*10 -7	1.499999525	0.500000433	3.333334389*10 -7
0.0000001	1.999999933*10 -8	1.499999953	0.500000043	3.333333439*10 -8

Таблица 2

Вариант #(2) при a ■ 1 и Ь = 2

Значение коэфф, штрафа т	€1	€2	А1	А2
0.1	0.583548042	1.198338239	0.821611165	0.058091273
0.01	0.598042642	1.199867650	0.802184510	5.936533717*10 -3
0.001	0.599800647	1.199987317	0.800218561	5.950774255*10"-4
0.0001	0.599980028	1.199998737	0.800021857	5.952220054*10"-5
0.00001	0.599998002	1.199999874	0.800002186	5.952364860*10 -6
0.000001	0.599999800	1.199999987	0.800000219	5.952379343*10"-7
0.0000001	0.599999980	1.199999999	0.800000022	5.952380791*10 -8

Таблица 3

Значение коэфф, штрафа т	€1	€2	А1	А2
0.1	0.974069007	0.968103086	0.446274903	0.825513741
0.01	0.997047324	0.996317696	0.405095735	0.802789972
0.001	0.999700482	0.999625692	0.400515343	0.800281696
0.0001	0.999970005	0.999962507	0.400051593	0.800028197
0.00001	0.999997000	0.999996250	0.400005160	0.800002820
0.000001	0.999999700	0.999999625	0.400000516	0.800000282
0.0000001	0.999999970	0.999999963	0.400000052	0.800000028

Вариант #(3) при а = 2 и Ь = 1

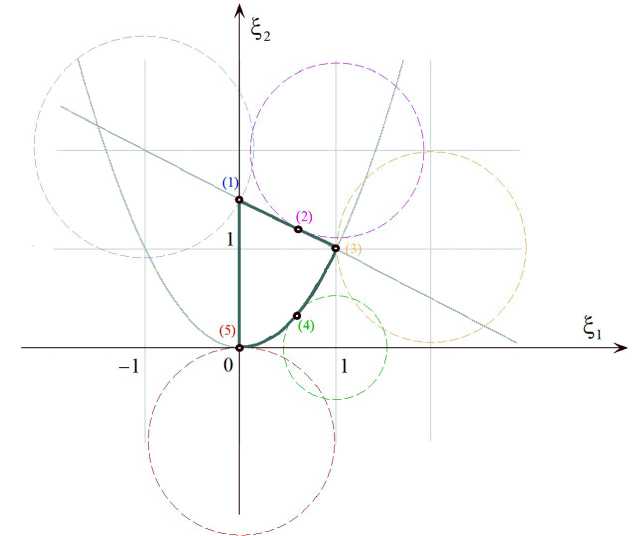
Рис. 1. Графическая интерпретация задачи М (из примера 1).

Таблица 4

Значение коэфф, штрафа т	€1	€2	А1	А2
0.1	0.590384707	0.382763237	0.030383906	0.714803394
0.01	0.590024813	0.351817238	2.930221987*10 А-3	0.697042081
0.001	0.589784721	0.348216783	2.917524171*10 А-4	0.695755291
0.0001	0.589757566	0.347851082	2.916233632*10А-5	0.695634142
0.00001	0.589754818	0.347814455	2.916104368*10А-6	0.695622106
0.000001	0.589754543	0.347810792	2.916091440*10 А-7	0.695620903
0.0000001	0.589754515	0.347810425	2.916090147*10 А-8	0.695620783

Таблица 5

Значение коэфф, штрафа т	€1	€2	А1	А2
0.1	0.115087159	0.037662406	0.017790571	0.785205278
0.01	0.037312698	4.029110057*10А-3	1.692254947*10 А-3	0.770494044
0.001	0.011862237	4.059161908*10 А-4	1.673737642*10А-4	0.769365417
0.0001	3.756483220*10А-3	4.062681549*10 А-5	1.668801473*10А-5	0.769400400
0.00001	1.188404667*10А-3	4.063189420*10 А-6	1.667331671*10 А-6	0.769451061
0.000001	X	X	X	X
0.0000001	X	X	X	X

Построение точного решения

Как показано выше, сглаженные зависимости ж(т, и) и Л(т, и) обладают рядом свойств (таких, как существование во всем пространстве параметров, однозначноств и гладкоств), позволяющих эффективно их использовать в классических схемах решения параметрических задач. Однако их значения отклоняются от значений ж* (и) и Л* (и), хотя и близки к ним при малых положительных т в силу соотношений

ж* (и) = lim ж(т, и)      л     Л* (и) = lim Л(т, и) .

т ^+0                                   т > ■ о

Поэтому представляет практический интерес вопрос о том, как оценить при помощи ж(т, и) II Л(т, и) значения зависимостей ж*(и) іі Л* (и) для тех зшгчешш параметров и. при которых последние существуют.

Вполне очевидная возможность повышения точности сглаженных аппроксимаций ж(т, и) и Л(т, и) за счет уменьшения значения т с практической точки зрения имеет ограниченную область применения, так как обусловленность системы уравнений (5) ухудшается по мере уменьшения т. Это следует непосредственно из условия (1), формально описывающего основное свойство штрафной функции. Поэтому для получения оценок значений ж* (и) и Л* (и) с необходимой, достаточно высокой точностью воспользуемся другой схемой, не требующей решения системы (5) при очень малых значениях коэффициента штрафа т.

Предположим, что вектор {ж*(и),Л*(и)} существует для некоторого фиксированного и. Поскольку для каждого достаточно малого т € (0, то] функция (6) имеет единственную седловую точку {ж(т, и), Л(т, и)}, то в пространстве Еп0Ет определена траектория (линия) (рис. 2а), для точек которой справедливы равенства (5) и имеет место асимптотическое приближение {ж(т, и), Л(т, и)} к {ж*(и), Л*(и)} при т ^ 0 + 0. При этом, как показано в [5], из условий (2) и системы уравнений (5) следует, что зависимости ж(т, и) и Л(т, и) являются достаточно гладкими функциями не только параметра и, но и коэффициента т. Тейлоровские аппроксимации этих зависимостей в окрестности некоторого значения т имеют вид дж                                  _ д .Л

ж(т + Ат, и) = ж(т, и) + — Ат + о(Ат)  1і ж(т + Ат, и) = Л(т, и) + — Ат + о(Ат) .

Если в этих соотношениях перейти к пределу при Ат ^ —т + 0 и учесть соотношения (7), то получаются следующие оценки для ж* (и) и Л* (и) :

^^^^в

ж* (и) = ж(т, и) — — т + о(т) дт

II Л* (и) = Л(т, и) — т + о(т) . дт г->                                        Вт,

Значения производных др

и

функциях [6], примененной к

^^^^в

дЛ дт

могут быть найдены при помощи теоремы о неявных

системе уравнений (5). Для их вычисления необходимо ре

Вариант #(4) при а = 1 и Ь = 0

Вариант #(4) при а = 0 и Ь = —1

шить систему линейных уравнений

V „д²Ц ^д^ з ₊ V д²и дА, = _— д ²U ^=1 д^д^ Дт ⁺ »= д^ідА» Дт    д^дт

V t = [1,п],

V г = [1,ш].

V „д²U ^д^з ₊ V Д' Д = _— д²U ^=1 дА_г д^і дт »=1 дА_г дА» дт     дА_г дт

Соотношения (8) позволяют построить итерационную процедуру (аналогичную предложенной в [7] процедуре «многошаговой экстраполяции») последовательного уточнения значений сглаженных оценок для зависимостей ж(т, и) и Л(т, и), сходящуюся к значениям ж*(и) и Л*(и) там, где последние определены однозначно.

Уточнение сглаженного решения на первом шаге этой процедуры выполняется по очевидным формулам

Лі(и) = Л(т,и) —

дЛ дт т.

ж1(и) = ж(т, и) — —— т II дт

Геометрическая интерпретация процедуры линейной экстраполяции показана на рис. 2а. Если коэффициент штрафа т достаточно мал, то в силу свойств тейлоровской аппроксимации отклонение {жі (п), Лі(п)} от {ж*(п), Л*(п)} будет меньше, чем отклонение {ж(т, п), Л(т, п)} от {ж*(п), Л*(п)}.

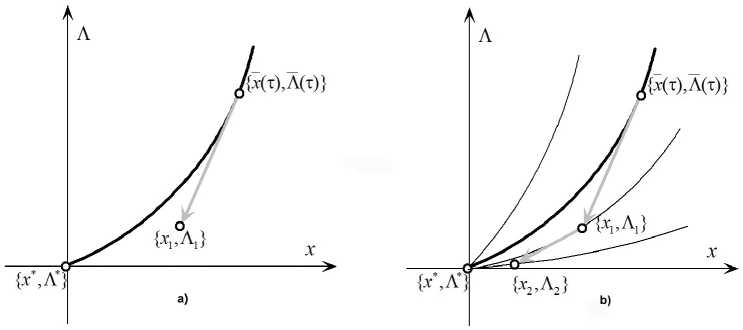
Рис. 2. Траектории сходимости метода экстраполяции {ж(т, п), Л(т, п)} при т ^ 0 + 0

Если полученная точность оказывается неудовлетворительной, то возможно выполнение дополнительных шагов, аналогичных первому.

Предварительно, модифицируем функцию U(т, ж, Л, п), не меняя ее основных свойств, так, чтобы точка {жі(п), Лі(п)} оказалась для нее стационарной. Уединим в функции U (т, ж, Л, п) слагаемые, яви о зависящие от т, и предположим, что этот параметр может иметь в выделенных слагаемых значения дх,т и длгт, где дх, и длг - некоторые константы. Тогда модифицированная вспомогательная функция будет иметь вид п            m

U(т,ж,Л,п) = и0(ж,Л,п) + ^к(д$3т,у) - ^К(длгт, А.) , j=і               i=i где Цфж, Л, п) — сумма слагаемых в функции (6), не зависящих от т. Теперь подберем значения величин дх, и длг так, чтобы gradxU (т,ж1 (п), Л1(п),п) = о     и     gradЛ U (т,ж1(п), Л1(п),п) = о.

Поскольку в силу условий (2) уравнения системы (5) линейны по т, то искомые значения д х , и д л _г будут равны

m

-^j(п) +    «ij (п)Хц д<, =          т ^T(hi)              V 3 = [1,n],

п

• 9 . («) ^- У «.j (^п+

• ^длг = -------7ЩД------- ^{V 1} = ^[1, ™1.

В этом случае точка {жі(п), Лі(п)} оказывается принадлежащей другой траектории (рис. 2Ь), но также асимптотически приближающейся к {ж*(п), Л*(п)} при т ^ 0 + 0. И в этой точке возможно повторение вычислений по формулам, аналогичным приведенным выше:

ағ                                    а л

• ^ 2j (п) = F ij (п) -       т і V 3 = [1,п] И    Л2. (п) = Л_н (п)--д^ ті V1 =[1,^].

Величина параметра ті, соответствующая точке {жі(п), Лі(п)} на новой траектории, зависит от способа параметризации этой траектории и может выбираться достаточно произвольно, лишь бы сохранялась сходимость к {ж* (п), Л*(п)} пр и т ^ 0 + 0. В данной статье

Т 1 полагается равным порядку модуля раз пости значений пулевых функций задал PhD в точке {х1(и),Л1(п)}. Значения производных по параметру т находятся из системы (9), в которой функция U ( т,х, Л, и) заменена на U ( т,х, Л, и).

Описанная процедура может итеративно повторятвся до получения приемлемой точности решения. Ее сходимость в достаточно малой окрестности {х*(и), Л*(и)} доказана в [7]. Следует отметить, что применение этой процедуры в многоуровневых параметрических методах оправдано лишь после получения оптимального решения в пространстве параметров, поскольку уточнять промежуточные оценки данного решения заведомо нецелесообразно.

Продемонстрируем применение итерационной процедуры уточнения приближенного решения, полученного для параметрической задачи из примера 2 в [2] .

Пример 2. Максимизировать в Е ⁴ функцию F = 2€1 + 3^2

при условиях

€1 > 0 , ^2 > 0 II- 1 6 €з 6 6 ,   -1 6 €4 6 6 ,

• ¹      , 22/          2    ^³    5 ,     2          5

€1 + (2<3 + €4 - 1)2^2 6 6 ,     (€з - 2^4 + 1)2^1 + €2 6 6 , решение которой имеет вид:   €* =6 , €* =6 , €3 = 5 , €4 = 5 , F* = 30.

В качестве начального приближения примем приведенное в таблице 5а [2] решение этой задали при т = 0.01:

_9 = 0.200000000,    q = 0.600000000,

€1 = 6.007316932, €[2 = 6.013170760,

Ах = 1.970795734, [2 = 2.970765654.

В данном примере для модифицированной вспомогательной функции U ( т,х, Л, и) равенства, используемые для определения значений g_Xj и дл^ имеют вид

2 - А1 - (р - 2q + 1)2^А2 - д ^ 2

(А

-

У

=0,

Результаты расчетов приведены в таблице 6. Степень погрешности определялась по величине модуля разности значений целевых функций прямой и двойственной задач. Величина этой погрешности также использовалась для оценки текущего значения коэффициента т.

Таблица б

Результаты вычислений по методу линейной экстраполяции

И	£ Т	А Г	А Г	IF - G|	т	9 ^ 1	9 ^2	9 X 1	9 X2
6.007316932	6.13170760	1.970795734	2.970765654	0.40477	1е - 02	1.00	1.00	1.00	1.00
6.000183847	6.000163106	2.000036654	3.000066837	0.00023	1е-04	-0.13	-0.23	2.45	1.22
5.999999994	5.999999995	1.999999999	2.999999998	6.2е-09	1е-09	0.41	0.66	-7.49	-3.41
6	6	2	3	0	0	-	-	-	-