Параметрический синтез амплитудно-фазовых модуляторов с заданным количеством одинаковых каскадов типа «нелинейная часть - комплексный четырехполюсник»

В работе [1] сформулирована задача и разработан алгоритм параметрического синтеза согласующих четырехполюсников различных типов (реактивных, резистивных, комплексных и смешанных) по критерию обеспечения заданных частотных характеристик многокаскадных амплитудно-фазовых модуляторов (АФМ). В частности, решена задача синтеза АФМ с использованием одинаковых каскадов типа «нелинейная часть (НЧ)-реактивный четырехполюсник».

Цель данной работы состоит в изменении областей физической реализуемости заданных характеристик АФМ путем использования произвольного количества N одинаковых каскадов типа «НЧ – комплексный четырехполюсник (КЧ)»

между источником сигнала с сопротивлением z 0 = ^r 0 + jx 0 и нагрузкой z H = ^r H + jX (рисунки 1, 2) и специального выбора параметров КЧ.

Каскады соединяются между собой с использованием того вида обратной связи, по которому соединены нелинейный элемент (НЭ) и цепь обратной связи (ЦОС) (параллельной или последовательной по току или напряжению).

Основные положения теории синтеза, которые использованы при получении результатов, изложены в работах [2; 3]. Оптимизация параметров двухполюсников, не входящих в КЧ, осуществляется с помощью известных численных методов [4] по критерию обеспечения заданной рабочей полосы частот. Все обозначения неописанных величин и аббревиатур в данной статье соответствуют принятым в [1].

а

б

в

а

б

в

Рисунок 3. Примеры синтезированных КЧ

1. Результаты параметрического синтеза

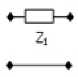
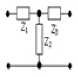
Для примера здесь приводятся некоторые из решений, полученных для типовых схем КЧ и схемы АФМ (рисунок 1, а ). Если в качестве КЧ используется последовательно включенный комплексный двухполюсник (рисунок 3, а ), то зависимость его сопротивления Z ₁ от частоты определяется следующим образом:

Рисунок 4. Примеры синтезированных КЧ (продолжение)

3. Математическое и схемотехническое моделирование амплитудно-фазовых модуляторов с одинаковыми каскадами типа НЧ – КЧ

Z _ —A.

1B

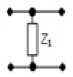
Параллельно включенный комплексный двухполюсник с сопротивлением Z ₁ (рисунок 3, б):

Z1 =

C

.

1 - A

На рисунках 5–12 для примера показаны принципиальные и эквивалентные схемы однокаскадного и двухкаскадного АФМ, соответствующие исследуемой структурной схеме с параллельной по напряжению связью, представленной на рисунке 1, а , а также их теоретические и экспериментальные характеристики. Использован транзистор типа BFQ17PH (рисунки 5, 7). Схема НЧ выполнена в виде параллельно соединенных транзистора и ЦОС (П-образного соединения трех элементов C 78 , R 105 , R ₁₁₀) на однокаскадной схе-

ме ^{(рисунок 5)} и ^C 78 , R 105 , ^R iio , ^C 83 , R 125 , ^R 126

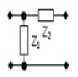
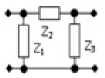
Г-образное соединение двухполюсников Z ₂ (рисунок 3, в ):

Z ₁ и

Z _ Z 2 C ; z _

¹ A + BZ ₂ - 1      ²

Z1 (1 - A) - C

BZ ₁ - 1

.

Обратное Г-образное соединение двухполюсников Z ₁ и Z ₂ (рисунок 4, а ):

Z _ Z 2 (1 - A) - C ; Z _

¹      A + BZ ₂ ;     ²

C + AZ1

1 - A - BZ1

.

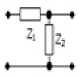
Т-образное соединение двухполюсников Z ₂ и Z ₃ (рисунок 4, б ):

Z _ Z2 (1 - A - BZ3) - C + Z3

1 =     A + B (Z 2 + Z3)     ;

Z 1 и

Z 2 =

Z3 - C - Z1 (A + BZ3)

Z 2

^Z з

-

A + B (Z1 + Z3) -1 ;

C - A (Z1 + Z2) - BZ1 Z2

B (Z1 + Z 2) -1

.

П-образное соединение двухполюсников Z ₂ и Z ₃ (рисунок 4, в ):

Z ₁ и

Z1 =

Z

Z 2 Z3 - C (Z 2 + Z3)

C - Z3 + A (Z2 + Z3) + BZ2 Z3 ;

_ Z 1 Z3 (1 - A) - C (Z1 + Z3)

' 2 ^_

Zз =

C - Z3 + AZ1 + BZ 1 Z3 ;

(Z1 + Z 2 )C+ AZ1 Z 2

Z 1 (1 - A - B Z 2) - C + Z 2

.

на двухкаскадной схеме (рисунок 7). Нагрузка и сопротивление источника сигнала выполнены на элементах R ₁₁₄ и R ₁₁₇ соответственно. Схемы КЧ собраны в виде Г-образного четырехполюсника на элементах R ₁₂₀, R ₁₂₁, C ₇₉, L 2 (рисунок 5), R ₁₂₀, R 121 , C 79 , L 2 , R 129 , R 130 , C 84 , L 4 (рисунок 7), параметры которых определялись по формулам (3). Эквивалентная схема нелинейного элемента выполнена в виде перекрытого Т-образного четырехполюсника на элементах R ₁₀, L 6 , R ₁₃, L ₇, R 11 , L 9 , R 9 , L ₅ (рисунок 10, 11). Параметры эквивалентной схемы НЭ выбраны из условия совпадения выходного сопротивления НЧ с выходным сопротивлением НЧ с использованием реального транзистора [2]. Схема НЧ реализована в виде параллельно соединенных эквивалентной схемы нелинейного элемента и цепи обратной связи из П-образного соединения трех элементов C 8 , R 19 , R 22 -

Параметры ЦОС заданы произвольно. Схема КЧ собрана на основе Г-образного соединения четырех элементов R ₂₄, R ₂₃, L 8 , C ₉ .Частотные характеристики принципиальных схем, показанных на рисунках 5 (сопротивления источника сигнала и нагрузки равны 100 Ом) и 7 (сопротивления источника сигнала и нагрузки равны 50 Ом), идентичны. Это соответствует выводам, сделанным на основе анализа полученных выше выражений для передаточных функций исследуемых структурных схем (рисунок 1, а ). Анализ также показывает, что экспериментальные (рисунок 6, а , б )

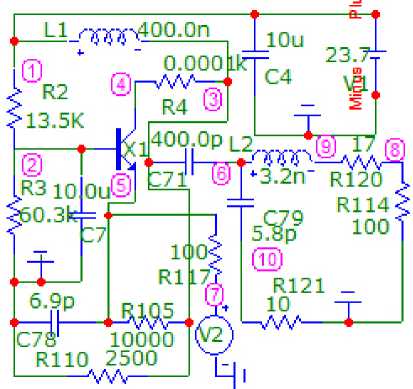
Рисунок 5. Принципиальная схема однокаскадного АФМ, соответствующая структурной схеме (рисунок 1, а ), в первом состоянии при

U = 23,7 В, исследуемая в системе MicroCap

а

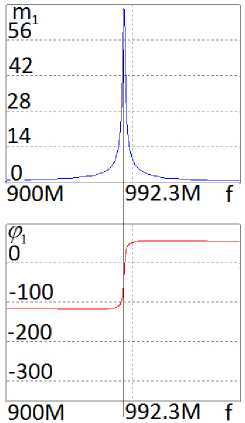
Рисунок 6. Частотные характеристики (АЧХ и ФЧХ) в первом ( а ) при U = 23,7 В и втором ( б ) при U = 21,4 В состояниях, полученные в системе MicroCap

б

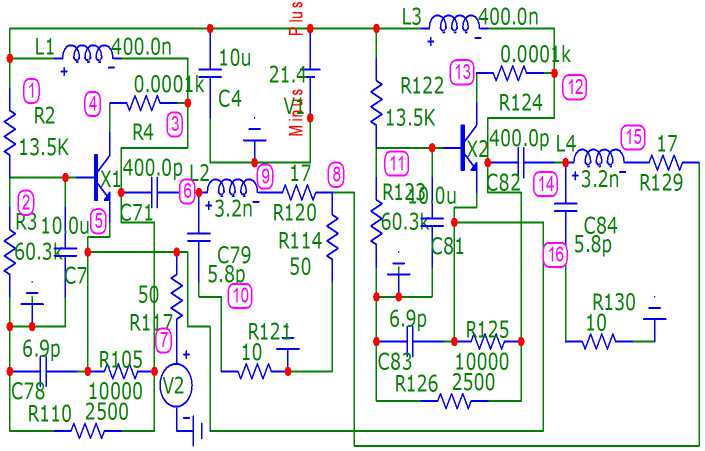
Рисунок 7. Принципиальная схема двухкаскадного АФМ, соответствующая структурной схеме (рисунок 1, а ), частотные характеристики которого идентичны соответствующим характеристикам однокаскадного АФМ (рисунок 5)

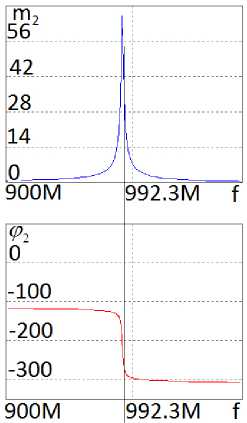
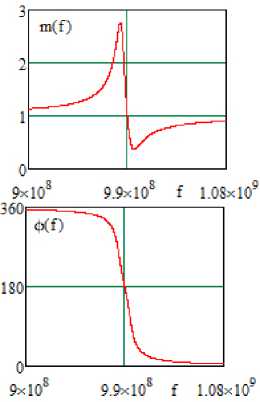
частотные характеристики принципиальной схемы АФМ (рисунки 5, 7) удовлетворительно совпадают с характеристиками эквивалентной схемы (рисунки 10, 11) АФМ в двух состояниях, полученными расчетным путем (рисунок 8, а ) и экспериментально (рисунок 12, а , б ). Средняя частота эквивалентной схемы f « 990 МГц (рисунки 10 и 11) незначительно отличается от средней частоты принципиальной схемы f « 992,2 МГц (рисунки 5, 7). На этой частоте теоретически и путем схемотехнического моделирования [5] реализован так называемый режим п -манипуляции выходного сигнала, при котором в двух состояниях отношение модулей передаточной функции m = 1, а разность фаз ф = 180 ° . Значения модулей передаточной функции АФМ в двух состояниях равны m 1 = m ₂ = 42 .

Сопротивления РЧ, ЦОС, нагрузки и источника сигнала принципиальных и эквивалентных схем АФМ полностью совпадают.

Для расчета модуляционных характеристик (зависимостей модуля и фазы передаточной функции АФМ от уровня управляющего сигнала (рисунок 6, б )) в рамках разработанного алгоритма использовались значения элементов матрицы проводимостей транзистора в двух рабочих состояниях, соответствующие эквивалентным схемам НЭ, показанным на рисунках 10 и 11.

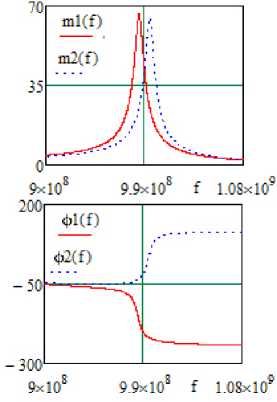
Зависимости модуля и фазы передаточной функции АФМ от непрерывного изменения уровня управляющего сигнала (модуляционные характеристики), полученные расчетным путем (рисунок 9, а ) и путем схемотехнического моделирования (рисунок 9, б ), значительно отличаются.

Это связано с тем, что разработанный в данной статье алгоритм позволяет обеспечить удовлетворительное совпадение расчетных и экспериментальных характеристик только в двух состояниях,

б

Рисунок 8. Теоретические частотные характеристики (АЧХ и ФЧХ в двух состояниях, одинаковые для однокаскадного (рисунок 5) и двухкаскадного (рисунок 7) АФМ) ( а ) и зависимости отношения модулей и разности фаз передаточной функции АФМ от частоты ( б ), полученные в системе MathCad

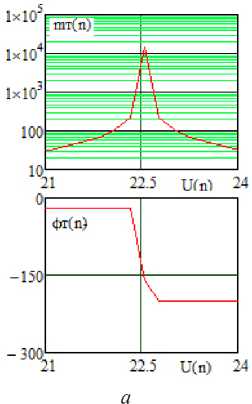
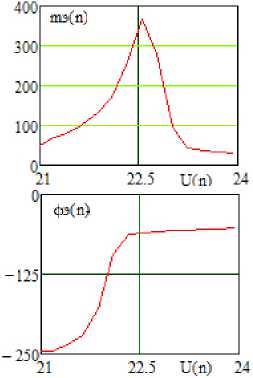
б

Рисунок 9. Теоретические зависимости модуля и фазы передаточной функции АФМ от уровня управляющего сигнала, полученные в системе MathCad ( а ), и экспериментальные ( б ) зависимости модуля и фазы передаточной функции АФМ от уровня управляющего сигнала, полученные в системе MicroCap

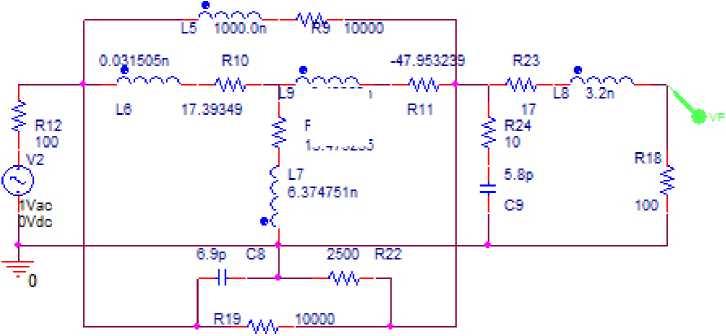
3.4965Эп

R13 13.475255

Рисунок 10. Эквивалентная схема однокаскадного АФМ (рисунок 4), соответствующая структурной схеме (рисунок 1, а ) в первом состоянии, исследуемая в системе OrCad

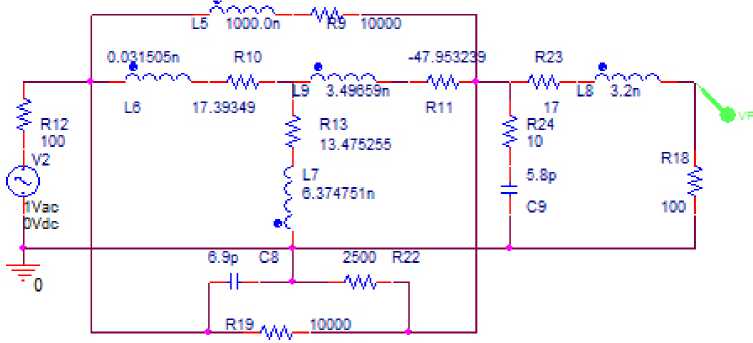
Рисунок 11. Эквивалентная схема однокаскадного АФМ (рисунок 3), соответствующая структурной схеме (рисунок 1, а ) в другом состоянии, полученная в системе OrCad

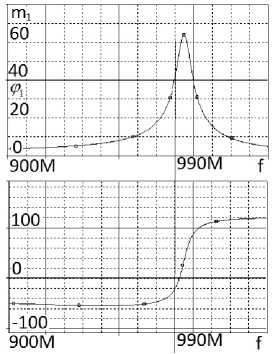
а

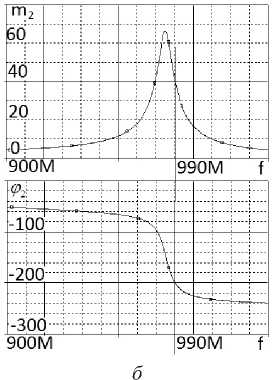
Рисунок 12. Частотные характеристики (АЧХ и ФЧХ) эквивалентных схем (рисунки 8, 9) однокаскадного АФМ (рисунок 4), полученные в системе OrCad в первом ( а ) и втором ( б ) состояниях

определяемых двумя уровнями управляющего сигнала.

Заключение

Таким образом, полученные математические модели КЧ-типа (1)–(6) могут быть использованы для технического проектирования амплитудно-фазовых модуляторов и манипуляторов с заданными частотными характеристиками. Возможность изменения величины сопротивления источника сигнала и нагрузки путем включения произвольного количества каскадов типа НЧ – РЧ значительно упрощает решение многих задач радиоэлектроники, например задач обеспечения однонаправленности распространения сигнала и независимости процессов, происходящих в предыдущем и последующем динамических звеньях систем автоматического регулирования [6–10].