Параметрический синтез амплитудно-фазовых модуляторов с заданным количеством одинаковых каскадов типа "нелинейная часть - резистивный четырехполюсник"

В работе [1] сформулирована задача и разработан алгоритм параметрического синтеза согласующих четырехполюсников различных типов (реактивных, резистивных, комплексных и смешанных) по критерию обеспечения заданных частотных характеристик многокаскадных амплитудно-фазовых модуляторов (АФМ). В частности, решена задача синтеза АФМ с использованием одинаковых каскадов типа «нелинейная часть (НЧ) – реактивный четырехполюсник».

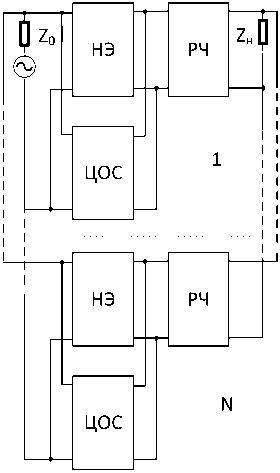
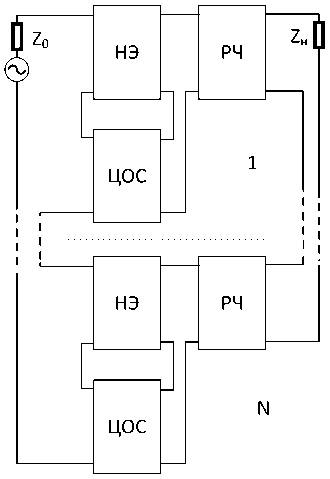
Цель данной работы состоит в изменении областей физической реализуемости заданных характеристик АФМ путем использования произвольного количества N одинаковых каскадов типа «НЧ – резистивный четырехполюсник (РЧ)» между источником сигнала с сопротивлением z 0 = ^r0 + jx 0 и нагрузкой z H = r + jX (рисунки 1, 2) и специального выбора параметров РЧ.

Каскады соединяются между собой с использованием того вида обратной связи, по которому соединены нелинейный элемент (НЭ) и цепь обратной связи (ЦОС) (параллельной или последовательной по току или напряжению).

Основные положения теории синтеза, которые использованы при получении результатов, изло- жены в работах [2–4]. Оптимизация параметров двухполюсников, не входящих в РЧ, осуществляется с помощью известных численных методов [5] по критерию обеспечения заданной рабочей полосы частот. Все обозначения неописанных величин и аббревиатур в данной статье соответствуют принятым в [1].

1.    Результаты параметрического синтеза

Здесь в качестве примера приводятся некоторые из решений, полученных для типовых схем РЧ при использовании параллельной по напряжению обратной связи (рисунок 1, а ). Если в качестве РЧ используется схема в виде двух обратных Г-образных соединений из четырех двухполюсников (рисунок 3), то формулы для определения зависимостей сопротивлений X 1 2 3 4 этих двухполюсников от частоты определяются следующим образом:

R1 = [(R4 - cr )(R2 + R3 ) - R4 (cr + arR2 ) -

- R 2 R 3 (ar + brR 4)]/              (1)

/[(ar + brR 4)(R 2 + R 3) + arR4 ];

R 2 =

- B 2 ± V B ₂ ² - 4 A 2 C 2 2 A ₂

где

а

б

Рисунок 1. Структурные схемы многокаскадных АФМ с параллельной по напряжению ( а ) и последовательной по току ( б ) цепями обратной связи,

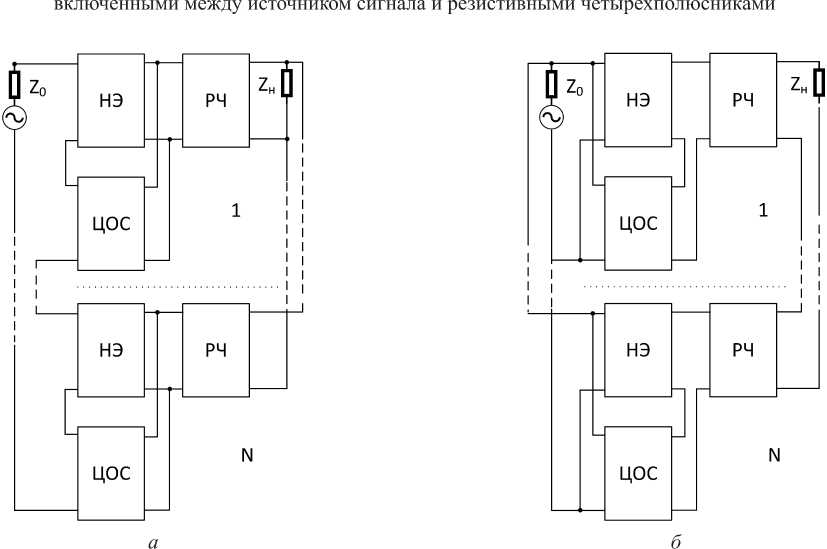
Рисунок 2. Структурные схемы многокаскадных АФМ с последовательной по напряжению ( а ) и параллельной по току ( б ) цепями обратной связи, включенными между источником сигнала и резистивными четырехполюсниками

A 2 = ( b x — a_rb x + a_xb_r ) R 4 + A ;

A ₀ = ( a_x + b_rc_x — b_xc_r ) R ₄ + a_rc_x — a_xc_r ;

B 2 = R 4 (2 R 3 + R 4 )( a x + b r C x — b_xc_r ) + B o ;

B o = 2( a r c x — a x c r )( R 3 + R 4 ) + 2 b x R 3 R 4 ;

C 2 = R 3 R 4 ( R 3 + R 4 )( a x + b r c_x — b x c r ) + C 0 ;

C 0 = ( a r c x — a x c r )( R 3 + R 4 ) ² + b x R 3 R 4 •

R i = [ ( R 4 — c )( R ₂ + R 3 ) — R ₄ ( c_r + aR ) — — R 2 R 3 ( a_r + b_rR 4 ) ]/ /[ ( a_r + b_rR 4 )( R 2 + R 3 ) + a_rR 4 ];

^R3 =

— В з±7 В 2

—

2 A ₃

4 A ₃ C ₃

,

где

^A 3 = ^bx^R 42 ^{+ (} a x ⁺ b r c x ^—

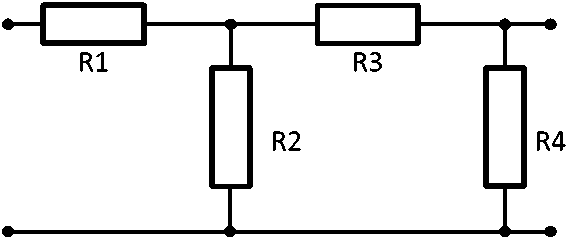
Рисунок 3. Пример синтезированного соединения двух обратных Г-образных звеньев

Х_п = а с —ас; 0 r x x r ^;

В з = R 4 (2 R ₂ + R 4 )( a_x + b_re_x - b_xc_r ) + В 0 ;

В 0 = 2( X о )( R 2 + R 4 ) + 2 b x R 2 R 4 ;

C 3 = ( X 0 )( R 2 + R 4 ) ² + C о ;

C ₀ = R ₂ ² R ₄ ² ( b_x - a_rb_x + a_xb_r ) + + R 2 R 4 ( R 2 + R 4 )( a x + b r C x - b_xe_r ).

R i = [ ( R 4 - C r )( R 2 + R 3 ) - R 4 ( C r + a r R 2 ) -- R 2 R 3 ( a r + b r R 4 ) ]/ /[ ( a r + b r R 4 )( R 2 + R 3 ) + a r R 4 ];

R 4 =

- В 4 ± В В 22 - 4 A 4 C 4

2 A 4

где

A 4 = ⁽ R 2 ^{+ R} 3 ⁾⁽ a x ⁺ b r c x ^- b x c r ) ⁺

^{+ ( b}x ^- a r b x ⁺ a x b r ) ^R 22 ⁺ A 0 ;

A = b x R 3 (2 R 2 + R 3 ) + X 0 ;

C 4 = ( X 0 )( R 2 + R 3 ) ² ;

В 4 = 2( X 0 )( R 2 + R 3 ) +

+ ( R 2 + R 3 ) ² ( a x + b r C x - b x C r );

R 2 = [(1 - b r R i ) R 3 R 4 - ( C r + a r R i )( R 3 + R 4 )]/ /[( a r + b r R 4 )( R i + R 3 ) + C r + R 4 ( a r - 1)];

R 3 =

- В ₃ ± 7 В ₃ ² - 4 A ₃ C ₃

2 A ₃

где

A 3 = ⁽ b x^Cr ^{- b}r^Cx - a x ) ^R 4 ^{- b}x^R 42 ^- X 0 ^;

В ₃ = ( b_xC_r - b_rC_x - a_x ) R 4 + 2( a_xC_r - a_rC_x ) R ₄ ;

C 3 = R 4 [ C 0 R i² + ( a x - b r C x + b x ^ r ) R i + C x - X 0 ];

C ₀ = a_rb_x - a_xb_r ;

R 2 = [(i - b r R i ) R 3 R 4 - ( C r + a r R i )( R 3 + R 4 )]/

/ [( a r + b r R 4 )( R i + R 3 ) + C r + R 4 ( a r - i)];

R 4 =

- В 4 ± В В 4 - 4 A 4 C 4

2 A ₄

где

A ₄ = ( a_rb_x - a_xb_r ) R^ +

^{+ ( a} _x ^{- b}r^C _x ^{+ b} _x ^Cr ) ^R _i ^{- b}_x^R3 ⁺ A o ^;

A ₀ = ( b_xC_r - b_rC_x - a_x ) R _i + C_x - a_rC_x + a_xC_r ; В ₄ = ( b_xC_r - b_rC_x - a_x ) R ₃ ² + 2( a_xC_r - a_rC_x ) R ₃ ;

C ₄ = ( a_xC_r - a_rC_x ) R ₃ ² .

R 3 = {[ R 4 - C r - R i ( a r + b r R 4 ) - a r R 4 ] R 2 - ^{- R} 4 ^{( C}r ^{+ a}r^Ri ^)} / /{( a r + b r R 4 )( R i + R 2 ) + C r - R 4 };

^R 4 ⁼

- В 4 ± В в 42 - 4 A 4 C 4

2 A 4

где

A 4 = ^{( R} i ^{+ R} 2 ⁾⁽ a x - ^br^Cx ^{+ b}x^Cr ) ⁺ A 0 ;

A 0 = C x - b x R 2² + ( a r b x - a x b r )( R i + R 2 ) ² ;

В 4 =- R 2² ( a x + b r C x - b x C r );

C ₄ = R ₂ ² ( a_xC_r - a_rC_x ).

• 2.    Математическое и схемотехническое моделирование амплитудно-фазовых модуляторов с одинаковыми каскадами типа НЧ – РЧ

На рисунках 4–11 для примера показаны принципиальные и эквивалентные схемы однокаскадного и двухкаскадного АФМ, соответствующие исследуемой структурной схеме с параллельной по напряжению связью, представленной на рисунке 1, а , а также их теоретические и экспериментальные характеристики. Использован транзистор типа BFQ17PH (рисунки 4, 6). Схема НЧ выполнена в виде параллельно соединенных транзистора и ЦОС (П-образного соединения трех элементов C 78 , R _i05 , R _ii0 ) на однокаскадной схеме (рисунок 4) и C 78 , R _W5 , R _1W , C ₈2 , R _W5 , R_U 0 на двухкаскадной схеме (рисунок 6). Нагрузка и сопротивление источника сигнала выполнены на элементах R ₁₁₄ и R ₁₁₇ соответственно. Схемы РЧ собраны в виде двух обратных Г-образных четырехполюсников на элементах R _i04 , R _ii5 , R _ii6 , ^R ii8 (рисУнок ⁴⁾, ^R i04 , ^R ii5 , ^R ii6 , ^R ii8 , ^R i22 , ^R i26 , R _i27 , R _i29 (рисунок 6), параметры которых определялись по формулам (1).

Эквивалентная схема нелинейного элемента выполнена в виде перекрытого Т-образного четырехполюсника на элементах R _i0 , L ₆ , R _i3 , L ₇ , R _ii , C ₉ , R 9 , L 5 (рисунок 9, i0). Параметры эквивалентной схемы НЭ выбраны из условия совпадения выходного сопротивления НЧ с выходным сопротивлением НЧ с использованием реального транзистора [3]. Схема НЧ реализована в виде

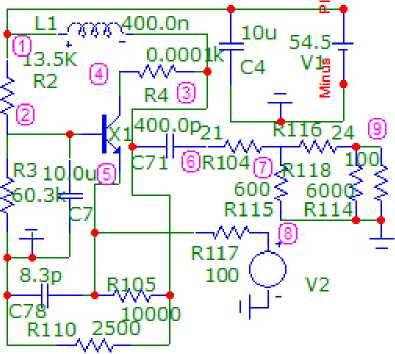
Рисунок 4. Принципиальная схема однокаскадного АФМ, соответствующая структурной схеме (рисунок 1, а ), в первом состоянии при U = 54,5 В и исследуемая в системе MicroCap

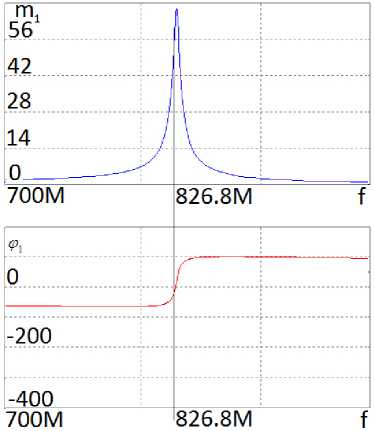
а

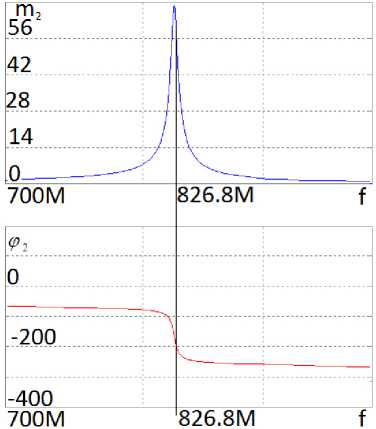
Рисунок 5. Частотные характеристики (АЧХ и ФЧХ) в первом ( а ) при U = 54,5 В и втором ( б ) при U = 44 В, полученные в системе MicroCap

параллельно соединенных эквивалентной схемы нелинейного элемента и цепи обратной связи из П-образного соединения трех элементов C8, R19, R22. Параметры ЦОС заданы произвольно. Схема РЧ собрана на основе двух обратных

Г-образных соединений четырех элементов R 20 ,

R R R

R 21 , R 23 , R

Частотные характеристики принципиальных схем, показанных на рисунках 4 (сопротивления источника сигнала и нагрузки равны 100 Ом) и 6 (сопротивления источника сигнала и нагрузки равны 50 Ом), идентичны. Это соответствует вы- водам, сделанным на основе анализа полученных выше выражений для передаточных функций исследуемых структурных схем (рисунок 1, а). Анализ также показывает, что экспериментальные (рисунок 5, а, б) частотные характеристики принципиальной схемы АФМ (рисунки 4, 6) удовлет- ворительно совпадают с характеристиками эквивалентной схемы (рисунки 8, 9) АФМ в двух состояниях, полученными расчетным путем (рисунок 7, а) и экспериментально (рисунок 11, а, б).

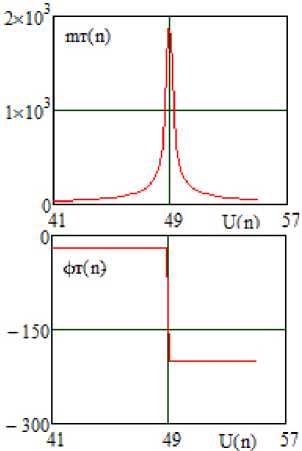
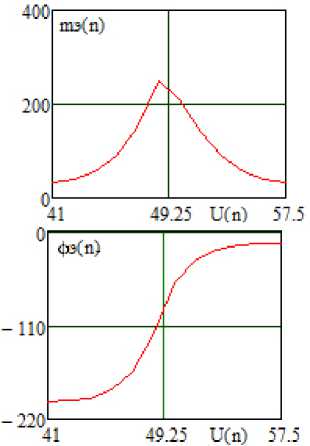
Зависимости модуля и фазы передаточной функции АФМ от непрерывного изменения уровня управляющего сигнала (модуляционные характеристики), полученные расчетным путем (рисунок 8, а ) и путем схемотехнического моделирования (рисунок 8, б ), значительно отличаются.

Это связано с тем, что разработанный в данной статье алгоритм позволяет обеспечить удовлетворительное совпадение расчетных и экспериментальных характеристик только в двух состояниях, определяемых двумя уровнями управляющего сигнала.

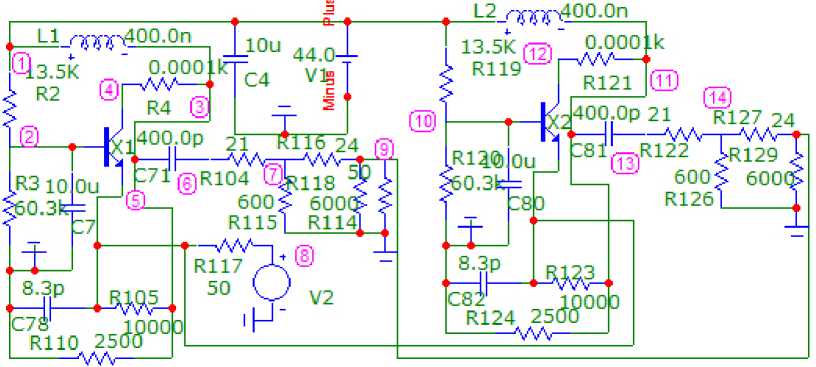
Рисунок 6. Принципиальная схема двухкаскадного АФМ, соответствующая структурной схеме (рисунок 1, а ), частотные характеристики которого идентичны соответствующим характеристикам однокаскадного АФМ (рисунок 4)

а

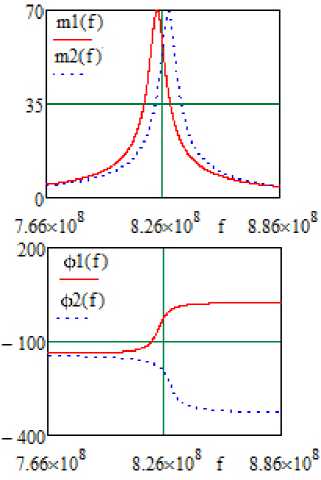
Рисунок 7. Теоретические частотные характеристики (АЧХ и ФЧХ в двух состояниях, одинаковые для однокаскадного (рисунок 4) и двухкаскадного (рисунок 6) АФМ) ( а ) и зависимости отношения модулей и разности фаз передаточной функции АФМ от частоты ( б ), полученные в системе MathCad

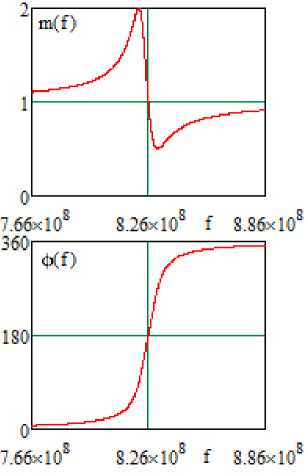
б

Средняя частота эквивалентной схемы f ® 826 МГц (рисунки 7, а и 11, а , б) незначительно отличается от средней частоты принципиальной схемы f ® 826,8 МГц (рисунок 5, а , б). На этой частоте теоретически и путем схемотехнического моделирования [6] реализован так называемый режим п -манипуляции выходного сигнала, при котором в двух состояниях отношение модулей передаточной функции m = 1, а разность фаз ф = 180 ° .

Значения модулей передаточной функции АФМ в двух состояниях равны m 1 = m ₂ = 56. Сопротивления РЧ, ЦОС, нагрузки и источника сигнала принципиальных и эквивалентных схем АФМ полностью совпадают.

Заключение

Таким образом, полученные математические модели РЧ-типа (1) могут быть использованы для технического проектирования амплитудно-фазовых модуляторов и манипуляторов с заданными частотными характеристиками. Возможность изменения величины эквивалентного сопротивления источника сигнала и нагрузки путем включения произвольного количества каскадов типа НЧ – РЧ значительно упрощает решение многих задач радиоэлектроники [7–11], например задач обеспечения однонаправленности распространения сигнала и независимости процессов, происходящих в предыдущем и последующем

б

Рисунок 8. Теоретические зависимости модуля и фазы передаточной функции АФМ от уровня управляющего сигнала, полученные в системе MathCad ( а ), и экспериментальные ( б ) зависимости модуля и фазы передаточной функции АФМ от уровня управляющего сигнала, полученные в системе MicroCap

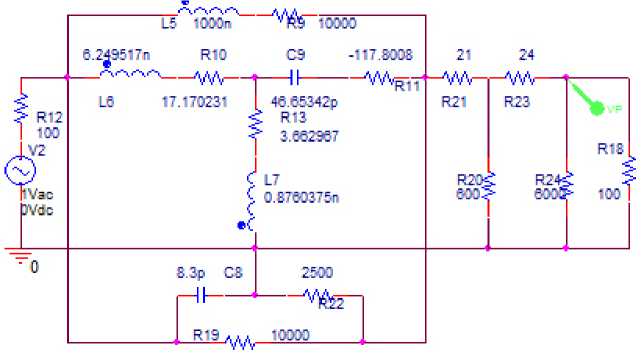
Рисунок 9. Эквивалентная схема однокаскадного АФМ (рисунок 4), соответствующая структурной схеме (рисунок 1, а ) в первом состоянии, исследуемая в системе OrCad

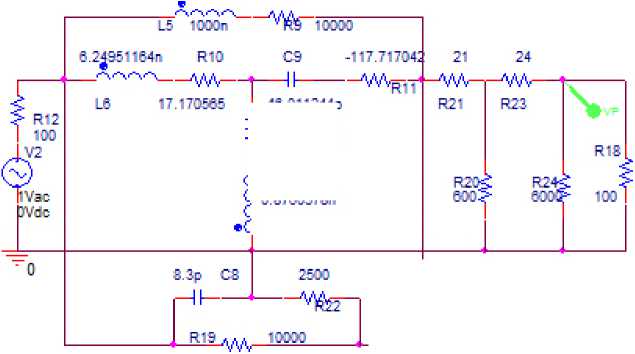
Рисунок 10. Эквивалентная схема однокаскадного АФМ (рисунок 3), соответствующая структурной схеме (рисунок 1, а ) в другом состоянии, полученная в системе OrCad

«.011244р R13

3.662634

Г 17

V O.B76337Sn

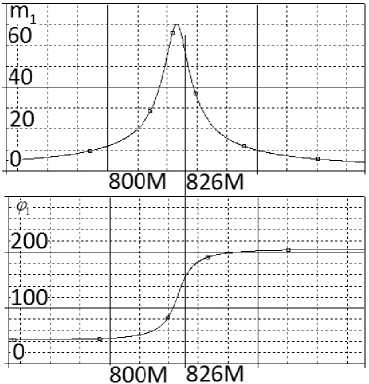
а

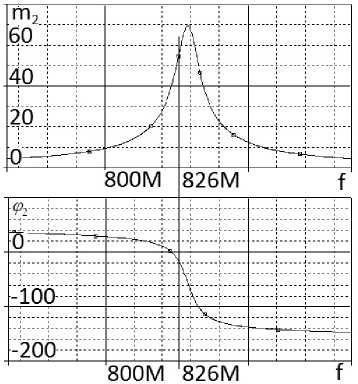
Рисунок 11. Частотные характеристики (АЧХ и ФЧХ) эквивалентных схем (рисунки 8, 9) однокаскадного АФМ (рисунок 3), полученные в системе OrCad в первом ( а ) и втором ( б ) состояниях

динамических звеньях систем автоматического регулирования.