Параметрический синтез радиоустройств с заданным количеством неодинаковых каскадов для вариантов включения реактивных четырехполюсников между источником сигнала и нелинейной частью

В работах [1‒3] предложены алгоритмы параметрического синтеза согласующих четырехполюсников (СЧ), оптимальных по критерию обеспечения заданных характеристик усилителей, генераторов, модуляторов и высокочастотных частей демодуляторов сигналов с угловой модуляцией. При этом предполагалось, что нелинейная часть (НЧ) состоит из нелинейного элемента (НЭ) и охватывающей его цепи обратной связи (ЦОС), параллельной по напряжению, последовательной по току, последовательной по напряжению, параллельной по току. Исследовались структурные схемы, состоящие из одного каскада типа СЧНЧ и НЧСЧ.

Цель данной работы состоит в увеличении произведения коэффициента усиления на рабочую полосу частот (площади усиления) усилителей и демодуляторов путем включения произвольного количества неодинаковых каскадов типа «реактивный четырехполюсник (РЧ)НЧ», включенных по той же схеме, что и НЭ и ЦОС, между сопротивлениями источника сигнала z о = r ₀ + jx о и нагрузки z_H = г_н + jx_H (рисунок 1, а - г ).

Для достижения этой цели делается попытка решить задачу параметрического синтеза, состоящую в определении минимального количества двухполюсников согласующих РЧ и значений их параметров, при которых обеспечиваются заданные зависимости модуля m и фазы ф передаточной функции Н усилителей и демодуляторов с произвольным количеством указанных каскадов от частоты в одном из режимов работы нелиней-

H = m (cos ф + j sin ф).           (1)

Согласующие РЧ п-го (n = 1,2...N) каскада характеризуются искомыми зависимостями элементов an,bn, cn, dn классической матрицы передачи от частоты.

В интересах составления исходных уравнений, удовлетворяющих (1), найдем передаточные функции для каждой структурной схемы. Для этого будем использовать известные правила применения матриц различных параметров для описания четырехполюсников и их соединений, а также условия нормировки общей матрицы передачи узла «РЧ‒НЧ» [1; 4]. Рассмотрим вариант структурной схемы с параллельной по напряжению обратной связью (рисунок 1, а).

Для этой схемы комплексные элементы классической матрицы передачи НЧ п -го каскада можно записать следующим образом:

a yn

• -^ -b =—-; У'уп             ;

y21n           y21n

⁽ y 11 n y 22 n    y 12 n y 21 n ). J     y 11 n

----------------------------; d yn =----- , ^y 21 n                      ^y 21 n

где

+ y OCn ;

, + y ocn

У11 n = y”n + yOCn; У12 n = уНЭп-

У 21 n = У 2³ln ⁺ У ocn ; У 22 n = У 2^n

‒ известные суммарные элементы матрицы проводимостей НЧ (НЭ и ЦОС).

Перемножим матрицы передачи РЧ и НЧ каждого каскада. Получим общие матрицы передачи и общие матрицы проводимостей отдельных ка-

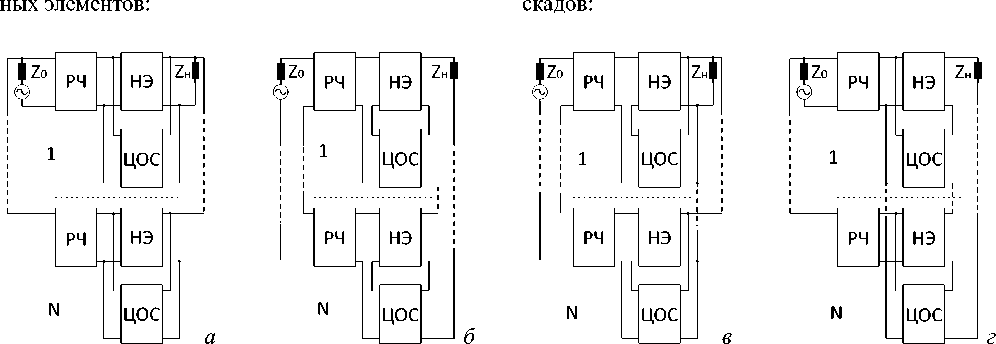
Рисунок 1. Структурные схемы многокаскадных радиоустройств с параллельной по напряжению ( а ), последовательной по току ( б ), последовательной по напряжению ( в ), параллельной по току ( г ) цепями обратной связи, включенными между РЧ и нагрузкой

Aкn

A n

n

B n

D n

кn

11 n      12 n

21 n     22 n

где

Ai = aay + jbcy; Bi = aby + jbdy;

A = [ Yi”Y£z 0 Zh + (1 + Yi oi cz 0) X X (1 - Y-zH)]by + ayZH (1 + YiOcz0 )• C0 = z0 [ayZH + by (1 - Y-Zh )];

Ci = Cyd + ayjc; Di = b jc + dyd; Yin = Dn;

Bn

12 n

-(AnDn - BnCn) ,

B n

⁷ = — 21 n B n

^^^^^^B

• Y =nL

’ ^{22 n} B ■ n

Общая матрица проводимостей всех N каскадов находится путем суммирования матриц проводимостей отдельных каскадов. Из сумм элементов матриц проводимостей выделим отдельно элементы матрицы проводимостей п -го каскадов и выразим их через элементы матрицы передачи. Остальные каскады можно рассматривать как цепи обратной связи. Следовательно, элементы общей матрицы передачи многокаскадной схемы

можно записать в следующем виде:

A ym

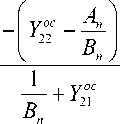
• B ym

—+ Y

B ² n

D n + y o _B 11

n

ym

где

— + Y oc

_B 21 n

-

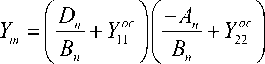
- ( A n D n - B n C n )

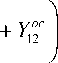
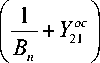
N

Z Y i2m ;

m = 1, m * n

N

oc

N

E K * к ^oc

11 m ^;   12

m = 1, m * n

oc

N

oc

21 m ^;    22

m = 1, m * n

Z Y 22 m ;

m = 1, m * n

Y O ^c , Y 2 ^c , Y Oc , Y jj - известные зависимости суммарных элементов матрицы проводимостей всех каскадов (кроме п -го) от частоты.

Тогда передаточную функцию для структурной схемы с параллельной по напряжению ЦОС, показанной на рисунке 1, а , можно записать в следующем виде:

H =

=            Zh [YOc (aby + jbd) + 1]              (5)

aA0 + jbB0 + jcC0 + dD0 + (ad + bc) E0 + H0

где

B 0 = [ Y i № 0 Z h + (i + Y i oi c z 0 ) x

x (i - Y2Z )]dy + cz (i + YiOcz0);

D0 = z0 [c z. + dy (i - Y22ZH)]; H0 = Yiz0z.;

E0 =-Y"=z0Zh(aydy -bycy).

Подставим (5) в (1). Получим комплексное

уравнение, решение которого приводит к взаимосвязи элементов классической матрицы передачи РЧ, оптимальной по критерию (1):

an

(-Ci cn + B) bn + Di dn + C-cn + C C1 dn + D

где

B = JdyyOX - jB0M = br + jb*;

C = Zh - H0 M = cT + jc*;

Ci = E0 M = ci r + jci x;

C2 =- jC0 M = c2 r + jc2 x;

D = A0M - byyOczH = dr + jd*;

Di =- D0 M = di r + jdi *;

M = m (cos ф + j sin ф).

При использовании последовательной по току ЦОС (рисунок 1, б ) передаточную функцию можно представить следующим образом:

H=

Zh [ZOc (jayc + cyd) + i]               (7)

aA0 + jbB0 + jcC0 + dD0 + (ad + bc) E0 + H 0

где

A0 = by + ay ( Zh - ZOc); B0 = dy + cy (z. - ZOc);

C0 = (z0 + ZOc)[by + ay (Zh - ZOc)] + ayZOZ^;

D0 = (z0 + Z00)[dy + cy(Zh - ZOO)] + cyZiO2cZOc;

E0 =-ZOc (aydy - bycy) ;H0 = ZOc;

c

^Z 11

N

Z Z ii m

c

Z i2 =

m = i, m * n

N

c

21             21m m=i, m * n

c

Z 22 =

N

Z Z i2 m ;

m = i, m * n

N

Z Z 22 m ;

m = i, m * n

Z c c c c

11 , Z i- , z -1 , z oo - известные зависимости суммарных элементов матрицы сопротивлений всех каскадов (кроме п -го) от частоты.

Взаимосвязь между элементами классической матрицы передачи ССЧ, оптимальной по критерию (1), можно также представить в форме (6), но при следующих уточнениях:

B = - jB 0 M = b r + jb x ;

C = Z h - H о M = c r + jc_x ;

C i = E о M = c r + c x ;

^C 2 = jayzZ 21 - ^jC 0 ^M = ^C 2 r ⁺ jc 2 x ^;

D = A M = d r + jd x ;

D i = C y Z ^ ZЦ - D о M = d i r + jd i x .      (8)

При использовании последовательной по напряжению ЦОС (рисунок 1, в ):

H =

=           Z h [ HЦ ( jb_yc + d y d ) + i]             (9)

aA + jbB ₀ + jcC ₀ + dD ₀ + ( ad + bc ) E ₀ + H ₀

где

A = a y Z H + b y (i - H O z );

B 0 = C y Z H + d y (i - H i z );

E 0 = H Ц z н ( a y d y - b y C y );

h 0 = h ii z н ;

C 0 = ( z 0 + H ii )[ a y Z H +

+ b y (i - H OC Z h )] + b y H -h 2 ⁰C Z h ;

D 0 = ( z 0 + H iC )[ C y Z H +

+ d y (i - h OC Z h )] + d y HЦн OC Z h ;

H ii = / H ii m ; H ii = / H i2 m ;

m = i, m * n                     m = i, m * n

H iC = / H 2i m ; H ii = / H 22 m ; m = i, m * n                     m = i, m * n

H “, H ii , H iC , H 2Ц - известные зависимости суммарных элементов смешанной матрицы H всех каскадов (кроме п -го) от частоты.

Коэффициенты для взаимосвязи (6) между элементами классической матрицы передачи ССЧ, оптимальной по критерию (1):

B = - jB ₀ M = b_r + jb x ;

C = Z h - H 0 M = C r + jc_x ;

C i = E 0 ^M = ^ci r + c x ;

c 2 = jb_yz„H iC - jC 0 M = C 2 r + jc 2 x ;

D = A y M = d r + jd x ;

D i = d y Z H H OC - D 0 M = d i r + jd i x .     (i0)

При использовании параллельной по току обратной связи (рисунок , г ):

H =

=             Z h [ F jj ( a y a + ji y b ) + i ]             (i i)

aA ₀ + jbB ₀ + jcC ₀ + dD ₀ + ( ad + bc ) E ₀ + H ₀

где

C 0 = [ b y - a y ( F 2 ^o 2 ^c - Z h )] z 0 ;

D 0 = [ d y - C y ( F 22 - Z h )] z 0 ;

E 0 = F i Z 0 ( a y d y - b y C y );

A 0 = (i + f o ^cz 0 )[ b y -

- a y ( F ii - Z h )] + a y F i ⁰ 2 ^CF ii ^Cz 0 ;

B 0 = (i + F ii z 0 )[ d y -

- C y ( F i - Z h )] + C y F^F ^ z 0 ;

H 0 = F i2 ^C Z 0 ;

c       ^N               c       ^N

¹ ii         /a ii m ; ¹ i2         / , ¹ i2 m ;

m=i, m * n                   m=i, m * n c      N              c      N

¹ 2 i       T ¹ 2 i m ; ¹ 22 T ¹ 22 m ;

m = i, m * n                   m = i, m * n

"Г-ОС "Г-ОС "Г-ОС "Г-ОС ____________ _______________ _____

F ii , F i2 , F 21 , F 22 - известные зависимости суммарных элементов смешанной матрицы F всех каскадов (кроме п -го) от частоты.

Коэффициенты для взаимосвязи (6) для этого варианта:

B = ji y Z H F i - jB 0 M = b r + jb x ;

C = Z h - H 0 M = C r + jc_x ;

C i = E 0 ^M = c r + ^jc i x ;

C 2 =- jC 0 M = c 2 r + jc 2 x ;

D = A 0 M - a y Z H F™ = d r + jd_x ;

D _i =- D ₀ M = d _{i r} + jd _{i x} .         (12)

Для отыскания выражений для определения параметров типовых схем РЧ надо взять известные формулы для элементов a n , b_n , c_n , d_n [ i; 4], зависящих от сопротивлений или проводимостей двухполюсников, а также коэффициенты B , C , C _i , C ₂ , D , D _i для (6) с выбранным типом обратной связи. Затем надо разделить между собой действительную и мнимую части полученного комплексного уравнения и решить сформированную таким образом систему двух алгебраических действительных уравнений относительно сопротивлений или проводимостей двух двухполюсников выбранной схемы РЧ. В результате получаются ограничения в виде зависимости сопротивлений двух двухполюсников РЧ п -го каскада от частоты, оптимальные по критерию ( ). Задача реализации этих частотных характеристик с помощью квазиоптимальных двухполюсников в ограниченной полосе частот решена в работе [ ]. Параметры остальных двухполюсников РЧ и ЦОС п -го каскада, свободных от указанных ограничений, а также параметры двухполюсников РЧ и

ЦОС всех остальных каскадов выбираются из условия обеспечения других критериев, например из условия обеспечения заданной формы АЧХ и ФЧХ [1]. Для этого могут быть использованы известные численные методы оптимизации [5]. При этом скорость оптимизации увеличивается в сотни раз по сравнению со скоростью оптимизации с помощью только численных методов. Это связано с тем, что при использовании получаемых таким образом ограничений на каждом шаге оптимизации, включая первый, на заданном количестве частот обеспечивается совпадение реальных значений модуля и фазы передаточной функции с заданными (1).

Результаты параметрического синтеза

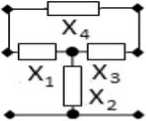
Рисунок 2. Пример синтезированного РЧ для устройств с заданным количеством неодинаковых каскадов типа РЧ‒НЧ

- X 4 ( d x - b x X 3 )( X 3 + X 4 )].

X 1 = {[ C 2 r - X 2 ( C r - C 1 r - d r + d 1 r )] X X ( X 3 + X 4 ) - X 3 X 4 ( d 1 r + b r X 2 )} / ^{/{( C}r ^{- C} 1 r ^- d r ^{+ d} 1 r ^{+ b}r^X 4 ) ^X

^{X (} X 2 + X ₃ ) ^{- C} 2 r ^- X 4 d r ^};

Здесь в качестве примера приводятся некоторые из решений, полученных для типовых схем РЧ и структурной схемы с параллельной по напряжению ЦОС (рисунок 1, а ). Пусть в качестве РЧ применяется перекрытое Т-образное соединение двухполюсников X 1 2 3 4 (рисунок 2). Тогда зависимости сопротивлений двухполюсников от частоты для шести возможных сочетаний по два определяются следующим образом:

X 1 = {[ c 2 r - X 2 ( C r - c r - d r + d 1 r )] x

X ( X 3 + X 4 ) - X 3 X 4 ( d 1 r + b r X 2 )} /

/( C r - c r - d r + d 1 r + b r X 4 )( X 2 + X 3 ) -    (13)

^{- C} 2 _r - ^X ₄ ^dr ^;

где

_ - B 3 ± 7 B 3² - 4 A 3 C 3

X ³ =        2 A 3

A 3 = ( b x d 1 r - b r d 1 x ) X 4² + ( C 2 r - d 1 r X 4 ) X

^{X ( C} 1 x ^{- C}x ^{+ d}x ) ^{- ( C} 2 x ^{- d} 1 x^X 4 ^{)( C} 1 r ^{- C}r ^{+ d}r ) ⁺ + c 2 x ( d 1 r + b r X 4 ) - c 2 r ( d 1 x + b x X 4 );

B 3 = [( b x d 1 r - b r d 1 x )2 X 2 + b r C 2 x - b x C 2 r ] X 2 + + X 4 ( C r - C 1 r )[( b x X 4 - d 1 x - d x ) X 2 + c 2 x ] - ^{- X} 4 ^{( C}x ^{- C} 1 x ^{)[( b}r^X 4 - ^d 1 r - ^dr ) ^X 2 ^{+ C} 2 r ^{] + B} 0 ^;

B 0 = X 4 (2 X 2 + X 4 )( d r d 1 x -- d x d 1 r ) + 2 X 4 ( C 2 r d x - C 2 x d r );

X = - B 2 ± Bb 2 - 4 A 2 C 2

²            2 A ₂

где

A 2 = ^[ b x ⁽ c r - ^C 1 r - d r ^{+ d} 1 r ) -

• ^-    b r ^{( C}x - ^C 1 x - ^dx ^{+ d} 1 x ^{)] X} 4 ;

B 2 = [( b x d 1 r - b r d 1 x )2 X 3 + b r C 2 x - b x C 2 r ] X 4 + + X 4 (2 X 3 + X 4 )( d r d 1 x - d x d 1 r ) +

+ X 4 ( C x - C i x )[ d r ( X 3 + X 4 ) +

+ X 3 ( d 1 r - b_TX 4 )] - B 0 ;

B 0 = X 4 ( C r - c r )[ d x ( X 3 + X 4 ) +

+ X 3 ( d 1 x - b x X 4 )];

C 3 = { c 2 r d x - c 2 x d r - X 2 [( d x - b x X 2 ) x

^{X ( C}r ^{- C} 1 r ^{+ d} 1 r ) ^{- ( d}r ^{- b}r^X 2 ^{)( C}x ^{- C} 1 x ^{+ d} 1 x ) ^- - b r C 2 x + b x C 2 r ] + X 22 ( b r d x - b x d r )} X 42 .

X 1 = {[ C 2 r - X 2 ( C r - C 1 r - d r + d 1 r )]( X 3 + X 4 ) -

- X 3 X 4 ( d 1 r + b_TX 2 )}/

^/{( c r ^{- C} 1 r ^{- d}r ⁺ d 1 r ^{+ b}r^X 4 ) ^X

^{X ( X} 2 + ^X 3 ) ^{- C} 2 r ^{- X} 4 ^dr ^};

X 4 =

- B ₄ ± Bb ₄ ² - 4 A ₄ C ₄

2 A ₄

C 2 = [ d 1 r ( b x X 3 - d x ) -

• -    d 1 x ( b r X 3 - d r )] X 3 X 4² + C 01 ;

C 01 = C 2 x [ X 3² d 1 r - X 4 ( d r - b r X 3 )( X 3 + X 4 )] -

• -    [ C 2 x ( X 3 + X 4 ) - d 1 x X 3 X 4 ] X

X X 3 ( C 1 r - C r + d r ) + C 02 ;

C 02 = [ C 2 r ( X 3 + X 4 ) - d 1 r X 3 X 4 ] X 3 X

^{X ( C} 1 x ^{- C}x ^{+ d}x ) ^{- C} 2 r ^{[ X} 32 ^d 1 x ^-

где

^A 4 = ^{[ b}r^C 2 x ^{- b}x^C 2 r ^{- X} 3 ^{( b}r^d 1 x ^{- b}x^d 1 r ) ⁺

+ b x X 2 ( C r - C 1 r + d 1 r ) - b r X 2 ( C x - C 1 x + d 1 x )] X x ( X ₂ + X ₃ ) + X 2 ( b_rd_x - b_xd_r ) + A 0 ;

A 0 = ^{[ d}r ^{( C}x ^{- C} 1 x ^{+ d} 1 x ) ^{- d}x ^{( C}r ^{- C} 1 r ^{+ d} 1 r ^{)] X} 2 ^{+ + X} 3 ^{( d}r^d 1 x - ^dx^d 1 r ) ^{+ C} 2 r^dx - ^C 2 x^dr ;

^B 4 = ^{{ B} 0 ^{- [ C} 2 x - ^d 1 x ^{( X} 2 ^{+ X} 3 ^{)]( C} 1 r - ^Cr ^{+ d}r ) -- ^C 2 x ^{( d}r - ^br^X 3 ) ^{+ C} 2 r ^{( d}x - ^bx^X 3 ) - ^{- X} 2 ^{[ d}x ^{( C}r - ^C 1 r ^{+ d} 1 r ) - ^dr ^{( C}x - ^C 1 x ^{+ d} 1 x ^{)]} X} 3 ;

B 0 = ^[ c 2 r - d 1 r ( X 2 + X 3 ^)]( c l x - c x + d x ) ;

^C 4 = ^[ c 2 x ⁽ c r - c l r - d r + ^d 1 r ) -- c 2 r ⁽ c x - c l x - ^dx + ^d 1 x ^{)] X} 32 •

X 2 = {( X 1 + X 3 + X 4 ) c 2 r -

- X 4 [ X 3 ( d 1 r + b r X 1 ) - d r X 1 ] - ^- X J X 3 ⁽ c r ^- c 1 r ^- d r + d 1 r ^)}/

/{( X 1 + X 3 ) X 4 b r + ( X 1 + X 3 + X 4 ) X X ⁽ c r ^- c r ^- d r ⁺ d 1 r ^)} ;

- B ₃ ± V B ₃ ² - 4 A 3 C ₃

X 3 =

2 A ₃

,

где

A 3 = ( b x d 1 r - b r d 1 x ) X 42 + ( c 2 r - d 1 r X 4 ) X

^{X (} c 1 x ^- c x ⁺ d x ) ^{- (} c 2 x ^- d 1 x^X 4 ⁾⁽ c 1 r ^- c r ⁺ d r ) ⁺ + c 2 x ( d 1 r + b r X 4 ) - c 2 r ( d 1 x + b x X 4 );

B 3 = c 2 x [ b r ( X 4 + 2 X 1 X 4 ) +

+ 2( X 1 + X 4 )( c r - c r + d 1 r )] -

• -    c 2 r [ b x ( X 4 + 2 X 1 X 4 ) + 2( X 1 + X 4 ) X

^{X (} c x ^{- c} 1 x ^{+ d} 1 x ^)] -

• -    d x [ d 1 r X 42 - c 2 r 2( X 1 + X 4 )] + B 0 ;

B 0 = d r [ d 1 x X 42 - c 2 x 2( X 1 + X 4 )] -

• ^{-    X} 4 ⁽ c x ^{- c} 1 x ^{)[ X} 1 ^{( d}r ^- b r^X 4 ) ^-

• -    d 1 r ( X 1 + X 4 )] + X 4 ( c r - c r ) X

X [ X 1 ( d x - b x X 4 ) - d 1 x ( X 1 + X 4 )];

C 3 = {[ c 2 x ( X 1 + X 4 ) + d x X 1 X 4 ]( c r - c r + d 1 r ) - ^{- [ c} 2 r ^{( X} 1 ^{+ X} 4 ) ^{+ d}r^X 1 ^X 4 ^]( c x ^{- c} 1 x ^{+ d} 1 x ) ⁺ + X 1 X 4 ( b r c 2 x - b x c 2 r )}( X 1 + X 4 ) + C 0 ;

C 0 = X 1² X 42 ( b r d x - b x d r ) +

+ ( c 2 r d x - c 2 x d r )( X 1 + X 4 ) ² •

X 2 = {( X 1 + X 3 + X 4 ) c 2 r -

- X 4 [ X 3 ( d 1 r + b r X 1 ) - d r X 1 ] -

^{- X} 1 ^X 3 ^{( c}r - ^c 1 r - ^dr ^{+ d} 1 r ^)}/

/{( X 1 + X 3 ) X 4 b r + ( X 1 + X 3 + X 4 ) X

^{X (} c r ^{- c} 1 r ^- d r + ^d 1 r ^)} ;

X 4 =

- B 4 ± BB 42 - 4 A 4 C 4 2 A ₄

где

A 4 = A 0 - ( X 1 - X 3 )( d r d 1 x - d x d 1 r ) -

- ⁽ c x ^{- c} 1 x ^{)[( d}r ^{- b}r^X 3 ) ^X 1 ^{+ c} 2 r ^{- d} 1 r^X 3 ^{] +} + ( c r - c 1 r )[( d x - b x X 3 ) X 1 + c 2 x - d 1 x X 3 ];

A , = ( b x d 1 r - b r d 1 x ) X 3² + X ² ( b r d x - b x d r ) - ^{- c} 2 r ^{[ d} 1 x ^{- d}x ^{+ b}x ^{( X} 1 ^{+ X} 3 ^{)] +}

+ c 2 x [ d 1 r - d r + b r ( X 1 + X 3 )];

B 4 = B 0 ^{+ [( d} 1 r^X 3 - ^dr^X 1 - ² c 2 r ⁾⁽ c x - ^c 1 x ) ⁺

^{+ (} c r ^{- c} 1 r ^{)( 2 c} 2 x ^{+ d}x^X 1 ^{- d} 1 x^X 3 ) ^-

- 2 c 2 x ( d r - d 1 r ) + 2 c 2 r ( d x - d 1 x )] X

X ( X 1 + X 3 ) - ( X ² - X 32 )( d r d 1 x - d x d 1 r );

B 0 = ( b r c 2 x - b x c 2 r )( X 1 + X 3 ) ² ;

^C 4 = ^[ c 2 x ⁽ c r - c 1 r - ^dr ^{+ d} 1 r ) -- c 2 r ⁽ c x - ^c 1 x - ^dx ^{+ d} 1 x ^{)]( X} 1 ^{+ X} 3 ⁾² •

X 3 = {[ c 2 r - X 2 ( c r - c 1 r - d r + d 1 r )]( X 1 + X 4 ) +

+ X 1 X 4 ( d r - b_TX 2 )} / {( c r - c 1 r - d r + d 1 r +

+ bX 4 )( X 1 + X 2 ) + d 1 r X 4 - c 2 r };

X 4 =

- B 4 ± V B 42 - 4 A 4 C 4 2 A 4

где

A 4 = {[ c 2 x + X 2 ( c 1 x - c x + d x ) + d x X 1 ] b r -- b x ( c 2 r + d r X 1 )}( X 1 + X 2 ) +

+ d _{1 r} ( b_xX ₂ ² + c _{2 x} + d_xX ₁ ) -

• -    d 1 x ( b r X 22 + c 2 r + d r X 1 ) + A ,;

• A , = X 2 { d 1 r ( c 1 x - c x + d x ) -

• -    ( c 1 r - c r + d r )[ d 1 x + b x ( X 1 + X 2 )]};

B 4 = B 0 + 2( c 2 x d 1 r - c 2 r d 1 x ) X 1 -

^{- ( c}x ^{- c} 1 x ) ^X 1 ^{[( d}r ^{( X} 1 ^{+ X} 2 ) ^{+ c} 2 r ^{+ d} 1 r^X 2 ^{] -}

• -    ( X ² + 2 X 1 X 2 )( d r d 1 x - d x d 1 r ) +

+ X ² ( b r c 2 x - b x c 2 r );

B 0 = ^X 1^{[( d}x ^{( X} 1 ^{+ X} 2 ) ⁺ c 2 x ^{+ d} 1 x^X 2 ^]( c r - ^c 1 r ^);

^C 4 = ^[ c 2 x ⁽ c r - c 1 r - ^dr ^{+ d} 1 r ) -

- c 2 r ⁽ c x - ^c 1 x - ^dx ^{+ d} 1 x ^{)] X} 12 •

Математическое и схемотехническое моделирование усилителей

На рисунках 3, 4 в качестве примера показаны эквивалентная и принципиальная схемы двухкаскадного усилителя, соответствующего структурной схеме рисунка 1, а при N = 2, и их характеристики. Использован транзистор типа BFQ17PH (рисунок3, а ).

Схема НЧ выполнена в виде параллельно соединенных транзистора и ЦОС в виде П-образного соединения трех элементов C 76 , R ₁₁₂ , R ₁₁₃ и C ₈₁ , R ₁₁₉ , R ₁₂₀ • Нагрузка и сопротивление источника сигнала выполнены на элементах R ₁₀₀ и R ₁₀₇ соответственно. Схемы РЧ собраны в виде Т-образного четырехполюсника на элементах L 6 , C 70 , L ₇ и L 9 , C ₈₀ , L ₁₀ , параметры двух из которых определялись по формулам (13) при X ₄ = да .

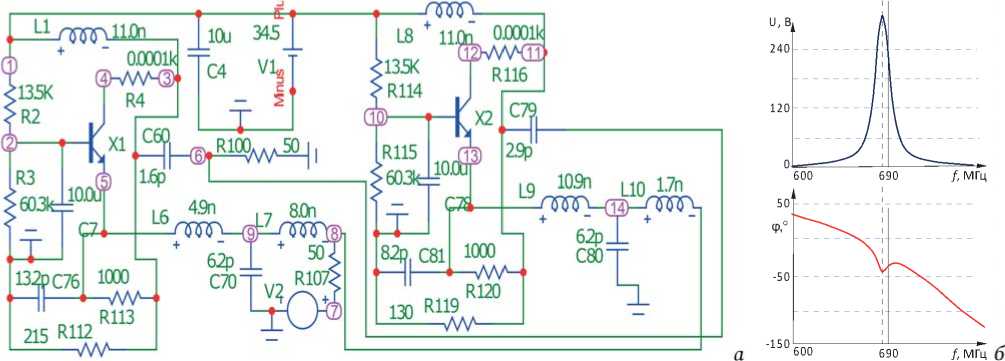
Рисунок 3. Принципиальная схема широкополосного усилителя ( а ), соответствующая первой структурной схеме (рисунок 1, а ), АЧХ- и ФЧХ-усилителя, полученные в системе MiсroCap ( б )

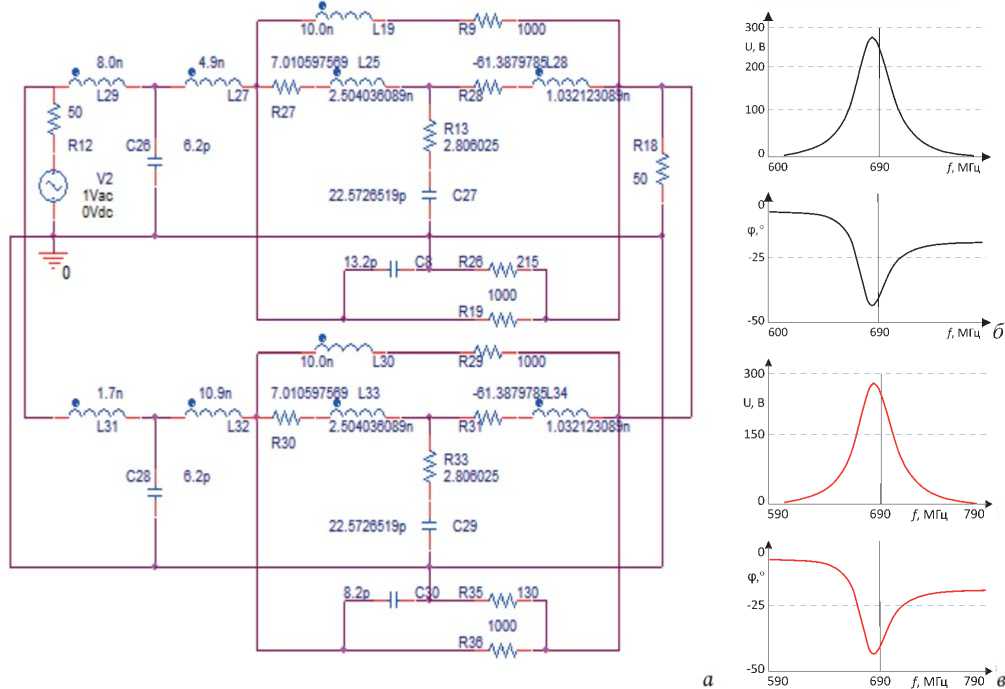
Рисунок 4. Эквивалентная схема ( а ) двухкаскадного усилителя (рисунок 4, а ), соответствующего первой структурной схеме (рисунок 1, а ), и ее АЧХ и ФЧХ, полученные в системе ОrCad ( б ) и в системе MathCad ( в )

Значения параметров третьего свободного двухполюсника, двух ЦОС и РЧ второго каскада опре- делялись численно.

Эквивалентные схемы НЭ выполнены в виде перекрытых Т-образных звеньев на элементах

R 27 , L 25 , R 13 , C 27 , R 28 , L 28 , R 9 , L 19 И R 30 , L 33 , R 33 , C 29 ,

R31, L34, R29, L30 (рисунок 4, а). Одинаковые значения параметров обоих эквивалентных схем НЭ выбраны из условия совпадения значений входного сопротивления НЧ этих схем на заданной частоте со значениями входного сопротивления НЧ при использовании реального транзистора [1].

Схемы НЧ реализованы в виде параллельно соединенных эквивалентной схемы нелинейного элемента и цепи обратной связи из П-образного соединения трех элементов C 8 , R 19 , R 26 и C ₃₀ , R 35 , R 36 . Схемы РЧ построены

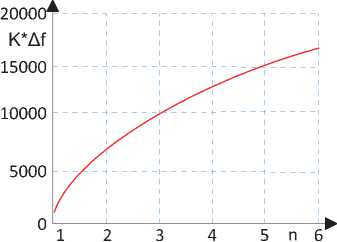
Рисунок 5. Зависимость произведения коэффициента усиления на полосу частот от изменения числа каскадов

на основе Т-образного соединения трех элемен- тов L29 , C26 , L27

и L 31 , C 28 , L 32 •

Заключение

Анализ полученных частотных характеристик показывает, что экспериментальные (рисунок 3, б ) характеристики принципиальной схемы (рисунок 3, а ) удовлетворительно совпадают с расчетными (рисунок 4, в ) и экспериментальными (рисунки 3, б и 4, б ) характеристиками эквивалентной схемы (рисунок 4, а ). Средняя частота рабочей полосы частот принципиальной схемы (рисунок 3, б ) совпадает со средней частотой эквивалентной схемы f ≈ 690 МГц (рисунки 4, б и в ). Площадь усиления составляет около 6200 МГц. Это примерно в 8‒10 раз больше площади усиления однокаскадного усилителя.

На рисунке 5 показана зависимость произведения коэффициента усиления на полосу частот от изменения числа каскадов с оптимизированными параметрами.

Для построения зависимости использованы значения коэффициента усиления и полосы частот, усредненные по десяти измерениям. Произведение коэффициента усиления на полосу частот с ростом числа каскадов увеличивается и асимптотически стремится к определенному пределу, примерно равному при шести каскадах K ∗∆ f ≈ 17000 МГц (рисунок 5). Дальнейшее увеличение числа каскадов нецелесообразно, поскольку приводит к усложнению схемы, a K ∗∆ f практически не возрастает.

Таким образом, полученные математические модели РЧ могут быть использованы для техни- ческого проектирования различных многокаскадных усилителей и демодуляторов в интересах реализации заданных частотных характеристик.