Параметрический синтез систем технического зрения в модифицированных дескриптивных алгебрах изображений

области. Материалы статьи описывают технологию разработки адаптивных систем технического зрения с привлечением математического аппарата модифицированных дескриптивных алгебр изображений и генетических алгоритмов для задач оптимизации.

Разработка функции СТЗ для измерения площади объектов

Например, рассмотрим изображение из шести монет с различными достоинствами, расположенных раздельно на плоскости под «правильным» освещением. В среде MATLAB были разработаны две программы, одна из которых реализует функцию вычисления количества объектов на изображении для последующего распознавания их достоинств. Вторая программа вычисляет на основании результата первой программы реальное число объектов на изображении, используя априорную информацию об этом количестве.

Подобный подход к созданию самообучающихся и адаптивных систем широко практикуется. Например, в работе [3] применяется нейронный слой Кохонена для понижения градации изображения географической карты. Здесь нейронная сеть в ходе самообучения группирует пиксели изображения по их цвету. Применение такого подхода предполагает изначальное задание числа нейронов равным числу цветов градации, что и определяет количество кластеров, по которым происходит распределение пикселей. Следовательно, автор использует априорную информацию или формирует гипотезу о числе цветов результирующего изображения. В нашем же случае эта априорная информация применяется в формировании целевой функции для ее последующей оптимизации. Конечно, использование априорной информации об обрабатываемом изображении является недостатком самой СТЗ и понижает ее интеллектуальность. Система, самостоятельно определяющая этот параметр, будет считаться более интеллектуальной, нежели предыдущая.

Целевая функция g(р 1, р2, р3) является функцией 3 неизвестных, где параметр р1 определяет размер маски медианного фильтра, параметр р2 является порогом операции конвертирования с полутонового изображе- ния в бинарное изображение, параметр р3 является количеством морфологических операций над бинарными изображениями. Для оптимизации функции g(р 1, р2, р3) использовалось приложение оптимизации генетическими алгоритмами Matlab Genetic Algorithm Tool со следующими характеристиками: Population Size=80, Creation Function=Uniform, Initial range=[0;1], Scaling function=Proportional, Selection function=Roulette, Elite count=10, Crossover fraction=0.7, Mutation function= Gaussian, Scale=1.0, Shrink=1.0, Crossover function=Scattered, Generations=1000, Stall generations=50, Stall time limit=20, Function tolerance=1e-006. Значения всех параметров остальных разделов идут по умолчанию. На рис. 1 верхняя пара изображений иллюстрирует поверхность целевой функции для маски размерности 1 х 1, а нижняя - маски размерности 10 х 10. Оптимальные значения параметров р2 и р3 изображены темно-синим цветом. Следовательно, существует некоторая совокупность бинарных изображений, на которых достоверно можно определить количество наблюдаемых объектов. Таким образом, задача сводится к нахождению таких параметров, при которых программа «целевая функция» принимает минимальное значение, а измерительная функция СТЗ возвращает бинарное изображение, в котором число пикселей объектов (маски объектов) позволяет вычислить их площадь с заданной точностью (*).

К сожалению, промышленные СТЗ редко решают свои задачи оптимально, что, в частности, зависит от освещенности сцены наблюдения. Статья направлена на оптимиза-

Таблица 1

Программы MATLAB для оптимизации

Измерительная функция СТЗ	Целевая функция
function res=genim(name,p) a=imread(name); b=rgb2gray(a); pp=round(p(1)*10); bb=medfilt2(b,[pp pp]); c=im2bw(bb,p(2)); n=round(p(3)*10); m=[1 0 1;0 0 0;1 0 1]; for i=1:n c=imerode(c,m); end; d=bwlabel(c,8); imshow(~d); xlabel(num2str(p)); res=d;	function res=g(p) buf=genim('money.jpg',p); res=abs(6-max(max(buf(:,:)))); display(strcat(num2str(res),':',num2str(p)));

Havko-

ЖГРАДА

цию (параметрический синтез) управляющих параметров в измерительных функциях СТЗ. Например, в работе [3] описываются отдельные функции СТЗ с возможными значениями управляющих параметров.

Эти параметры были определены экспериментальным путем, но не являются оптимальными. В задаче распознавания микроскопических водорослей [4] измерительные функции СТЗ также определены экспериментальным путем. Достаточно изменить условия освещения, как сразу же падает качество распознавания, что наблюдается также и в ходе решения задачи данной статьи. По убеждению автора, эта проблема разрешается решением задачи (*) в математическом аппарате модифицированных дескриптивных алгебр изображений (МДАИ).

Формализация функции СТЗ в МДАИ

В работах [11–17] можно ознакомиться с математическим аппаратом модифицированных дескриптивных алгебр изображений. Вычислительный аппарат МДАИ демонстрирует достаточную гибкость в описании процессов обработки и анализа в едином математическом пространстве, называемом пространством состояний изображений (ПСИ). ПСИ состоит из МДАИ, представляющих универсальные алгебры на матрицах оцифрованных изображений [8–10]. Аппарат МДАИ является разновидностью дескриптивных алгебр изображений (ДАИ), исследуемых школой академика Ю. И. Журавлева [5–7]. В этом направлении наиболее известны работы его учеников И. Б. Гуревича и В. В. Яшиной [8–10].

Опираясь на работы [11-17], рассмотрим ПСИ, в котором протекают процессы обработки изображений (1).

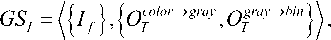
f е {color,gray , bin},             (1)

Элементами ПСИ являются все возможные изображения { I f } , размеры которых одинаковы. Кроме того, в ПСИ все элементы взаимосвязаны, так как оно является пространством состояний. Условно можно выделить следующие правила связей между элементами ПСИ [11; 12]: изменяется хотя бы один пиксель изображения (унарная операция); осуществляется преобразование всего изображения согласно определенному методу (унарная операция); результирующее изображение получается после применения бинарной операции к двум начальным изображениям (поэлементные бинарные алгебраические операции). Все остальные операции могут быть легко сведены к вышеперечисленным

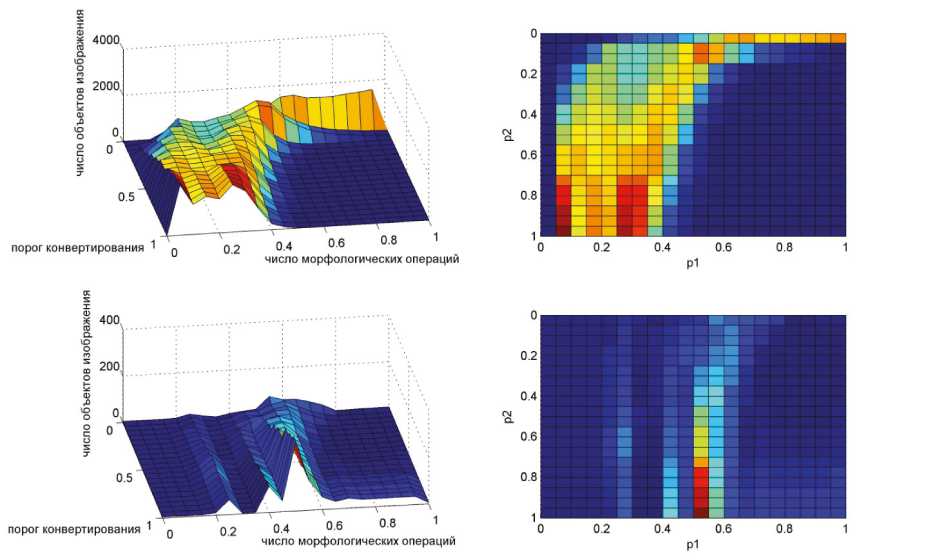
Рис. 1. Целевая функция при маске фильтрации 1 х 1 (верхняя пара изображений) и маске фильтрации 10 х 10 (нижняя пара изображений)

за счет применения свойства ассоциативности, декомпозированы и представлены в виде композиции или суперпозиции базовых преобразований. Подчеркнем, что ПСИ структурно может быть разбито на взаимно не пересекающиеся подпространства (рис. 2) согласно (2).

bin

GS I = ^ G k , k е { color,gray,bin}, k = color

G n G i -® - i * .j

Связь подпространств G k из (2) обеспечивают операции конвертирования { o^ or ^ gray , o gay ^ bin } из (1) [11—16].

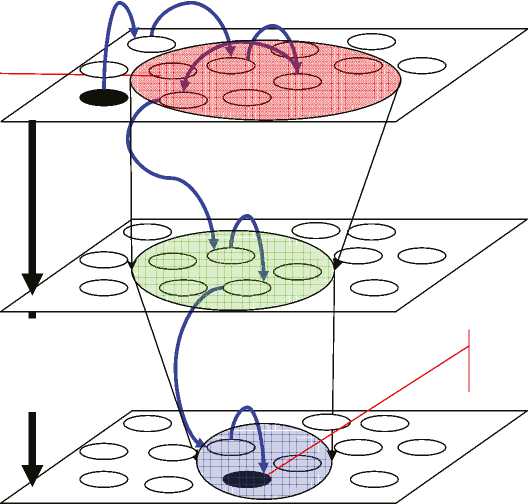
Причем эти операции необратимы и, как следствие, переходы Gbin → Ggray и Ggray → Gcolor невозможны. Согласно работам [11; 12; 15; 16] каждое из подпространств Gk является геометрическим представлением МДАИ Rk, представляющей с алгебраической точки зрения универсальную алгебру конечномерных матриц (реализаций изображений, РИ) с операциями над ними (операции из вышеперечисленного списка). Замкнутость операций над РИ гарантирует, что в результате их применения получится преобразованная РИ той же алгебры. Последовательность преобразований будет описывать маршрут в графе ПСИ. Начальная вершина маршрута будет являться первоначальной РИ, а конечная - РИ, под- лежащей в дальнейшем анализу (измерению выбранного параметры объекта наблюдения). Итак, маршрут в ПСИ описывает процесс обработки изображений (рис. 2). Введем следующее определение.

Определение. Совокупность подмаршрутов, входящих во всевозможные маршруты, которые начинаются с исходной реализации (отмечено на рис. 2 кругом черного цвета в R _color ) и заканчиваются в целевой реализации (отмечено на рис. 2 кругом черного цвета в R _bin ), называется воронкой МДАИ.

Согласно работе [13] математической моделью процесса обработки изображений является Т-ДАСПИ (дескриптивная алгебраическая схема преобразования изображений) (3):

= o Tn ( ( ... O T 1¹ ( i f ; м i ) ... и , ) ,      (3)

где If - начальная вершина маршрута; Ig - конечная вершина маршрута; T„,, е{convert, improve, filter, dis sec t, filter, morph,...}, k=i,m = type(Ti=i,n), H = (hi, --LИn) . Из (3) ясно, что Т-ДАСПИ $RT (ц)(-) является суперпозицией n процедурных преобразований    OTk 1 , . .., O Tknn     с параметра ми Н = (н1, —, Цn) соответственно. Кроме Т-ДАСПИ в аппарате МДАИ используется

GS _I

I f = color

। color^gray T t gray^ bin T

k g = bin

Рис. 2. Структурно-графическое представление ПСИ

^ 1

color

^

gray

^

bin

Havko

ж ГРАДА

еще и Р-ДАСПИ. Согласно [14] Р-ДАСПИ

описывают измерение выбранных параметров объектов наблюдения на РИ (решают задачу анализа изображений) и определяются согласно (4):

О т3 = O Tgray ^ bin (■; Р 2 ) — третье процедурное пре-

образование Т-ДАСПИ.

def m

ok ⁴ = a^-e T ₄      T

_{O T}erode

⁰ bin ^;

к

суперпозиция

,

Г ¹⁰ ' Р3 1

функций

-17

...,

mk

= 1 P ( • ^{, n} j ⁽⁴⁾

где P j = ₁ m e {det erm , probal,struct }, k j = 1, _m =

В МДАИ целевая функция (табл. 1, левая ячейка) будет формально представлена в форме (5) в виде алгоритма:

n money = ^{A lg ( 1} color ’ ^{ p 1 ’ p 2 ’ p 3 ^} ’ na priori )

{

T1    _ cocolor^gray gray OT          (I color; )

i g„ = o r** ( 1 ;„;[ n n ] ) ’ n =П° ■ a1

C = or * bn ( i ;„; P 2 )

C, = O "°‘ ( ••• ( or d ( 1”» ; m ) ’ m ) •••, m ) ’           (5)

суперпозиция k функций

...,

А

четвертое процедурное преобразование

Т-ДАСПИ;

Ц = ( *, ["1⁰ Р 1 "|, p 2 ,

1 0

1 0

, " 10 Р 3 1

m = 0

0 1

0 0

0 1

k =Г ¹⁰ ■ Р з 1

II Ч| = Or ( ¹ b„ ;8 ) ’ rang (I КЦ) = rang ( ¹„„)

n money

n apriori

- max

}

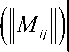
Ее также можно записать и в форме единого выражения (6), используя (3) и (4):

n mon = ^ P

( п ) ( ^ т ( p ) ( I_f ) ) = |

n apr

где n _mon - количество реально найденных объектов наблюдения; n _{ap r} – количество объектов наблюдения априори; п = (8, n apr^ — вектор параметров Р-ДАСПИ; O T = O T^o/or ^ ^gray ( • ;*) - первое процедурное преобразование Т-ДАСПИ; O T = о -.,™ ( • ;[ р ₁₀ p j р ₁₀ p j ]) - второе процедурное преобразование Т-ДАСПИ;

вектор параметров Т-ДАСПИ.

Ранее кратко было охарактеризовано ПСИ на рис. 2. Рассмотрим более подробно его структурно-графическое представление. Итак, ПСИ состоит из трех подпространств в виде МДАИ R _color , R _gray и R _bin . Каждая из них содержит РИ своего вида, связанные правилами перехода между ними. Между МДАИ можно осуществить переходы только за счет операций конвертирования. В каждой из МДАИ имеются окрестности (круги красного, зеленого и синего цветов), РИ которых гарантируют достоверное измерение выбранных признаков после их конвертации. Ясно, что в ходе конвертирования РИ данных окрестностей теряется информация. Последнее означает, что операции конвертирования не реализуют взаимно однозначное отображение МДАИ верхних слоев в нижние. Поэтому размеры окрестностей уменьшаются при таких переходах. Оценка числа РИ, входящих в указанные окрестности, является важной задачей в аппарате МДАИ и позволяет определить количество маршрутов, позволяющих провести качественную обработку первоначальных изображений [11; 12; 15; 16; 17]. Один из возможных маршрутов изображен на рис. 2 последовательностью стрелок синего цвета. Маршрут начинается с цветной РИ в МДАИ R _color и заканчивается в бинарной РИ МДАИ R _bin . Ясно, что переходы из расположенных выше МДАИ к нижним осуществляются только один раз. Следовательно, максимально возможное количество маршрутов будет равно произведениям количеств РИ в каждой из окрестностей, т.е.

N subroad    k color k gray ^kbin ,

где k _color – количество РИ из окрестности в МДАИ R _color ; k gray - количество РИ из окрестности в МДАИ R _gray ; k bin - количество РИ из окрестности в МДАИ R _bin .

Допустим, что в результате обработки изображения получили бинарную РИ Ibin, которая содержит все значимые пиксели (обеспечивающие достоверные измерения) yj, l = 1, kbin наблюдаемого объекта. Следовательно, nm kbin = ЕЕzj, Ibin =1 ЫI, zj ^{0,1}. (8) i=1 j=1

Так как ib,n=I hl1=or-bin (Г; p)=or-bin (| у/1; p)

и zij

' 0, У у <  p ij A y у ^ Р у

, Р у = Р [13],

то величина k _gray будет интерпретировать ся как количество полутоновых РИ I bin , q = 1, k _gray согласно (9), которые преобразуются в единственную бинарную РИ I _bin в ходе их конвертирования.

kbin                                     kbin kXr-y =П(max( j- min( j+1)=П(255 - pl+1)= l=1                                             l=1

kbin

= П ( 256 - p ) = ( 256 - p ) kbin ,            (9)

i = 1

при этом все остальные незначимые пиксели должны в ходе конвертирования преобразоваться в 0. Следовательно, kgray = k1   • kgray, где k1gray - количество полутоновых РИ, конвертируемых в единственную достоверную для измерения бинарную маску, а kg. - количество полутоновых РИ, пиксели которых вне маски будут преобразованы в 0 на бинарной РИ в соответствии с (10).

nm - kbin kgray = П (maX(УУ) -min(Уу) + 1) = l=1

^{nm -} kbin

= П ( ( p - 1) + 1 ) = p nm — kbin .        (10)

l = 1

Используя (9) и (10), вычислим k _gray согласно (11):

k gray = k gray ■ k gray = Р™ " kbin ' ( 256 - p ) kbin =

= p™ • ( 256/ p - 1 ) kbin .          (11)

Г, =|| y j j| = °?'" ^- gray ('* p ) =

= or ^- bin ( |< r ij ,g j ,b j >| ;*),      (12)

где y j = ^{( r} j ⁺ g j ⁺ b j ^)/3 .

Из (12) становится ясно, что для вычисления k _color можно воспользоваться (9), (10), (11) и отсутствием влияния компонентных слоев цветной РИ друг на друга. Тогда k color =^{( k} 'gray • ^k gray ) = ^{( k} gray 7, но ^без анЗЛити^-ческих расчетов это выражение остается всего лишь гипотезой. Итак, из МДАИ R _bin выберем маску и наложим ее на цветную РИ. Тем самым в I c₀l_0r = ||< r ij , g ij , by >|| выделим набор пикселей, соответствующих этой маске, количество которых обозначим k c_olor . Так как

Г =| Ы| = оГ " bin ( I color ; <  *, p > ) = = O g^ray " bin ( or - gray (| < r ij , g j , b j >|| ; p ) ;*),

_|0, |"(rj + gij+ byV3^p ij   I1, ^(ry + gij + bijV3^ p p то

P ^{( r}j ⁺ s i, ⁺ b j )/³ ] ^ p ^ ^ry = s i, = b j ^e [ p ;^255].

Следовательно, kbin kcolor = П (max(ry ) — min(rij ) + 1)(max(gj ) — l=1

• ^{-    min(} g l )⁺¹)(^max( b l ) ^- min⁽ b ij )⁺ 1) = ^kbin                     ₃ ^kbin

= П(255 - p j + 1) =П(256 - p )³ = l = 1                                  l = 1

= ((256 - p ) kbin )³ =( k gray )³.              ⁽¹³⁾

Для всех остальных пикселей, не входящих в маску, выполняется неравенство I(rj + gj + bj)/3 |< p ^ rj = gj = bj е[0;p -1]. Следовательно, nm - kbin k2ray = П ( maX( rl ) - min( rl ) + 1)( maX( gj) -l=1

• ^{-    min(} g ij ) ^{+ 1} )( ^max( b l ) - ^min( b l ) + 1 ) =

n m - kb in                                 з            з

= П ( ( P - 1) + 1 ) ³ = ( P nm - kbin ) = ( k² 2ray ) . (14) l = 1

Havko-

ЖГРАДА

Итак, используя (13) и (14), получим kcolor   kcolor kcolor   (kgray ) (kgray )

Допуская, что между элементами соседних выделенных окрестностей в МДАИ R _color , R _gray и R _bin могут быть попарно установлены всевозможные переходы, можно получить верхнюю оценку уникальных подмаршрутов, содержащихся во всех возможных маршрутах из ПСИ [11; 12; 15; 16]. Для этого подставим (11) и (15) в (7):

nm subroad color gray bin bin p

х ( 256/ p - 1 ) kb” • ( p” • ( 256/ p - 1 ) kb¹’ ) 3 = = k _b„, ■( P "” • ( 256/ P - 1 ) k“" )* =

= p ■k_b i" •( 256/ p - 1 ) * kbi" .        (16)

Оценка (16) показывает, что во всех возможных маршрутах, описывающих процессы обработки изображений в ПСИ, может содержаться указанное число уникальных переходов конвертирования из расположенного выше МДАИ в расположенное ниже. Следовательно, выражение (16) описывает мощность множества маршрутов воронки МДАИ согласно определению.

Итак, мы описали один из столпов дескриптивного подхода к обработке, анализу и распознаванию изображений с применением модифицированных дескриптивных алгебр изображений. В работах [11–17] предлагалось исследовать и описывать в виде дескриптивных математических моделей процессы обработки реализаций изображений. В настоящей статье приведены количественные показатели, необходимые для оценки этих математических моделей. Выражение (5) демонстрирует одну из таких моделей, нужную для количественной оценки площади наблюдаемых объектов. На рис. 2 изображено пространство из трех подпространств, которое содержит формализованное описание любого процесса обработки изображений. Для заданных начальных и конечных реализаций изображений вводится понятие воронки МДАИ. Размер воронки МДАИ определяется выражениями (7) и (16). Воронка МДАИ состоит из трех сечений, размер каждого из которых можно оце- нить формулами (8), (11) и (15). Выявленные количественные оценки необходимы в дальнейших теоретических и прикладных исследованиях в области автоматического проектирования и разработки систем технического зрения.