Параметрическое оценивание авторегрессии при автокоррелированных помехах в выходных сигналах

Самарская государственная академия путей сообщения

В статье рассматривается устойчивый численный метод решения задачи минимизации отношения двух квадратичных форм, что позволяет находить оценки параметров авторегрессии при конечной выборке, при наличии автокоррелированных помех наблюдений.

Пусть имеет место случайный процесс авторегрессии конечного порядка, описываемый следующим стохастическим линейным разностным уравнением порядка r с дискретным временем i = ..., - 1, 0, 1,...: r

и

T = { t ; t <  i , t e Z_c - множество целых чисел } .

• 3)    Случайные процессы    { l i ( i

l ₂ ( i ) } статистически независимы.

N ^{- 1} E l 2 ( i ) l 2 ( i + m ) ^^ h l ( m ) < ”

N ^ю ^2          , i=i о

Z i - E b . * ) Z i - m = 6(0,        (1)

m = 1

y. = Z . + l a ( i )

где Z_i , y_i – наблюдаемый и ненаблюдаемый векторы состояний системы, ξ ₁ ( i )- генератор авторегрессии, ξ ₂ ( i ) – коррелированная помеха. Требуется определить оценку b ^ˆ( N ) по y_i .

m = 0,..., r где h*2 (m) - локальная автоковариационная функция, H* - положительно определенная матрица

Пусть выполняются следующие условия:

	h * 2 (0)	h * 2 (1)      .	.     hl( r )
H * 2 =	2 (1) ...	h * 2 (0)    . ...             .	.   hl( r - 1) .             ...
	h * 2 ( r )	hy r - 1) .	.      h * 2 (0)

~

T

*

= h J (0) ■ ( hy

• 1)    Случайный процесс ξ ₁( i ) удовлетворяет условиям:

El 1 ( i + 1)/ F ) = 0 п.н.;

El 1² ( i + 1)/ F ) = C ( i + 1) <  п <ю п.н.;

E ( l 4 ( i )) <  п <ю .

~ *

ξ ₂

H l

,

• 2)    Случайный процесс ξ ₂ ( i ) удовлетворяет условиям:

  где

  
  

Ei ₂( i + 1)/ F ) = 0 п.н.;

h ;₂(0)    ...   h * 2 (r - 1)

...            ...            ...

h ;2 ( r - 1)  ...     F2 (0)

^E (Ft i о )) <  ^п <^ю ;

H * ξ ₂

,

E Ц( i +1)/f) < w , где W - случайная величина, E(W) < п < ^ , E-оператор математического ожидания, Fi- у – алгебра, индуцированная семейством случайных величин lk(t),t e Ti} , k = 1,2, hl2 = (h*2(1),-,h*2(r))T e Rr.

5) Множество, которому априорно принадлежат истинные значения параметров

( b 0⁽¹⁾ ,...,

~~ bnr))1 g B компактно, B g R .

0 r

• 6)    Для случайного процесса Z_i существует предел:

N lim N-XZr (i)ZT, (i) = HZz

N >^

i =1

где

Z ( i ) = ( Z ,,..., Z ) ^T g R . r                    i - 1 , , i - r                r

Представим уравнение (1) в виде:

Ув = yT (i)b о + § 1(i)+ § 2(i)- 5 Tb 0, где

У г ⁽ i ) = ⁽ У -1 ,-, У - r ) ^{T g R} r ,

5 r = ( 5 2 ( i ),..., 5 2 ( i - r )) ^T .

Введем обобщенную ошибку:

e ^{( b} 0 , i ) = y i ^- y ^{T (} i ) ^b О = § 1 ⁽ i ) ⁺ § 2 ⁽ i ) ^{- 5 T b} 0 .

Средняя дисперсия обобщенной ошибки равна:

2N a e = lim N-1 XE(e2(b0,i)) = h^ (0) + N >^                        ’l i =1

+ h | ₂ (0) + ( Я * ₂ b 0 , b 0 ) - 2( h * 2 , b 0 ) = ro(b 0 ), где (.,.) - скалярное произведение.

Определим оценку (б ( N ) ) неизвестного истинного значения параметра ( b ₀ ) из условия минимума суммы взвешенных квадратов обобщенных ошибок e ² ( b , i ) с весом ω ( b ), т.е. [1]:

N min го-1 (b)X (yz- - yT (i)b)2 = (b )g B Rr min го 1( b )UN (b)

( b >B c R_r                 ’

где

N

U n ( b ) = X ( У - У Т (i) b ) 2 .

i = 1

Утверждение 1. Пусть некоторый случай- ный процесс {yt, i =

..

.,-1,0,1,...} описывается уравнением (1) с начальными нулевыми условиями и выполняются предположения 1-5.

Тогда оценка bˆ(N) определяемая выражением (2) с вероятностью 1 при N®® ҐҐ, существует, единственная и является сильносостоятельной оценкой, т.е.

b( N ) -^ b 0 ,

N ^^

при этом

N

- 1

¹ min ro ¹ ( b)U_N ( b ) =        ^{N (}^⁰) = 1

( ^b ) g ^b c R r            ^NV^        ro ( b ₀ )

.

Доказательство . Рассмотрим функцию:

N

N ^{- 1} U n ( b ) = N -¹ X ( Z i + ^ 2 ( i ) - ( Z r ( i ) + 5 r ) ^Tb ) = i = 1

N

= N ^{- 1} X ( ^ 1 ( i ) + ^ 2 ( i ) + Z T ( i ) b 0 - ( Z r ( i ) + 5 r ) ^T b ) = i = 1

N ²

= N ^{- 1} X ( 5 1 ( i ) + ^ 2 ( i ) - Z T ( i )~ -5 r ^Tb ) = i = 1

= S1+ 32 + 33, где ~ b = b - b 0;

N

• 3 ,    = N -‘X ( 5 1² ( i ) + 5 22 ( i ) + b^T 5 r ( 5 r ) ^Tb - i = 1

• - 2( 5 1 ( i ) + 5 2 ( i )) 5 r ^Tb );

• 3 2 = N ^- X ~ ^T Zr ( i ) Z r^T ( i ) ^b;

i =1

• 3 = 2 N - ¹ X (( - 5 2 ( i ) - 5 1 ( i )) Z T ( i ) ~ + i = 1

• + Z^T , ( i )~ 5 T b + 5 , ( i ) 5 2 ( i )).

Из предположений 1-5 получаем:

• ³ ‘ ^-—^ ^h ^‘ (0) + h i (0) + ^bTH 2 ^b - ²( ~i ) ^Tb ;

• V b g R_r .

• 3 2 ^П -. > b ^T H*_ZZb; V b g R r . N ^^

• 3 П . - . _>  0, V b g R .

• ³ N >^

Окончательно имеем

N ^{- 1}U n ( b ) ——> h (0) + h | (0) + b^TH*b - N >ю              2¹           2¹

• - 2( h /2 ) ^Tb + b ^tH Zz ~ =

= b^T ( H Zz + H ₂ ) b - 2( H Zz b 0 + ~ ₂ ) ^Tb +

+ h * (0) + h^ (0) + b T H zz b 0 = U ( b ), V b e R r .

Покажем что решение задачи min to ^— 1 ( b)U ( b )

существует и достигается в единственной точке b ₀ , т.е.

~       U ^~ ( b 0 )

min to ¹ ( b)U ( b ) =-------= 1

( b ) e B R r              ^V ’    to ( b ₀)        . ⁽³⁾

Для этого рассмотрим функцию

V ( b,O ) = U(b ) — Oto ( b),O e R 1 ,

V(O ) = ₍ min V ( b,O ).

( b ) e B c R r

Дифференцируя V ( b , θ ) по b и приравнивая производную к нулю, находим b ( θ ) , и тогда

V (O ) = h * (0) + h * (0) + b T H zz b 0 — Oh * (0) —

—

Oh * (0) — ( H Zz b 0 + h * 2 — Oh'^^T X

/ T T *    . T T * ATT* \ — 1     / T T *  7    .  7 * Л7 * \

^{X ( H} ZZ ⁺ H E , 2 ^{— OH} E, 2 ) ^{X ( H} ZZ ^b 0 ^{+ h} E 2 ^{— Oh} E 2 ) .

Легко проверить, что уравнение

V(O) = 0 на интервале (—да, Amin +1) имеет не более одного корня. Где λmin – минимальное собственное значение матрицы HZZ. Непос редственной постановкой O1 = 1 в уравнение

V(O) = 0 легко убедимся, что этим един ственным корнем на интервале (—да, 2min +1) является O1 = 1. Тогда непосредственно следует справедливость (3). Получаем, что с вероятностью 1 при N > ГГ решение задачи (2) существует и является единственным т.е. с вероятностью 1 при N > ГГ существует единственная оценка bˆ(N) и b(N)   п.Н. > b0

0 ,

N >да

N ^— ^min to ^— 1 ( b ) U n ( b ) пп ■ >  1

( b ) e B c R r                     N >да     ^-

Из утверждения следует, что для получения сильносостоятельных оценок (2) требуется априорное знание лишь отношение γ средних дисперсий генерирующих шума

{ E 1 ( i ) } и аддитивного шума измерений { E 2 ( i ) } ■

Далее показан численный метод построения оценок параметров авторегресии с ав-токорреллированными помехами в выходных сигналах на основе введенного нелинейного метода наименьших квадратов, представляющего собой отношение двух квадратичных функций [2].

Для получения конструктивного метода вычисления оценок из критерия (2) рассмотрим вспомогательную функцию:

V n ( b , O ) = U n ( b ) — Oto ( b ).

Лемма       1.       Уравнение vn (O) = , jmin Vn (b,O) = 0 имеет не более ( b )G B c Rr одного корня θˆ(N) на интервале (—да, AminiN )).

где λ _min( N )- наименьший корень уравнения:

det[ A Y A_y — OH * ] = 0.

Если    θ ^ˆ( N )    существует, то

0 <  O(N ) <  A _min ( N ), т.е. O ( N ) - наименьший среди всех корней уравнения V(O ) = 0 , где

A Y =

y N — 1

У 1 — r

...

y N — r

Выражение

V n ( b ,O ) = Y^TY — O ( h ^(0) + h ^(0) ) +

+ b^T ( A Y A_y — OH * ^ b — 2 Y^t A_y — Oh T ) b .

Дифференцируя V_N ( b , θ ) по b и приравнивая производную к нулю, находим

b ( N,O ) = ( a Y A y — OH * )^{— 1} ( a Y y — Oh * )

и тогда

V n (O ) = Y^TY — O ( h *(0) + h *(0) ) +

+ Z ^ ^T ( N ,O ) ( A Y A_Y — OH * )^ ( N ,O ) —

• — 2 ( A Y y — Oh E * f b ( N , O )

или

V n (6 ) = Y T Y - 0^ (0) + h j (0) ) -

• -(ATY - 6^ ) (a a - 0Hj)"' (A. Y - *£ ).

Заметим, что V_N ( θ ) на интервале

( - да , A min ( N ) ) непрерывная и

V n (6 ) = - ( h j (0) + h j (0) + b^T ( N , 6 ) x

T

H j, b(N , 6 ) - 2 ( h j ) b(N , 6 ) J .

Отсюда ясно, что    V N ( 6 ) <  0,

• V 6 е ( - да , A min ( N ) ) и доказательство леммы.

Лемма 2 . Для функции V_N ( θ ) справедливо следующее утверждение:

• ') все корни уравнения V_n (6 ) = 0 неотрицательны (если они существуют).

• 2) уравнение V_n (6 ) = 0 на полусегмен-

• ность {6(i)} определяется следующим алгоритмом:

Шаг '. 6 ‘ ( 0 ) = 0.

Шаг2. S ^A a^ ( N ) + 0' ( i - 1 ) ) /2.

Шаг 3. Вычисляются b ( N,6'(г ) ) из уравнения:

( A T A y - 6'(i ) H j b(6'(i )) = ( A T A y - 9'(i )~ j ) .

Шаг 4. Вычисляется

V n (9'( i )) = Y^TY - 9'( i ) ( h j (0) + h j (0) ) -

• - ( A T Y - 6 '( i ) ~ j ) T b ( N , 6 '( i )).

Шаг 5. Проверяется условие

V n ( 6 '( i )) <  0.

Тогда, если уравнение Vn (6) = 0 имеет корень 6(N) е [0, Amin(N)), то последова- те [0,λmin(N)) имеет не более одного корня.

3) существование корня θ ^ˆ( N ) на полусегменте [0, λ _min ( N )) является необходимым и достаточным условием существования единственного решения (2), при этом

тельность

ˆ

ˆ

ˆ

ˆ

6 '(0),..., 6 (0)    конечна и

min го "' ( b)U_N ( b ) = ^N^-----

^{( b )}e 8 ^ R r                      to( b ( N )) ,

где b (N) = ( aYay -

6 (0) е [ 6 ( N ), A min ( N )), в противном случае последовательность бесконечна.

Доказательство утверждения непосредственно следует из леммы 2.

Утверждение 3 . Пусть существует

6 (0) е [S( N ), A „_n( N )), тогда li^J ⁶ ( i ) = ⁶ ( ^N ),

ˆˆ  ˆ

^да ^b ( ^N , ⁶ ( i )) = ^b ( ^N ), где 6(i ), b(N,6(i )) оп-

р

6 ( N ) H j ) ^- ' ( A T Y - 6 ( N )~ 2 )

Эта лемма по сути дела доказана при доказательстве леммы 1.

На основании доказанных лемм получены численные методы, которые позволяют:

• -    ответить на вопрос существует или нет единственная оценка b ( N ) ;

• -    определить начальное приближение, гарантирующее сходимость итерационного процесса к единственной оценке b ( N ) ;

• -    вычислить с любой наперед заданной точностью оценку b ( N ) .

Утверждение 2 . Пусть последователь-

еделяются следующим алгоритмом:

Шаг '. Вычисляется b ( N,6(i ) ) из урав-

нения (4).

Шаг 2. Вычисляется

6(i +') = (hj (0) + hJ (0) + bT (N, 6(i)) x x HJ b( N, 6( i)) - 2( hj ) T b( N, 6( i)))-' (YT Y +

+ 6(i ) b^T ( N , 6(i )) H j b ( N , 6(i )) - 6(i )2( h j ) ^T x x b ( N , 6( i )) - ( A1 T Y - 6 ( i ) h * 2 ) T b ( N , 6( i )) ) .

Шаг 3. Переход к шагу 1.

Доказательство . Утверждение 3 вытекает непосредственно из метода Ньютона

ˆ

ˆ

9( i + 1) = 0( i ) -

А /

V N ( θ ^ˆ( i ))

/ V N (в( i )).

Обоснованность использования метода Ньютона следует из того, что V_N ( θ ) – непрерывна We[0,^ N )), V_N (0 ) <  0, V 0 e ( -« , WN ) ) и

V n ( 0 ) = - 2 b T ( 0 ) H * ( A Y A_y - 0 H * 2 ) ^{- 1} H * 2 b( 0 ) -- 2(~ ; ₂) T ( h ^) ^{- 1} ~ 2 + 3(~ 2 ) T ( a Y A y - o h * ₂) ^{- 1} x x H*^b(0 ) + b T (0 ) H ( a Y A y - o h * ₂) ^{- 1} ~ 2 < о, V 0 e [0, 2 min ( N )).

На практике вычисления прекращаются, если достигнута заранее заданная точность, т.е. если выполняется условие:

y_t = Z i + ^ 2 ( i )

где ξ ₂ ( i ) - аддитивная локальная автокорре-лированная помеха выходного сигнала с дисперсией σ_ξ ² , которая изменяется в зависи-

σ ²

2       ξ 2

мости от y ( ^G Z =---, a 2 - дисперсия сиг-

γZ

I V_N (0( i + 1)) - V n Q i ))[

II V n (0(i + 1))||

< 5

,

где δ – априори задаваемая точность нахождения оценок.

На базе описанного математического

нала Z_i ). Для цели исследования состоятельности оценок использован большой объем выборки N= 500. Параметр γ дискретно принимает значения 0,5, 1, 2, 3, 4.

Результаты оценок параметров, полученные классическим и модифицированным МНК посредством программных алгоритмов математического пакета, приведены в табл., где

5 = V( b i - b i ) 2 + ( b 2 - b 2 ) 2 x 100%,

5^МЯ ^ =V ( b r ^K - b 1 ) 2 + ( b T ^K - b 2 ) 2 x 100%, b^ , b₂ - вектора оценок модифициро-

алгоритма реализован пакет прикладных программ в среде MathCAD для параметрической идентификации линейных разностных уравнений при наличии локально автокорре-лированных помех в выходных сигналах.

В основе программного алгоритма задана тестовая модель авторегрессии (1) со следующими исходными данными:

r= 2 – порядок авторегрессии; Z_i – вектор выходных значений, где i =1,2,3… индекс нумерации дискретных моментов времени;

ванного МНК;

1> 1 М ^НК , Z ? 2 ^MНК - вектора оценок классического МНК;

δ , δ^МНК – погрешности оценок пара-

метров.

Из анализа (рис. 2, рис. 3, рис. 4) откло-

b =

f 1 1

(- 0.25 J

– вектор “истинных” парамет-

ров; ξ ₁( i ) - генератор авторегрессии как последовательность независимых случайных величин; ξ ₂ ( i ) – автокоррелированная помеха как последовательность зависимых величин. Соответственно уравнение авторегрессии будет представлено выражением:

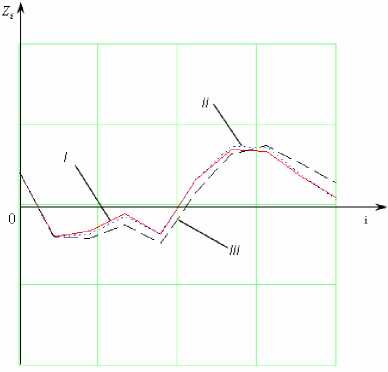
Рис.1. Выходной сигнал Z_i, рассчитанный с

b )          .

I ; II - нелинейного a J

r

Zi -E b0 m) Z- m = ^ 1( i ), m=1

параметрами: I – “истинными”

а наблюдаемый сигнал:

МНК

f b ; 1                       f b^ М ^нк 1

J ; III - стандартного МНК а мнк

V a J                      V a J

Таблица. Сравнение точности векторов оценок параметров авторегрессии по классическому е । T aeo eoedT аан T i о I ^ E аёу N=5001 de ёnce^ ^ uo b 1 = 1, b₂= -0,25

σ 2 γ = ξ 2    2 σ Z	МНК			М одиф ицированны й М НК
	b ˆ 1 М Н К	b ˆ 2 М Н К	δМНК %	b ˆ 1	b ˆ 2	δ %
0,5	1 ,078	-0,268	13,1	1 ,003	-0,258	3
1	1 ,1 1 1	-0,26	11	0,98 1	-0,23	4,4
2	1 ,176	-0,303	23,5	0,965	-0,23	5,2
3	1 ,249	-0,36	26	0,98 8	-0,259	7,6
4	1,29	-0,392	34,2	1 ,006	-0,276	7,2

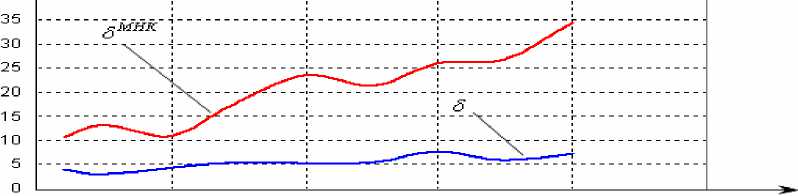
S°A *

0               1                2               3               4               5        у

Рис. 2. Сравнение δ(γ), δМНК (γ) отклонений векторов оценок параметров авторегрессии классическим и модифицированным МНК.

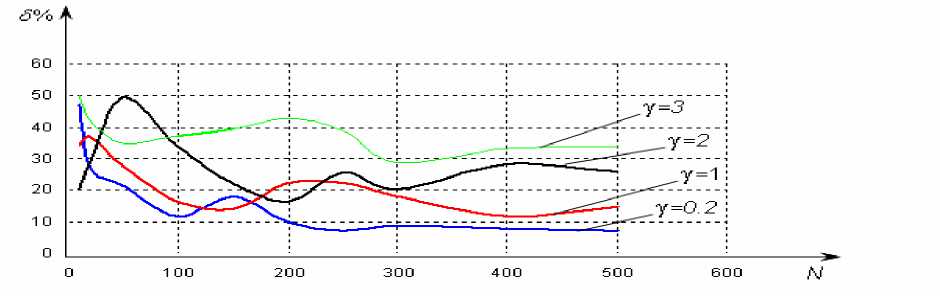
Рис. 3. Сравнение δМНК (γ) отклонений векторов оценок параметров авторегрессии классическим МНК от векторов “истинных”’ параметров при gg = {0.2, 1, 2, 3}.

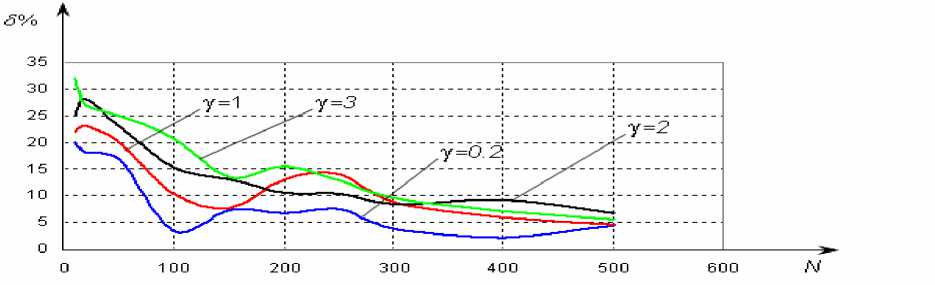
Рис. 4. Сравнение δ ( γ ) отклонений векторов оценок параметров авторегрессии модифицированным МНК от векторов “истинных”’ параметров при gg = {0.2, 1, 2, 3}.

нения оценок от истинных параметров и выхода рассчитанного сигнала от истинного (рис. 1) вытекает, что при большом объеме выборки модифицированный МНК дает удовлетворительные результаты при любых значениях γ . Оценки стандартного МНК ухудшаются с увеличнием γ , соответственно с увеличением дисперсии помех наблюдений ξ ₂ ( i ) погрешности δ^МНК становятся достаточно значимыми.

Следовательно, на приведенном примере показывается менее точный результат классических оценок МНК при наличии аддитивных ошибок измерений в процессе авторегрессии и состоятельность предлагаемых.

В статье описаны конструктивные методы построения оценок параметров авторегрессии; показаны условия существования и единственности этих оценок. Предложенные вычислительные алгоритмы позволяют находить нелинейные МНК – оценки параметров авторегрессии, используя лишь стандартную процедуру решения линейных алгебраических уравнений, эти алгоритмы приспособлены к обработке больших массивов исходной информации для динамических систем высокого порядка.

Реализован пакет прикладных программ в среде MathCAD для параметрической идентификации авторегрессии при наличии ло- кально автокоррелированных помехах в выходных сигналах. Получена авторегрессионная модель прогноза состояния пути, которая нашла применение при планировании и производстве путевых работ на железнодорожном транспорте [3].