Параметрическое преобразование в ферромагнетике сдвиговой поверхностной волны движением удерживающей доменной границы

1 Ульяновское отделение Института радиотехники и электроники РАН 2 Институт радиотехники и электроники РАН, г. Москва

Рассмотрено параметрическое преобразование в кубическом ферромагнетике сдвиговой поверхностной волны равномерным движением 180-градусной доменной границы.

Доменные границы (ДГ) сегнетоэлектриков и ферромагнетиков способны, как известно [1,2], удерживать соответственно элек-трозвуковые и магнитоупругие сдвиговые поверхностные волны (СПВ). Параметрическое преобразование в сегнетоэлектрике элек-трозвуковых СПВ движением ДГ обсуждалось недавно в работах [3 - 5]. В настоящей работе предпринимается аналогичная попытка в отношении магнитоупругих СПВ в ферромагнетике.

Обобщение результатов работы [2] на случай равномерного движения 180-градусной ДГ типа блоховской стенки основано ниже на использовании простейшей модели геометрической ДГ. Уточним ограничения, вносимые ею в связи с действием дополнительного фактора - движения ДГ.

Принято считать, что инициированное внешним управляющим воздействием движение ДГ не сопровождается структурными изменениями последней, если скорость ДГ V d <  ^vw , где v_w - предельная Уокеровская скорость [6]. Следует, однако, заметить, что структурная устойчивость ДГ при стационарных режимах движения определяется, во-первых, равновесными термодинамическими условиями, в которых находится кристалл, а во-вторых, - его технологическими качествами (наличие дефектов, примесей и пр.). Поэтому она по-разному проявляет себя в массивных и пленочных образцах.

Вышеуказанное ограничение на скорость ДГ характерно, как раз, для массивных образцов вдали от фазового перехода. Учитывая обычное для кубических ферромагнетиков неравенство vw > ct, где ct - скорость сдвиговых волн без учета магнитострикции, дополнительное к требованию геометричности ДГ в масштабе длин волн kA << 1 ограничение на ее скорость примем в виде V D < ct. Кроме этого, подразумевая использование безобменного магнитостатического приближения, условимся, что k < kmях , k2XD << Hn, где D - обмен-maxmax        a ная константа ферромагнетика, Ha - поле анизотропии, k - волновое число СПВ, не превосходящее порогового значения kmax , A - фактическая толщина ДГ.

Положим, что (010)-ориентированная 180-градусная ДГ движется вдоль оси у лабораторной системы отсчета x 0 yz и имеет текущую координату y_D = J^t , t - время. Распространение сдвиговых волн в плоскости х 0 у со смещениями u j в доменах ^{( j} = 1 ^пр^и у >  y D , ^j = ^{2 п}р^и у <  y D ) ^подчиним условиям:

И, || z || M (^j ) , АГ"' ?^ М Г(²\ /1111 s s            s

Замечая, что внутренние магнитные поля доменов H (^j ) || z - есть поля анизотропии, напишем

M si ) = ( - 1) ^j M s , Z/ ' ^j) = ( - 1) ^{j + 1} H a , (1)

где Ms - спонтанная намагниченность. С учетом (1) и оговоренных условий распространения из уравнений Максвелла, линеари- зованного уравнения движения магнитного момента и уравнения движения теории упругости получим в безобменном магнитостатическом приближении следующие уравнения

д 2 и д t2

=c V u + ' '‘"' ^ V 2 ф„ t j    4 п M s р    ^J

д      9

--у + to ² Гф. =

д t2     k

- 4 п/в® о ( ^_ ') j ^{+ 1} V ²Uj .

цируемых на ДГ распространяющейся СПВ, to ² = to k - to ² + s ² V 2, k и p имеют смысл продольной и поперечной ДГ компонент полного волнового вектора СПВ K = k + p , s - коэффициент амплитудного спадания, Q и to - частоты колебаний СПВ в сопутствующей ДГ и лабораторной системах отсчета, связанные соотношением

V

rr

to = □ + KVD =□ + pVD .   (4)

Здесь V - оператор Гамильтона в плоскости x 0 y , ф j - магнитостатический потенциал, to о = Y H a - частота однородной прецессии, to k = [ to о ( to o + to м )]^1/2 - частота магнитоакустического резонанса, to м = 4 пу M s - частота намагничения, Y -гиромагнитное отношение, Р - магнитоупругий коэффициент, р - плотность.

Для построения решения уравнений (2), описывающего СПВ на движущейся ДГ, воспользуемся аналогично [3 - 5] приемом перехода в сопутствующую ДГ систему отсчета с применением преобразования Галилея. Поскольку в безобменном магнитостатическом приближении имеет смысл рассматривать только низкочастотную ветвь спектра магнитоупругих сдвиговых волн при

Вытекающие из (2), (3) связи величин K , p , s между собой выглядят следующим образом

p =

V_D to 2 to ² - to k + c 2 ( K ² - s ² ) c t c t         to ² - Xto0

_K 2 =2 to ² ( s ² + to ²/ C t ² ) - Xto o ² s ²

K = to ----,777--- to 4 + 4s 2 to 2V2

7                  7

₊ 4s 2 _to 2 VD ^{to -} X^to0 ^{+ s} c t c² to ⁴ + 4s ² to ² V ²

В формулах (5), (6) обозначено:

— 2     2     2 , 2ТЛ2

to = to k - to + s VD,

, (5)

to > to l , to l = ( to 2 - Xto 2 )¹ / ²,

x = yP ² / ^ M s to ₀ - безразмерная константа магнитоупругой связи, Л - модуль сдвига, то ввиду требования ограниченности решения уравнений (2) приходим к единственной возможности представления СПВ на движущейся ДГ:

ф j

^{4 п};^р щ|'| j ^{+ 1}

= Ф j---------------------- u j , j to ² + i2 to sV D ( - 1) j j

_u. = и , e (kx + py -^{Ю 1} ) _e ^{( - 1) J} s ⁽ y ^- y D )

, (3)

_ф j = F j _e i ( kx -n t ) _e ( - 1) j |k|( y - y_D )

.

В выражениях (3) Ф j - потенциалы полей рассеяния магнитных полюсов, инду-

s ² = s ² (1 - V²_d / c² y = 2  —2    2

to ² = to ² - xto 02 .

Полное спектральное представление СПВ завершает дисперсионное соотношение s + xto0^----G^to’VD ‘----1 k |= 0. (7)

1 + Xto 0 F ( to ,V D )

Оно следует из равенства нулю детерминанта системы однородных алгебраических уравнений, образующихся при подстановке выражений (3) в стандартные граничные условия непрерывности на ДГ сдвиговых смещений, напряжений, потенциалов и нормальных компонент магнитной индукции. В уравнении (7) о = k /| k | - знаковая константа, вводимая с целью явного описания невзаимных эффектов при распространении СПВ, а функция F ( to , V d ) задается равенством

F ( to , V_D ) =

to ² + 2 pV_D to

4 . л 2тг2   2

to + 4 s V d to

Что касается функции G ( to , V d ) , описывающей реакцию магнитной подсистемы посредством полей рассеяния, то она имеет громоздкий вид и поэтому в явном виде не приводится. Достаточно заметить, что ее полюса определяют частоты ферромагнитного резонанса (ФМР) на полях рассеяния

Oto M ±V to M - 4 s²vD ω = σω +

⁰               2

, (9)

а нули указывают на наличие антирезонансного отклика магнитной подсистемы.

В частном случае статичной ДГ V d = 0 имеем согласно (8) F ( to ,0) = - 1/ to ², где to ² = to k - to ² . Функция G ( to , V d ) при этом существенно упрощается и принимает вид

toto 1

^{G ( to ,0)} = ^{-( to} --) ~ .

to - Oto ₀ to ²

Как следовало ожидать, дисперсионное уравнение (7) переходит в итоге в дисперсионное соотношение работы [2]

σχω ω ω s+Ik| , % (to--°-M-) = 0. (10)

to2 - to £      to - Oto 0

Характерной особенностью СПВ при Vd = 0 является наличие верхней точки обрезания спектра обратных ( k < 0 ) волн в условиях антирезонансного отклика магнитной подсистемы на частоте to* = to 0 G/1 + 4to M I to 0 -1)/2 . (11)

Ветвь прямых ( k > 0 ) СПВ также ограничена сверху. Однако это ограничение носит асимптотический (в коротковолновом пределе k ^ ^ ) характер и, ввиду близости ограничительной частоты спектра to0 (1 - %) низкочастотной линии спектрального дуплета (9), имеет явно резонансную природу. Бла-„ * годаря тому, что to £ заметно превышает to из (11), спектр обратных СПВ не выходит за пределы линейного (квазиакустического ) участка. Отсюда вытекает, что возможные преобразования обратных волн движением ДГ будут заведомо слабыми (нерезонансными). В дальнейшем, поэтому, ограничимся рассмотрением только прямых волн.

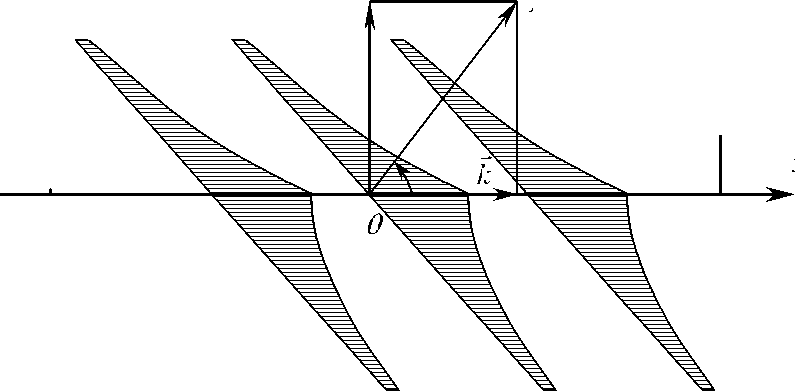
Выражения (3) - (6) показывают, что аналогично электрозвуковым волнам [3 - 5] волновая нормаль магнитоупругой СПВ подвержена ориентирующему действию со стороны движущейся ДГ. Типичная картина волновых фронтов и распределения вдоль них сдвиговых смещений (3) СПВ на движущей-

——

P

—

K

y

— и

V D

k

q

Рис. 1. Схематическая картина распределения сдвиговых смещений в неколинеарной ( 0 < 6 < П /2 ) СПВ на движущейся блоховской стенке. Угол 6 между волновым вектором K СПВ и его проекцией k на ДГ характеризует поворот волновой нормали под влиянием движения ДГ - "флюгерный" эффект

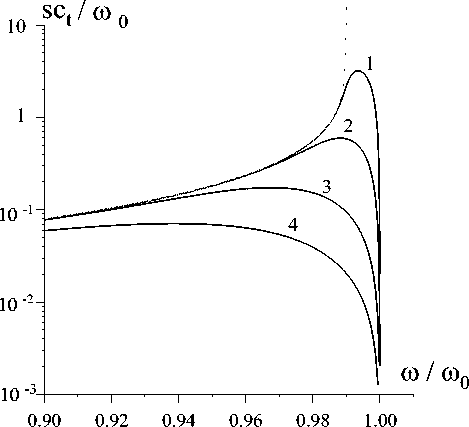
Рис. 2. Частотные зависимости коэффициента локализации СПВ для случая X =0,01 и tom / to0 =0,5: 1 - VD /Ct =0,001; 2 - VD /Ct =0,01;

3 - V_D / C_t =0,1; 4 - V_D / C_t =0,5

ся ДГ представлена на рис.1. Угловое отклонение волновой нормали при такого рода "флюгерном эффекте" составляет величину 9 = arctan( p / k ) . Неколлинеарность полного

r волнового вектора K направлению вдоль границы в сочетании с сохранением граничной локализации и стационарности распространения (Im(k) = 0, to > 0 ) позволяет классифицировать СПВ как специфическую разновидность граничных волн - неколлинеарную граничную волну.

Пряиым следствием неколлинеарности СПВ является вытекающее из (4) неравенство частот колебаний сдвиговых смещений и потенциалов полей рассеяния: to >Q , pV_D >  0 . Существует, поэтому, принципиальная возможность регистрации неколлинеарной СПВ по биению результирующих магнитостатических колебаний (описываются потенциалом ф j ) в момент пересечения приемником линии движущейся ДГ.

Спектральные характеристики СПВ получаются численным решением уравнений (5) - (7). При выборе to в качестве независимой переменной и учете в (7) представления | k | формулой |k |= (K2 - p2)1/2, в результате последовательного исключения p и K согласно (5), (6) приходим к одномерному нелинейному уравнению для определения s . Последующей подстановкой to и s в (5), (6) можно легко найти все остальные параметры СПВ.

Расчеты показывают, что основные изменения спектра СПВ под влиянием движения ДГ происходят в полосе частот to ₀(1 — X ) - to - to ₀ с относительной шириной, равной X . Как видно из рис. 2, 3, здесь СПВ имеет тем большую степень граничной локализации и тем более глубокий минимум частотной зависимости фазовой скорости продольного распространения v = to / k , чем меньше V d / c_t . Вследствие неограниченности возрастания s при V d / c_t ^ 0 (см. штриховую кривую на рис. 2) СПВ прямого распространения не существует на статичной ДГ при частотах to > to ₀ (1 - X ) • Пороговое значение частоты to = to 0 (1 — X ) выступает при этом коротковолновой ( k ^^ , v ^ 0, см. штриховую кривую рис.3) асимптотической границей спектра СПВ [2].

Движение ДГ снимает данное ограничение на спектр СПВ и ввиду существенного (при V_D / c_t - 10 ^{— 3} , см. кривую 1 рис.3) за-

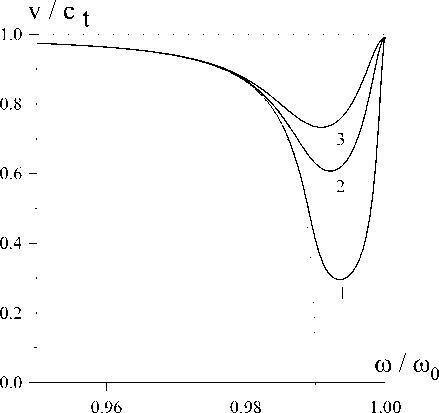
Рис. 3. Частотные зависимости углового фазовой скорости СПВ при X =0,01 и to m / to 0 =0,5:

1 - V_D / C_t =0,001; 2 - V_D / C_t =0,003; 3 -

V_D / C_t =0,005

медления продольного распространения СПВ вынуждает здесь считаться с возможностью нарушения условия геометричности ДГ из-за роста | k | . Впрочем незначительное увеличение скорости ДГ (кривые 2, 3 рис.3) позволяет легко избежать указанной неадекватности модели.

Кривые 1 - 3 рис.3 лежат выше штриховой кривой, что свидетельствует об увеличении фазовой скорости СПВ в результате движения ДГ. Аналогичным образом из рис.2 заключаем о делокализации колебаний СПВ под влиянием движения ДГ. Установленные закономерности преобразования спектра СПВ объясняются увеличением ее средней энергии в результате работы, совершаемой внешним источником над системой "волна -граница" в процессе вынужденного перемещения ДГ. Образование минимума частотной зависимости фазовой скорости СПВ в интервале [ щ ₀(1 - х ), © ₀] можно при этом рассматривать как следствие типичного вырождения выходящей на асимптотический предел своего спектра ветви СПВ для статичной ДГ с линией ФМР полей рассеяния. Заметим, что аналогичное вырождение линий ФМР полей рассеяния (соответствуют частотам (9) при V_D = 0 ) под влиянием движения ДГ отмечалось для магнитостатических поверхностных волн [7]. Формула (9) описывает указанный вырожденный спектр магнитостатических поверхностных волн на движущейся ДГ при отсутствии магнитной диссипации.

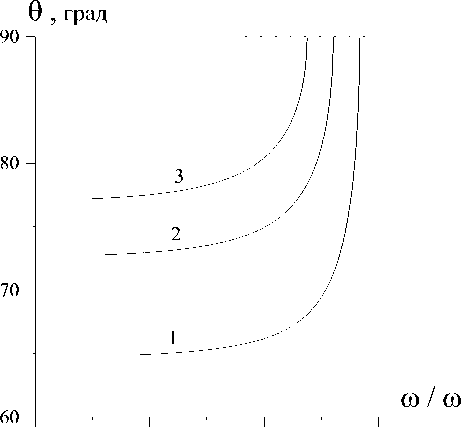
Угловые отклонения волновой нормали СПВ, вызванные движением ДГ, обычно невелики. Например, для точек минимума фазовой скорости на рис.3 они не превышают нескольких градусов. Однако в режиме околозвуковых движений ДГ угловое отклонение волновой нормали СПВ может оказаться значительным. Иллюстраций сказанному служит рис.4, где показаны частотные зависимости угла 0 для скоростей ДГ несколько меньших c_t . Для принятых скоростей ДГ величина 0 даже вдали от линии ФМР полей рассеяния превосходит 60⁰. С ростом частоты она дос-

0.0              0.3              0.6              0.9

Рис. 4. Частотные зависимости углового отклонения волновой нормали СПВ при X =0,01 и tom / to0 =0,01: 1 - VD /ct =0,9; 2 - VD /ct =0,95;

3 - V_D / c_t =0,97

тигает предельного уровня 0 = n /2 (штриховая горизонтальная линия) при to , которым соответствуют значения s = 0, k = 0 . Последнее указывает на полную делокализацию колебаний СПВ в условиях распространения ортогонально ДГ, когда из-за компланарности волнового фронта магнитные полюса не возникают и происходит расцепление волны с удерживающей границей. Подобный же случай расцепления электрозвуковой поверхностной волны с движущейся ДГ в сегнетоэлектрике отмечался в работе [4].

Работа выполнена по проекту А 0066 ФЦП "Интеграция".