Параметрическое самовозбуждение динамической системы резания
Автор: Заковоротный Вилор Лаврентьевич, Фам Тху Хыонг
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 5-6 (74) т.13, 2013 года.
Бесплатный доступ
Рассматривается проблема обеспечения устойчивости траекторий формообразующих движений инструмента относительно заготовки с учётом параметрического самовозбуждения. Анализируются факторы, вызывающие периодические изменения параметров в динамической системе резания. Они связаны с пространственной анизотропией свойств упругости в подсистеме обрабатываемой заготовки, с вариациями припуска по периметру вращения заготовки, с кинематическими возмущениями со стороны механической части приводов исполнительных элементов станка, с периодическими процессами в зоне резания. Приведена обобщённая динамическая модель системы с периодически изменяющимися параметрами. Выполнено изучение влияния периодически изменяющихся параметров на устойчивость траекторий. Раскрыты особенности потери устойчивости, специфические для динамических систем резания. В частности, показано, что за счёт параметрических эффектов по мере увеличения скорости резания при возрастании частоты вращения шпинделя всегда существует критическая частота, при которой система теряет устойчивость.
Устойчивость, периодическое изменение параметров, параметрическое самовозбуждение
Короткий адрес: https://sciup.org/14250014
IDR: 14250014 | УДК: 621.9:531.3 | DOI: 10.12737/1286
Текст научной статьи Параметрическое самовозбуждение динамической системы резания
Введение. Проблема обеспечения устойчивости траекторий формообразующих движений инструмента относительно заготовки является одной из самых важных при выборе технологических параметров и конструктивных особенностей подсистем инструмента и заготовки, взаимодействующих через процесс резания [1—3]. Существующие представления о потере устойчивости базируются на использовании в качестве математических моделей систем линейных или нелинейных дифференциальных уравнений динамики. Однако практика показывает, что существующие представления противоречат многим известным экспериментальным данным. Например, исходя из существующих представлений, по мере увеличения скорости резания запас устойчивости в системе должен возрастать. Однако практика показывает, что это справедливо при относительно малых частотах вращения шпинделя. При увеличении частоты до некоторой пороговой величины всегда наблюдается увеличение вибраций, свидетельствующих о потере устойчивости траекторий. В настоящей статье, основываясь на известных представлениях о динамической системе резания, рассматривается практически не анализируемый ранее вопрос о самовозбуждении системы за счёт периодического изменения параметров в математическом описании динамики системы.
Оснований для учёта переменности параметров в динамической системе резания множество. Во-первых, свойства упругости в подсистеме обрабатываемой детали не являются симметричными. Это связано, по крайней мере, с изменениями радиальной жёсткости детали, закреплённой, например, в трёхкулачковом патроне. Во-вторых, при обработке заготовки, имеющей периодические изменения припуска, параметры динамической характеристики процесса резания также являются периодически изменяющимися. В-третьих, траектории исполнительных элементов станка всегда являются периодически изменяющимися за счёт кинематических возмущений, зависящих от точности и конструктивных несовершенств механической части приводов. В-четвёртых, при обработке большинства материалов имеет место периодическое изменение сопротивления резанию, связанное с периодическим формированием поверхности скольжения в области первичной пластической деформации. Наконец, многие технологические режимы принципиально имеют периодические изменения параметров, например, процесс фрезерования. Все перечисленные факторы вызывают, по крайней мере, периодические изменения суммарной жёсткости в уравне- ниях взаимодействующих подсистем. В таких системах, как известно из теории колебаний, возможно параметрическое самовозбуждение системы, зависящее от частоты периодического изме- нения параметров.
Обобщённая математическая модель динамической системы резания как системы с периодическими изменениями параметров. Для изучения условий самовозбуждения динамической системы резания, параметры которой являются периодически изменяющимися функциями времени, необходимо рассмотреть обобщённую модель системы. Такая модель должна учитывать главные свойства системы, но не быть излишне сложной. Ограничимся случаем, когда рассматриваются периодические изменения элементов матрицы жёсткости. Кроме этого, примем во внимание гипотезы, используемые ранее при анализе динамики системы с постоянными параметрами [2]. Они включают три положения: силы, формируемые в зоне резания, пропорциональ- ны площади срезаемого слоя; они имеют неизменную ориентацию в пространстве, задаваемую угловыми коэффициентами хi, i = 1,2,3; модуль силы запаздывает по отношению к деформаци- онными смещениями инструмента относительно заготовки. Таким требованиям соответствует сле- дующая модель, рассматривающая динамику системы в вариациях относительно точки равновесия:
d2y dy dy dy m —+ h 1 + h -Z2 + h + l C 1 + 4 1 sin(Qit) y + dt2 1,1 dt 21 dt 3,1 dt [ 1,1 1,1 ( 1 )] 1
+ [^ 2 + 41,2 sin (^ t + 6 1,2 ) ] У 2 C 3,1 + PX i t p ,0 ( 1 + Msin ( « 2 t ) ) ] У 3 + PX 1 ^ p ,0 z 1 = 0
m dy + h 1,2 y + h 2,2 y + h 3,2 y + [ C 1,2 + Д1,2 sin ( Q1 t + 61,2 ) ] У 1 +
‘ + [ c 2,2 + 42,2 sin (^ t + 62,2 ) ] У 2 + [ c 3,1 + PX 2 t p ,0 ( 1 + M sin (^ t ) ) ] У 3 + РХ Д ,0 z 1 = 0
d2y dy dy dy m —43 + h , -+- + h, + h, -y- + c y + cy +
2 1,3 2,3 3,3 1,3 1 2,3 2
C 3,3 + PX 3 t p ,0 ( 1 + Msin ( ^ 2 t ) ) ] У 3 + PX 3 ^ p ,0 z 1 = 0;
dz
T1 -t+z1=y- где y = {y1,y2,y3}T — вектор упругих деформационных смещений инструмента в простран- стве, мм ; ρ — давление стружки на переднюю поверхность инструмента, параметр, зависящий от физико-механических свойств обрабатываемого материала, геометрии инструмента и технологических режимов, кГ мм2 ; Sp,0 , tp,0 — соответственно величины подачи и глубины резания, не учитывающие упругие деформационные смещения; m = [ms^ ]; s, k = 1,2,3; ms,k = 0, при: s * k, h = [hs,k ]; s, k = 1,2,3, c = [cs,k ]; s,k = 1,2,3 — соответственно матрицы инерционных, диссипативных и упругих коэффициентов (они являются симметричными и положительно определёнными); T1 — постоянная времени, моделирующая запаздывание вариаций модуля силы резания по отношению к деформационному смещению y1, с.
Таким образом, при установившемся состоянии в точке равновесия z 1 = y 1 = 0 . Кроме этого, в (1) учитывается пространственная анизотропия упругости системы в виде матрицы:
" 4 1,1 sin ( ^ 1 t ) 4 2,1 sin ( ^ 1 t + 6 2,1 ) 0 "
4 = 4 1,2 sin ( ^ 1 t + 6 1,2 ) 4 2,2 sin ( ^ 1 t + 6 2,2 ) 0 .
В (2) отсутствует переменная составляющая по направлению y 3 , так как кинематические возмущения по направлению оси вращения шпинделя формируются на основе следующего интегрального преобразования:
t
У3 = J v3 (t ) dt, t-T где v3 (t) — переменная составляющая скорости продольной подачи, мм/c .
Нетрудно показать, что в y 3 ( t ) все переменные составляющие, равные или кратные периоду вращения шпинделя T , равны нулю. Причём в (1) учитываются переменные составляющие, обусловленные вариациями координаты суппорта, в направлении, ортогональном к направлению его движения, а также вариации припуска, периодические с частотой вращения шпинделя
С р ( t ) = 0
PX l t p .Q ( 1 + Msin ( « 2 t ) ) PX 2 tp ,0 ( 1 + Msin ( « 2 t ) ) PX 3 tP ,0 ( 1 + Msin ( ^ 2 t ) )
В (1) частоты Ω1 и Ω2 равны или кратны частоте вращения шпинделя. Поэтому для анализа устойчивости системы (1) можно использовать теорию Флоке [4]. При изучении областей устойчивости использовался метод прямого цифрового интегрирования систем дифференциальных уравнений, основанный на методе Рунге — Кутты четвёртого порядка. Потеря устойчивости фиксировалась по траекториям решений дифференциальных уравнений.
Особенности параметрического самовозбуждения в динамической системе резания. Система (1) отличается от традиционно анализируемой системы следующими основными особенностями:
– в реальной динамической системе резания всегда имеет место изменение параметров, обусловленное различными причинами, поэтому, как правило, имеется несколько частотных составляющих изменения параметров, кратных частоте вращения шпинделя;
– вариации сил запаздывают по отношению к изменениям упругих деформационных смещений, причём запаздывание зависит как от технологических режимов, так и от геометрии инструмента и физико-механических свойств обрабатываемого материала. Поэтому даже без параметрических эффектов система может потерять устойчивость. Периодические же изменения параметров, как правило, дополнительно способствуют потере устойчивости;
– упругие свойства подсистемы заготовки без процесса резания являются линейными и матрицы упругости являются симметричными и положительно определёнными. Поэтому в пространстве для моделирования упругости можно на основе матрицы поворота выделить оси коллинеарного и ортогонального направлений, которые вращаются при повороте шпинделя при заданной анизотропии свойств упругости. Это обстоятельство может вызывать параметрическое самовозбуждение системы, которое дополняет условия самовозбуждения за счёт влияния циркуляционных сил, формируемых динамической связью процесса обработки.
Для дальнейшего анализа приведём некоторые характерные примеры параметрического самовозбуждения системы. Для этого рассмотрим различные диаграммы параметрического самовозбуждения в плоскости n = w/w0 - M, где ω0 — собственная частота основного колебательного контура системы, Гц; ω — частота параметрического возбуждения,Гц; m — уровень параметрического возбуждения (м < 1).
Для более наглядного выяснения влияния различных особенностей системы на потерю устойчивости, сначала рассмотрим скалярный аналог системы (1). Проанализируем для этого случая влияние двухчастотного параметрического возбуждения для системы:
m ddty + hdy + c ( 1 + p 1 sinto t + p 2 sin 3to t ) y = - cPz; dz
[Tdt+ z=y, где m, h, c — соответственно масса, коэффициент демпфирования и жёсткости подсистемы; сР — жёсткость процесса резания, кГ/мм ; T — постоянная времени стружкообразования, с.
Рассмотрим изменение области параметрического возбуждения системы на плоскости па раметров (p1, п) при варьировании р2 от нуля до 0,8 и при заданных значениях параметров ди- намической системы cP = 500кГ/мм, T = 0,1мс, h = 0,10кГ/мм. Соответствующие диаграммы параметрического возбуждения системы приведены на рис. 1. η
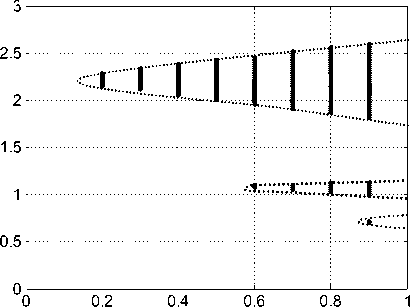
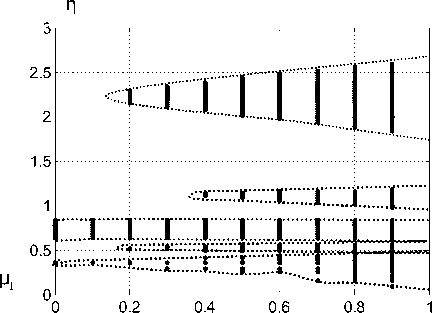
Рис. 1. Пример изменения области параметрического возбуждения системы на плоскости параметров ( p 1 , п )
для случаев р2 = 0,0 (левая диаграмма) и р2 = 0,8 (правая диаграмма)
Приведённый пример вычислен для системы, имеющей собственную частоту консервативной системы to0 = 150,0 с - 1. Если рассматривать частоту вращения шпинделя равную
3000 об/мин, то есть 50 Гц, то вторая диаграмма уже находится в области параметрического самовозбуждения системы. Однако, если рассматривается скалярный случай, то параметрическое самовозбуждение системы наблюдается при высоких частотах вращения шпинделя, характерных лишь для скоростного резания. Ситуация принципиально меняется, если анализировать векторный случай пространственных колебательных смещений.
Приведём пример условий параметрического самовозбуждения системы для случая, когда деформационные смещения инструмента происходят в плоскости. Линеаризованное уравнение в вариациях для этого случая имеет вид:
mddy1 + hdy + с • [1 + psin(tot + 81,1)]У1 + 2c • MSin(tot + 81,2)У2 = -X1cPz1, mdy2 + hdyL +1 c • psin(tot + 812)• У1 + c •[1 + psin(tot + 822)!У2 = —X^CpZ2,
J dt 2 dt 2 v , 7 L v ,
T z + z - = У 1 ,
T2 ^ + " 2 = У 1 , где c P = р SP .
В системе (5) дополнительно учитывается, что запаздывание сил по двум ортогональным направлениям отличается. Обратим внимание на то, что в системе (5) имеет место вращение угла ориентации эллипса жёсткости. Этот факт вызывает дополнительные условия параметрического самовозбуждения системы резания.
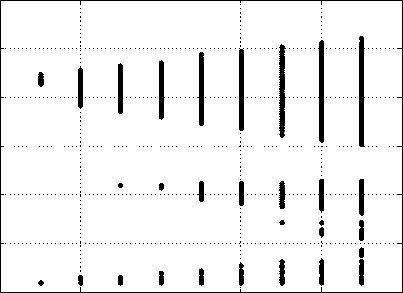
Рассмотрим конкретный пример (рис. 2). Исходные данные: матрица инерционных коэффициентов m = 5,63■ 10-4 кГ2/мм; матрица диссипативных коэффициентов h = 0,1 кГ/мм; матри ца жёсткости c = 2000 кГ/мм; cP = 500 кГ/мм; первая собственная частота системы w0 = 150Гц; вектор коэффициентов ориентации сил х = {х1,х2}T ={0,5; 0,8}T . Диаграмма построена по отношению к первой собственной частоте системы без резания. Угол ориентации эллипса жёсткости рассматривается при р = 0.
η
2.5
1.5
0.5
।
0.2
0.4
।________I
I
0.6
0.8
2.5
1.5
0.5
μ 0
η
0 0.2 0.4 0.6 0.8 1
Рис. 2. Изменение области параметрического возбуждения в плоскости ( п, р ) при варьировании угла ориентации эллипса жёсткости: a — а = 0 ° ; б — а = 45 °
Здесь большое значение в механизме самовозбуждения имеют условия обмена силовыми потоками между подсистемами, рассматривающими колебательные смещения в двух ортогональных направлениях в плоскости, нормальной к оси вращения шпинделя. Приведённые данные показывают, что в рассматриваемой системе параметрическое самовозбуждение наблюдается уже при частотах вращения шпинделя, равных (400,0—500,0) об/мин. Более скрупулёзный анализ показывает, что на условия самовозбуждения в этом случае оказывают влияние следующие факторы:
-
1) Известно [2], что за счёт реакции со стороны процесса обработки суммарная матрица упругости становится несимметричной. Поэтому без параметрических эффектов (р = 0) в системе естественным образом формируются циркуляционные силы. В зависимости от направления действия циркуляционных сил (сил, ортогональных к направлению деформационных смещений) и направления вращения эллипса жёсткости могут формироваться условия, способствующие самовозбуждению, или направленные на стабилизацию равновесия.
-
2) Рассматриваемая система имеет две резонансные частоты, которые разделены в частотной области антирезонансом. При сближении этих частот в системе формируются формы колебаний типа биений с частотой, равной разности резонансных частот. В результате может существенно снижаться частота вращения шпинделя, при которой наблюдается эффект параметрического самовозбуждения.
Аналогичный эффект наблюдается и в том случае, когда в динамической системе резания рассматривается влияние двух физических процессов, вызывающих изменения параметров. Как и ранее, рассмотрим пример (рис. 3). В этом примере в отличие от (5) матрица жёсткости равна c = с
[ 1 + M i sin ( w t + 0 1,1 ) + м 2 sin ( W 2 1 + 9 1,1 ) ] 2 [ M i sin ( w t + 0i,2 ) + М 2 sin ( м 2 t Ur ) ]
2 [ M i sin ( W t + 02,i ) + М 2 sin ( W t + 9 i,2 ) ] [ 1 + M i sin ( wi t + 0 2,2 ) + м 2 sin ( W t + 9^ 2 ) ]
ω
Здесь удобно ввести в рассмотрение коэффициент к = —, изменение которого определяет со- ω ω1
отношение частот параметрического возбуждения. Приведённые на иллюстрации данные получены при м2 = 0,5. На приведённых иллюстрациях не показана высокочастотная область, как наименее интересная для рассматриваемых прикладных задач.
2.5
1.5
0.5
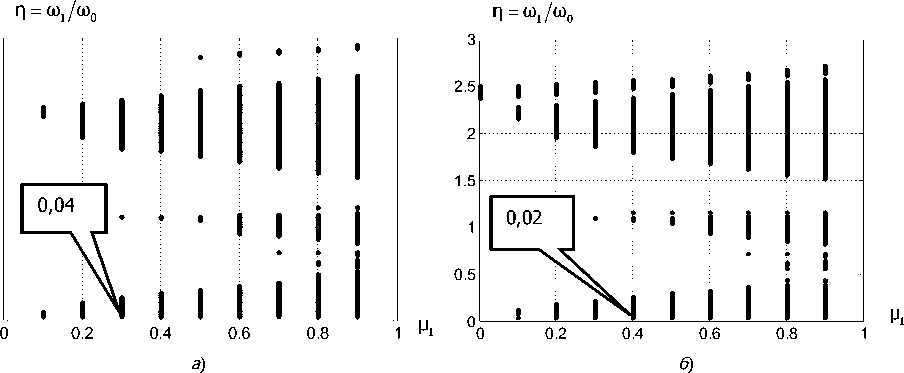
Рис. 3. Изменение области параметрического возбуждения в плоскости ( n, Mi ) при варьировании частотного отношения k = Ш2 : а — к = 0,2 ; б — к = 0,9 ω ω1 ω ω
Здесь также обнаруживается существенное снижение нижней частоты вращения шпинделя, при которой наблюдается параметрическое самовозбуждение системы, по мере сближения частот параметрического возбуждения. В реальной динамической системе резания, имеющей большее число степеней свободы и условий, вызывающих периодические изменения параметров, картина параметрического самовозбуждения существенно расширяется.
Заключение. Параметрические эффекты в динамической системе резания играют заметную роль в формировании области устойчивости траекторий формообразующих движений. Если следовать традиционному представлению о повышении устойчивости, то по мере увеличения скорости резания, связанной с возрастанием частоты вращения шпинделя, область устойчивости должна расширяться. На практике это не соответствует данным экспериментов. По мере увеличения частоты вращения шпинделя, начиная с некоторого её критического значения, система вновь теряет устойчивость. Это обусловлено параметрическим самовозбуждением. Поэтому в зависимости от состояния станка, вызывающего кинематические возмущения траекторий, и его конструктивных особенностей, по мере увеличения скорости резания существует ограниченный частотный диапазон вращения шпинделя, при котором в низкочастотной области теряется устойчивость процесса резания за счёт влияния, прежде всего, запаздывающих аргументов. В высокочастотной области устойчивость вновь теряется за счёт параметрического самовозбуждения системы.
Список литературы Параметрическое самовозбуждение динамической системы резания
- Кудинов, В. А. Динамика станков/В. А. Кудинов. -Москва: Машиностроение, 1967. -367 с.
- Заковоротный, В. Л. Динамика процесса резания. Синергетический подход/В. Л. Заковоротный, М. Б. Флек. -Ростов-на-Дону: Терра, 2006. -876 с.
- Заковоротный, В. Л. Системный синергетический синтез управления динамикой металлорежущих станков с учётом эволюции связей/В. Л. Заковоротный [и др.]. -Ростов-на-Дону: Изд. центр Дон. гос. техн. ун-та, 2008. -324 с.
- Хартман, Ф. Обыкновенные дифференциальные уравнения/Ф. Хартман. -Москва: Мир, 1970. -720 с.


