Параметризация моделей управляемых систем

В классической теории управления [1] обычно используются параметрические модели, которые строятся в условиях параметрической неопределенности. Здесь предполагается известным факт принадлежности модели к некоторому заранее определенному конечномерному классу моделей. Процедура идентификации (оценивания) модели сводится при этом к оцениванию по данным наблюдений некоторого конечного набора параметров.

Столь полную априорную информацию можно считать доступной далеко не всегда, поэтому параллельно развивается и непараметрическая теория управления [2; 3], в которой априорный класс моделей предполагается бесконечномерным; при этом говорят о непараметрической неопределенности. Малое количество априорной информации приходится компенсировать при этом большим количеством статистических наблюдений.

Основными строительными блоками для создания математических моделей систем управления по наблюдениям являются оценки плотности распределения и функции регрессии [1–3]. Непараметрическая оценка плотности распределения ядерного типа была впервые рассмотрена в [4; 5], а соответствующая непараметрическая оценка функции регрессии – в работах [6; 7].

Классические параметрические оценки этих функций гораздо проще для человеческого восприятия и лучше приспособлены для анализа, чем непараметрические оценки. Поэтому постоянно предпринимаются попытки построения оценок параметрического вида в условиях непараметрической неопределенности. Это направление можно назвать параметризацией моделей.

Одной из ветвей этого направления является использование оценок в виде отрезков ортогональных рядов, называемых еще проекционными оценками ввиду прозрачной геометрической аналогии. Оценка такого типа для плотности распределения была предложена Н. Н. Ченцовым в [8], а оценка для функции регрессии – в [9].

Проекционные оценки были подвергнуты тщательному изучению. Так, в статьях [10–13] исследовались вопросы сходимости оценок в различных смыслах, в публикациях [14; 15] проводилось сравнение различных непараметрических оценок. В [16–19] исследовались проекционные оценки в конкретных базисах. Во всех этих исследованиях длина отрезка ортогонального ряда выбиралась произвольно. В работах [20–24] предложен некий принцип оптимального выбора длины отрезка ортогонального ряда в проекционных оценках, исследованы свойства получаемых оптимальных проекционных оценок. В настоящей работе приведен обзор результатов [20–24], и представлены соображения по поводу обобщения оптимальных проекционных оценок на многомерный случай.

Проекционное приближение. Пусть Lr2 – гильбертово пространство функций f, заданных на подмножестве U вещественной оси и интегрируемых с квадратом с весом r в смысле f f 2(x)r (x)dx <”,

U где r – неотрицательная весовая функция на U. Скалярное произведение и норма задаются в Lr2 выражениями:

⁽ f , g ) = J f ⁽ x ) g ⁽ x) r ⁽ x ) dx , Il f 11= V ⁽ f , f ).

U

Любая функция f из L r ² представима в виде ряда [25]

f (x) = 2 ajgj( x), j■=0

в смысле сходимости последовательности его частич- ных сумм

N fN (x ) = 2ajgj( x )

j = 0

по норме пространства L_r 2 , что означает || f - f_N\\ ^ 0 при N ^ -а Здесь G = { g j , j = 0, 1, ...} обозначена произвольная полная ортонормированная система в L r ² , а a j = ( f , g j ), j = 0, 1, … представляют собой коэффициенты Фурье функции f относительно системы G .

Выбор ортонормированной системы G зависит от конкретной задачи; в различных ситуациях могут быть использованы, например, классические ортогональные многочлены [26] или тригонометрическая система функций [27].

Оценка плотности распределения. Пусть X , X ₁, …, X_n , … – последовательность независимых, одинаково распределенных на U с R случайных величин, и пусть распределение X имеет неизвестную плотность f . Рассмотрим задачу оценивания неизвестной плотности распределения f по выборке наблюдений X ₁, …, X_n объема n в ситуации, когда априори неизвестен какой-либо конечномерный класс плотностей, которому заведомо принадлежит f , т. е. в ситуации непараметрической неопределенности.

В [4; 5] для этого была предложена ядерная оценка плотности f            ГxXL)

fn. h (x)     , 2K I L I nh'=i   1 h 7            (2)

1 ⁿ

=-2 Kh (x - XD, xe U, n i=i где K – некоторая плотность распределения на R, называемая ядром оценки, Kh(u) = K(u/h)/h; h – параметр оценки, называемый параметром размытости или параметром ширины окна.

В [8] рассматривалась проекционная оценка плотности, основанная на отрезке ряда (1), в котором коэффициенты Фурье a j заменены на оценки по выборке наблюдений вида

n aj = - 2 gj( Xi) r (Xi), j = 0,1, -n i=i

Таким образом, проекционная оценка плотности имеет вид

N

• f , N ⁽ x ) = 2 ^{a l}j g j⁽ x ), x ^e U .           ⁽³⁾

j = 0

Отметим, что в результате несложных преобразований эту оценку можно представить следующим образом:

n f., N (x) = - 2 Kn (x, Xi), n i=i

N

K n ( x , u ) = 2 g j ( x ) g j ( u ) r ( x ), x , u ^e U .

j = 0

Это представление по виду напоминает второе представление в оценке (2), как среднее выборочное значение некоторого ядра. Существенное отличие состоит в том, что ядро в последнем выражении не является плотностью распределения, в частности, оно может принимать отрицательные значения. Таким же недостатком обладает и проекционная оценка (3), она не является, вообще говоря, плотностью распределения, поскольку может принимать отрицательные значения. В некоторых случаях избавиться от этого недостатка позволяет следующий прием. В качестве оценки плотности рассматривается среднее арифметическое первых частичных сумм ряда

N fn,n (x)=iftt2 fn,j(x), x e U.

^N + ¹ j = 0

Такой прием позволяет обеспечить неотрицательность оценки плотности, например, при использовании тригонометрической ортонормированной системы [27]. При этом оценка оказывается построенной посредством так называемых сумм Фейера [27].

Длина разложения N выбирается в [8] произвольно, там также приводятся некоторые асимптотические соображения по поводу выбора N . В работах [20–22; 24] предложен и исследован оптимальный принцип выбора длины отрезка ряда, основанный на следующем наблюдении. Обозначим t j = g j ( X ) r ( X ), j = 0, 1, … и вычислим среднеквадратичное отклонение проекционной оценки плотности (3) от неизвестной плотности f . Получаем выражение

2    ^NN

T n (^N ) = Sf - Ц =1 f Г - ⁿT 2 a 22+ - 2 Et 2,- (4)

ⁿ j = 0       ⁿ j = 0

Оказывается [20; 24], что величина T n ( N ) при фиксированном n достигает минимума по N , это означает, что при любом объеме выборки имеется оптимальная длина отрезка ряда в проекционной оценке (3), причем оптимальность понимается в смысле среднеквадратического критерия (4). Для приближенной минимизации критерия (4) с использованием выборки наблюдений заметим [20; 24], что слагаемое ║f║ в правой части (4) не влияет на положение точки минимума, и его можно отбросить, а остальные члены оцениваются следующим образом:

~ _n n + 1 ^ a 2   2 N -

T n ( N ) =-- 2 a 2 +- 2 1

n    j = 0        n j = 0

~”

j ,

n tj=12 g j( X) r ^( X).

n t1

Минимизация Tˆn (N) по N дает оптимальное значение Nˆ длины отрезка ряда, подстановка которого в выражение (4) дает оптимальную проекционную оценку ■ N f (x)=Zajgj(x), xe U.          (6)

j = 0

В качестве примера рассмотрим тригонометрическую ортонормированную систему на [–1; 1], которая состоит из функций j 2,sin(njx ),cos(njx), x e [-1; 1], j = 1,2, „.j.

При использовании этой ортонормированной системы удобно включать члены в ортогональное разложение парами, при этом оптимальная проекционная оценка приобретает вид

• 1    N ^ˆ

f(x) = + Z(Cjcos(njx) + S/sinm/x))-

• ²    j = i

Здесь

1n1

Cj = - Z cos( n /X i ), ^v      Z sin( n /X i ), j = 1, 2, —

П i=1

Рассмотрим случайную величину X , имеющую распределение с треугольной плотностью на [–1; 1], т- е- fx ) = 1- |x| , x e [ - 1;1]- Методами статистического моделирования нетрудно получить выборку наблюдений такой случайной величины, для целей иллюстрации мы возьмем объем выборки равным n = 50. График оценки критериальной функции (5), построенный по полученной выборке, приведен на рис. 1. Видно, что в оптимальное разложение входит только первая пара тригонометрических функций ( N = 1). Графики модельной плотности распределения f и ее оптимальной проекционной оценки показаны на рис. 2. С ростом объема выборки качество оценивания довольно быстро возрастает. Более подробный анализ оптимальных проекционных оценок плотности можно найти в работах [20–24].

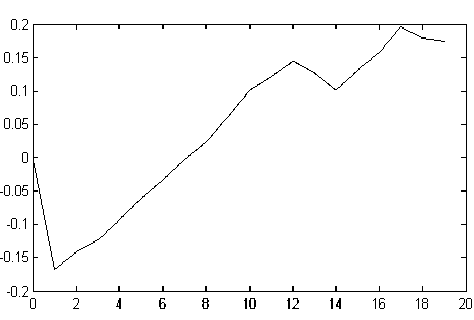
Рис. 1. График оценки критериальной функции (5), построенный по выборке наблюдений объема n = 50

Оценка функции регрессии. Пусть теперь (X, Y), (X1, Y1), …, (Xn, Yn), … – последовательность незави- симых одинаково распределенных случайных векторов. Обозначимfx) = E(Y\X = x), x e U функцию регрессии Y на X. Для непараметрического оценивания этой функции по наблюдениям (Xi, Yi), i = 1, …, n в [6; 7] была предложена ядерная оценка

— 'Zy^K I x—Xi-nh и I h

f ^{( x} ) =

1 5 f x - X,) , z K I I

nh        h i=1

x e U .

Здесь объекты K , h имеют тот же смысл, что и для ядерной оценки плотности (2).

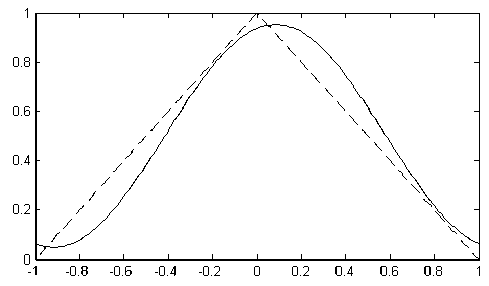
Рис. 2. График модельной треугольной плотности распределения и ее оптимальной проекционной оценки (7), объем выборки n = 50

Для простоты предположим, что U = [0; 1] и случайная величина X имеет равномерное распределение на [0; 1] так, что ее плотность равна P(x) = 1, x e [0; 1]. Положим также, что весовая функция постоянна: r(x) = 1, x e[0;1]. При этом коэффициенты Фурье имеют вид aj = j f (x)gy(x)dx = E(Ygj(X)), j = 0, 1, ^ 0

Поэтому проекционная оценка функции регрессии имеет вид (3), где оценки коэффициентов Фурье вычисляются по формулам:

n aj= - Z Yg( X,), j = 0,1, -n ,=1

Все свойства критерия выбора длины ортогонального разложения сохраняются и в случае оценивания функции регрессии, оптимальная проекционная оценка вычисляется по той же формуле (6), а качество приближения получается даже лучше, чем для плотности распределения, что связано со спецификой данной задачи.

Случай известной, но не равномерной плотности распределения X отличается лишь повышенной громоздкостью формулировок. В случае неизвестной плотности X можно использовать фейеровские оценки [23; 24].

Многомерное обобщение. Представляет интерес обобщение описанных оценок на многомерный случай, когда область распределения случайной величи- ны X имеет размерность, превышающую 1. Для осуществления такого обобщения по существу нужно лишь уметь строить многомерные ортонормирован-ные системы. Это легко достигается на основе одномерных ортонормированных систем, что мы и продемонстрируем для двумерного случая.

Пусть { g j (x ), j = 0, 1, ■■■}> x e U и { h k (y ), k = 0, 1, ...}, y e V - одномерные полные ортонормированные системы на соответствующих областях определения. Тогда полная ортонормированная система на U × V образуется из всевозможных произведений одномерных функций, а именно:

Gjk( x, y ) = gj( X) hk (y), j = 0,1, ^, k = 0,1, _,(x, y) e U X V.

Следует иметь в виду, что с ростом размерности очень быстро нарастают комбинаторные сложности в вычислении ортонормированных функций, поэтому применимость описанного способа оценивания в пространствах высокой размерности сомнительна. Кроме того, метод проекционного оценивания не обладает свойствами локальных оценок, вследствие чего не может использовать «трубчатое» строение выборочных данных. По-видимому, возможно построение специальных ортонормированных систем, адаптированных под имеющуюся структуру данных, что позволит использовать такое специальное строение, однако, нам неизвестны исследования в этом направлении.

В работе дан краткий обзор оптимальных проекционных оценок плотности распределения и функции регрессии, которые применяются при построении моделей управляемых систем по наблюдениям. Описаны основные алгоритмы, участвующие в построении оценок, приведены примеры и иллюстрации. Отмечается возможность многомерного обобщения процедуры оценивания и имеющиеся ограничения по размерности.