Параметризация нелинейного предсказателя Грехэма при компрессии цифровых изображений

Все методы компрессии на основе дифференциальной импульсно-кодовой модуляции (ДИКМ) [1–5] так или иначе эксплуатируют идею кодирования разностного сигнала (изображения) вместо исходного. Разностный сигнал вычисляется вычитанием из каждого отсчета исходного сигнала некоторого предсказанного значения. Переход к разностному представлению декоррелирует сигнал, что приводит к повышению эффективности его компрессии.

Несмотря на простоту лежащей в основе идеи, ДИКМ обладает существенными преимуществами, наиболее важными среди которых является низкая вычислительная сложность и возможность обеспечения постоянной скорости формирования выходного потока сжатых данных. Благодаря этому ДИКМ по-прежнему перспективен при компрессии данных дистанционного зондирования Земли [6–9], в геоин-формационных системах [10–12], а также включен в качестве одного из этапов в другие методы компрессии цифровых изображений, например JPEG [13].

Важным этапом ДИКМ является предсказатель, точность и скорость которого оказывают существенное влияние на эффективность метода в целом. При этом для предсказания в ДИКМ чаще всего используются тривиальные схемы, основанные на простом усреднении по ближайшим пикселам изображения. Причиной этого является желание сохранить на достаточно низком уровне вычислительную сложность компрессии. В этой ситуации актуальной является задача разработки предсказателей, позволяющих повысить эффективность компрессии при сохранении вычислительной сложности на приемлемом уровне.

В данной работе предлагается адаптивный предсказатель, который позволяет повысить эффективность метода ДИКМ за счет использования различных способов предсказания для каждого пиксела изображения в зависимости от направления контура в окрестности этого пиксела.

Работа построена следующим образом. В первом пункте приведено краткое описание общей схемы метода компрессии цифрового изображения на основе ДИКМ. Во втором пункте рассмотрено предсказание для ДИКМ и описано построение адаптивного параметризованного предсказателя. В третьем пункте описана процедура обучения адаптивного предсказателя. В четвёртом пункте кратко рассмотрены способы квантования в ДИКМ. В пятом пункте приведены результаты вычислительных экспериментов на реальных изображениях.

1.    Дифференциальная импульсно-кодовая модуляция при компрессии изображений

Рассмотрим процедуру компрессии изображения на основе ДИКМ. Пусть x ( m , n ) – отсчеты исходного цифрового изображения (для простоты изложения целочисленные неотрицательные), которое подвергается компрессии, а x ( m, n ) - отсчеты декомпрессированного (восстановленного после компрессии) изображения. При компрессии изображение обрабатывается построчно. При этом для каждого отсчета на основе уже прошедших компрессию и восстановление отсчетов вычисляется предсказанное значение

5 ( m , n ) = P { x ( i , j ) : i <  m or i = m and j <  n } , (1)

где P – функция предсказания, которая работает на основе восстановленных отсчётов x (m, n) для обеспечения идентичности предсказания на этапах компрессии и декомпрессии. Затем предсказанное значение вычитается из исходного для получения разностного сигнала f (m,n) = x(m,n)-x(m,n) ,                      (2)

который подвергается квантованию f (m,n)= Q(f (m,n)) ,                           (3)

где Q - функция квантования, a f (m, n) - квантованный разностный сигнал, который упаковывается в канал связи либо архивный файл. Затем производится восстановление текущего отсчета x (m, n ) = f (m, n) + x (m, n) .                      (4)

Восстановленный отсчет используется для предсказания (1) следующего отсчета.

Процедура декомпрессии на основе ДИКМ принимает на вход распакованный из канала связи или архивного файла квантованный разностный сигнал f ( m , n ) и состоит из шагов предсказания (1) и восстановления (4).

• 2.    Предсказание при компрессии изображений на основе ДИКМ

В целях уменьшения вычислительной сложности в ДИКМ обычно используются очень простые предсказатели [14], использующие только ближайшие к предсказываемому отсчёты изображения. Рассмотрим примеры таких предсказателей и пронумеруем их:

x ⁽⁰⁾ ( m , n ) = x ( m - 1, n ) ,                             (5)

x ⁽¹⁾ ( m , n ) = ( x ( m - 1, n ) + x ( m , n - 1 ) )/2 ,          (6)

x ^<2) ( m , n ) = x ( m , n - 1 ) .

Рассмотренные предсказатели линейны и поэтому обязательно будут ошибаться на контурах. Под контуром здесь понимается пространственно протяжённый перепад яркости, не обязательно замкнутый (граница между однородными фрагментами изображения). Для сокращения ошибки предсказания на контурах обычно используются нелинейные схемы, например предсказатель Грехэма [15]:

x G ( m , n ) =

x ⁽⁰⁾ ( m , n ) , if % m ( m , n ) <% _n ( m , n ); x² ( m , n ) , if % m ( m , n ) >% n ( m , n ),

где

% _m ( m , n ) = x ( m , n - 1 ) - x ( m - 1, n - 1 ) ,          (9)

% _n ( m , n ) = x ( m - 1, n ) - x ( m - 1, n - 1 ) .         (10)

Сравнение разностей (9) и (10), соответствующих жирным линиям на рис. 1, используется для опреде- ления направления контура в окрестности текущего отсчета, а выражение (8) обеспечивает предсказание «вдоль» контура, т.е. вдоль той стрелки на рис. 1, которой соответствует меньшая из разностей (9–10).

Такой предсказатель, в отличие от усредняющей схемы (6), точнее работает на контурах, но менее точен на относительно ровных участках, где ему мешают шумы. Другими словами, погрешность предсказания (2) нелинейной схемы (8) на контурах меньше, чем погрешность усредняющей схемы (6) за счёт того, что нелинейная схема использует соседние точки контура с близкой яркостью, а не точки соседних однородных областей, яркость которых может заметно отличаться. С другой стороны, линейная схема (6) более точна на ровных участках, т.к. влияние шума при использовании этой схемы уменьшается за счёт усреднения по соседним отсчётам.

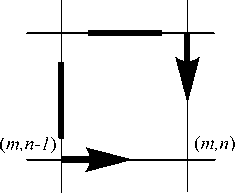
Рис. 1. Предсказатель Грехэма для ДИКМ

В данной работе предлагается адаптивный предсказатель, совмещающий преимущества «усредняющего» предсказателя (6) и предсказателя Грехэма (8) за счет автоматического переключения между ними в каждой точке изображения. Идея предсказателя, который работает похожим образом, была предложена в [16] для другого метода сжатия, основанного на

X1"1                  X,+)                    X

Рис. 2. Адаптивный предсказатель для ДИКМ

В данной работе произведена модификация этого предсказателя для его использования в методе ДИКМ, результатом которой является предлагаемый адаптивный предсказатель:

x ⁽⁰⁾ ( m , n ) , if % ( m , n ) <% ^{( - )};

:xA ( m , n ) = <  x ⁽¹⁾ ( m , n ) , if % ^{( - )} < % ( m , n ) <% ⁽⁺⁾; (11) x ⁽²⁾ ( m , n ) , if % ^{( + )} <% ( m , n ),

где «признак контура» % ( m , n ) вычисляется следующим образом:

% ( m , n ) = % m ( m , n ) -% n ( m , n ) ,                  (12)

а % ( ^{- )}, % ^{( + )} - пороги переключения, удовлетворяющие условию:

- x max <% ( ^{- )} <  0 <% ( ^{+ )} <  x max ,                   (13)

где [ 0, x max ] - диапазон возможных значений яркости изображения.

Нетрудно видеть, что предсказатель (11) также можно рассматривать как параметризацию предсказателя Грехэма (8). При этом знак «признака контура» A ( m , n ) характеризует направление, а его модуль характеризует степень выраженности контура в точке ( m , n ). При этом A⁽⁺⁾ , A^{( 1} задают пороги переключения между предсказателем Грехэма и усредняющим предсказателем (6). Если в текущей точке есть достаточно выраженный контур, то будет использовано предсказание «вдоль контура» (с учетом направления), если же сильно выраженного контура нет, то произойдет усреднение по двум ближайшим уже обработанным отсчетам. Пороги A⁽⁺⁾ , A^{( 1} вычисляются автоматически процедурой обучения и перед собственно процедурой компрессии (один раз для изображения), что позволяет алгоритму адаптироваться к особенностям каждого конкретного изображения. Вычисленные при компрессии пороги A⁽⁺⁾ , A^{( 1} упаковываются в архивный файл (или канал связи) и затем используются при декомпрессии.

• 3.    Обучение адаптивного предсказателя при ДИКМ-компрессии изображений

Т.к. предсказатель должен работать как можно точнее, то подбор параметров предсказателя A⁽⁺⁾ , A^{( 1} можно производить исходя из минимизации суммы модулей погрешности предсказания:

8(A(+),A(-))= Z |x(m,n)-x(m,n)|^min.), (14) (m, n )еш                                        ’ где и - множество координат всех отсчётов изображения. Введём также в рассмотрение множества И(+), ш( ', ш(01 координат отсчётов изображения, для которых значение признака контура (12) положительно, отрицательно и равно нулю соответственно. Тогда погрешность предсказания, вычисленная по отсчётам, для которых признак контура (12) положителен, можно записать следующим образом:

8 ^{( +} ) ( A ^{( + )} ) = Z | x ( m , n ) - x ( m , n )| .            (15)

( m , n ) =to ^{( +} )

Нетрудно видеть, что эта погрешность зависит от положительного порога A⁽ ' ¹ и не зависит от отрицательного порога A^(-) . Аналогичным образом можно записать погрешности предсказания 8 * * (?J ) ), 8⁽⁰⁾ по отсчетам с отрицательным и нулевым значением признака (12) соответственно, при этом 8⁽ ) ( А⁽ ) ) зависит от только отрицательного порога A^(-) , а 8⁽⁰⁾ вообще от порога не зависит. Во введенных обозначениях погрешность предсказания может быть представлена в виде:

8 ( A ^{( + )}, A ^{( - )} ) = 8 ^{( - )} ( A ^{( - )} ) + 8 ⁽⁰⁾ + 8 ^{( + )} ( A ^{( +} ) ) .         (16)

Такое представление позволяет факторизовать двумерную задачу оптимизации (14) на две одномерных задачи:

A ^{( + )} = arg min 8 ^{( + )} ( A ) ,                           (17)

A ^{( - )} = arg min 8 ^{( - )} ( A ) . (18)

Рассмотрим решение задачи (17). Для этого понадобится предварительный проход по изображению (обучение предсказателя), при котором заполняется матрица

A i , a = Z x ( m , n ) - x ⁽ i ) ( m , n )| , (19)

( m , n ) e« ( A )

содержащая суммарные значения погрешности предсказания интерполятора номер i (5–7) для всех отсчётов, для которых значение признака (12) равно А . Диапазоны изменения индексов матрицы:

0 <  i <  2, - x max <А< x max . (20)

После заполнения этой матрицы одномерный массив значений погрешности (15) можно заполнить с помощью рекуррентной схемы xmax

⁸ ( ^{+ )} ( x _X ) = Z A ,„., , (21)

A=0

8 ^{( + )} ( A ) = 8 ^{( + )} ( A + 1 ) + A_2A-A _{1i X} ,0 x max , (22) вычислительная сложность которой не зависит от размера изображения.

Этот массив имеет длину всего ( x max +1), и оптимальное значение A⁽⁺⁾ может быть найдено в таком массиве простым перебором. На этом решение задачи (17) закончено. Задача (18) решается аналогично, с использованием того же самого предварительного прохода по изображению (второй предварительный проход не понадобится). В результате задача обучения адаптивного предсказателя будет решена, т.е. будут найдены пороги переключения A⁽⁺⁾ , А^(-) .

Таким образом, для каждого пиксела изображения вычисляются два из трех предсказанных значения (5– 7) и признак (12), а также заполняются два элемента матрицы (19). Кроме того, после первого прохода по изображению дважды запускается рекуррентная схема (21–22). Вычислительная сложность такого расчёта для изображения размера M × N составляет

U = 9 + (6 x max IM^N^ ) (23) аддитивных операций на отсчёт (в предположении, что деление на два и вычисление модуля не требует арифметических операций), причём вклад рекуррентной схемы, как правило, пренебрежимо мал. Так, для изображения размером 500×500 с диапазоном яркостей [0…255] вычислительная сложность составит 9,00612 операций на отсчёт, что приемлемо для большинства практических приложений.

• 4.    Квантование при компрессии изображений на основе ДИКМ

Для квантования в ДИКМ обычно используется шкала Макса [1–3]. Использование этой шкалы обеспечивает минимум относительной квадратичной погрешности отн

£ 2

D x

—1— z ( x ^{( m} , ^{n ) -} x ^{( m} , ⁿ ) ) 2,   ⁽²⁴⁾

MNDx (m,n)ew между исходным изображением x(m, n) и декомпрессированным изображением x (m, n) при фиксированном количестве уровней квантования (здесь Dx – оценка дисперсии исходного изображения).

Общая схема ДИКМ позволяет использовать также другие шкалы квантования, например равномерную шкалу, которая позволяет контролировать максимальную погрешность emax = max x (m, n)- x (m, n) . (25) (m, n )еш

Этот показатель используется в областях, где необходим более строгий контроль погрешности [17] из-за повышенных требований к качеству данных или уникальности этих данных, например при работе с данными дистанционного зондирования Земли, в том числе при компрессии гиперспектральных изображений [18–23].

Предварительные эксперименты, проведенные на Ватерлоо-наборе [24] изображений (типичные результаты см. на рис. 3–4), показали, что выбор шкалы квантования имеет важное значение, т.к. использование рассмотренных шкал приводит к существенно различающимся результатам.

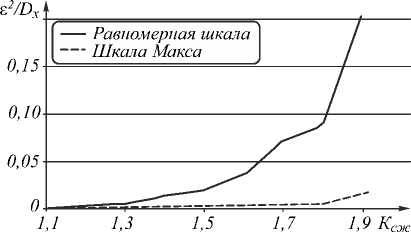
Рис. 3. Зависимость относительной квадратичной погрешности от коэффициента сжатия для ДИКМ

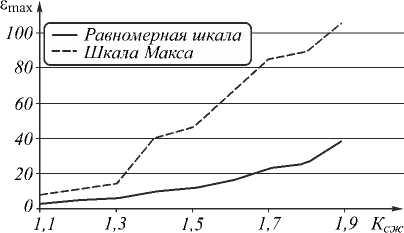
Рис. 4. Зависимость максимальной погрешности от коэффициента сжатия для ДИКМ

5.    Экспериментальное исследование предсказателей при компрессии изображений на основе ДИКМ

Вычислительные эксперименты проводились на полутоновой версии Ватерлоо-набора [24] изображений, который часто используется при сравнении методов сжатия цифровых изображений.

Сравнение производилось в координатах «по-грешность/коэффициент сжатия», при этом использовались показатели относительной квадратичной погрешности (24) и максимальной погрешности (25). Компрессия и декомпрессия производилась для всех изображений Ватерлоо-набора, после чего полученные результаты усреднялись.

На рис. 5 показана зависимость относительной квадратичной погрешности от коэффициента сжатия для ДИКМ при использовании квантователя со шкалой Макса для предсказателей по двум отсчётам (6), предсказателя Грехэма (8) и адаптивного предсказателя (11). Как видно из графика, адаптивный предсказатель имеет выигрыш по погрешности до двух раз

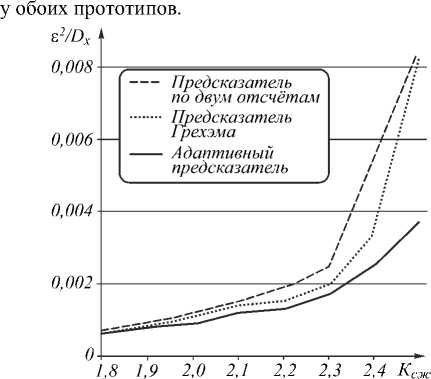
Рис. 5. Сравнение предсказателей для ДИКМ

Кроме того, в рамках данной работы ДИКМ с адаптивным предсказателем и равномерным квантователем сравнивался с методом компрессии JPEG. На рис. 6 показана зависимость максимальной погрешности от коэффициента сжатия для этого случая.

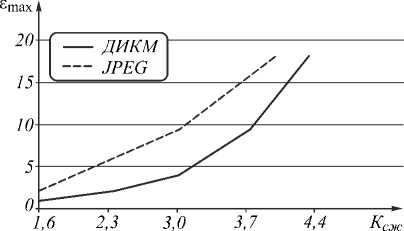
Рис. 6. Сравнение ДИКМ (с адаптивным предсказателем) с методом компрессии JPEG

Из графика видно, что ДИКМ с адаптивным предсказателем имеет заметный выигрыш по погрешности (до 2,5 раз). Так как JPEG во многих областях используется в качестве «очевидного и стандартного» решения (некоторые варианты JPEG применяются даже при бортовой компрессии), то полученные результаты позволяют сделать вывод о перспективности использования метода ДИКМ с предложенным адаптивным предсказателем.

Выводы

В данной работе был предложен адаптивный параметризованный алгоритм предсказания для метода компрессии ДИКМ, основанный на использовании различноых способов предсказания в зависимости от локальных особенностей изображения. Параметры предсказателя автоматически настраиваются на каждое изображение с помощью быстрой процедуры обучения. Проведённые исследования показали повышенную эффективность предложенного предсказателя по сравнению с прототипами.

В дальнейшем планируется исследование возможности отказа от предварительного прохода по изображению при обучении адаптивного предсказателя. При этом накопление статистики по погрешности различных вариантов предсказателя можно вести одновременно с собственно предсказанием, а модификацию порогов переключения можно производить исходя из статистики, накопленной к текущему моменту. Такая схема обработки сделает метод более удобным для систем реального времени.

Работа выполнена за счет гранта Российского научного фонда (проект №14-31-00014) «Создание лаборатории прорывных технологий дистанционного зондирования Земли».