Параметризация сейш для одномерной модели водоёма

Одномерные по вертикали модели водоёма, широко используются в различных задачах гидрологии, метеорологии и климатологии. Причиной этому является их вычислительная простота, и в целом успешные результаты воспроизведения теплового режима, и биогеохимических характеристик озёр. Для многих задач важно формирование в модели правильных вертикальных распределений термодинамических и биогеохимических переменных, которые определяются, особенно в период открытой воды, турбулентным перемешиванием.

«Московский физико-технический институт (государственный университет)», 2018

Турбулентное перемешивание, в свою очередв, связано с полем течений; это поле в одномерных моделях, как правило, рассчитывается в приближении горизонтального пограничного слоя с вращением [1], что справедливо только для водоёмов с горизонтальными размерами, сильно превышающими внутренний радиус деформации Россби Lr (Lr ~ 2 — 3 км для умеренных широт). Для малых водоёмов сила Кориолиса становится пренебрежимой в сравнении с силой горизонтального градиента давления, вызванного распределением массы в озере. Взаимодействие перераспределения массы и градиента давления приводит в замкнутых водоёмах к гравитационным колебаниям, известным как сейши. Поскольку горизонтальный градиент давления почти во всех в одномерных моделях не учитывается, не воспроизводятся и сейши.

Сейши обуславливают в водоёмах спектр флуктуаций всех термогидродинамических величин, с максимальными амплитудами в термоклине, однако влияние этих колебаний на среднюю стратификацию исследовано к настоящему времени слабо. Предложено множество моделей, построенных для воспроизведения сейшевых колебаний [2-5], в которых распределение термодинамических величин считается заданным, и, таким образом, сейши не влияют на вертикальное перемешивание. Единственный известный автору подход для параметризации эффекта сейш на вертикальное перемешивание в водоёме, развиваемый в работах [6,7], основан на гипотезе, что энергия крупных сейшевых мод посредством нелинейного взаимодействия переходит на малые масштабы, на которых волны разрушаются на наклонном дне. Этот эффект параметризуется добавлением в уравнение баланса турбулентной кинетической энергии дополнительного слагаемого, форма которого конструируется из соображений размерности. В настоящей работе предлагается другой метод учёта сейш в одномерной модели водоёма, основанный на явном воспроизведении первой горизонтальной моды, несущей в озёрах наибольшую энергию. Этот метод реализован в модели озера LAKE.

Одномерная модель термогидродинамики и биогеохимии водоёма и нижележащего грунта LAKE [1,9,10] явно описывает процессы вертикального переноса тепла с учётом проникновения коротковолновой радиации в слоях воды, льда, снега и нижележащего грунта (донных отложений). Уравнения модели сформулированы относительно осреднённых по горизонтальному сечению водоёма величин, что приводит к явному учёту обмена импульсом, теплом и растворёнными газами между водной средой и наклонным дном. В толще воды используется к — е параметризация турбулентности, а в уравнениях движения учтён баротропный градиент давления[1].Вслое снега учитывается перенос жидкой фазы влаги, а в слое грунта - возможность ее замерзания. В модели описывается вертикальная диффузия растворенных газов (СО2,СЩ, О2), а также их пузырьковый перенос, окисление метана, фотосинтез и процессы потребления кислорода. Включена параметризация генерации метана в грунте под водоёмом [10], причём для случая термокарстовых озер предложена оригинальная формулировка для производства метана на нижней границе протаявшего грунта (талика). Модель проверялась на способность воспроизведения термического и ледового режимов большого числа водоёмов в контрастных климатических условиях, в том числе в рамках проекта LakeMIP (Lake Model Intercomparison Project [11-14]).

Статья построена следующим образом. В разделе 2 приводятся уравнения одномерной модели в общем виде, используемые в модели LAKE, формулируется проблема их замыкания. Затем в разделе 3 выписывается известная многослойная модель стратифицированной жидкости, выводится её вид для первой горизонтальной моды сейшевых колебаний. В разделе 4 производится замыкание уравнений одномерной модели с помощью уравнений для первой моды многослойной модели. В разделе 5 излагаются результаты тестов новой модели на известных аналитических решениях, демонстрируется влияние параметризации сейш и силы Кориолиса на скорость заглубления верхнего перемешанного слоя в термоклин. В заключении формулируются основные выводы работы.

2.    Система уравнений одномерной модели водоёма

Рассмотрим водоём произвольной формы. Введём операцию осреднения произвольной скалярной величины f по его горизонтальному сечению A(z): f = A^-1 (z) /д) f dA', где z - координата, направленная вдоль силы тяжести. Применяя эту операцию к уравнению притока тепла и уравнениям движения для горизонтальных компонент скорости в приближении несжимаемой жидкости, получаем [1]:

дТ -AT +     (a (Am + vt ) дТ \ - Adz           dz ; 1 dAS 1 dA _ (1) dt Adz + Adz [Sb 1 Fr’b(z)], du dt -Au ДX   +       + Vm)+ p; dx / A dz           dz / 1 dA      X A dz Fu'b(z^ + lV, (2) dv = dt -Av " / 1 dp\   1 d            dv - U dy) + AgzV(v + vm)ai) + 1 dA A J Fv,b(z) lu, A dz (3) где Т - температура, (u, v) = Uh горизонтальная скорость, Am, v - коэффициенты моле кулярной температуропроводности и вязкости соответственно, vt, vm - их турбулентные аналоги, p; - плотность воды, l - параметр Кориолиса, р - давление, S - кинематический поток коротковолновой радиации [м/с -К], A = A-1(z)

f (uh • n)dl - вклад переноса

^Г А (Р

величины f через границы водоём а притоками и стоком (n - внешняя нормаль к грани це горизонтального сечения водоёма Гщг)). Нижний индекс «6» указывает на значения потоков соответствующих величин на границе Гщг), т.е. на дне водоёма. Хорошим приближением в большинстве случаев является S = Sb- Частные случаи приведённой системы уравнений решаются во многих одномерных моделях [2,6,16-18]. Система (1) - (3) решается в модели LAKE 2.0, где средний горизонтальный градиент давления рассчитывается как баротропный градиент [1] (подробнее см. ниже).

В настоящей работе основной задачей является параметризация слагаемых с градиентом давления в (2) - (3) для общего, бароклинного, случая, т.е. когда водоём стратифицирован по плотности. Наиболее просто эта задача решается для водоёма в форме [-Lx/2, Lx/2"\ х [—Ly/2,Ly/2] x [0,H\, из чего, в частности, следует A(z) = const, что существенно упрощает систему (1) - (3). Именно эта форма предполагается в дальнейшем изложении.

3.    Многослойная модель стратифицированной жидкости3.1.    Исходные уравнения и сохранение энергии

В модели многослойной жидкости тело водоема состоит из N слоёв постоянной плотности p i, p i+i > p i (нумерация вдоль силы тяжести), толщина которых испытывает малые возмущения относительно средних значений, h i = H i + h i , (|hi/Hi| ^ 1, ^І=і H i = Н^. Для каждого слоя можно записать линеаризованные уравнения для импульса и массы (здесь и далее - без суммирования по повторяющимся индексам) [19]:

dui      1 dpi dt = pi dx + lVi, (4) dvi      1 dpi dt      pi dy    Пі- (5) d-h + H. (dr + dr) =0-dt       dx dy (6) N pi    9   > pmin(i,k) hk, ^    1,N. (7) к=1

Частным случаем этой системы при N = 1 являются известные линеаризованные уравнения мелкой ВОДВІ. Полная кинетическая энергия системы (4) - (7) определяется как

1 ^N        Г-_у L^x

+ и²) dxdy.

к = 9 Е H i p i

2 i=1      0000

Введём величину

_о^N      СЧ -Lx / N \ ²

А = ^>#4       Е^И dxdy, i=1                  kk=i/ где Api = pi и Api = pi — pi-i при г > 2. Используя уравнения (4) - (7), можно доказать, что

d(K + А) dt.

(Ю)

Величина А является обобщением на многослойный случай доступной потенциальной энергии двухслойной жидкости, введённой в [3], и получена в настоящей статье, насколько известно автору, впервые. Из (9) легко видеть, что состоянию покоя системы (4) - (7) (Ui , U i , h i = 0, г = 1,N) соответствует минимальное значение А = 0. Закон сохранения полной энергии должен быть адекватно отражён в параметризации сейш, а также соблюдён при построении численной схемы этой параметризации.

• 3.2.    Многослойная модель для первой горизонтальной моды

Рассмотрим трёхмерный водоём [—L_x/2, L_x/2] х [— L y /2 L y /2] х [0, Н ] без вращения, т.е. положим в системе (4) - (7) I = 0. Воспользуемся известным в лимнофизике фактом [2-5, 21,22], что в озёрах энергия мод с первым горизонтальным волновым числом преобладает в спектре внутренних колебаний, и разложим решение до первой гармоники Фурье:

лx            ^x\ . ^луХ

Ui = иш cos     J + un cos J sin J , лу\    1 . /лx       лу\

= U01 cos       + «1 1sin ^-) cos       , лx            лу            лх\ . /лу\ hi = h\o sin     J + Һ01 sin     J + h\i sin     J sin j .

Подставляя это решение в (4) - (7), вводя величины, осреднённые по левой и правой частям горизонтального сечения /^Х1 = 2/(L_xL y ) J⁰- /2 /^--^//₂ f^dx, /^x2 = = 2/(L_xL_y ) J^-2/² J—-^//₂/dydx, аналогично определяя / ^y 1 и /^y2, получаем

du- лд N E pmin^Ax¥k, k=1 (И) dt 2Lxpj dUj лд N E pmin(j^) Ay HP, k=1 (12) dt 2Ly pj dAxh‘   2лН,

=-1^,

^У» =2лН1 -, ,3 =TTN,(14)

dt Ly где Axh'j = h'j — hj - средний перепад давления вдоль оси x для первой моды, a Ayh'- - средний перепад давления по оси у. Заметим, что уравнения (11) и (13), с одной стороны,

и (12) и (14) - с другой, представляют собой независимые системы. Теперв учёт ускорения Кориолиса можно получить формальным добавлением в правые части (11) и (12) слагаемых +lt> j и — lu j соответственно, что делает систему (11) - (14) связанной.

Система (11) - (14) также обладает законом сохранения полной механической энергии А + К = const, где

1 ^N

^К = 2 Е ^H i P i ^L x L y (п² + г²) , ^Z г=1

N

А = - С ^ _Др, г=1

/ N       \ ²   / N      \ ²

Е Axhk  + Е A, Ч .

\ к=г       /      \k=i       /

4.    Параметризация сейш на основе многослойной модели

Примечательным свойством системы (11) - (14) является то, что она связывает средние по горизонтали компоненты скорости со средним градиентом давления, что позволяет их использовать для замыкания системы (1) - (3). Однако уравнения (1) - (3) являются дифференциальными по z, в то время как в системе (11) - (14) вертикальные профили гидродинамических величин являются кусочно-постоянными. В настоящей статье сопряжение двух систем не обосновывается математически строго, поэтому будет правильно называть результирующий метод учёта горизонтального градиента давления в одномерной модели параметризацией.

В непрерывном по вертикали профиле плотности воды, определяемом текущим профилем температуры в одномерной модели, выделим слои [zj, zj+Д, Hj = ^zj+1 ^{— z}j, ^j = ^1,N в каждом из которых плотность меняется по глубине незначительно, и введём величины pj = H^-1 J^^^j+1 p(z)dz. Введём для этих слоёв переменные A_xh'j , A,hj, для расчёта которых согласно формулам (13) - (14) будем использовать компоненты скорости из одномерной модели, осреднённые по вертикали в пределах соответствующего слоя: (uj^j ) = H^-1 JZ'¹' (U,u)dz. Далее, получаемый из A_xhj, А,hj, j = 1,N, средний горизонтальный градиент давления есть кусочно-постоянная функция глубины, с постоянным значением внутри каждого интервала [zj , zj+1). Дополненные этим градиентом давления уравнения движения одномерной модели (2) - (3) принимают вид (напоминаем, что A(z) = const):

du dt

-

d        du

— (v + v_m)---lv = dz        dz

-

^g 2L x P₃

дг dt

-

^{д (}v + v m )   ^{+ lu} = ^—

N

E Pmin(j,k) ^Ax^hk, ^{j : z} € ^[z j ^,Z j+1 ), k=1

N

5 у ^pmin(j,k)^A, ^h k , ^j • ^{z € [z} j , ^z j+1 ), k=1

^dA x ^h j    2ttHj

dt

L x

U, j = 1,N,

dA, hj _ 2-/у.

dt

L,

$, j = 1,N,

- Z''-

^(u j ^,r j ) = ^H j         ⁽u,v^)dz, ^j = 1, N.

J Zj

Полученная система решается методом расщепления в два этапа:

• 1)    Расчёт тенденции компонент скорости за счёт градиента давления вместе с шагом по времени уравнений (19) - (21) схемой Кранка-Николсон. Можно показать, что при этом выполняется сохранение величины А + К ((15) - (16)). Возникает система

линейных уравнений с плотной матрицей, которая решается прямым методом; при характерных значениях N ~ 2 ... 10 время решения этой системы почти не сказывается на общем времени расчёта моделью LAKE.

• 2)    Расчёт тенденции компонент скорости за счёт вязкости и ускорения Кориолиса. Здесь также используется схема Кранка-Николсон, по вертикали применяются центральные разности, система линейных уравнений решается методом прогонки.

5.    Идеализированные численные эксперименты5.1.    Свободные гравитационные колебания

Отметим, что использованный здесь подход сопряжения системы (11) - (14) с системой уравнений одномерной модели использовался ещё У. Свенссоном [23], но при N = 1, т.е. воспроизводились только баротропные гравитационные колебания.

Поскольку помимо вертикальной структуры течения в изложенной выше модели явно воспроизводится также горизонтальная структура по заданной форме (1-я мода), модель правильно классифицировать как 11/2-мерную.

Задача данного численного эксперимента заключается в проверке пространственной структуры и частоты свободных гравитационных колебаний, возникающих в построенной 11/2-мерной модели, при сравнении с известными дисперсионными соотношениями.

Для эксперимента были приняты следующие условия:

• •    глубина водоёма 5 м, длина водоёма 2900 м;

• •    температура в начальный момент времени линейно убывает с глубиной, с градиентом

3 °C

• •    в качестве уравнения состояния исполв':дуется линеаризованное отіюсптелвію 15 °C уравнение из [24]; градиенту температуры 3 °С/м соответствует частота Брента-Вяйсяля N = No = 6.6 • 10^-2 с^-1:

• •    начальный профиль компоненты скорости по оси ж принимается линейным, с максимальным значением 10 - 2 м/с на поверхности и 0 на дне, вторая компонента скорости задаётся нулём;

• •    напряжение ветра на поверхности т = 0, на дне трение даётся квадратичным законом;

• •    сила Кориолиса не учитывается.

Вследствие неучета силы Кориолиса г равнялась 0 в течение всего эксперимента.

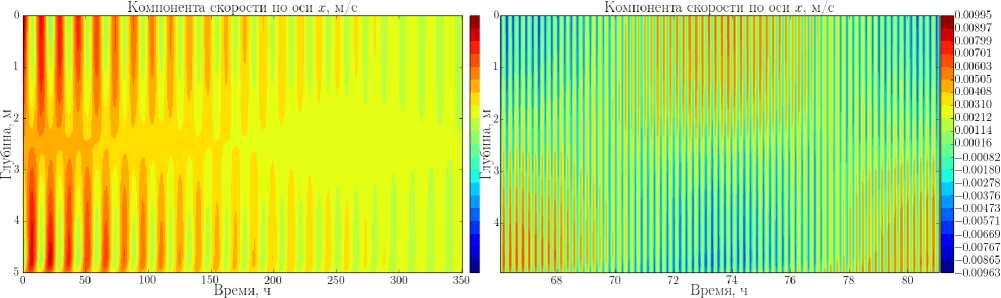
На рис. 1а представлено пространственно-временное распределение скорости течения. Как видно, ампилитуда колебаний затухает со временем в силу внутренней вязкости и трения о дно. Вертикальное распределение скорости и соответствует первой вертикальной моде, таким образом, в модели явно воспроизведена мода H1V1. Период колебаний можно визуально оценить из рис. 1а как ~ 15.5 ч. Однако в решении присутствуют и более высокочастотные колебания - см. «развёртку» одного периода моды H1V1 на рис. 16. Вертикальная структура этих колебаний соответствует моде H1V0 (баротропная мода), а период можно оценить как ~13 мин.

Для теоретической оценки периода баротропных мод традиционно используются линейные одномерные уравнения мелкой воды, из которых следует классическая, многократно подтверждённая наблюдениями формула Мериана [25]:

Т =

2U

Для оценки частот бароклинных мод можно привлечь линеаризованные уравнения Буссинеска для двумерной области с твёрдой крышкой, которые при подстановке волнового решения сводятся к задаче Штурма-Лиувилля для амплитуды вертикальной скорости W1 [19]:

d²W dz²

(⁵ — ¹) ^=0-

W |г=0 = WUh = 0, где к - горизонтальное волновое число, для первой моды равное tt/Lx, ш - частота. Формула Мериана дает Т = 13.8 мин, а решенная методом стрельбы задача (23) - набор вертикальных мод и связанных с ними периодов, среди которых моде H1V1 соответствует Т = 14.7 ч, что близко к полученным выше значениям из модели LAKE.

а)

б)

Рис. 1. Пространственно-временное распределение компоненты скорости по оси х в численном эксперименте со свободными гравитационными колебаниями (а). В колебаниях видно преобладание моды H1V1. На рисунке б) показано то же, по за. один период моды H1V1. Здесь колебания соответствуют моде H1V0 (баротропная сейша)

5.2.    Эффект параметризации сейш на перемешивание в сдвиговом стратифицированном потоке

В настоящем разделе рассматривается эффект разработанной выше параметризации сейш на перемешивание в стратифицированном водоеме, возникающее при постоянном потоке импульса, на. верхней границе. Такая постановка, задачи позволяет воспроизвести упрощённый аналог летнего заглубления перемешанного слоя в термоклин в озёрах умеренных широт. При этом эффект сейш на. глубину перемешанного слоя будет сопоставлен с влиянием вращения (силы Кориолиса).

Для решения поставленной задачи с моделью LAKE проведено четыре группы численных экспериментов. Основой всех экспериментов является постановка. Като-Филлипса2 со следующими параметрами:

• •    глубина водоема 5 м;

• •    температура в начальный момент времени линейно убывает с глубиной, с градиентом 3 ^оСм:

• •    в качество уравнения состояния испо.ть::іуетея линеаризованное относительно 15 °C уравнение из [24]; градиенту температуры 3 °С/м соответствует частота Брента-Вяйсяля N = No = 6.6 * 10^-2 с^-1:

• •    в начальный момент времени п = 0, г = 0;

• •    горизонтальный градиент давления не учитывается;

• •    напряжение ветра на поверхности т = 10^-2 Н/м², на дне трение даётся квадратичным законом;

• •    сила Кориолиса не учитывается.

Группы экспериментов отличаются в постановке от условий Като-Филлипса:

• •    Эксперимент K-P+bts (Kato-Phillips + barotropic seiches). Средний горизонтальный градиент давления рассчитывается по параметризации баротропних сейш (т.е. N = 1 в (17) -(21)).

• •    Эксперименты K-P+bcs (Kato-Phillips + baroclinic seiches). Средний горизонтальный градиент давления рассчитывается по параметризации бароклинних сейш, описанной в п.4³.

• •    Эксперимент K-P+kor. Постановка эксперимента Като-Филлипса дополняется учётом горизонтальных ускорений Кориолиса, с параметром Кориолиса, соответствующим широте N ° с.ш.

• •    Эксперименты K-P+kor+bcs. Постановка Като-Филлипса с добавлением ускорения Кориолиса и параметризации бароклинных сейш.

В тех группах экспериментов, где используется параметризация сейш, параметрами модели становятся горизонтальные размеры водоема. Когда в модели принимаются во внимание и вращение, и стратификация (серия K-P+kor+bcs), естественно рассмотреть три случая: L_x = L_y = L ^ L r, L _x = L_y = L = L r и L _x = L_y = L » L r. Учитывая, что при выбранной стратификации и широте L r ~ 2770 м, в расчётах принимались значения L = 300 м, L r = 2770 м, 300 км. Кроме того, в природе часто встречаются вытянутые водоемы с преимущественно продольным направлением ветра (например, озёра, окружённые лесом или высоким рельефом), длина которых может превышать внутренний радиус деформации Россби, а ширина - быть значительно меньше Lr. Поэтому в серию K-P+kor+bcs были добавлены эксперименты с L_x = 300 км, Ly = 300 м.

Рассмотрим рис. 2. Быстрее всего водоём перемешивается в эксперименте Като-Филлипса. Более медленно заглубление перемешанного слоя происходит при включении баротропного градиента давления. Наиболее медленно перемешивание происходит в экспериментах с включённым вращением или бароклинными сейшами.

Близость результатов экспериментов с вращением и бароклинными сейшами неслучайна. Как в случае вращающегося бесконечного слоя жидкости, так и для замкнутого бассейна с бароклинными сейшами достигаются квазистационарные режимы течения, в которых силы Кориолиса и горизонтального градиента давления соответственно компенсируют в балансе импульса перемешанного слоя приток импульса из атмосферы. Это, при прочих равных условиях, уменьшает скорость в перемешанном слое, останавливает рост сдвиговой генерации ТКЭ и «затормаживает» заглубление перемешанного слоя. Квазистационарное течение при вращении описывается профилем, близким к спирали Экмана, а при наличии бароклинного градиента давления в замкнутом водоёме это течение можно получить в стационарном варианте уравнений (11) - (14) при N > 2, если в них добавить трение на поверхности.

В двух же экспериментах, в которых толщина перемешанного слоя росла быстрее всего, квазистационарное течение не достигается. Так, в постановке Като-Филлипса в балансе импульса перемешанного слоя присутствует только приток импульса из атмосферы при слабом молекулярном трении на нижней границе слоя; таким образом, средняя скорость в перемешанном слое непрерывно растёт, растёт сдвиговая генерация ТКЭ и заглубление верхнего слоя. При добавлении в систему баротропного градиента давления квазистационарное течение также невозможно. Это можно показать, используя уравнения (11) - (14) для, например, двухслойной жидкости, если добавить в них трение на поверхности и заменить градиент давления в правой части баротропным градиентом. Тогда при условии стационарности эти уравнения примут вид

0 = £ -   ДЛ,

Н   2L_X ^{ж 1} ’

0 = - Дх Ц, 2L_X^{х 1} ’

^1 = ^2 = о, т.е. становятся несовместными.

Глубина перемешанного Глубина перемешанного Глубина перемешанного Глубина перемешанного модели, К-Р модели, К-Р+сог модели, K-P+bts модели, K-P+bcs

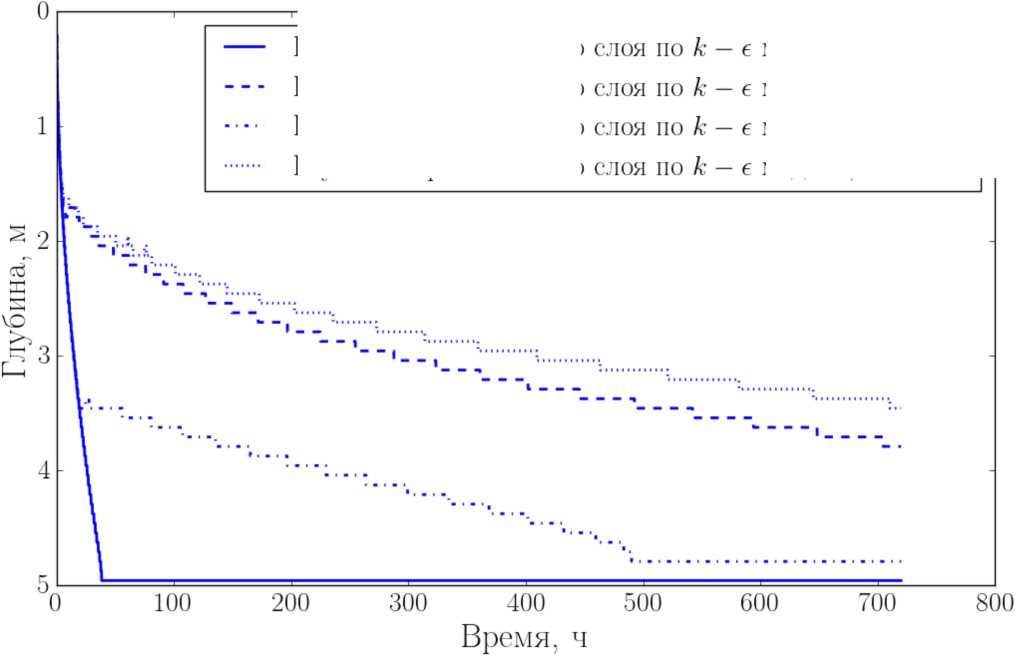
Рис. 2. Эволюция глубины перемешанного слоя в эксперименте Като-Филлипса (К-Ф), в эксперименте К-Ф, дополненном учётом силы Кориолиса, в эксперименте К-Ф с включенной параметризацией баротропных сейш и в эксперименте К-Ф с включенной параметризацией бароклинных сейш (результаты моделирования), L _x = L^ = L r

Обратимся теперь к рис. 3. Из него видно, что скорость заглубления перемешанного слоя слабо чувствительна к включению вращения при L <С L r и п ри L = Lr. Однако при L ^ L r учёт силы Кориолиса значительно ограничивает скорость загрубления верхнего слоя. Объясняется это тем, что горизонтальный градиент давления при L ^ L r растёт во времени при заданном потоке импульса из атмосферы очень медленно, не успевая обеспечить стационарное течение, так что вращение оказывается значительно более эффективным механизмом подавления вовлечения перемешанного слоя в термоклин.

И, наконец, на рис. 4 видно, что в случае, когда ширина водоёма сильно меньше Тд, а длина - сильно больше Тд, включение силы Кориолиса слабо влияет на заглубление перемешанного слоя. Это согласуется с известными теоретическими представлениями, что именно ширина озера является пространственным масштабом, определяющим роль силы Кориолиса [29].

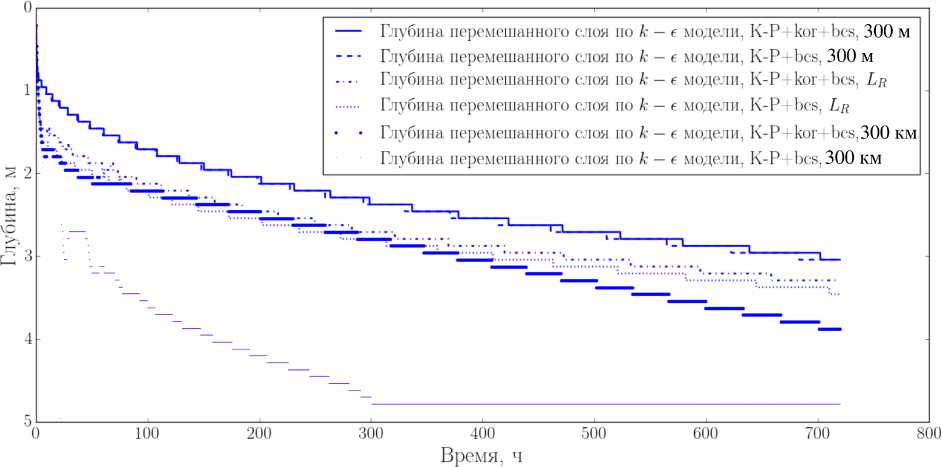
Рис. 3. Эволюция глубины перемешанного слоя в эксперименте Като-Филлипса, дополненном учетом силы Кориолиса и параметризацией бароклинных сейш (результаты моделирования), при горизонтальных размерах озера: 300 х 300 м, L_r х L_r и 300 х 300 км (Lr ^ 2770 м)

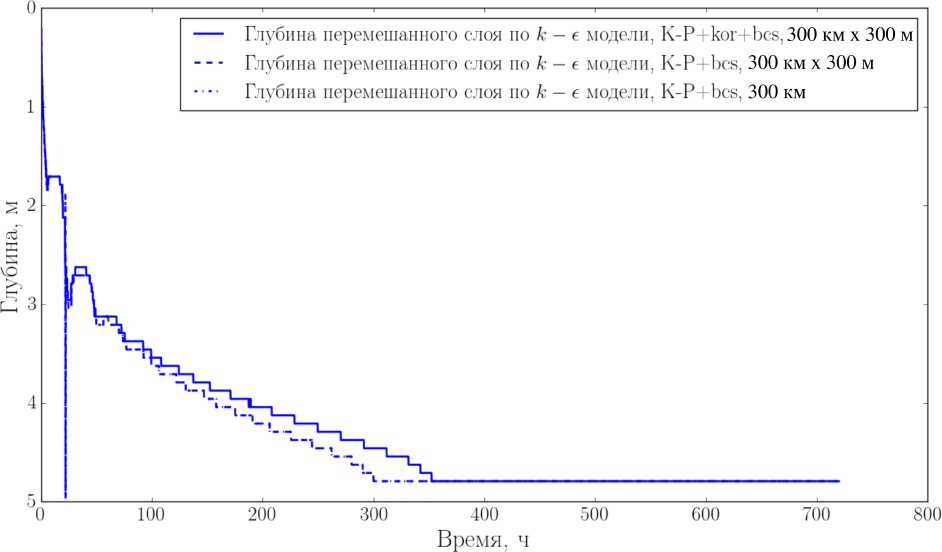
Рис. 4. Эволюция глубины перемешанного слоя в эксперименте Като-Филлипса, дополненном учетом силы Кориолиса и параметризацией бароклинных сейш (результаты моделирования), при горизонтальных размерах озера: 300 км х 300 м и 300 х 300 км

6.    Заключение

Итак, в настоящей работе предложен метод замыкания (параметризации) горизонтально осреднённых одномерных уравнений гидродинамики замкнутого водоёма в части расчёта ускорения за счёт горизонтального градиента давления. Замыкание достигается привлечением модели многослойной жидкости в предположении, что горизонтальная структура поля скорости и давления задана только первой горизонтальной модой. Попутно впервые получено выражение для доступной потенциальной энергии многослойной модели. В результате замыкания в одномерной модели появляются сейшевые колебания с первым горизонтальным волновым числом, а множество «разрешённых» моделью вертикальных волновых чисел определяется текущей стратификацией озера. Данная параметризация включена в модель водоёма LAKE. Дополнительное время на расчёт параметризации оказалось очень малым по сравнением с общим временем интегрирования модели.

С дополненной таким образом моделью LAKE произведены тестовые расчёты. В численных экспериментах, воспроизводящих свободные колебания в водоёме, частоты баротропных и бароклинных колебаний в модели хорошо согласуются с теоретическими оценками на основе линейных моделей. В расчётах заглубления сдвигового перемешанного слоя в нижележащий термоклин при постоянном потоке импульса из атмосферы (аналог летнего заглубления эпилимниона в озёрах) показано следующее:

• •    сила Кориолиса в неограниченном горизонтальном слое жидкости и горизонтальный градиент давления (~ сейши) в ограниченном водоёме подавляют скорость заглубления сдвигового перемешанного слоя в устойчиво стратифицированный нижележащий слой по сравнению со случаем неограниченного горизонтального слоя без вращения и горизонтального градиента давления;

• •    при горизонтальном размере водоёма L порядка внутреннего радиуса деформации Россби L r (для средних широт и не очень глубоких озёр L r ~ 2-3 км) влияние сейш и вращения на глубину перемешанного слоя сравнимо, при L ^ L r вращение значительно сильнее подавляет заглубление эпилимниона, а при L ^ L r значительно больше ограничивают его развитие сейши.

Из этих выводов можно сделать следующее заключение о применимости классических одномерных моделей водоёма (без учёта горизонтального градиента давления, но с силой Кориолиса) к вычислению летней стратификации озёр. При L &  L r эти модели применимы, но при L ^ L r они должны завышать глубину летнего перемешанного слоя. Последнее утверждение подтверждается результатами моделирования небольших озёр, когда приходится заново калибровать параметры моделей или привлекать трудно проверяемые гипотезы о наличии дополнительных физических механизмов, подавляющих вертикальное перемешивание [11].

Ещё одним важным результатом включения параметризации сейш в одномерную модель стало появление придонного сейшевого течения и соответствующего ему турбулентного пограничного слоя (в данной статье не обсуждается), в то время как в классических одномерных моделях горизонтальная скорость отлична от нуля только в верхнем перемешанном слое. Наличие придонного пограничного слоя хорошо известно из данных наблюдений [30], и оно важно для вертикального переноса растворённых веществ, в т.ч. парниковых газов, из донных отложений.

На основе дополненной модели LAKE в настоящее время ведутся расчёты характеристик сейш в озёрах, для которых имеются детальные измерения внутренних колебаний.

Работа выполнена в Московском государственном университете имени М.В. Ломоносова при поддержке гранта РНФ 17-17-01210 «Исследование процессов взаимодействия атмосферного пограничного слоя умеренных и высоких широт с деятельным слоем суши и водоёмами: разработка параметризаций для моделей Земной системы».