Параметры цифрового канала, построенного на базе непрерывного многолучевого релеевского канала

Описание канала связи, как и любого физического объекта, фактически является его идеализацией, которая отражает его наиболее существенные (с точки зрения решаемой задачи) свойства и, таким образом, определяет лишь некоторую модель реального объекта.

Модель канала должна быть построена таким образом, чтобы содержать всю информацию о реальном канале, необходимую и достаточную для разработки обслуживаемой им системы связи и в первую очередь – для выбора оптимальной структуры и алгоритмов работы передающего и приёмного устройств. Кроме того, математическая модель канала используется для последующего построения на её основе аппаратной или программной модели – имитатора канала, необходимого для испытаний или сертификации аппаратуры связи [1].

Внутри дискретного канала всегда содержится непрерывный канал. Преобразование непрерывного канала в дискретный осуществляет модем. Поэтому в принципе можно вывести математическую модель дискретного канала из моделей непрерывного канала при заданном модеме. Такой подход обычно приводит к сложным моделям, особенно для многолучевых каналов, каковыми являются, в частности все каналы мобильной связи.

Однако существуют сравнительно простые модели дискретного канала, при построении которых свойства непрерывного канала и модема не учитывались. Одна из таких моделей – марковская модель дискретного канала с памятью [2]. При проектировании системы связи всегда имеется возможность варьировать в довольно широких пределах модель дискретного канала при заданной модели непрерывного канала путём изменения модема.

Переход от релеевской модели замираний аналогового канала к марковской модели дискретного канала

Будем считать, что в заданном аналоговом канале действуют гладкие медленные релеевские замирания и аддитивный белый гауссовский шум.

Обозначая

Y =

U вых

U вх

– коэффициент передачи канала, введём 2 меры

2E помехозащищённости: ho =------ отношение энергии сигнала на входе

N 0вых

2E канала к спектральной плотности шума на его выходе - и h =-----

–

N0вых обычное SNR. Тогда h2 = h2 у2. Задача состоит в том, чтобы найти зависимость между двумя событиями: ошибка в приёме некоторого символа (ош1) и ошибка в соседнем символе (например, в следующем – ош2). Поскольку замирания медленные, считаем Yi = Y2 = Y и, следовательно, Рош1 (Y1) = Рош2 (Y2 ) = Рош (y) • Шум в соседних тактовых интервалах независимый, следовательно, и ошибки (при фиксированном значении Y) также независимы. Значит,

^Р ош1, ош2 ( y ) = ^Р ош1 ( y ) ■ ^Р ош2 ( y ) = ^Р ош ( y ) •

После усреднения по у :

^Р ош1, ош2 ^Р ош1 ^Р ош2   ^Р ош ^.

Теперь Р ш _ош2 = Р ( ош1, ош2 ) является совместной вероятностью двух подряд ошибок безотносительно к величине у , а Р _{ш 1} = Р ( ош1 ) и

Рош2 = Р ( ош2)

– соответственно являются отдельными вероятностями

ошибок. Чтобы найти условную вероятность ошибки во втором символе при условии ошибки при приёме первого символа, воспользуемся теоремой умножения вероятностей:

Р(ош1, ош2) = Р(ош1)- Р(ош2|ош1). Отсюда следует:

Р(ош2|ош1) = Р(ош1, ош2)/Р(ош1).

Найдём эти вероятности для двоичной модуляции ортогональными сигналами и некогерентной демодуляции. При этом

Рош (y) = 1e-h22 = 1e-h02 Y’/2

.

Так как замирания аппроксимируются релеевским законом

Y    -Y 2/ 2 o ²

w ⁽ Y ) = — e

Q

, то для получения средней вероятности ошибки

^Р ош = ^Р ( ^ош ) = ^Р ( ^ош1 ) используем формулу полной вероятности:

Р(ош) = £°Рош (y) ■ w(y) • dY = £°1 e h0Y2/2■

w (y)^ dY =

= ” 1e-h y72,2L e

J° 2         Q2

-Y 2/ 2 a ² ■

d y .

„Y2 Г 1    ,.2)

и интегрируем:

Используем подстановку и = — —у + h₀

P ( ош ) =----- = , где Y 2 = 2 а ² и h 2 Y2 = h 2 - среднее отношение

2 + ho2 y 2

сигнал/шум на входе демодулятора.

Теперь находим P ( ош1, ош2 )

как усреднённое по Y значение

Рош1 (y)- Рош2 (y)= Pi. (y) :

го                                   го 1

P ( ^{ош1, ош2} ) = J_o ^р ош ( y ) ^- w ( y ) ^- d Y = J₀ -e

h ^{0 Y} - w ( y ) - d Y =

=   ^ro le - h o² y ² -^ e -Y²/2_a 2 - d y .

0 4       Q2

„Y2 Г 1

Теперь используем подстановку и = — —у + 2 h

и интегрируем:

P (ош1, ош2) =

4 + 4 h2 Y2

4 + 4 h h-

Для нахождения условной вероятности P(ош2|ош1) разделим второе выражение на первое:

P ( ош2| ош1 ) =

1     /   1   _ 2 + h2

4 + 4 h 2/2 + h 2  4 + 4 h 2

Сравним P(ош2|ош1) с P(ош2):

2 + h2      1   ________

--=T > 0

4 + 4 h 2  2 + h 2  (4 + 4 h

Видно, что условная вероятность Р ( ош2|ош1 )

всегда больше, чем

безусловная вероятность Р ( ош2 ) =--- =л. Лишь при h ² = 0

2 + h 2

(вырожденный случай «обрыва канала») Р ( ош2|ош1 ) = Р ( ош2 ) =

. По

мере увеличения h2 ^ да Р(ош2) ^0, а Р(ош2|ош1)

^ —. Это явно

указывает на группирование ошибок.

Аналогично найдём Р ( прав2|ош1 ) . Для этого сначала определим

^Р ош1, прав2 ^{( y )} = ^Р ош1 ^{( y} ) ' ^Р прав2 ^{( y )} = ^Р ош ^{( y )( 1   Р}ош ^{( y} ) ) •

p       ЛЛ =1 e-h- Y2 2

^Р ош1, прав2 ^{( Y )}   2e        I

по Y найдём Р (ош1, прав2) •

1 - 1e - h o Y72

. Теперь путём усреднения

Р(ош1, прав2)= ”1 e-h»Y2/2•( 1 -1 e-h-2YY2 1Л-e-YV2"2.

v ,            0 2          I 2         Ja2

2 + 3 h 2

. И, наконец,

(2 + h 2 II4 + 4 h2)

2 + 3 h

1     2 + 3h2

.

2 + h 2  4 + 4 h 2

Найдём сумму обеих условных вероятностей:

P ( ош2| ош1 ) + P ( прав2| ош1 )

2 + h ²   2 + 3 h ²  ,

---= +---= = 1.

4 + 4 h ²  4 + 4 h ²

Аналогично найдём P ( прав2|прав1 ) и P ( ош2|прав1 ) :

P ( прав 1, прав2 ) = J^ ( 1 - — e

h 0 Y2/ 2

.Le-fh^- a ² e

. Далее:

P (прав) = 1 - P (ош) =

1 + h o ² Y ²

1 + h h

P ( прав2|прав1 ) =

1 + h h

■ h ²)/ 2 + hh

Сравним P ( прав2|прав1 ) с P ( прав2 ) = P ( прав ) :

P ( прав2|прав1 ) — P ( прав2 ) =

1 + h h

x---^= h2 )   2 + h h1

4 + 10 h ² + 8 ( h ² ) 2 + 2 h ² + 5 ( h ² ) 2

I — 4 — 8 h ² — 4 h ²^ — 4 h ² — 8 h^\

(h2)’

4 ( 1 + h ² )

> 0 .

Видно, что условная вероятность P ( прав2|прав1 ) всегда больше, чем

1 ^{+ h 2} безусловная вероятность P ( прав2 ) =--- =. Это указывает на

2 + h h группирование и правильных решений. Далее находим

P ( прав1, ош:

«Г

2 ) =[  1 - -

- 0 (   2

e

—

e

J 2

—h2 Y2/2 Y    y2/2< a2 e

2 + 3 h ²

. И, наконец,

( 2 + h ² )( 4 + 4 h ² )

P ( ош2|прав1 ) =

2 + 3hh

2 + 3h h

.

4 + 4 h ² 11 1 + h ² )

Для проверки вычисляем

2 + 5 h ² + 4

(p )2

2)+(

2 + 3 h ²

4 + 4 h ² )( 1 + h ² )

4 + 8 h ² + 4 ( h ² ) 2 ( 4 + 4 h ² )( 1 + h ² )    4 (

4 ( 1 + h ² ) 2

1 + h ² )( 1 + h ² )

= 1 . Проверка сошлась. Итак,

P ( прав2|прав1 )

P ( ош2|прав1 )

P ( ош2|ош1 )

P ( прав2|ош1 )

2+5 h2 +4 (h2) _2±Л 4 (1 + h2 )2      4 + 4 hh

2 + 3 h2       2 + 3h2

4 (1 + h2 )2      4 + 4 h 2

Таким образом, вычислены все 4 элемента матрицы переходных вероятностей марковской цепи ошибок и правильных решений, описывающей рассматриваемый дискретный канал.

Приведённый ниже рисунок показывает зависимость вероятностей:

P ( ош2|прав1 ) (P1) – вероятность принять символ ошибочно, если предыдущий был прият правильно;

P ( ош2|ош1 ) (P2) – вероятность принять символ ошибочно, если предыдущий был принят ошибочно;

• (p) – средняя вероятность ошибочного приёма символа.

  

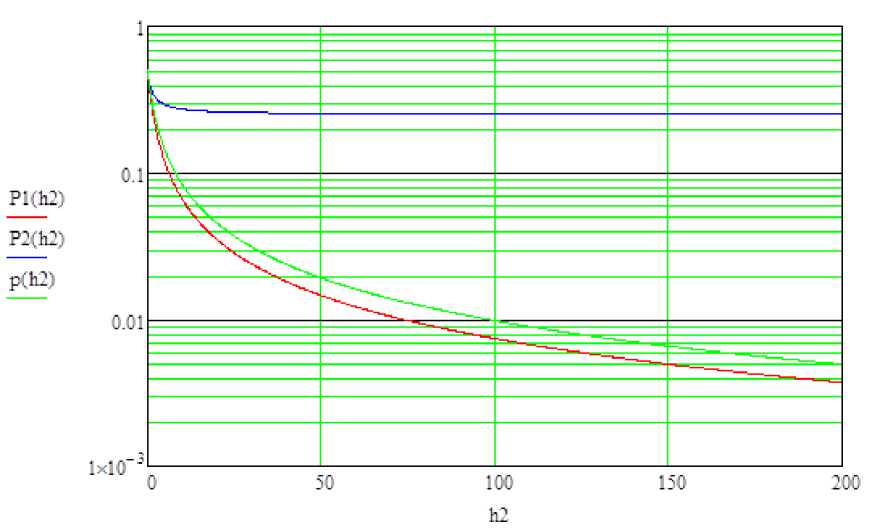
  Рис. 1. Графики зависимостей вероятностей ошибок.