Параметры и характеристики термомеханического компрессора при работе с криогенным рабочим телом

котемпературный потенциал рабочего тела (его физическое низкопотенциальное тепло), а тепло внешней среды для нагрева в горячей полости, то есть компримирования. При этом по предварительной оценке степень повышения давления составляет величину около 1,2. Это позволит обеспечить прокачку рабочего тела через газификатор в саму ёмкость.

Расчёт термокомпрессора для такой установки предполагает значительные осложнения в методике. Так, например, возможен влажный режим компрессора, при котором в холодную полость поступает не испарившаяся часть рабочего тела. Кроме того, температура и давление в ёмкости постоянно растут, соответственно меняются термодинамические параметры рабочего тела, поступающего в термокомпрессор.

Предлагаемая методика расчёта термокомпрессора учитывает эти особенности и реальность рабочего тела. Известные методики [3, 4] предполагают использование идеального рабочего тела, что некорректно на уровнях криогенных температур и высоких давлений.

Исходные данные и обозначения:

Т _г – температура газа в горячей полости;

Т _х – температура газа в холодной полости;

Т _рег – температура газа в регенераторе;

р _Н – давление на входе в ТМК;

р _В – давление на выходе из ТМК;

V _Т –объём,описываемый поршнем-регенератором;

рабочее тело – азот (N2);

V _г и V _х – текущие объёмы горячей и холодной полостей;

m - текущая масса рабочего тела в ТМК;

R – удельная газовая постоянная;

с _г и ^ _х – плотности рабочего тела в горячей и холодной полостях;

c _v и c _p – изохорная и изобарная теплоёмкости рабочего тела;

U – внутренняя энергия рабочего тела.

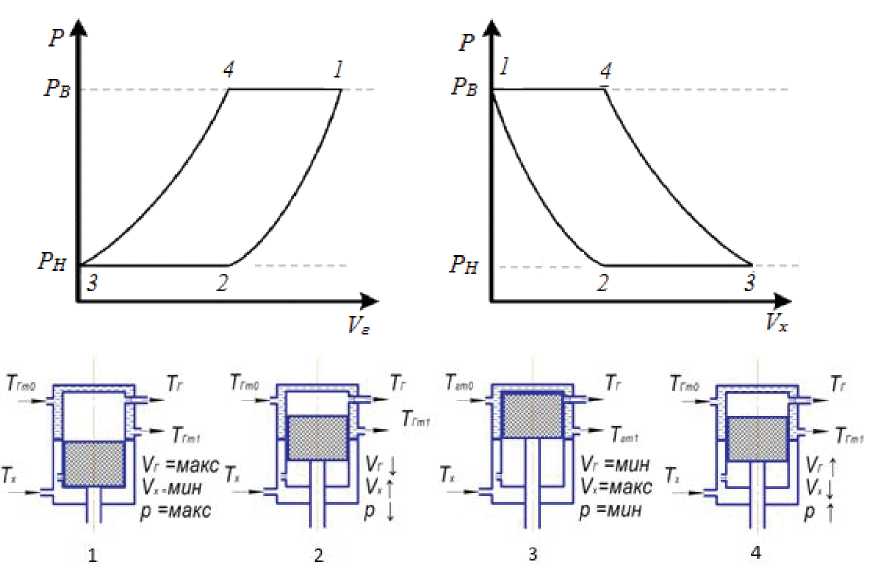
Рис. 1. Рабочий цикл термокомпрессора:

1-2 – перемещение газа из горячей области в холодную (Рv); 2-3 – впуск газа (Рмин);

3-4 – перемещение газа из холодной полости в горячую (Р^); 4-1 – нагнетание газа (Рмакс)

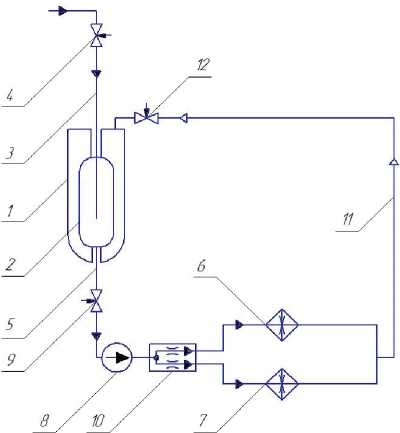
Рис. 2. Схема газификатора на основе баллона с криогенной заправкой:

1 – внешний сосуд; 2 – внутренний сосуд; 3 – магистраль заправки; 5 – магистраль опорожнения; 6,7 – теплообменник-испаритель; 8 – термокомпрессор; 9 - клапан; 10 – распределитель; 11 – магистраль подачи газа высокого давления; 12 – вентиль

Допущения:

• 1)    Отсутствие перепада давления на клапанах;

• 2)    Изотермичность процессов в горячей и холодной полостей;

• 3)    Объём регенератора равен нулю и степень регенерации равна 100%;

• 4)    Мертвые объёмы равны нулю;

• 5)    Газ нагнетается при температуре, равной температуре холодной полости;

• 6)    Давление в полостях термокомпрессора одинаково.

При этом для всех точек рабочего цикла следующие параметры остаются неизменными:

Тг=const, Тх=const, Vх+Vг=Vт=const.

Значения остальных термодинамических параметров определяются следующим образом:

Точка 1: Р1=Рв; Vг1=Vт, Vх1=0;

Точка 2:

ρГ1- ρГ2

2 н , ' х2 т г2 ; V r 2 V T       _

ρГ2- ρХ2

Точка 3: Р3=Pн; Vг3=0; Vх3=Vт;

Точка 4:

.

Р =Р V =V -V / V_x. = V_T ^Р Г ^{4 Р} Х ³

4 в, г4 т х4     X 4       Т

ρ _{Г 4} - ρ _{Х 4}

.

Плотности рабочего тела определяются по давлению впуска и выпуска и температуре горячей и холодной полостей.

Определим перенос работы из горячей полости в холодную:

W 1-2 = J , pdV r .

W r 2 - 3 = Р н ( V r 3 - V r 2 ) .

W r 3 - 4 = J 3⁴ pdV r .

W r 4 - 1 = Р н ( V r 1 - V r 4 ) .

Интегрирование производится методом прямоугольников, заключающемся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке.

Тепло, подводимое к горячей полости в течение процесса, равно сумме изменения внутренней энергии вещества, содержащегося в полости, изменение энтальпии за счёт привнесённого в полость вещества и работы, подведенной к рабочему телу в течение этого цикла.

А / Г ,2 + Q r ,2 = A U Г ,2 + W r ,2 .

Для изотермических процессов, каковыми являются истечение газа из любой из полостей:

^A m r J2 С РГ Т Г + Q r ₁2 — ^Am r ,2 ^C vr ^T r + W r 12 .

^Q r 12 ^{— ( С} VГ ^{— С} РГ ) ' Т Г "  ⁽ m r 2 ^— m r 1 ) ^{+ W} Г 12 ■

6 г 12 ^{— ( C} V ^— c P ^{) Т}Г ^{( Р} г 2 ^V Г 2 ^{— Р} г 2 ^V Г 1 ^{) + W} Г 12 ■

Аналогично для других процессов

Q r 23 — U г з — U г 2 + ( m r з — m r 2 ) h r + —

— (cvr — cpr )Tr ( 0 — pr 2 ' Vr 2 ) + Wr 23 ■ подведенной теплоты в зависимости от степеней повышения давления и отношений температур приведены на рис. 3 и 4 соответственно. Пунктирными линиями представлены значения соответствующих показателей, рассчитанных при условии, что рабочее тело в термокомпрессоре – идеальный газ [3].

Исходя из полученных результатов, можно сделать вывод, что при малых степенях повышения давления характеристики термокомпрессора, рассчитанного при условии работы на реальном газе, незначительно отличаются от характеристики термокомпрессора, работающего на идеальном газе. Заметные отличия наблюдаются при больших уровнях давления и рк, что обусловлено отличием свойств идеального и реального газов.

Таким образом, параметры процессов и характеристики термокомпрессора с реальным рабочим телом в области криогенных температур несущественно отличаются от таковых для идеального газа и вполне приемлемы для практического применения в описанных выше устройствах.

Q r 34    ⁽ c V   c P ^)Tr ^{( p} r 4 ^V r 4   ^p r3 ^V r 3 ^{) + W} r 34

Q r 41   ^UГ 1   ^UГ 4 ⁺⁽ m r 1   m r 4 ) h r ^{+ W}r 41

^{— (} c V ^— c P ) T r ^{( p} r 1 ^Vr 1 ^{— p} r 4 ^Vr 4 ^{) + P}B ^{( V}r 1 ^{— V}r 4 ).

Расчёты показали, что тепло, подводимое к горячей полости в процессах 2-3 и 4-1, пренебрежимо мало (в случае, например, с идеальным газом равно нулю), поэтому считаем, что QГ23 и QГ41 равны нулю.

Тепло, отводимое от холодной полости:

Q x 12 — ( C v ~ C p )T_X ( P x 2 ( V — V r 2 ) ) — W r 12 .

^QХ 34

^{— (} c v

- Cp ) T x

[ P h ( V — V r 4 )

I RT x

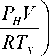
w

Г 34^.

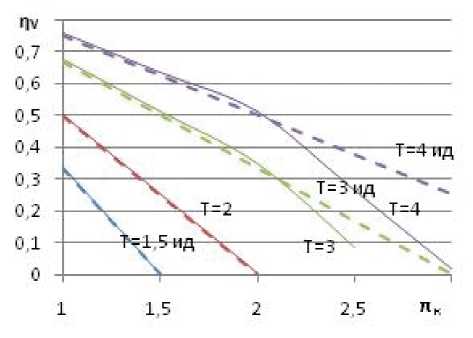
Рис. 3. Зависимость объёмного кпд от степеней повышения давления и отношений температур

Аналогично QГ23 и QГ41 тепло, отводимое от холодной полости в течение процессов 2-3 и 4-1, принимаем равным нулю.

Для анализа эффективности термокомпрессора были определены некоторые показатели эффективности: объёмный КПД и безразмерная подведенная теплота.

Объёмный КПД определяется по выражению nv —

m ₃ — m ₂ m ₃

а безразмерная подведенная теплота по выражению

Qnd

Q r 12 + Q Г 34

RT_x ( m ₃ — m ₂ )

Значения объёмных КПД и безразмерной

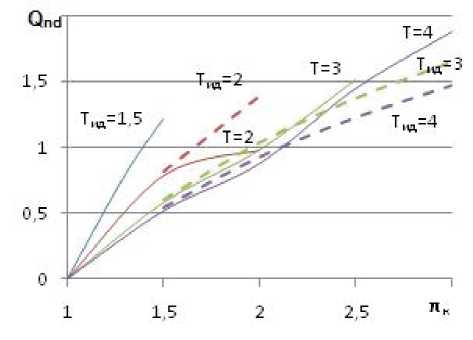
Рис. 4. Зависимость безразмерной подведенной теплоты от степеней повышения давления

и отношений температур