Параметры оптимизации для системы связи на базе беспилотных летательных аппаратов
Автор: Ржевский Сергей Иванович, Чертова Ольга Георгиевна
Рубрика: Управление сложными системами
Статья в выпуске: 4, 2018 года.
Бесплатный доступ
В статье представлен процесс выбора параметров, с помощью которых осуществляется оптимизация системы связи на базе беспилотных летательных аппаратов (БЛА) в условиях динамически изменяющейся окружающей среде. Данная система обеспечивает связью абонентов с необходимым качеством.
Программный модуль, программа, сеть связи, беспилотный летательный аппарат, модуляция
Короткий адрес: https://sciup.org/148309012
IDR: 148309012 | УДК: 004.42, | DOI: 10.25586/RNU.V9187.18.11.P.102
Текст научной статьи Параметры оптимизации для системы связи на базе беспилотных летательных аппаратов
Для организации связи на базе малоразмерных БЛА следует определить исходные данные, которыми будем пользоваться при решении задачи оптимизации: пропуск ная способность c, отношение сигнал/шум (ОСШ) —, скорость передачи данных N0
R и вероятность ошибки Pв, где c и R должны быть максимальными, а Pв минимальным [1]. При этом остальные параметры сети – количество БЛА, высота барражирования БЛА, расстояние между ними, способ модуляции, частота и мн. др. – являются переменными. Для нахождения переменных параметров сети найдем их зависимость от исходных данных, которые представлены в табл. 1.
Таблица 1
Исходные данные для решения задачи многокритериальной оптимизации
|
Пропускная способность канала c , бит/с |
E ОСШ / N 0 |
Скорость передачи данных R , бит/с |
|
S ^ С = w log 2 1 1 + N 1 , (1) w – ширина полосы пропускания; N – средняя мощность шума; S – мощность принятого сигнала |
E SW = (2) N 0 NR ,() R – скорость передачи данных в битах в секунду |
log M R = , (3) T – длительность n -битового символа; k – число битов в символе; M = 2 n – размер алфавита (кратность модуляции) |
ВЕСТНИК РОСНОУ. Серия «Сложные системы…»
Для определения вероятности ошибки требуется знать способ модуляции сигнала. Для решения задачи организации связи на БЛА используется стандарт WiMAX, в котором применяется масштабируемый OFDM-доступ с возможностью автоматической подстройки манипуляции от QPSK до QAM под условия динамически изменяемой окружающей среды [2].
Вероятность появления ошибочного бита QPSK
Вероятность появления ошибочного бита при когерентном детектировании сигнала QPSK :
( ^
p = Q E— в ' \2N0 )
где Q ( x ) – гауссов интеграл ошибок.
Q ( x )
72П
да Г
J exp x \
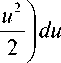
где u и du являются заменами следующих выражений:
z - a?, dz
u = -, du =
°0
где a 0 - дисперсия шума; z - случайная гауссова переменная со средним значением a 1 или a 2, в зависимости от того, передавался двоичный ноль или двоичная единица, определяется по формуле:
z = a , + n о , (7)
где n 0 – шумовой компонент (случайная гауссова переменная с нулевым средним).
Таким образом, формула (5) примет следующий вид:
Q ( x )
72л
да
J exp
x
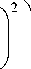
d
' a, + n о
I ao
™ 2
Q ( x ) « / |exp - 2( a n 0 0 a 2) d
2n J. a 2
' a , + n о
I a o
Подставив x , получим вероятность появления ошибочного бита при когерентном детектировании сигнала QPSK (формула (4)):
^ ^
Q J-E^
W2 N о
V2n
<
J exp
I
2 N 0
2( a i + n о — a 2 )
^
d
)
ai + n 0
^ 0
Значения данной функции определены в табл. 2.
Таблица 2
|
Q ( x ) |
||||||||||
|
0 x |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
0,0 |
0,500 0 |
0,496 0 |
0,492 0 |
0,488 0 |
0,484 0 |
0,480 1 |
0,476 1 |
0,472 1 |
0,468 1 |
0,464 1 |
|
0,1 |
0,460 2 |
0,456 2 |
0,452 2 |
0,448 3 |
0,444 3 |
0,440 4 |
0,436 4 |
0,432 5 |
0,428 6 |
0,424 7 |
|
0,2 |
0,420 7 |
0,416 8 |
0,412 9 |
0,409 0 |
0,405 2 |
0,401 3 |
0,397 4 |
0,393 6 |
0,389 7 |
0,385 9 |
|
0,3 |
0,382 1 |
0,378 3 |
0,374 5 |
0,370 7 |
0,366 9 |
0,363 2 |
0,359 4 |
0,355 7 |
0,352 0 |
0,348 3 |
|
0,4 |
0,344 6 |
0,340 9 |
0,337 2 |
0,333 6 |
0,330 0 |
0,326 4 |
0,322 8 |
0,319 2 |
0,315 6 |
0,312 1 |
|
0,5 |
0,308 5 |
0,305 0 |
0,301 5 |
0,298 1 |
0,294 6 |
0,291 2 |
0,287 7 |
0,284 3 |
0,281 0 |
0,277 6 |
|
0,6 |
0,274 3 |
0,270 9 |
0,267 6 |
0,264 3 |
0,261 1 |
0,257 8 |
0,254 6 |
0,251 4 |
0,248 3 |
0,245 1 |
|
0,7 |
0,242 0 |
0,238 9 |
0,235 8 |
0,232 7 |
0,229 6 |
0,226 6 |
0,223 6 |
0,220 6 |
0,216 8 |
0,214 8 |
|
0,8 |
0,216 9 |
0,209 0 |
0,206 1 |
0,203 3 |
0,200 5 |
0,197 7 |
0,194 9 |
0,192 2 |
0,189 4 |
0,186 7 |
|
0,9 |
0,184 1 |
0,181 4 |
0,178 8 |
0,176 2 |
0,173 6 |
0,171 1 |
0,168 5 |
0,166 0 |
0,163 5 |
0,161 1 |
|
1,0 |
0,158 7 |
0,156 2 |
0,153 9 |
0,151 5 |
0,149 2 |
0,146 9 |
0,144 6 |
0,142 3 |
0,140 4 |
0,137 9 |
|
1,1 |
0,135 7 |
0,133 5 |
0,131 4 |
0,129 2 |
0,127 1 |
0,125 1 |
0,123 0 |
0,121 0 |
0,119 0 |
0,117 0 |
|
1,2 |
0,115 1 |
0,113 1 |
0,111 2 |
0,109 3 |
0,107 5 |
0,105 6 |
0,103 8 |
0,102 0 |
0,100 3 |
0,098 5 |
|
1,3 |
0,096 8 |
0,095 1 |
0,093 4 |
0,091 8 |
0,090 1 |
0,885 |
0,086 9 |
0,085 3 |
0,083 8 |
0,082 3 |
|
1,4 |
0,080 8 |
0,079 3 |
0,077 8 |
0,076 4 |
0,074 9 |
0,073 5 |
0,072 1 |
0,070 8 |
0,069 4 |
0,068 1 |
|
1,5 |
0,066 8 |
0,065 5 |
0,064 3 |
0,063 0 |
0,061 8 |
0,060 6 |
0,059 4 |
0,058 2 |
0,057 1 |
0,059 9 |
|
1,6 |
0,054 8 |
0,053 7 |
0,052 6 |
0,051 6 |
0,050 5 |
0,049 5 |
0,048 5 |
0,047 5 |
0,046 5 |
0,045 5 |
|
1,7 |
0,044 6 |
0,043 6 |
0,042 7 |
0,041 8 |
0,040 9 |
0,040 1 |
0,039 2 |
0,038 4 |
0,037 5 |
0,036 7 |
|
1,8 |
0,035 9 |
0,035 1 |
0,034 4 |
0,033 6 |
0,032 9 |
0,032 2 |
0,031 4 |
0,030 7 |
0,030 1 |
0,029 4 |
|
1,9 |
0,028 7 |
0,028 1 |
0,027 4 |
0,026 8 |
0,026 2 |
0,025 6 |
0,025 0 |
0,024 4 |
0,023 9 |
0,023 3 |
|
2,0 |
0,022 8 |
0,022 2 |
0,021 7 |
0,021 2 |
0,020 7 |
0,020 2 |
0,019 7 |
0,019 2 |
0,018 8 |
0,018 3 |
|
2,1 |
0,017 9 |
0,017 4 |
0,017 0 |
0,016 6 |
0,016 2 |
0,015 8 |
0,154 0 |
0,015 0 |
0,014 6 |
0,014 3 |
|
2,2 |
0,013 9 |
0,013 6 |
0,013 2 |
0,012 9 |
0,012 5 |
0,012 2 |
0,011 9 |
0,011 6 |
0,011 3 |
0,011 0 |
|
2,3 |
0,010 7 |
0,010 4 |
0,010 2 |
0,009 9 |
0,009 6 |
0,009 4 |
0,009 1 |
0,008 9 |
0,008 7 |
0,008 4 |
|
2,4 |
0,008 2 |
0,008 0 |
0,007 8 |
0,007 5 |
0,007 3 |
0,007 1 |
0,006 9 |
0,006 5 |
0,006 6 |
0,006 4 |
|
2,5 |
0,006 2 |
0,006 0 |
0,005 9 |
0,005 7 |
0,005 5 |
0,005 4 |
0,005 2 |
0,005 1 |
0,004 9 |
0,004 8 |
|
2,6 |
0,004 7 |
0,004 5 |
0,004 4 |
0,004 3 |
0,004 1 |
0,004 0 |
0,003 9 |
0,003 8 |
0,003 7 |
0,003 6 |
|
2,7 |
0,003 5 |
0,003 4 |
0,003 3 |
0,003 2 |
0,003 1 |
0,003 0 |
0,002 9 |
0,002 8 |
0,002 7 |
0,002 6 |
|
2,8 |
0,002 6 |
0,002 5 |
0,002 4 |
0,002 3 |
0,002 3 |
0,002 2 |
0,002 1 |
0,002 1 |
0,002 0 |
0,001 9 |
|
2,9 |
0,001 9 |
0,001 8 |
0,001 8 |
0,001 7 |
0,001 6 |
0,001 6 |
0,005 1 |
0,001 5 |
0,001 4 |
0,001 4 |
|
3,0 |
0,001 3 |
0,001 3 |
0,001 3 |
0,001 2 |
0,001 2 |
0,001 1 |
0,001 1 |
0,001 1 |
0,001 0 |
0,001 0 |
|
3,1 |
0,001 0 |
0,000 9 |
0,000 9 |
0,000 8 |
0,000 8 |
0,000 8 |
0,000 8 |
0,000 8 |
0,000 7 |
0,000 7 |
|
3,2 |
0,000 7 |
0,000 7 |
0,000 6 |
0,000 6 |
0,000 6 |
0,000 6 |
0,000 6 |
0,000 5 |
0,000 5 |
0,000 5 |
|
3.3 |
0,000 5 |
0,000 5 |
0,000 5 |
0,000 4 |
0,000 4 |
0,000 4 |
0,000 4 |
0,000 4 |
0,000 4 |
0,000 3 |
|
3,4 |
0,000 3 |
0,000 3 |
0,000 3 |
0,000 3 |
0,000 3 |
0,000 3 |
0,000 3 |
0,000 3 |
0,000 3 |
0,000 2 |
Гауссов интеграл ошибок
Q ( x ) из формулы (10) не всегда можно вычислить в аналитическом виде, поэтому пользуются аппроксимацией, справедливой для x >3 [1].
Q (x) ~ — exp -V l.
xV2n^
Для дальнейшего упрощения представления предлагается не расписывать гауссов интеграл ошибки.
ВЕСТНИК РОСНОУ. Серия «Сложные системы…»
Вероятность появления ошибочного бита при когерентном детектировании сигнала в дифференциальной модуляции QPSK:
PB = 2 Q
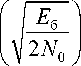
(
I - Q
A
I I E 6
W 2 N о ))
Вероятность появления ошибочного бита при модуляции QAM:
P _ 2(1 — L"1) Q ( 1 3log 2 L 2 E 6 " B log 2 L ^H L 2 — 1 N о I
,
где L = МЙ - количество уровней амплитуды в одном измерении; M- размер набора символов.
В формулах (1–4), (10), (12) и (13) прослеживается зависимость параметров друг от друга. С помощью математических преобразований составим зависимость всех параметров друг от друга, опираясь на формулы вероятности ошибки. Формулу (1) можно представить в следующем виде:
, N + S c = w log2—— . (14)
NS Продолжим преобразование, чтобы выражение получилось относительно , где
.
S – мощность принятого сигнала, N – средняя мощность шума.
log2
N + S c
N + S .
при условии, что ——— > 0 , получим
2 w
Nw ,
c
2 w
-
N + S
N,
1 = 2 N
.
Подставим (17) в формулу (2):
Nt = (2
c
w
—
W 1) W .
R
Подставим в (18) скорость передачи данных из формулы (3):
E^- = (2 ^ — 1) ^W-
.
N 0 log2 M
T
Таким образом, получено выражение для подстановки в гауссов интеграл ошибок. Рассмотрим на примере, подставим значение из (19) в формулу (4):
PB = Q ^2 (2
c
w —
1) -TW_ log2 M ^
.
Аналогичным способом расписываются выражения для других вероятностей появления ошибочного бита. Представим только конечные варианты.
Вероятность появления ошибочного бита при когерентном детектировании сигнала в дифференциальной модуляции QPSK:
C
PB = 2 Q l-(2 w k^ 2
—
TW
1) —— log2 M 7
1 c
1 — Q л -(2 w
—
TW
1) TW log2 M
\
.
Вероятность появления ошибочного бита при модуляции QAM:
р . 2(1—LD Q 1, 2 в log 2 L П
3lOg 2 L (2 W — » TW L — 1 ( 4og2 m
.
Распишем значения пропускной способности, количество уровней амплитуды в одном измерении, длительность n-битового символа и среднюю мощность шума для упрощения расчетов.
T = 1 , V
где V – скорость передачи информации (бит/с). S
Для цифровых каналов связи в отношении мощность шума часто замещают спектральной плотностью мощности шума: N
N = kL s L 0 ,
где k = 1,38 - 10 23 Дж/к или ВТ/КГц = -228,6 дБВт/КГц;
т ( 4 пd Y
Ls = II - потери в тракте или потери в свободном пространстве, если при-V X у нимающая антенна не является изотропной, то Ls = (4пd)2;
X = — - длина волны несущей, где c « 3 -108 - скорость света; f - рабочая частота;
d – расстояние между приемо-передающим модулем (ППМ) и абонентом;
L0 – включает в себя большой набор различных источников ослабления и ухуд- шения.
Таким образом, N = k(4пd)2L0, а вероятность принятия ошибочного бита примет следующий вид:
P e 2(1 — Ж
B log 2 V M
2 3log 2 M
M — 1
w
1+ S k (4л d )2 Lo
— 1
W
k
k
V log2 M "
Опираясь на формулу (25), в табл. 3 сведем параметры, от которых будет зависеть дальнейшая оптимизация.
Таблица 3
Параметры оптимизации
|
Параметр |
Характеристика |
Размер ность |
Диапазон принимаемых значений |
|
d |
расстояние между ППМ и абонентом |
м |
2– 3000 |
|
L 0 |
все ослабления и ухудшения |
дБ |
0–∞ |
|
S |
мощность принятого сигнала |
Вт |
до 159 |
|
W |
ширина полосы пропускания |
МГц |
1,25; 5; 10; 20 |
|
M |
размер алфавита (кратность модуляции) |
– |
4; 16; 32; 64 |
|
V |
скорость передачи информации |
бит/с |
до 75 |
ВЕСТНИК РОСНОУ. Серия «Сложные системы…»
При построении системы связи разработчики стремятся минимизировать все ослабления и ухудшения сигнала, т.е. L 0 → min, а скорость – увеличить, т.е. V → max. Однако невозможно улучшить один параметр, не ухудшив при этом другой. К примеру, увеличение скорости V → max приводит к уменьшению кратности модуляции M → min , что влечет за собой уменьшение расстояния между ППМ и абонентом и уменьшение ширины полосы пропускания. При постоянном значении Pв = 10–6 [3].
Таким образом, необходим переход к решению задачи многокритериальной оптимизации.
В общем виде такую задачу можно представить следующим образом. Пусть X обозначает множество допустимых решений в некоторой задаче, X ϶ x v – допустимое решение.
Предположим, что каждое решение x е X оценивается по m критериям, в предложенном случае m = 6 ( d , L 0, S , W , M , V ).
Таким образом, получены параметры, с помощью которых можно регулировать настраиваемую сеть связи.
Список литературы Параметры оптимизации для системы связи на базе беспилотных летательных аппаратов
- Чертова О.Г. Принципы построения и управления опорной ad-hoc сети связи на базе малоразмерных беспилотных летательных аппаратов / Сборник докладов Пятой межвузовой студенческой конференции, Москва, 25 марта 2016 г. / под общ. ред. канд. техн. наук Н.Э. Ненартовича. М.: НПО «Алмаз», 2016. С. 68-72.
- Скляр Б. Цифровая связь. Теоретические основы и практическое применение / под ред. А.В. Назаренко. М.: Вильямс, 2004. 1099 с.
- Чертова О.Г. Формализация задачи оптимизации управления топологией опорной сети связи на базе малоразмерных беспилотных летательных аппаратов / Сб. научн. ст. по материалам IV Всероссийской науч. практ. конф. «Академические чтения» (23-24 ноября 2016 г.). Воронеж: ВУНЦ ВВС «ВВА», 2017. С. 207-209.


