Параметры взаимодействия гусеничной машины с препятствием

Наиболее сложным из преодолеваемых препятствий является вертикальная стенка. С подъёмом передней части гусеничной машины на вертикальную стенку увеличивается угол наклона машины и уменьшаются при этом необходимые для этого подъёма тяговые усилия гусеницы.

Определим соотношение скоростей движения оси ведущей звёздочки по горизонтальной поверхности и оси натяжного колеса по вертикальной стенке. Будем считать, что такое движение гусеничной машины является плоскопараллельным.

Из теоретической механики известно, что в плоскопараллельном движении проекции скоростей двух точек фигуры на прямую, соединяющую эти точки, равны между собой. Следовательно, проекции скоростей натяжного катка и ведущей звёздочки на гусеницу должны быть равны.

Из рис. 1 видно, что

V cos в = VHK COs(900 -e) = VHK sin P или cos В        _

VHK = V3e---x = V3ectg в нк     зв             зв sm p где  Vзв – горизонтальная скорость движения ведущей звездочки гусеницы;

V нк – горизонтальная скорость движения натяжного катка гусеницы;

P - угол наклона гусеничной машины.

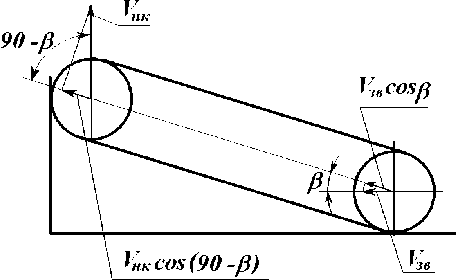
Рис. 1. Схема движения гусеничной машины на вертикальную стенку

Уравнение (2) показывает, что в начале подъёма натяжного катка на вертикальную стенку скорость движения оси ведущей звёздочки значительно превышает скорость оси натяжного колеса. Скорость же гусеницы одинакова как у ведущей звёздочки, так и у натяжного колеса. Это означает, что, поскольку гусеница у натяжного колеса не может проскальзывать по вертикальной стенке и должна развивать тяговое усилие, гусеница относительно горизонтальной поверхности должна интенсивно пробуксовывать, полностью реализуя свои сцепные возможности. По мере увеличения угла наклона гусеничной машины при подъёме на вертикальную стенку интенсивность буксования гусеницы по горизонтальной поверхности будет уменьшаться. При угле наклона гусеничной машины, равном 450, ctgP = 1. Это означает, что гусеница движется по вертикальной и горизонтальной поверхностям либо без буксования, либо с пробуксовкой одинаковой интенсивности. Если угол наклона гусеничной машины превысит 450, то с пробуксовкой будет перемещаться гусеница по вертикальной поверхности. По горизонтальной же поверхности гусеница будет перемещаться без буксования. Последнее объясняется тем, что с увеличением угла наклона гусеничной машины увеличивается весовая нагрузка на ведущую звёздочку, а необходимая суммарная сила тяги по горизонтальной и вертикальной поверхностям уменьшается.

Определим предельную высоту порогового препятствия, которое может преодолеть гусеничная машина. Примем допущение, что гусеница не прогибается внутрь контура гусеницы. Схема преодоления порогового препятствия показана на рис. 2.

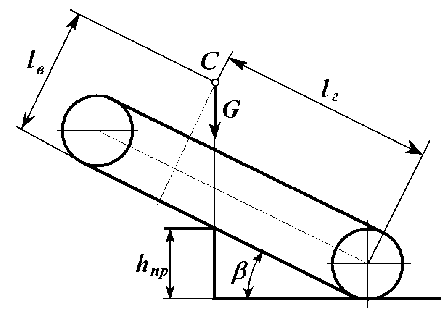
Рис. 2. Схема преодоления гусеничной машиной порогового препятствия: G - вес машины;

l ; l - соответственно вертикальная и горизонтальная (относительно ветвей гусеницы) координаты центра тяжести гусеничной машины; С - центр тяжести гусеничной машины;

h - высота порогового препятствия; β - угол наклона гусеничной ветви к горизонтальной поверхности

Из данных рис. 2 следует, что преодоление такого препятствия возможно тогда, когда линия действия силы тяжести машины пройдёт через полку порога.

С целью упрощения решения поставленной задачи будем считать, что радиус ведущей звёздочки (рассматриваем гусеничную машину с задним расположением ведущей звёздочки) равен нулю. Тогда схему преодоления машиной порогового препятствия можно представить следующим образом (рис. 3).

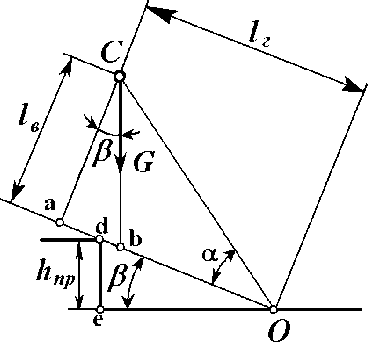
Рис. 3. Упрощённая схема преодоления гусеничной машиной порогового препятствия при условии, что радиус ведущей звёздочки равен нулю

Из данных, приведённых на рис. 1–3, становится очевидно, что гусеничная машина не преодолеет пороговое препятствие, если ab+dOaO = 1г.(3)

Положение машины, при котором линия действия силы тяжести проходит через край порогового препятствия, определяется равенством ab+dO = aO = lr.

Машина преодолевает пороговое препятствие, если ab + dO aO = lr.(5)

Определим значения величин, входящих в вышеприведённые выражения. Треугольник аСb подобен треугольнику dOe , поскольку эти треугольники прямоугольные и имеют углы с взаимно перпендикулярными сторонами (углы в ). Из этих треугольников получим:

ab ab tgP = — = — , ab = letgfi;

aCl de   hпр sin в = — = —^, dO = —— .

dO dOsin

Определим значение суммы этих отрезков, при которой линия действия силы веса гусеничной машины будет проходить через край порога.

ab + dO = Ltgp + h"  = I.

вг sin в

Отсюда найдём h„p = sinP(l г - 1рдв).

Разделив правую и левую части уравнения (9) на l , получим:

h„P = sin в( 1 - l в %в).

В этом уравнении      ^hпр      ^lв Графическое представление уравнения показано на рис. 4.

пр i ’ в Г гг

После наезда на пороговое препятствие угол в наклона машины при её дальнейшем движении будет увеличиваться. Соответственно будет увеличиваться и расстояние h от точки гусеницы, через которую проходит линия действия силы веса. Если это расстояние увеличиваться не будет, пороговое препятствие для гусеничной машины не будет преодолимым. Предельный угол наклона гусеничной машины ограничивается наступлением опрокидывания машины. Этот угол определяется прохождением линии действия силы веса машины через ось ведущей звёздочки. При этом впред

= 90⁰ - а = 90⁰ - arctgl-.

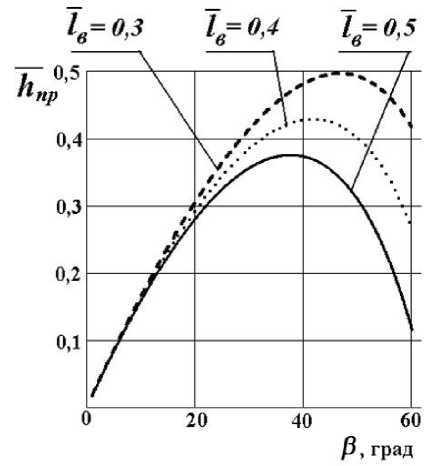
Рис. 4. Зависимость относительной высоты порогового препятствия от угла продольного наклона гусеничной машины по уравнению (10)

Для определения предельной допустимой высоты порогового препятствия (экстремума функции по уравнению (10)) продифференцируем уравнение (10) и полученную производную приравняем к нулю.

dh = cos в( 1 -lвtgP) -1 Bsin e( 1 + tg2p).

dp cosв( 1-letge) -1в sinP( 1 + tg2 e) = 0.

Преобразуем уравнение (13).

cos в - 21 в sin Д -1 Bsin ^tg2 в = 0.(14)

1- - ,

— - 2 1 в - 1 &² в = 0 .

tg в + 2 tgв-y = 0 . l_в

Полученное кубическое уравнение имеет следующее решение.

tg в =

1  81   181

+     +     +3     -     +

2l в     27   4lв2      2l в     274

Из уравнения (17) определяется и предельный угол наклона гусеничной машины при преодолении порогового препятствия.

в = arctg

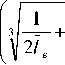
81  1  81

+     + 3      -     +

27  4 l ²     2 l     27  4 l ²

вв   в

Подставив значения tgв и предельного угла наклона гусеничной машины в уравнение (10), найдём предельную величину преодолеваемого порогового препятствия, меньшие значения кото- рой гусеничная машина может преодолеть, а большие значения высоты порогового препятствия для неё непреодолимы.

hпр

^{X 1} - l e к

= sin arctg к

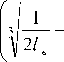
81   1

+      + 3

27   4l2     2l вв

--+

27  4 l ²

в

1  81   181

+     +    + 3     —+

2lв 27   4lв2     2lв 274

A

J)

X

Уравнение (19) позволяет определить предельную высоту порогового препятствия, преодолеваемого одновременно двумя гусеницами, в зависимости от конструктивных параметров двухгусеничной машины. Кроме этого, взаимодействие гусениц с нескальным пороговым препятствием, которое имеют сминаемые кромки, позволяет гусеничной машине уменьшить угол наклона к горизонтальной поверхности и тем самым увеличить высоту преодолеваемого порога.

Следует отметить, что сочленённая гусеничная машина, включающая в себя две соединённые сцепным устройством гусеничные тележки, способна преодолевать пороговые препятствия, превышающие определённые выше значения [3, 4, 5]. Это объясняется наличием в сцепном устройстве механизмов, позволяющих изменять угол между продольными осями передней и задней тележек. Указанное обстоятельство обеспечивает возможность изменять угол между продольной осью передней тележки и горизонтальной поверхностью и приподнимать тем самым натяжное колесо передней тележки над горизонтальной поверхностью.

Заключение . Разработаны расчетные схемы преодоления гусеничным трактором порогового препятствия. Создана математическая модель взаимодействия гусеничной машины с пороговым препятствием, которая позволяет при известных конструктивных параметров машины определить предельно возможную высоту преодолеваемого порога. Исследование процесса преодоления порогового препятствия показало, что высота преодолеваемого порога зависит от положения центра тяжести гусеничного трактора.