Партийная принадлежность президентов США, 1852-2016: анализ и прогнозирование

что связано с циклами либерализма и консерватизма в политическом процессе США. Авторегрессионная модель Х. Норпота [Norpoth, 2016], в которой учитывается доля голосов избирателей, поданных за кандидата-демократа на протяжении двух предыдущих выборов (электоральные циклы 4 и 8 лет) за период 1828-2012 гг., корректно предсказала победу Д.Трампа в 2016 г.

Д. Гэнс [Gans, 1985] с помощью простых статистик анализировал число голосов избирателей, поданных за кандидатов в Президенты США за период 1856 — 1980 гг. и сделал вывод, что последовательность партийной принадлежности Президентов США носит случайный характер. Поскольку данный вывод важен для возможности корректного прогнозирования, то автор решил проверить вывод Д.Гэнса [Gans, 1985] на более длинной последовательности с помощью более продвинутых статистических тестов, сформулировав следующую гипотезу.

Гипотеза. В последовательности партийной принадлежности Президентов США за период 1852-2012 гг. проявляются свойства случайности.

Поскольку проверка последовательностей на случайность, анализ и прогноз последовательностей, являются стандартными и хорошо разработанными задачами криптографии, для решения которых доказано множество теорем, разработано множество методов и получено множество полезных результатов, то в данном исследовании использовался криптографический подход.

Методика

Для проверки выдвинутой гипотезы была сформирована бинарная последовательность партийной принадлежности Президентов США за период 1852-2012 гг. [Historical presidential elections], где цифрой 1 обозначен республиканец, а 0 — демократ. Полученная бинарная последовательность представлена в таблице 1.

Таблица 1

Последовательность партийной принадлежности Президентов США за период 1852-2012 гг.

Год	Партия	Год	Партия	Год	Партия	Год	Партия
1852	0	1896	1	1940	0	1984	1
1856	0	1900	1	1944	0	1988	1
I860	1	1904	1	1948	0	1992	0
1864	1	1908	1	1952	1	1996	0
1868	1	1912	0	1956	1	2000	1
1872	1	1916	0	1960	0	2004	1
1876	1	1920	1	1964	0	2008	0
1880	1	1924	1	1968	1	2012	0
1884	0	1928	1	1972	1
1888	1	1932	0	1976	0
1892	0	1936	0	1980	1

Примечания. Цифрой 1 обозначен республиканец, 0 - демократ

Для проверки выдвинутой гипотезы был использован пакет стандартных статистических тестов NIST STS (NIST Statistical Test Suite) [Statistical Test Suite] Ф.Тейлора [Taylor, 2015]. Пакет NIST STS включает в себя 15 статистических тестов, которые предназначены для проверки гипотезы о случайности бинарных последовательностей. В данных тестах используются статистические свойства, присущие только случайным последовательностям. С данными тестами заинтересованный читатель может ознакомиться в официальном руководстве NIST STS [Statistical Test Suite]. Проверка бинарной последовательности на случайность в NIST STS осуществляется следующим образом. Если вычисленное значение p больше либо равно 0,01, то делается вывод о случайной последовательности по данному тесту. Eсли вычисленное значение p меньше либо равно 0,01, то делается вывод о том, что тестируемая последовательность по данному тесту неслучайна. Для общего вывода о случайности тестируемой последовательности требуется прохождение всех тестов. Скажем сразу, что последовательность партийной принадлежности Президентов США за период 1852-2012 гг. (табл.1), включает в себя только 41 наблюдение, что меньше рекомендуемого для некоторых тестов. Например, для частотного побитового теста [Statistical Test Suite], рекомендованное минимальное количество членов тестируемой последовательности n больше или равно 100, где n — количество членов последовательности, а для теста на произвольные отклонения [Statistical Test Suite] рекомендованное минимальное количество членов тестируемой последовательности n больше либо равно 1000000. Поэтому некоторые тесты применить не представилось возможным, поскольку их использование требует большей длины последовательности. В силу данного ограничения, полученные в проведенном исследовании результаты следует считать предварительными.

В проведенном исследовании были использованы следующие основные классы математических методов для анализа и прогнозирования последовательностей. Эконометрические авторегрессионные методы анализа и прогнозирования временных рядов из пакета Gretl [Gretl], вейвлет-анализ, реализованный в пакете Wavelet Toolbox MATLAB [MATLAB], «нейронные» сети, реализованные в пакете NeuroSolutions [NeuroSolutions], метод SVD (Singular Value Decomposition), реализованный в пакете CaterpillarSSA [CaterpillarSSA] и компьютерная система Data Mining «Ксения», для автоматического прогнозирования дискретных последовательностей, разработанная А.Е.Игнатовым и автором в 1994 г. в научно-исследовательском комитете «Системная социология» Российского общества социологов (РОС).

Использование множества алгоритмов и пакетов для анализа и прогнозирования бинарных последовательностей следовало из практики криптографии, а также из современной методологии и методики анализа информации Data Mining and Knowledge Discovery (см.: [Толстова, 2015]).

При прогнозировании использовался «Тест на следующий бит» [Yao, 1982], согласно которому для случайной последовательности не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей 0,5. «Тест на следующий бит» осуществлялся для результатов выборов Президента США в 2012 и 2016 гг. Для этой цели сначала построение моделей и обучение «нейронных» сетей проводились за период 1852 — 2008 гг. и прогноз осуществлялся на 2012 г., когда победил демократ Б.Обама. Затем, построение моделей и обучение «нейронных» сетей проводились за период 1852 — 2012 гг. и прогноз осуществлялся на 2016 г., когда победил республиканец Д.Трамп. За более ранние моменты времени, «тест на следующий бит» не проводился, в силу ограниченности длины последовательности и предположения, что на результаты прогноза могли повлиять различные закономерности в выделенных подпоследовательностях.

Использование «теста на следующий бит» преследовало две цели. Первая цель — тестирование бинарной последовательности (табл.1) на случайность. Вторая цель — выявление методов прогнозирования, которые корректно предсказали результаты выборов Президента США в 2012 и 2016 гг. В этой связи напомним, что тестирование построенных моделей на известном значении, которое не использовалось при построении модели или обучении «нейронной» сети (Cross Validation) — стандартная методическая процедура тестирования моделей прогнозирования, в том числе, моделей прогнозирования [Pollyvote] партийной принадлежности Президентов США.

Анализ

В таблице 2 представлены результаты тестирования бинарной последовательности партийной принадлежности Президентов США за период 1852-2012 гг. (табл.1) по тем статистическим тестам из пакета NIST STS [Statistical Test Suite], которые можно было применить из-за ограниченной длины последовательности. Всего было использовано 9 тестов из 15 возможных.

Таблица 2

Результаты тестирования последовательности партийной принадлежности Президентов США за период 1852-2012 гг.

Тест	Значение р	Интерпр етация результата теста
Частотный побитовый тест	0.43448	Случайность
Частотный блочный тест	0.62339	Случайность
Тест на последовательность одинаковых битов	0.31103	Случайность
Спектральный тест (дискретное Фурье преобразование)	0.49603	Случайность
Тест на совпадение неперекрывающихся шаблонов (длина шаблона 4 бита)	0001 - 0.99950 ООП - 0.09543 0111 - 0.02296 1000 - 0.99955 1100 - 0.75995 1110 - 0.75995	Случайность
Тест на периодичность	0.40601 0.49297	Случайность
Тест приблизительной энтропии	0.99393	Случайность
Тест кумулятивных сумм	0.42269	Случайность
Тест линейной сложности*	0.54378	Случайность

Примечания. *Значение для теста линейной сложности было вычислено в пакете STS-1.6 [STS-1.6], в котором можно было обойти ограничение на короткую длину последовательности.

Из результатов, представленных в таблице 2, следует, что по всем 9-ти используемым тестам, последовательность партийной принадлежности Президентов США за период 18522012 гг. демонстрирует свойства случайности.

Рассмотрим более подробно тест линейной сложности, вычисленный с помощью алгоритма Берлекэмпа — Мэсси [Online Calculator of Berlekamp-Massey Algorithm], который позволяет выявить линейный регистр сдвига минимальной длины для бинарной последовательности и найти минимальный многочлен, который восстанавливает данную бинарную последовательность. С помощью Online Calculator of Berlekamp-Massey Algorithm [Online Calculator of Berlekamp-Massey Algorithm] для последовательности (табл.1) были получены следующие результаты. Linear Span (линейная сложность): 21, LFSR (линейный регистр сдвига с обратной связью): x^21 + x^19 + x^18 + x^17 + x^15 + x^11 + x^10 + x^9 + x^7 + x^4 + x^3, где «^» — знак степени. Вычисленное значение линейной сложности, приближается к n/2, где n — длина последовательности, что свидетельствуют в пользу случайности тестируемой последовательности.

Полученные результаты, подтверждают, на более надежном эмпирическом основании, как по длине последовательности, так и методам тестирования, вывод Д.Гэнса [Gans, 1985] согласно которому в последовательности партийной принадлежности Президентов США проявляются свойства случайности.

Полученные результаты свидетельствуют в пользу вывода, согласно которому бинарная последовательность (табл.1) может быть аппроксимирована распределением Бернулли с p = q=1/2, где p — вероятность принадлежности Президента США к Демократической партии, а q — вероятность принадлежности Президента США к Республиканской партии. Данный вывод следует из прохождения частотного побитового теста (табл.2), который показывает, что доля единиц близка к 0.5, а различия с наблюдаемой частотой единиц в тестируемой последовательности, которая равна 0.561, статистически незначимы (p=0,4347). Для более надежного вывода, что полученное распределение может быть аппроксимировано распределением Бернулли, автор использовал пакет EasyFit Professional [EasyFit Professional], предназначенный для автоматического анализа частотных распределений. Проведенный анализ показал, что последовательность (табл.1) наиболее точно аппроксимируется распределением Бернулли (Значение критерия Колмогорова — Смирнова равно 0.5609756, значение критерия Андерсона-Дарлинга равно 18.99698). Напомним, что распределение Бернулли возникает в схеме испытаний Бернулли — серии повторных независимых испытаний, в каждом из которых возможны два исхода, которые имеют одну и ту же вероятность, не зависящую от номера испытания.

Прогнозирование

В таблице 3 представлены результаты прогнозирования. Для регрессионных моделей и «нейронных» сетей в качестве «входа» (независимой переменной) выступали календарные даты с 1852 по 2012 гг., а в качестве «выхода» (зависимой переменной) выступали значения бинарной последовательности (табл.1). Автор не будет давать подробного описания используемых методов прогнозирования и непосредственных вычислений, поскольку этого не позволяет ограниченный объем статьи. Детальное описание используемых методов можно найти в справочных разделах используемых пакетов и в Интернете. Результаты вычислений заинтересованный читатель может получить по запросу на электронный адрес автора.

Из таблицы 3 следует, что «тест на следующий бит» пройден не был, поскольку существуют алгоритмы, которые дали корректный прогноз с вероятностью p>1/2.

Если для прогноза на 2020 г. использовать методы из табл. 3, вероятность корректного предсказания которых за 2012 и 2016 гг. составила p=1, и использовать последовательность партийной принадлежности Президентов США за период 1852

Таблица 3

Результаты прогнозирования партийной принадлежности Президентов США на 2012 и 2016 гг.

Метод прогнозирования	2012	2016	Вероятность корректного предсказания
Бинарная логит - модель (10 лагов)	+	+	1
Бинарная пробит - модель (10 лагов)	+	+	1
Авторегрессия (10 лагов)	+	+	1
Модель Кохрана-Оркатта (10 лагов)	+	+	1
Векторная авторегрессия (VAR) (2 лага)	+	+	1
SVD (Singular Value Decomposition) 5 главных компонент, которые объясняют 82,8% суммарной дисперсии	+	+	1
Тобит-модель (10 лагов)	+	-	/2
Модель Хилдрета-Лу (10 лагов)	+	-	/2
«Ксения»	-	+	/2
«Нейронная» сеть SVM	+	-	%
Вейвлет-анализ Добеши (параметр порядка -5, уровней декомпозиции - 5)	+	-

Примечания. Знаком "+" обозначен корректный прогноз, знаком "-" обозначен некорректный прогноз. 10 лагов - периодов запаздывания, что соответствует циклам продолжительностью 4,8,16,…, 40 лет. Точность аппроксимации построенных моделей колебалась в интервале 0.5-1.

— 2016 гг., то тогда прогноз будет следующим. В 2020 г. Президентом США станет республиканец. Данный прогноз дали 5 методов прогнозирования из 6 использованных. Однако, из практики прогнозирования партийной принадлежности Президентов США за 2016 г. [Pollyvote] известно, что большинство методов прогнозирования могут дать некорректный прогноз.

Обсуждение полученных результатов

Тот факт, что бинарная последовательность (табл.1) прошла тесты NIST STS (табл.2) на случайность, а используемые в данном исследовании методы прогнозирования не прошли «тест на следующий бит», является противоречием, поскольку из теоремы Э. Яо [Yao, 1982], следует, что генератор псевдослучайных чисел, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность. Наблюдаемое противоречие может быть объяснено, исходя из недостаточной длины последовательности, из ограниченного количества проведенных тестов NIST STS, приближенного характера статистических выводов о случайности, различии распределения, долей и т.д. Ниже представлено возможное объяснение, исходя из полученных в проведенном исследовании результатов.

Одним из традиционных простых тестов на случайность последовательности является анализ автокорреляционной функции. Вычисление значений автокорреляционной функции для тестируемой последовательности (табл.1) осуществлялось с помощью пакета STATISTICA [STATISTICA]. Проведенный анализ позволил выявить статистически значимое наличие лага 10 (запаздывание — цикл, продолжительностью 40 лет), значение коэффициента автокорреляции для лага 10 равно -0.329. Проведенный Фурье анализ также выявил циклы продолжительностью 24 и 40 лет. Полученные результаты, в целом, соответствуют результатам, полученным другими авторами [Merrill et al., 2008; Aguiar-Conraria et al., 2012; Norpoth, 2014] о наличии цикличности в последовательности партийной принадлежности Президентов США.

Если использовать информационные критерии для выбора порядка лагов, реализованные в пакете Gretl [Gretl], то тогда можно выделить 2 лага (цикл продолжительностью 8 лет), которые имеют минимальные значения информационных критериев Акаике (AIC) — 1.353637, Шварца (BIC) — 1.542230 и Хеннана-Куинна (HQC) — 1.412702. Данный результат согласуется с моделью Х. Норпота [Norpoth, 2014;2016], в которой учитывается доля голосов избирателей, поданных за кандидата-демократа на протяжении двух предыдущих выборов (2 лага) и которая корректно предсказала победу Д.Трампа в 2016 г.

Тестирование временного ряда на случайность также традиционно осуществляют с помощью показателя Херста [Федер, 1991: 151]. Вычисленное значение показателя Херста для бинарной последовательности (табл.1) H = 0,605597981 . Известно [Федер, 1991: 157], что если H = 0,5, то процесс является случайным, а если H > 0,5 , то такой процесс является персистентным. Для персистентного процесса характерно сохранение в будущем имеющейся тенденции к возрастанию или убыванию значений временного ряда. Отметим, что полученное значение статистически незначимо (p=0,3163) отличается от значения 0.5.

В качестве наглядной иллюстрации наличия циклов, тренда и неоднородностей в анализируемой последовательности (табл.1) на рисунке 1 представлена вейвлет-декомпозиция последовательности, выполненная в пакете Wavelet Toolbox MATLAB [MATLAB] с помощью вейвлет-преобразования Добеши с параметром порядка 5, на 5 уровнях декомпозиции.

Поскольку спектральный тест (дискретное Фурье преобразование) на случайность (табл. 2) был пройден, то выявленные циклы и тренды, полученные с помощью автокорреляционной функции, Фурье анализа и вейвлет-анализа являются незначительными.

Выше изложенные факты могут быть объяснены следую-

Рисунок 1

Вейвлет-декомпозиция последовательности партийной принадлежности Президентов США, 1852-2012 гг.

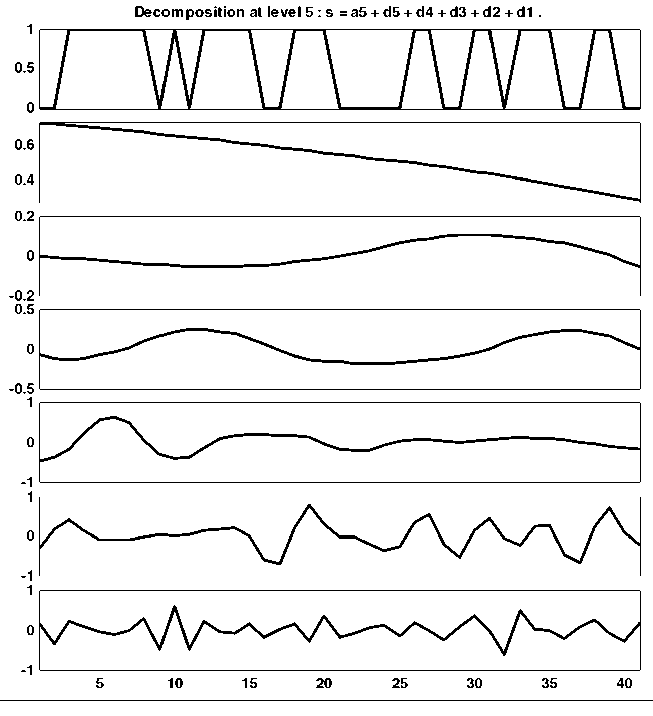
Примечания. По оси х отложены порядковые номера членов последовательности. Первый сверху фрагмент рисунка - анализируемая бинарная последовательность, второй сверху фрагмент рисунка - тренд, третий и четвертый фрагменты рисунка - циклы.

щим образом. Бинарная последовательность (табл.1) является не строго случайной, а приближенной к случайной, поскольку только демонстрирует свойства случайности и относительную независимость между членами последовательности, наличие незначительных цикличности, тренда, неоднородностей. Такие последовательности, если они генерируются детерминированным алгоритмом, в криптографии называют псевдослучайными. Кроме того, из практики моделирования случайных последовательностей, например, в экспериментах по подбрасыванию монеты, известно, что в некоторых коротких подпоследовательностях, извлеченных из длинной случайной последовательности, могут наблюдаться циклы, тренды и другие закономерности, которые наблюдались в настоящем исследовании. Используемые в проведенном исследовании методы прогнозирования (табл.3) смогли обнаружить и использовать для прогноза существующие в короткой (41 наблюдение) псевдослучайной подпоследовательности (табл.1) незначительные циклы и тренды.

Автор провел серию вычислительных экспериментов, в которых с помощью генератора псевдослучайных чисел (алгоритм Вичманна-Хилла) из пакета Microsoft Excel генерировались псевдослучайные последовательности длины n=41, по схеме испытаний Бернулли с p=q=1/2. В сгенерированных псевдослучайных последовательностях, наблюдались: p неравно g (доля единиц была заключена в интервале 0.3900.683), порядок лагов (1,4,6,8,9,11,14,16,18), тренды, показатель Херста не равен 0,5. Методы из таблицы 3 довольно точно аппроксимировали некоторые псевдослучайные последовательности и корректно предсказывали следующий элемент последовательности. Проведенные вычислительные эксперименты подтвердили, что в короткой псевдослучайной последовательности (табл.1) могут наблюдаться закономерности, которые способствуют корректному прогнозированию.

Если полученные в данном исследовании результаты, согласно которым последовательность партийной принадлежности Президентов США можно приближенно представить, как схему испытаний Бернулли с p=q=1/2, где р — вероятность принадлежности Президента США к Демократической партии, а q — вероятность принадлежности Президента США к Республиканской партии, подтвердятся на более длиной последовательности, то тогда будут наблюдаться известные закономерности случайных последовательностей. Например, согласно теореме П. Эрдеша и А. Реньи [Секей, 1990: 43], при бросании монеты n раз, серия из гербов (в нашем случае гербом — 1 обозначен республиканец, см. табл.1) длины log2n будет наблюдаться с вероятностью p, стремящейся к 1, при n, стремящемуся к бесконечности. Из данной теоремы следует, что серия из 5 непрерывных побед Президента США — республиканца, могла наблюдаться уже при 32 выборах, а серия из 6 непрерывных побед может наблюдаться при 64 выборах, что приближенно соответствует данным из таблицы 1. Таким образом, можно на основе статистической теории случайных последовательностей анализировать, объяснить и прогнозировать результаты, которые могут наблюдаться при последующих выборах Президентов США.

Если исходить из принятого в данном исследовании криптографического подхода, а также из теории социальных алгоритмов [Heise, 1995], разрабатываемой в вычислительной социологии (Computational Sociology) [Hummon, Fararo, 1995], то тогда перспективной научной задачей для последующих исследований может стать выявление генератора псевдослучайных чисел (социального алгоритма), который генерирует псевдослучайную последовательность партийной принадлежности Президентов США. Не исключено, что таким алгоритмом может оказаться один из алгоритмов детерминированного хаоса в политике [Banerjee, Ercetin, Tekin, 2014].

Выводы

Полученные результаты, подтверждают, на более надежном эмпирическом основании, как по длине последовательности, так и методам тестирования, вывод Д. Гэнса [Gans, 1985] согласно которому в последовательности партийной принадлежности Президентов США проявляются свойства случайности.

В ходе проведенного исследования было установлено, что последовательность партийной принадлежности Президентов США за период 1852-2012 гг.. может быть приближенно представлена, как последовательность псевдослучайных чисел, аппроксимированная схемой испытаний Бернулли с p=g=1/2, где p — вероятность принадлежности Президента США к Демократической партии, а q — вероятность принадлежности Президента США к Республиканской партии. Прогнозирование следующего элемента данной псевдослучайной последовательности за 2012-2016 гг. могло быть осуществлено с вероятностью корректного прогноза p>0,5. В 2020 г. Президентом США станет республиканец.