Password Hardened Biometric: A Complete Solution of Online Security

Published Online May 2013 in MECS

In present epoch protecting valuable information becomes one of the security challenges for e-businesses. Security is necessary to maintain confidentiality of important information [1]. For e-businesses to remain cut throat, strategic business partners within the systems must share secrets and move vital information during business transactions. Enterprise customers and clients involved in business-to-customer (B2C) and business-to-business (B2B) e-commerce need to believe secured and confident that their transactions are secured from system hackers.

Biometrics technology provides a solution to this problem. Biometrics technology measures physical and behavioral characteristics that are used to verify the identity of an individual [2]. The use of biometrics (e.g., fingerprints, irises, faces) for recognizing individuals is becoming increasingly popular and many applications are already available. Although these applications can be fundamentally different, they can still be grouped into one of two categories: verification and identification [3], [4], [5]. As data move between enterprise network and various systems, adequate care must be ensured to avoid systems vulnerabilities. The implementation of the biometric application programming interface [6] has made it possible for the incorporation of biometric systems into enterprise applications.

At the time of biometric acquisition, error in the form of noise is introduced by environmental conditions. The latter noise sources can be reduced or even removed by improved engineering. To solve this problem, fuzzy commitment scheme play an important role. Fuzzy commitment scheme is a tool for handling the noise in template of a biometric recognition system. Juels and Wattenberg’s fuzzy commitment scheme [7] has been introduced to handle the difference occurring between two captured of biometric data, using error correcting code.

The various approach here been proposed to protect the stored template, some are hardware based which is used stand alone biometric system-on-devices. Some are software based which is relay on feature transformation and biometric cryptosystems.

Cryptography is considered to be one of the fundamental building blocks to protect the biometric data with the growing use of biometric recognition system. Here on biometric cryptosystem common encryption technique, such as AES(Advance Encryption standard) or RSA cannot be used because of interclass variation in the biometric template[3],[4].

Common encryption technique, such as AES or RSA can’t be used, so the auxiliary data can be masked using homomorphic encryption that allows certain arithmetic operation in the encryption domain [8]. Here in this paper, we extend our work with fuzzy commitment scheme with McEliece’s cipher [9],[10] to biometric. This is also applied in online security with enhancement in the privacy of biometric cryptosystem.

Here we apply biometrics technologies in online security threats continue to spread, protecting valuable data becomes one of the security challenges businesses initial attacks it face. We will evaluate measures that can be utilized to decrease the probabilities of such attacks.

The remainder of the paper is arranged as follows. Section-II provides the background about Biometric systems and definitions of error correcting code and hamming distance. The details of the related work done previously have been discussed in section-III. Methodology for proposed system development has been discussed in section-IV. Security analysis has been done in section-V based explained system in section-IV, and conclusions have been drawn in section VI.

• B.    Definition:

A metric space is a set C with a distance function dist: C ^x C ^ R = ^[0, ” ), which obeys the usual properties (symmetric, triangle inequalities, zero distance between equal points) [13].

• C.    Definition:

Let C {0,1} ⁿ be a code set which consists of a set of code words c of length n. The distance metric between any two code words c and c in C is defined by

• II.    PRELIMINIRIES

n

dist (ci, cj) = ^ cr r =1

—

^cjr|       c i , c j &  C

• A. Biometric Systems

A generic biometric system consists of five components: Sensor, feature extractor, template database, matcher, and decision module. In general, a biometric based recognition system consists of two phase. In the enrollment phase, the biometric template b are processed from a user U and stored or registered in the database. The second phase is the verification phase; in verification system captures a new biometric sample b from U and compare it to the registered or reference data via a matching function. Let ^ be the biometric measure of ^U and ^T is a recognition threshold, ^b will be accepted if ^ ⁽ b , b ) <  ^T , else rejected. Mainly two kinds of errors are associated to this scheme: False Reject (FR), when a matching user, i.e. a legitimate user, is rejected; False Acceptance (FA), when a non-matching one, e.g. an impostor, is accepted. Note that, when the threshold increases, the FR’s rate (FRR) decreases while the FA’s rate (FAR) grows, and conversely [11].

The purpose for a biometric system configuration for positive verification ensures that the aim is the same that is enrolled in the security system as a template. Enterprise biometric template designed from a given sample is bound to an identifier by which they are known to the security system (Figure 1)

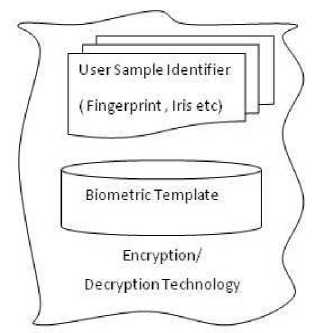
Figure 1. Component of enterprise biometric system [12]

This is known as Hamming distance [14].

• D.    Definition:

An error correction function f for a code C is defined as f (c) = {Gj / dist (c,, c) is the minimum, over C - {c }}

.

Here, Cj = f ( c ) is called the nearest neighbor of c_i [15].

• E.    Definition:

The measurement of nearness between two code words ^c and c' is defined by nearness ( c , c ' ) = dist ( c , c ' )/ n , it is obvious that 0 <  nearness (c,c') <  1 [14].

• F.    Definition:

The fuzzy membership function for a codeword C to be equal to a given c is defined as [14]

FUZZ(c') = 0        if nearness(c , c') = z < z0 < 1

= z        otherwise

• III.    RELATED WORK

The aim of this study is to provide an extension in the well known technique from the area of error correcting code and cryptography. This will help to achieve a improve type of cryptographic primitive [7], [9], [14], [15], [16], [17], [18]. On the other hand numerous works that suggest combination of biometrics and cryptography, Schneier [2] and Timmers [14] in their studies indicate that the integration of biometric technologies into applications was achieved using proprietary software developers’ kits (SDK’s).

However more recent studies summarized that a standardized biometric application programming interface, BioAPI, version 1.1 of the specification released in 2001 was association to enhance the portability of unrelated biometric technology within applications [12],[20]. Similar studies in the field of biometric security have been carried out by [21], [22], [23].

• IV.    Proposed System Architecture

Fuzzy commitment scheme is based on hash function [7] which causes them to share two shortcomings:

• 1.    The hash functions used should be strongly collision free. However, this property can only be empirically checked. It actually turns out that some schemes are inadvertently based on weakly collision-free hash functions.

• 2.    Hash functions alone cannot offer non-repudiability.

Here we use the speed of McEliece and its randomness to enhance the fuzzy commitment scheme by using code base cryptosystem which is base on Goppa Code [9], [10]. The scheme consists of three phase: first setup phase, second commitment phase and third opening/verifying phase. There are some common misconceptions about the biometric.

• 1.    Biometric authentication is the strongest authentication mechanism available.

• 2.    Biometric authentication is the most reliable authentication mechanism.

• 3.    Biometric authentication is immune to circumvention.

• 4.    Biometric technology provides a complete solution for authentication and access control.

In general, the identity theft problem is drastically exacerbated for the biometric systems.

It is to be noted that as interfaces are developed, system security could be compromised as information flows between the biometric technology, desktop, laptop or any personal computer applications.

Our main goal is to secure online access, so we protect biometric data as well as password by a cryptographic function to achieve two layer securities.

The proposed architecture of biometric system will have enhanced the security and accuracy with respect to traditional system by combine with password for online security. Figure 2 shows a flow chart that demonstrates the authentication process of a traditional password and biometric iris identification. It begins with an input iris sample. A threshold is set using a counter that is limited to two attempts for positive identification. If this process returns a negative identification, the user is prompted to contact the security administrator. If the user successfully passes the iris test for positive identification, the system prompts for a password. Another threshold is set at this stage with two attempts for a positive password. When the user has been fully authenticated with the proper password, the user will access the system.

In Biometric enrollment phase is performed during Commitment phase and verification phase is performed during open phase of fuzzy commitment scheme with McEliece cipher. At the time of enrollment phase, inputs are iris and password which is chosen randomly and public key ( ^P ) which has generating matrix that defines an error correcting code. Here g is an invertible function which maps R in to an n-bit error vector of weight ^a . The output of this phase is encrypted template and password which is stored on system.

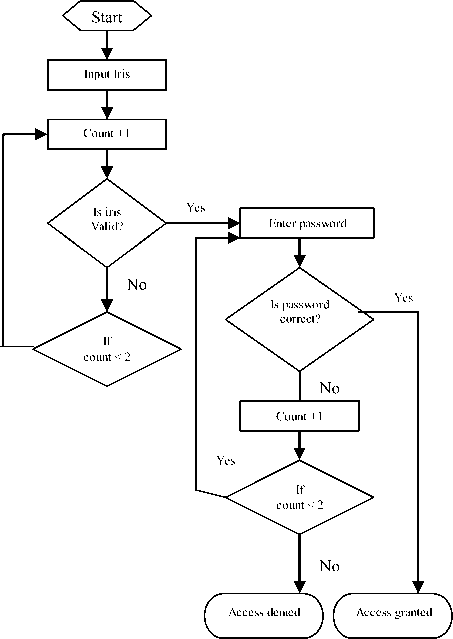
Figure 2. Authentication process of an iris and password identification

In the enrollment stage (figure3 (a)) of a typical biometric recognition system, after the biometric acquisition module, some processing is applied in order to obtain the biometric template, b which is then stored in a database and a password ( Pass ) too. Here H is called the hamming space of length N e.g. H = { 0,1 } N = F 2 N , where F 2 = { 0,1 } . Here g ‘ is an invertible function which maps R in to an n-bit error vector of weight a . However, the biometric data is never stored in the database to prevent it from being stolen. Instead, after the biometric has been acquired and the biometric template has been generated, a cryptographic function will be applied to it [10].

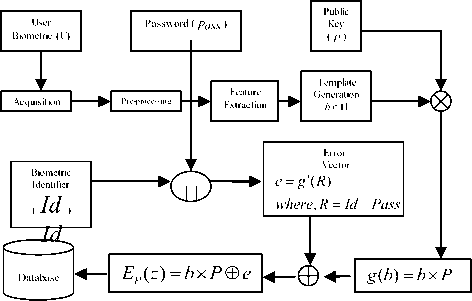
Figure 3. (a) Enrollment Phase

The result of this operation will then be stored in the database; this will be referred to in the rest of the paper as the secure biometric template. It should be pointed out that it is impossible to recover any biometric data from this secure template as the cryptographic function is not invertible.

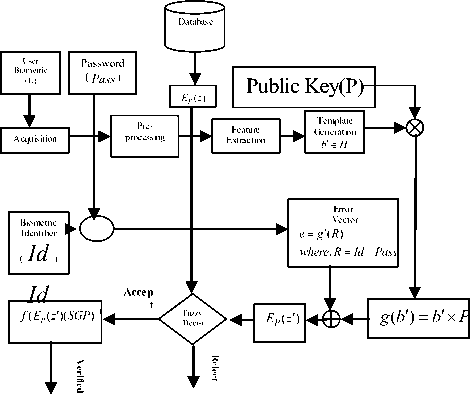
Figure 3 (b) Verification Phase

During the verification stage (figure3 (b)), the probe biometric is acquired and the corresponding template, b , is generated and enter a password ( Pass ) . The problem here is that b itself is not stored in the database, but only an encrypted version of it. To recovered the original biometric template b and password ( Pass ) from the database, if the user is who he claims, or something completely different if he is not. Therefore, the output of the feature extractor b needs to be encrypted. Only then, is the result compared to the encrypted that is stored in the database. If the E P ( z ') and E P ( z )  and password

( Pass ) are also equal then the user is validated to be who he claims to be. With this system, the three requirements above are verified. In particular, it is possible to generate many different secure biometric templates from the same biometric trait; it is just a matter of using a different set of error vector ( e ). It is also easy to cancel a secure template by simply deleting the compromised template and generating a new one by using different error vector ( e ). Finally, since the biometric data is never stored in a database, this guarantees that this information remains private.

• A.    Acquisition

  The acquisition module, absolutely necessary in a real biometric verification system, has not been implemented but here Instead of implementation, it is replaced by a large database of iris images , like the one developed by the Chinese Academy of Sciences’ Institute of Automation (CASIA) [24] and code from [25]. This database consists of 22051 iris images from more than 700 subjects. All iris images are 8 bit gray-level JPEG files, collected under near infrared illumination.

• B.    Pre-Processing

In this step after acquisition is to extract the iris from the input eye images. The iris area is considered as a circular crown limited by two circles. The iris inner (pupillary) and outer (scleric) circles are detected by applying the circular Hough transform [26], relying on edge detection information previously computed using a modified Canny edge detection algorithm [27].The eyelids often occlude part of the iris, thus being removed using a linear Hough transform [28] .The presence of eyelashes is identified using a simple threshold technique.

• C.    Feature Extraction

  Once the iris texture is available, features are extracted from it to generate a more compact representation, also called the biometric template. Reader can also read [29] in more detail, to know how Iris Recognition Works. To extract this representation, the two-dimensional normalized iris pattern is convolved with a Log-Gabor wavelet [30]. The resulting phase information is quantized, using two bits per pixel. The resulting iris template is composed of 9600 bits, stored as a 20×480 binary matrix.

• D.    Privacy-Protection and Error-Correction

In this scheme, we used McEliece cryptosystem, which add some random error at the time of encryption that makes the original template more secure than poorly chosen passwords and other cryptosystem due to its randomness.

At the time of enrollment phase, inputs are a biometric template ( b ), password ( Pass ) enter by a legitimate user, error vector ( e ) which is an invertible function that maps R = Id □ Pass in to an n-bit error vector of weight a and public key ( P ) which has generating matrix that defines an error correcting code. Here g ‘ is an invertible function which maps R in to an n-bit error vector of weight a . The output of this phase is encrypted template which one is stored on system or on a data card (i.e. smart card). Now, it is not easy to gain the template from this data without the knowledge of key and error vector.

At the time of verification phase, a similar procedure is used with a new acquire template b’ with same error vector, and key and error correction coding is used to correct biometric templates. In this stage, the probe template of a legitimate user is (error) corrected in order to recover the original template, obtained during enrollment; this should be possible because both templates are fairly similar. However, for an illegitimate user, whose probe template is fairly different from the one originally enrolled by the legitimate user, it should not be possible to recover the original from the probe template. Now we calculate f (c')(SGP) 1 and finally get the template and password. Here we also get Id and Pass of legitimate user from the R to know the identification of the machine and Pass of legitimate user to match finally. Here Id is unique for each machine so same biometric information should not be able to link template corresponding to the same individual for different machine.

Therefore, the selected error correcting code should be strong enough to correct templates of legitimate users, but not so strong as to also correct the templates of illegitimate users. Therefore, µ be the biometric measure of U and τ is a recognition threshold, b ′ will be accepted if µ ( b , b ′ ) ≤ τ , else rejected.

• V. security analysis

The accuracy of any biometric system depends on the ability of that system to separate genuine users from imposters. Here we focus on the possible attacks to the scheme [31], [32] and try to thwart them. Some issue of security in stored template consider here as:

• 1.    Stored Template should not reveal any data and no close replica made from the stored data. Poor biometric mimicry attacks implementations are vulnerable to spoofing and mimicry attacks. An artificial sample made of commercially available can deceive an iris biometric sensor.

• 2.    Multiple systems using the same biometric information (Cross-system Risk ) should not be able to link template corresponding to the same individual.

• 3.    If the stored data is compromised, remove that one and reissue a new one.

• 4.    A fraudulent user who has a similar template or characteristic to a legitimate user might deceive the system, especially in identification applications where there is a one-to-many template comparison.

• 5.    The impostor is continuously attempting to enter the system by sending incrementally increased matching data to the matching function until a successful score is accomplished.

To prevent this we have used, Goppa code in McEliece, first we encrypt a user biometric template and at the time of encryption an error vector of fixed weight α is added. To reveal any template; attacker should now the solution of decoding problem for unknown weight α of error vector which is very hard to solve. Coding theory based cryptosystem is secure because decoding is hard without the knowledge of secret.

To avoid this we can consider error vector as e = g ′ ( R ) here g is an invertible function which maps R into an n -bit error vector of weight α . Where R = Id □ Pass and Id is machine identification and Pass (password) which is a pseudo random vector. Since, each system has unique Id so same biometric information should not be able to link template in two or more applications with different security levels corresponding to the same individual.

To avoid this situation it is possible to generate many different secure biometric templates from the same biometric trait; it is just a matter of using a different set of error vector (e ). It is also easy to cancel a secure template by simply deleting the compromised template and generating a new one by using different error vector ( e ).The randomness property of error vector is also required to prevent crossmatching of subjects across databases.

It can be overwhelm the fraudulent user who has a similar template or characteristic to a legitimate user can’t match the template, due to different R Where R = Id □ Pass make the template different.

McEliece cryptosystem have randomness and probabilistic to check brute force attacks.

• VI. Conclusions

  In 1994, P. Shor gives an idea about that quantum computers will be able to break cryptosystems based on integer factorization and discrete logarithm, e.g. RSA or ECC. He explained that Code-based cryptosystems are promising alternatives to public key cryptosystems, and believed to be secure against quantum computer attacks.

In this paper we applied fuzzy commitment scheme with code base cryptosystem to achieve high speed encryption/decryption and non-repudiability, which was not available in previous hash based fuzzy commitment scheme. Further, this improved fuzzy commitment scheme used in biometric recognition system, which gives the extremely secure template due to randomness of error vector. Finally, we showed an application of this improved and password hardened biometric system for online security.

In this scheme, we used McEliece cryptosystem, which add some random error at the time of encryption that makes the original template more secure than poorly chosen passwords and other cryptosystem due to its randomness. McEliece cryptosystem is also probabilistic which give more susceptibility towards brute force attacks.

It also provides non-repudiation i.e. a legitimate user may access the facilities offered by an application and then do not claim that an intruder had circumvented the system.

In table I, II and III shows the triple values of (n, k, t), for code base system, where n denotes the codeword length, k denotes the message length and t is the error correcting capability of the code. The following equation is used to calculate the reduced entropy in table II and III.

The reduced entropy of the secret = log 2 (2^(n/k)-2^t)^k

As shown in the table no.3 proposed technique reduces the information leakage up to a remarkable level, this can improves online security and opens a new venture for the further studies.

Uniqueness of our process is that we store biometric template and password together in encrypted form both without the fusion of score level and decision level. So our proposed scheme enhances the biometric security and accuracy from the previous available literature.

Table I. (Buchmann, 2004), EFFICIENCY AND SECURITY OF THE McEliece CRYPTOSYSTEM VS RSA

CRYPTOSYSTEM

System	Size public key (bytes)	Work factor (binary operations)
		Encrypt ion/ Block size	Decrypti on/ Block size	Best Attac k
McEliece [1024, 524, 101]	67,072	29	213.25	265
RSA 362-bit Modulus	46	217	217	268
McEliece [2048, 1025, 187]	262,400	210	214.5	2107
RSA 1024-bit Modulus	256	220	220	2110
RSA 2048-bit Modulus	512	222	222	2145
McEliece [4096, 2056, 341]	1,052,672	211	215.5	2187
RSA 4096-bit Modulus	1024	224	224	2194

Table II. PREVIOUS METHOD

(n,k,t)	FRR	FAR	The reduced entropy	Information leakage
(255,239,2)	0.2533	0	255	0.0066
(255,155,13)	0.1200	0	254.99	0.0037
(255,131,18)	0.0935	0	254.99	0.0029
(511,493,2)	0.2667	0	511	0.3930
(511,457,6)	0.1667	0	511	0.3575
(511,421,10)	0.1400	0	511	0.3225
(511,184,45)	0.0533	0	510.99	0.1143

Table III. PROPOSED SCHEME

(n,k,t)	FRR	FAR	The reduced entropy	Information Leakage
(255,239,2)	0.2533	0	255	0.0066
(255,155,13)	0.1200	0	254.98	0.0036
(255,131,18)	0.0935	0	254.92	0.0028
(511,493,2)	0.2667	0	511	0.3690
(511,457,6)	0.1667	0	511	0.3520
(511,421,10)	0.1400	0	511	0.3220
(511,184,45)	0.0533	0	510.92	0.1140