Patch based image inpainting technique using adaptive patch size and sequencing of priority terms

Published Online August 2019 in MECS

Image inpainting is used to rebuild the missing area in an image. The intend of image inpainting is to fill in the absent area in an image which is unseen to human eyes. There are diverse types of image inpainting techniques such as exemplar based image inpainting, texture synthesis based image inpainting, PDE based image inpainting, hybrid inpainting and Semi-automatic and Fast Inpainting. Image inpainting is also applied for reestablishment of old images, adjustment of red-eye, object eradication in digital photographs, deletion of spots of dust in image, innovative effect by removing objects etc.

To reconstruct large textured regions Criminisi et al. [1, 2] suggested a similar patch copy and paste method. A similar patch from the surrounding known regions is searched by using similarity criteria to inpaint the missing pixels. This method involves two terms that are data term and confidence term which define the priority of the pixels to be filled first and to propagate structure as well as texture. By properly selecting similar patches the damaged region is filled by copying pixels from the corresponding similar patches i.e exemplars.

The author of reference [5] expands an exemplar based image inpainting technique by integrating Bézier curves to build missing edge information. The foundation of this technique is the contour lines restoring and exemplar based image inpainting technique with mean shift segmentation to understand color segmentation in damaged image. Then, Bézier curve is utilized to join the missing contour lines to rebuild main structure in damaged area. Finally the algorithm selects a best patch from the source to complete the inpainting procedure. Image inpainting [6] methods are classified as exemplar or non-exemplar, linear or nonlinear, isotropic or anisotropic to facilitate the propagation in particular direction which takes into account the curvature of the structure present in the nearby known areas. Non exemplar methods perform better for straight lines, curves, and for inpainting small regions and fail for recovering the texture of large areas. Multiple candidate patches are selected for each target patch using a Gaussian-weighted nonlocal texture similarity measure in [7]. Exemplar based technique [8] is improved by using adaptive size of window; the size of window is selected based on patch sparsity. Structure tensors [9] are used to enhance the filling order priority and template matching. The technique used to define similarity between patches is based on Hellinger distance[10]. Time complexity [11] is reduced by converting the global search matching algorithm into local one. Image gradient [12] is used as a similarity metric for searching similar patches. Structure sparsity based on sparseness is used to define priority function [13] with higher priority given to patch with larger structure sparsity, which is generally located at the structure, and is selected for further inpainting. A patchbased image inpainting [14] is based on variance and structure consistency between the adjacent points in the target region.

Criminisi’s algorithmic performance can be enhanced by using variable patch size [15] and confidence value is modified based on search accuracy. Inpainting [16] by separating the image into foreground and back ground using the graph cut algorithm. The foreground and back ground regions are inpainted separately with best-match patches taken from the regions respectively. The exemplar-based image inpainting [17] method is enhanced by reduced source region and modified fill front updating scheme. A multi-scale [18] patch log likelihood imposes the patch-based model on different scale patches extracted to narrow the gap to the global modeling while preserving the local treatment. A MRF-based inpainting [19] uses context-aware approach to reduce the number of possible labels per MRF node and choose them in such a way that they better fit the surrounding context. The refined patch is obtained by filtering using α (alpha)-trimmed mean filter to inpaint the target patch pixel-by-pixel. Traditional exemplarbased inpainting technique is enhanced by a patch shifting scheme [20] which provides more appropriate target patch.

• A.    Key Issues And Core Technologies In Inpainting .

The problem with most inpainting methods is they cannot proficiently reconstruct huge damage regions. In numerous patch based methods the patch width is fixed and is not adaptive to damaged area and information content in the neighborhood region. For patch based method the priority calculations are done for each iteration and more time is spent on calculation of boundary and new priority term. This can be reduced to decrease time taken by the algorithm to inpaint the entire region. The core technologies in inpainting include diffusion based, non diffusion based. Another key issue is to determine the point on the boundary of the damaged region at which the inpainting procedure is to be initiated. Also efficient evaluation methods for evaluating inpainted images is another key issue in inpainting.

• B.    Related Work And Motivation

Many authors have proposed algorithm for modification in Patch based inpainting to improve quality of inpainting and to reduce time required for inpainting. The modifications proposed by authors are in calculation of priority term, search strategy and refining multiple patches for accuracy. No attempt has been made for reducing time required for inpainting procedure using adaptive patch size and reducing priority calculations. This can be achieved by calculating the patch width based on the damaged area and the statistical properties of the neighborhood regions. Minimum patch width is selected and increased adaptively to suit the neighborhood region. This width is increased to a maximum value and then decreased based on the area to be inpainted which is iteratively updated.

Our main contributions are

• (i)    The conventional patch based technique performs well for reconstructing straight lines, but fails for reconstructing edges and corners. The patch based method involves priority calculations and matching criterion. The contribution is gradient function and curvature finding term in priority calculations. These terms identify the corners and edges and give high priorities to pixels at the edges and corners.A new equation is suggested for priority of a point on the boundary as a combination of curvature term and gradient

function with weight factors a and b .

• (ii)    Optimise the value of a and b for improved performance parameters.

• (iii)    Assigning patch width based on damaged area, statistical and spatial properties of the pixels in the neighborhood.

• (iv)    Reducing the calculation time in each iteration by sequencing the priority terms.

• II.    Background

A. Patch Based Image Inpainting

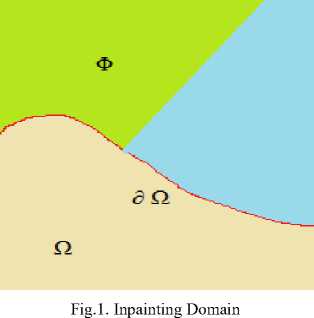
The exemplar based image inpainting is an important category of inpainting algorithms. The exemplar based image inpainting is an efficient technique of reinstallation of big target regions. Consider a region Ω to be inpainted (target region) and let ∂ Ω be its boundary between the known and unknown region and Φ is the source region as illustrated in figure 1.

The exemplar based image inpainting selects the best matching patches from the known area, whose similarity is determined by certain metrics, and insert into the target patches in the missing area. According to the filling order, the technique fills structures in the missing regions using spatial information of neighbouring regions. The exemplar based image inpainting consists of the following steps:

• 1)    Determine the Target Region by finding the damaged pixels.

• 2)    Computing Filling Priorities to determine the point on the boundary at which the filling procedure is to be initiated based on the information content of the image.

• 3)    Searching similar patches based on minimum mean squared error of the pixel values of source patch and target patch.

• 4)    Copying the most similar patch at the target region.

• 5)    Updating Image Information to proceed with the filling process by updating the boundary of the target area and filling priorities.

• III.    Proposed Algorithm

• A.    Priority Term And Its Significance

The priority term gives us an idea about the most suitable patch to be filled first around the damaged pixel ‘p’ on the border of the damage cover, (drawn/chosen by user).

There is intervention of user as image inpainting is an image editing tool. Since the patch being chosen is a square one, it is quite a possibility that next suitable patch centre lies on the square that was filled during earlier iteration, in the case where the priority is chosen based on the number of pixels known in the destination patch. Hence the patch fill order follows the previous filled patches proceeding and filling the interior of the damaged region, moving towards filling some of the borders which is not feasible in cases where image structure is to be restored. To solve this problem fill order is chosen to begin with most suitable pixel and fill the complete exterior border first and moving inwards in circular manner during the next iterations.

In this work the priority of the patch to fill is decided based on the research [26] of the patch around destination pixel ‘p’, which takes into consideration the known as well as unknown pixels of patch.

• B.    Methodology

To recover the target region (masked region) in the image the priority P_r(p) of every pixel is calculated on the boundary of damaged region. Referring to figure 2 for a patch Ψ p, δΩ is the contour of the target region, np is the normal to the contour and V Ip 1 is the isophotes (direction and intensity) where I is the entire image while Φ is the undamaged area and Ω is the damaged area. We have defined Priority as follows

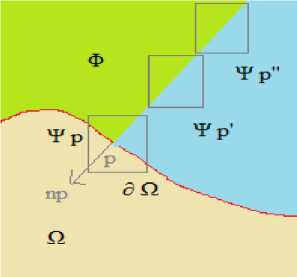
Fig.2. Patch based inpainting flow direction

PAp^ = d^ r i⁽P) + bP_r2(p)          (1)

P r i⁽P) = C_T⁽p)

D_r(p) ф ^^^^^^^^^^^^^^^^^^

2na(,Kr(p)+a)

CAp)=0 for target region, C(p)= 1 for source region

Pr2(p) = |VI|+log(|VI| + 1)(3)

«^■Ш(4)

Dr(p) =    : •

In the above equations

P r i(p) is curvature term.

P r 2(p) is gradient term.

V I is gradient of the pixel p a and b are weight factors. о and a adjustment parameter np is the normal to the contour δ Ω

VI_pL is the isophotes perpendicular to 5 fi

These values of a and b are selected as 0.4 and 0.6 respectively based on the best results obtained for SSIM for many images. о and a adjustment parameters are chosen as 0.8.

The curvature term is added to priority equation to aid the filling of pixels along the curve. Kp is curvature of isophotes (line of equal intensities) and represents geometric information of the image. α is a fine-tuning parameter for higher accuracy added in manual way. Based on type of input image this parameter can be adjusted. This factor has the capability to preserve more low-frequency contour features in the smooth areas, maintain high-frequency marginal features and also enhance medium-frequency texture details.

In patch based image inpainting the patch width w is fixed as either 5x5 or 7x7 etc. The initial value of patch width is fixed as w1

= area *

100 ^imagesize

This patch width can be made adaptive based on the damaged area and the standard deviation at the patch across highest priority. The patch width can be defined as w = w1 + rowid(1 + 2 *

(area* "00 J )  (7)

V          std(patch)/^{y v 7}

^ т (р) Values are sorted according to descending order. Let the highest priority value be H. All the priority points lying in the range of R= ( 0.96 * H, H) is determined. These priority values correspond to row column information on the boundary between known and unknown region All the values from H to 0.96*H is arranged in descending order. The patch around H is extracted and a similar patch is found from the known region using minimum value of sum squared distance.

^ qr=arg™^d(Tp-,Tq) ⁽⁸⁾

The ф_дт is the summation of squared differences of the already known pixels in the current patch and the selected patch. After finding the most suitable patch in the source region of the image copy and update the patch to the target region. And repetitively implement the above mentioned steps until all the pixel positions having priority values in the range R are exhausted. The patch width is adaptive so the new value of w is calculated using equation The algorithm is continued by finding the new boundary, new priority values and sequencing the values till the entire region is filled.

• IV.    Experiment simulation and Result Analysis

To test the algorithm we have taken original images of heritage sites. As image inpainting is an image editing tool user intervention is needed in the form of marking the region to be inpainted. In order to evaluate our algorithm we have compared our results with the basic Criminisi’s[1] algorithm, alpha trimmed filter [21], EBIIMPD [22], knnkvalpha (kn similar patches in the vicinity of damaged area with alpha trimmed filter) [24], knnsvd (kn similar patches with SVD for patch refinement) [25] and knnkvsvd (kn similar patches in the vicinity of damaged area with SVD for patch refinement). Parameters which are important in deciding the quality of an image are mean square error (MSE), luminance(L), cross correlation(XK), absolute difference (AD), normalized absolute error (NAE), structural content(SC), PSNR and structural similarity [23]. The quality factor is defined as the product of all the above listed parameters. From table 1 to 5 we see that the proposed method performs considerably better in terms of quality factor and time taken. Output image of proposed work and of other standard algorithm are as shown in figure 3 to 6.

• V.    Conclusion

In this paper we have proposed algorithm that enhances the performance of patch based image inpainting by using adaptive patch size and sequencing of the priority terms to provide faster inpainting. The patch size is made adaptive to the area of damaged region and inversely proportional to standard deviation of the known values in the patch around point at which patch priority is highest. For smooth regions patch width is large and small for structured regions. By adaptively selecting the patch width, the performance is enhanced in the form of time taken. Also sequencing of the patches reduces the over head of the algorithm in terms of calculation time and improves the speed of inpainting. In future the algorithm can be implemented by finding the priority by using standard deviation of known pixels in the neighbourhood region (wxw) of a point on the boundary.

Table 1. Performance parameter for image 1

Method	Q	SNR	SS	L	MSE	XK	NAE	AD	SC	Time
EBIIMPD[22]	34.7467	35.3991	0.9894	1.0000	0.9999	1.0005	0.9957	0.9977	0.9983	109.9101
Alpha[21]	30.4327	31.2753	0.9846	1.0000	0.9997	1.0001	0.9933	0.9971	0.9979	438.8572
Criminisi [1]	36.9477	37.3473	0.9932	1.0000	0.9999	1.0000	0.9970	0.9995	0.9996	16.8118
Proposed	34.8547	35.3963	0.9890	1.0000	0.9999	0.9997	0.9963	0.9999	0.9999	19.2942
Knnkvalpha[24]	33.9543	34.5061	0.9906	1.0000	0.9999	1.0003	0.9962	0.9984	0.9985	33.8665
knnkvsvd	22.3133	24.3050	0.9772	0.9999	0.9988	1.0075	0.9841	0.9715	0.9766	150.1212
Knnsvd[25]	32.4530	3.0775	0.9887	1.0000	0.9998	1.0003	0.9956	0.9984	0.9982	59.5980

new priority deng damaged region knnsvd knnkvalpha knnkvsvd original image

(c) tensor+w+morepoints alpha trim cnminisi

Fig.3. (a) Original image (b) Damaged image (c) New Priority deng (d) alpha trim (e) criminisi (f) Proposed (g) knnkvalpha (h) knnkvsvd (i) knnsvd

Table 2. Performance parameter for image 2

Method	Q	SNR	SS	L	MSE	XK	NAE	AD	SC	Time
EBIIMPD[22]	28.1607	29.4485	0.9841	1.0000	0.9996	0.9947	0.9887	0.9949	0.9935	93.4585
Alpha[21]	29.7969	30.9186	0.9873	1.0000	0.9997	1.0034	0.9899	0.9927	0.9902	672.7298
Criminisi [1]	28.1040	29.5340	0.9858	1.0000	0.9996	0.9929	0.9904	0.9921	0.9898	18.4781
Proposed	27.6559	29.1193	0.9818	1.0000	0.9996	0.9933	0.9893	0.9937	0.9911	24.0895
Knnkvalpha[24]	28.9223	30.2055	0.9882	1.0000	0.9997	0.9936	0.9916	0.9930	0.9907	70.9303
knnkvsvd	27.1618	28.4810	0.9834	1.0000	0.9995	1.0046	0.9883	0.9914	0.9857	183.0305
Knnsvd[25]	28.0735	29.3960	0.9844	1.0000	0.9996	0.9934	0.9906	0.9950	0.9911	63.8052

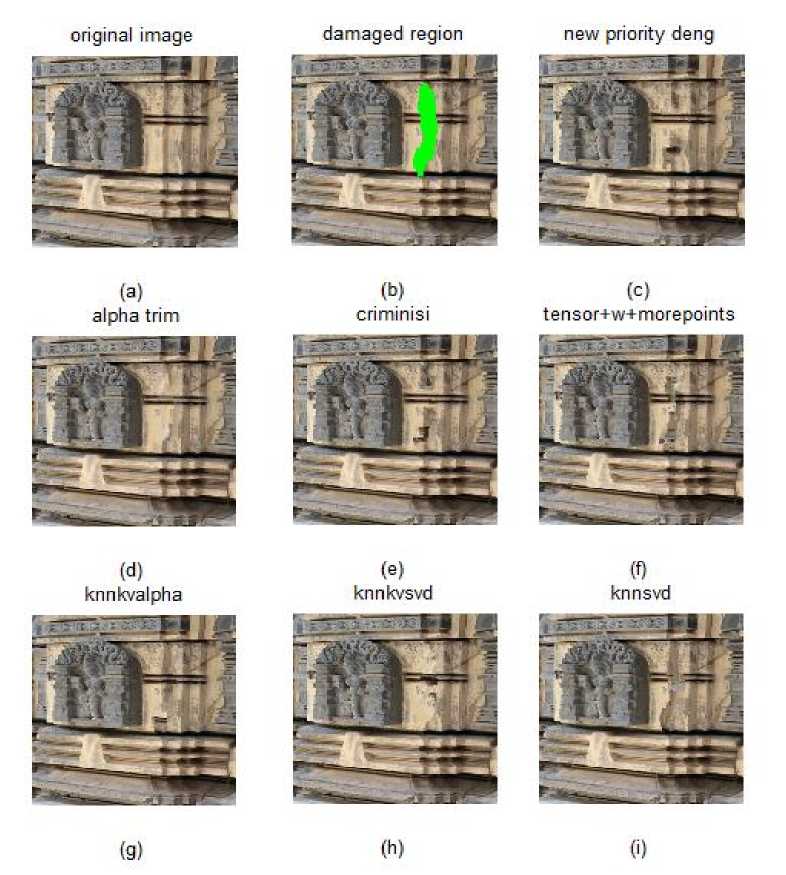
Fig..4. (a) Original image (b) Damaged image (c) New Priority deng (d) alpha trim (e) criminisi (f) Proposed (g) knnkvalpha (h) knnkvsvd (i) knnsvd

Table 3. Performance parameter for image 3

Method Q SNR SS L MSE XK NAE AD SC Time EBIIMPD[22] 29.0586 29.8532 0.9846 1.0000 0.9997 0.9976 0.9931 0.9993 0.9989 83.9353 Alpha[21] 30.4017 31.1615 0.9853 1.0000 0.9997 0.9993 0.9940 0.9985 0.9985 223.6281 Criminisi [1] 28.5547 29.3215 0.9834 1.0000 0.9996 0.9979 0.9928 1.0000 1.0000 2.7768 Proposed 30.0281 30.7953 0.9863 1.0000 0.9997 0.9975 0.9946 0.9986 0.9981 16.1227 Knnkvalpha[24] 30.3104 31.3737 0.9900 1.0000 0.9998 0.9946 0.9951 0.9943 0.9918 118.8844 knnkvsvd 30.0602 30.8452 0.9841 1.0000 0.9997 0.9980 0.9944 0.9992 0.9989 241.8245 Knnsvd[25] 29.2807 30.3988 0.9891 1.0000 0.9997 0.9941 0.9947 0.9937 0.9915 114.8519 original image           damaged region           new priority deng

(b) criminisi

(g)                            (h)                             0)

Fig.5. (a) Original image (b) Damaged image (c) New Priority deng (d) alpha trim (e) criminisi (f) Proposed (g) knnkvalpha (h) knnkvsvd (i) knnsvd

Table 4. Performance parameter for image 4

Method	Q	SNR	SS	L	MSE	XK	NAE	AD	SC	Time
EBIIMPD[22]	28.1458	29.9131	0.9708	1.0000	0.9997	0.9943	0.9886	0.9943	0.9920	114.1380
Alpha[21]	29.7396	31.1850	0.9702	1.0000	0.9997	0.9970	0.9898	0.9996	0.9966	668.2251
Criminisi [1]	30.1367	31.4838	0.9781	1.0000	0.9998	0.9960	0.9921	0.9961	0.9944	27.4373
Proposed	28.5658	30.1150	0.9704	1.0000	0.9997	0.9956	0.9904	0.9973	0.9945	37.0576
Knnkvalpha[24]	24.3450	26.7072	0.9658	1.0000	0.9993	0.9880	0.9859	0.9865	0.9829	170.6650
knnkvsvd	28.3689	29.7538	0.9681	1.0000	0.9996	0.9974	0.9896	0.9998	0.9983	373.1027
Knnsvd[25]	21.7092	24.5257	0.9620	0.9999	0.9988	0.9829	0.9810	0.9776	0.9773	115.6693

Fig. 6. (a) Original image (b) Damaged image (c) New Priority deng (d) alpha trim (e) criminisi (f) Proposed (g) knnkvalpha (h) knnkvsvd (i) knnsvd

Fig.7. (a) Original image (b) Damaged image (c) New Priority deng (d) alpha trim (e) criminisi (f) Proposed (g) knnkvalpha (h) knnkvsvd (i) knnsvd

Table 5. Performance parameter for image 5

Method	Q	SNR	SS	L	MSE	XK	NAE	AD	SC	Time
EBIIMPD[22]	29.8522	31.1932	0.9808	1.0000	0.9997	0.9948	0.9919	0.9964	0.9925	114.6434
Alpha[21]	28.1807	30.1477	0.9770	1.0000	0.9997	0.9903	0.9901	0.9919	0.9841	556.9826
Criminisi [1]	28.1612	29.6971	0.9827	1.0000	0.9996	0.9919	0.9919	0.9931	0.9879	16.8709
Proposed	30.2279	31.3796	0.9839	1.0000	0.9998	0.9955	0.9933	0.9966	0.9938	9.7320
Knnkvalpha[24]	26.6894	28.6468	0.9784	1.0000	0.9995	0.9888	0.9900	0.9907	0.9825	129.4109
knnkvsvd	29.6463	30.8050	0.9837	1.0000	0.9997	0.9953	0.9928	0.9966	0.9938	183.9258
Knnsvd[25]	24.6228	26.7727	0.9790	1.0000	0.9993	0.9854	0.9879	0.9869	0.9785	122.1882