Переборный метод разрешения неоднозначности в многошкальной фазовой радионавигационной системе

При вождении судов на опасных участках: в каналах, узкостях, шхерах и устьях судоходных рек – требуется высокоточное и оперативное навигационное обеспечение надводных объектов, осуществляемое с помощью радионавигационных систем (РНС) с береговым базированием опорных навигационных пунктов. Высокая точность таких РНС достигается за счет применения фазовых методов измерения радионавигационных параметров (РНП).

Примером РНС наземного базирования, использующей фазовые методы определения РНП, является РНС «Крабик», разработка и серийный выпуск которой с 2001 г. осуще ствляется предприятием ФГУП «НПП «Радиосвязь» (Красноярск) совместно с Сибирским федеральным университетом.

В состав РНС «Крабик» входят 3…6 опорных станций (ОС), размещенных на берегу в точках с известными координатами. РНС обеспечивает определение координат бортовых станций (БС) в дальномерном, разностно-дальномерном и комбинированном режимах определения места [1].

В настоящее время частотный план РНС «Крабик» задан следующими значениями несущих частот: f ₀ = 421 МГц – основная несущая частота; f ₁ = 421 ,01 МГц, f ₂ = 421,1 МГц, f ₃ = 422 МГц, f ₄ = 426 МГц, f ₅ = 431 МГц – вспомогательные несущие частоты. Значения фазовых сдвигов (ФС) измеряются ортогональным фазометром с ограниченными сигналами [2], выполняющим оценку ФС принимаемых сигналов по отношению к их копиям, сформированным синтезатором частоты принимающей станции. Измеренные значения ФС оказываются пропорциональными измеряемым значениям радионавигационных параметров: дальностей БС–ОС – в дальномерном режиме работы, разностям дальностей – в разностно-дальномерном режиме, разностям и суммам дальностей – в комбинированном режиме.

С целью уменьшения систематических погрешностей измерений отсчет значений ФС осуществляется на разностных (метрических) частотах РНС, получаемых путем вычитания основной несущей частоты f ₀ из значений вспомогательных частот f ₁... f ₅. В результате этого сетка метрических частот образует следующий ряд значений:

F m = ^f - ^f 0 = 10 КГЦ,

F m 2 = f 2 - f 0 = 100 кГц,

F m 3 = f 3 - f 0 = 1 МГц,              (1)

F m 4 = f . ^- f > = 5 МГц,

F m 5 = f 5 ^- f 0 = 10 МГц.

Определение РНП осуществляется на самой высокой метрической частоте F m ₅ ^, значение которой составляет 10 МГц. Диапазон однозначных измерений РНП для сигнала частоты F m ₅ соответствует длине волны данного сигнала, которая составляет около 30 м. Процедура нахождения целого числа длин волн, укладывающихся в отсчетном значении РНП, называется разрешением неоднозначности (PН) фазовых измерений.

Для PН может быть применен известный метод пересчета измерений (МПИ), описанный в [3]. Определение значения полного фазового сдвига на самой высокой метрической частоте F m ₅ осуществляется путем последовательного перехода от грубых ступеней РН к самой точной ступени, характеризующейся минимальным значением периода однозначности.

Грубые ступени PН характеризуются большими значениями длины волны l и, следовательно, большими значениями периода однозначных измерений. Согласно МПИ, переход от грубых к точным ступеням PН осуществляется с использованием соотношений

ф, = N+ф,,

N =

x,

-^L-^L-Ф, . -ф, + 0,5

X ,      ^{- 1}

где i = 1,..., m - номер текущей шкалы; m - общее число шкал, для РНС «Крабик» равное 5; [.] означает операцию выделения целой части числа; X_i - длина волны сигнала на текущей шкале; ф , - значение измеренного ФС на , -й шкале, выраженное в фазовых циклах; , - 1 - номер предыдущей шкалы с длиной волны X , ; Ф , _{- 1} - значение полного ФС, полученного на предыдущей шкале; N – значение целочисленной неоднозначности для -й шкалы; ф - значение полного ФС на текущей шкале.

Длины волн в (3) определяются по значениям метрических частот F m ₁ ^... F m ₅ как

V

X =    ,                     (4)

Fm где i = 1, ...,5 - номер метрической частоты РНС «Крабик»; V – значение скорости распространения радиосигналов.

С учетом (4) значения неоднозначно стей (3) могут быть определены следующим образом:

N =

•Ф , _ ₁ -ф , + 0,5

Использование формулы (3) или (5) совместно с (2) позволяет реализовать процедуру PН с целью нахождения полного ФС Ф ₅ для самой высокой метрической частоты РНС «Крабик» F m 5 ■ Значение полного ФС Ф ₅ впо с ледствии может использоваться для вычисления измеренных значений РНП.

Одной из серьезных проблем при разрешении фазовой неоднозначно сти в РНС «Крабик» является наличие многозначных отсчетов на самой низкой метрической частоте F m ₁ , равной 10 кГц, длина волны которой составляет 30 км. В результате этого отсчеты РНП могут быть получены в пределах 0…30 км, в то время как для рабочей зоны РНС, равной 150 км, значение двойной дальности может достигать 300 км. Для получения однозначного отсчета требуется задание априорных значений РНП с погрешностью ±15 км. Если же в качестве априорных данных вводятся координаты БС, то для определения места РНС в дальномерном режиме предельная погрешность не должна превышать ±7,5 км. Однако выполнение указанных требований не всегда осуществимо на практике.

Для получения однозначного отсчета РНП без необходимости задания априорных координат БС и изменения частотного плана РНС может быть использован переборный метод определения целого числа циклов первой метрической частоты 10 кГц для измеренного значения РНП.

Переборные методы находят применение при определении угловой ориентации по сигналам спутниковых радионавигационных систем [4–6], однако использование данных методов для решения задач определения координат объектов по сигналам многошкальных РНС в литературе освещено недостаточно.

В частности, имеется публикация [7], посвященная РНС сверхдлинноволнового диапазона, где упоминается возможность аналитического разрешения неоднозначности путем подбора целых циклов в измеренных значениях ФС, однако при этом отмечается высокая вычислительная сложность данной процедуры.

Следует отметить, что при реализации переборных методов определения угловой ориентации согласно [4–6] для выбора оптимальных значений фазовой неоднозначности используется критерий максимального правдоподобия. В связи с этим при реализации переборного метода РН для многошкальных РНС также целесообразно использовать критерий максимума функции правдоподобия.

При нормальном законе распределения погрешностей измерения ФС [8; 9] поиск максимума функции правдоподобия сводится к минимизации показателя ее экспо- ненты, называемого квадратом суммарной невязки. При независимости [10] и равноточности измерений ФС суммарная невязка Q(x, y) может быть определена по формуле

Q ⁽ x , У ) ^Ш — V ⁽ x oc, ^- x ) 2 ^{+ (} У oc, ^- У ) 2 | , ⁽⁶⁾ V i = 1 V ² )

где г = 1,..., n - текущий номер принимающей ОС; n -общее число ОС; X , - длина волны первой метрической частоты 0,01 МГц; k _{1 i} – перебираемые неоднозначности ФС на первой метрической частоте для i -й ОС; ф , , - значения ФС на первой метрической частоте; x_i , y_i – известные координаты -й ОС; x , y – координаты БС.

При использовании результатов измерений ФС на всех метрических частотах значение суммарной невязки Q ( x , y ) определяется следующим образом:

Q ( X , У ) = \ Ш L Г j '^{( к} ; ^+ф ji ) - V< x ОА - x ) ² + ( У OA - У , (7) V i = 1 j = 1 V ² )

где j = 1,...,5 - номер фазовой дорожки, заданной метрической частотой F m _j ; k_j – целочисленная неоднозначность ФС i -й станции на j -й метрической частоте; X j -длина волны сигнала j -й метрической частоты; ф j, - измеренное значение ФС для i -й ОС на j -й метрической частоте.

Для расчета суммарной невязки использовались исходные данные по координатам расстановки ОС и БС, приведенные в таблице.

При заданных значениях координат БС, приведенных в нижней строке таблицы, дальности БС–ОС1 ( R ₁ ) и БС– ОС2 ( R ₂) составляют соответственно 50 000,56 и 54 000,81 м. Значения суммарной невязки Q ( x , y ) вычислялись по выражению (7) в диапазоне дальностей R ₁ и R ₂ от 2 до 102 км с шагом 1 км, т. е. значения суммарной невязки Q ( x , y ) были вычислены в 10⁴ точках. При проведении расчетов дальности отбирались и по условиям их реализуемости, а именно: сумма полученных дальностей R ₁ + R ₂ должна быть не меньше расстояния между ОС1 и ОС2. По полученным значениям дальностей определялись координаты БС для проверяемой точки и значения дальностей для ОС3–ОС6.

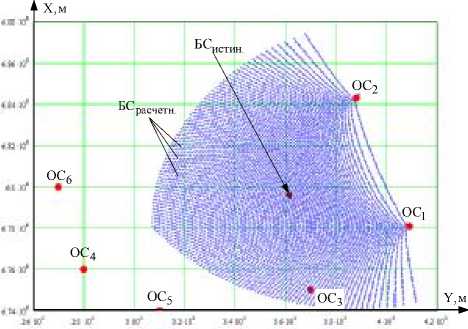
Полученная расстановка ОС, истинное положение БС и положения БС для расчета суммарной невязки приведены на рис. 1, a .

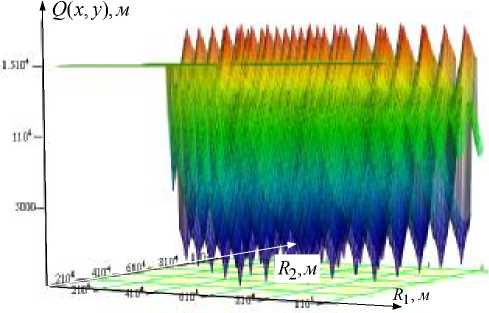
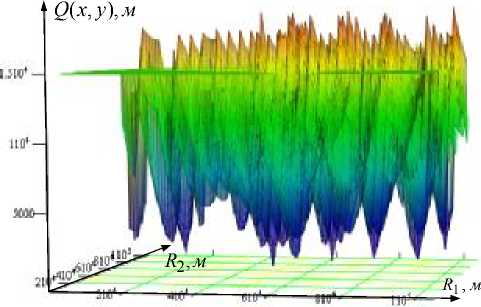
Представленные на рис. 1, б , в , г зависимости суммарной невязки от дальностей R ₁ и R ₂ позволяют сделать вывод о том, что при работе по сигналам двух ОС разрешение неоднозначности методом максимального правдоподобия невозможно, поскольку все минимумы функции правдоподобия одинаковы по своим значениям и равны нулю. С увеличением числа ОС значения суммарной невязки в побочных минимумах увеличиваются, в то время как в основном минимуме значение суммарной невязки при отсутствии погрешности измерения ФС остается постоянным и равным нулю. При этом в значении суммарной невязки при числе ОС больше двух наблюдается один минимум, соответствующий истинному положению БС (см. рис. 1, в , г ).

Следует отметить, что прямой перебор неоднозначностей на всех метрических частотах требует больших временных затрат (число перебираемых неоднозначностей составляет 104n для частоты 10 МГц в рабочей зоне 0…150 км). В связи с этим целочисленные неоднозначности kji на метрической частоте 10 кГц могут быть определены путем перебора, а на остальных метрических частотах – по МПИ независимо для каждого из РНП. В этом случае для получения отсчета потребуется анализ 121 решения, что существенно сокращает время вычисления.

Важным критерием качества алгоритмов разрешения неоднозначности является вероятность правильного разрешения неоднозначности, позволяющая судить о достоверности получаемых оценок координат объектов.

При независимости измеренных значений радионавигационных параметров вероятность правильного определения места БС находится в соответствии с выражением

P Σ = P 1 ⋅ P 2 ⋅ ... ⋅ P n ,                   (8)

где P ₁, P ₂,..., P_n – вероятности правильного РН при определении значений радионавигационных параметров; n – общее число РНП, использованных для определения места БС.

С целью упрощения дальнейшего анализа можно положить измерения фазовых сдвигов по сигналам разных ОС равноточными. В этом случае выражение (8) может быть представлено в виде

P Σ = Pⁿ ,                     (9)

поскольку P ₁ = P ₂ = ... = P_n = P .

Вероятность правильного РН при оценке одного РНП определяется в соответствии с выражением [10]:

_C 0,5 0,5 0,5 0,5

P = ₂ ⋅ ∫∫∫∫ e ^{- 0,5 ⋅ ( ∆ T ⋅ C ⋅∆ )} d Δ ₁ d Δ ₂ d Δ ₃ d Δ ₄, (10) ^{(2 π )}    - 0,5 - 0,5 - 0,5 - 0,5

а

в

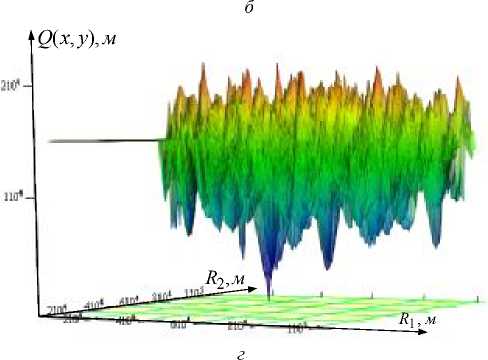
Рис. 1. Результаты расчета суммарной невязки в зависимости от координат БС:

а – расстановка БС и ОС при проведении расчетов; б – суммарная невязка, полученная по сигналам двух ОС; в – суммарная невязка, полученная по сигналам трех ОС; г – суммарная невязка, полученная по сигналам шести ОС

Координаты объектов, использованные при моделировании

Станция	Координата X , м	Координата Y , м
ОС1	6 780 852	409 077
ОС2	6 843 114	387 945
ОС3	6 750 000	370 000
ОС4	6 760 000	280 000
ОС5	6 740 000	310 000
ОС6	6 800 000	270 000
БС	6 796 062	361 446

• ^к . 2   , (И)

• ^{- к} 5 ■ ^а ф

аф- (к2 +1) , к4 = Fm4 /Fm3 ,

где C = KА-1 - матрица, обратная корреляционной матрице KА, характеризующей корреляционные связи между ступенями РН; Ai = ki ■ Афi-1 - Аф,. - погрешность РН, обусловленная погрешностями измерения ФС Аф,, и Аф;-1 на i-й и (i - 1)-й метрических частотах соответствен но.

При взаимной независимости и равноточности измерений ФС на разных метрических частотах по сигналам разных опорных станций матрица K а имеет вид [4]:

'< ( к 2 + 1) - к 3 -а ф         0

^{- к} 3 -а ф     а ф - ^{( к} 32 + 1) ^{- к} 4 -а ф

K a =

^А 0           - к 4 -а ф      а ф . ( к 42 + 1)

I 0            0         - к5 .аф где   к2 = F„2 (F^,   к3 = Fm3 [Fm ,

• ^к 5 = ^Fm ₅ / F m ₄ — коэффициенты сопряжения соседних шкал РНС; F m ₁ , F m ₂ , F m ₃ , F m ₄ , F m ₅ – значения метрических частот РНС, заданных в соответствии с выражением (1); а_ф - среднеквадратическое отклонение погрешности измерения ФС, принятое одинаковым для всех метрических частот.

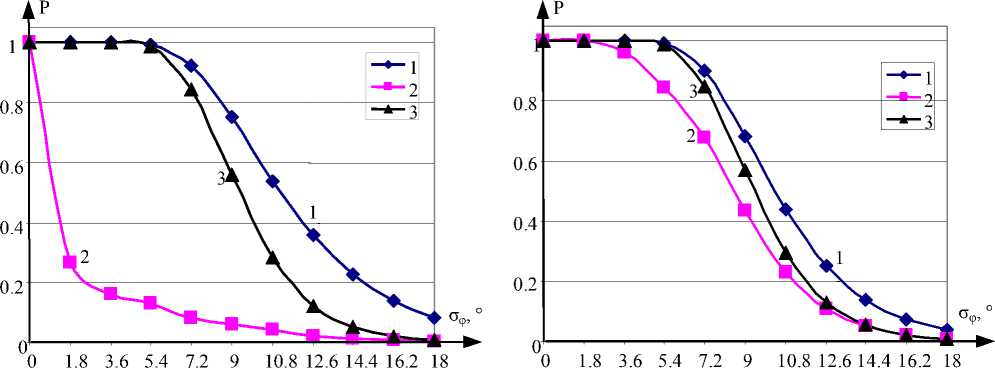
Результаты оценки вероятности правильного разрешения неоднозначно сти при определении места БС по сигналам РНС «Крабик-БМ» в зависимости от среднеквадратического отклонения погрешности измерений ФС аф для случаев работы по сигналам трех-шести ОС приведены ниже (рис. 2).

На графиках рис. 2 цифрами 1 … 3 обозначены следующие варианты РН:

• –    1 – при определении места БС при независимой оценке РНП по МПИ (при этом неоднозначность по дорожке 10 кГц считается устраненной). В этом случае вероятность определения места БС рассчитывается в соответствии с выражением (9);

• –    2 – при определении места БС во всей рабочей зоне путем перебора неоднозначностей для дорожки 10 кГц, РН для остальных метрических частот осуществляется по МПИ, выбор оптимального решения – по критерию (6);

• –    3 – то же, что и график 2, только выбор оптимального решения осуществляется по критерию (7).

Значения оценок вероятности правильного разрешения неоднозначности для графиков 2 и 3 получены методом статистического моделирования по результатам обработки 1 000 отсчетов как статистических частот P ^* , определяемых по формуле

P * = m / n , (12)

в                                                                    г

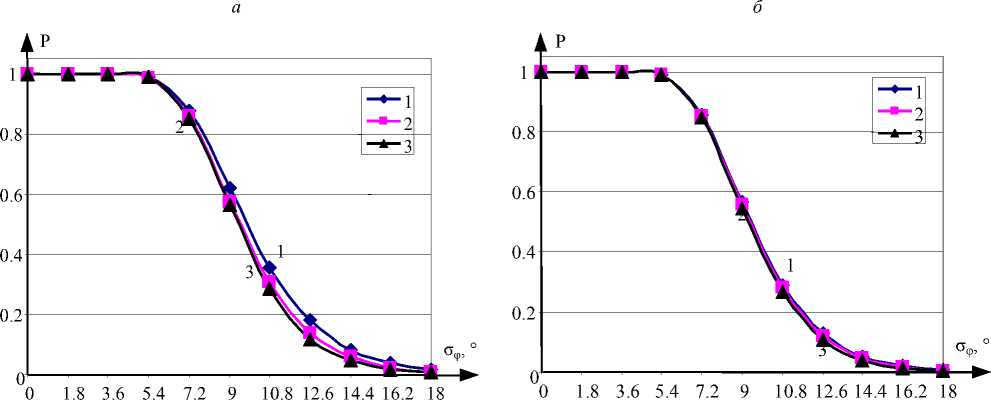
Рис. 2. Вероятность правильного разрешения неоднозначности при работе по вариантам 1–3 при работе по сигналам: а – трех ОС; б – четырех ОС; в – пяти ОС; г – шести ОС

где n = 1 000 – общее число испытаний; m – число испытаний, в которых разрешение неоднозначно сти было выполнено правильно.

Полученные результаты свидетельствуют о том, что использование при вычислении суммарной невязки Q ( x , y ) измерений ФС на всех частотах обеспечивает повышение вероятности правильного разрешения неоднозначности при малом числе ОС (четырех и особенно трех ОС). При пяти и шести ОС существенной разницы между способами вычисления невязки не наблюдается, что объясняется влиянием ошибок в разрешении неоднозначности при оценке РНП по МПИ при переходе с частоты 10 кГц на частоту 10 МГц. Использование расчета (7) по всем частотам обеспечивает повышение вероятности вследствие использования дополнительных измерений на других метрических частотах. При работе с большим числом ОС избыточность по результатам измерений имеется уже на одной метрической частоте, и при больших значениях среднеквадратической погрешности измерения ФС возникают ошибки разрешения неоднозначности по МПИ, которые влияют на результирующую вероятность правильного разрешения неоднозначности. Вероятность правильного разрешения неоднозначности по МПИ является верхней границей вероятности правильного разрешения неоднозначно сти для разработанного метода, основанного на переборе метрических частот на самой низкой метрической частоте 10 кГц.

Таким образом, полученные результаты подтверждают возможность правильного РН и однозначной оценки координат объектов в рабочей зоне РНС «Крабик». При этом не нужно задавать априорное место БС с погрешностью, не превышающей ±7,5 км, что требовалось в случае разрешения неоднозначности по МПИ. Необходимым условием реализации алгоритма является наличие избыточных ОС, используемых при определении координат БС. При этом вероятно сть правильного разрешения неоднозначности при работе по сигналам пяти– шести ОС приближается к верхней границе, задаваемой вероятностью правильного разрешения неоднозначности при независимой оценке РНП по методу пересчета измерений.

Разработанный переборный метод разрешения неоднозначности может быть использован для определения координат объектов по сигналам морских фазовых РНС с целью снижения требований к точности задания априорных координат БС. Другой областью применения данного метода является решение задач определения координат объектов в относительном фазовом режиме по сигналам спутниковых радионавигационных систем.