Передача двухкомпонентных кодов по бинарному симметричному каналу без памяти

Кодирование для канала, является важной задачей информационной системы. Оно способствует уменьшению вероятности ошибок на выходе. Одной из проблем при разработке системы передачи является выбор метода кодирования-декодирования, обеспечивающего помехоустойчивость.

На рис.1 показана, структурная схема, передачи сообщений.

Сообщения UiU2..., порождаемые источником информации, должны быть переданы получателю по каналу связи. Кодер источника, преобразует эти сообщения в последовательность двоичных символов У1І/2.... Кодер для канала образует кодовые последовательности АіАф.., способные исправлять ошибки, возникающие при передаче.

Сообщения с выхода кодера АіАф.. поступают на вход канала и передаются на вход декодера для канала в виде У1У2....

«Московский физико-технический институт (национальный исследовательский университет)», 2019

У1Т2...Уп длины п, образует последовательность У длины тхп над полем F_q. Передаваемая последовательность X и принятая последовательность У связаны соотношением, характеризующим канал связи в виде

У = X + Е,                              (1)

где последовательность Е длины т х п характеризует ошибки в канале.

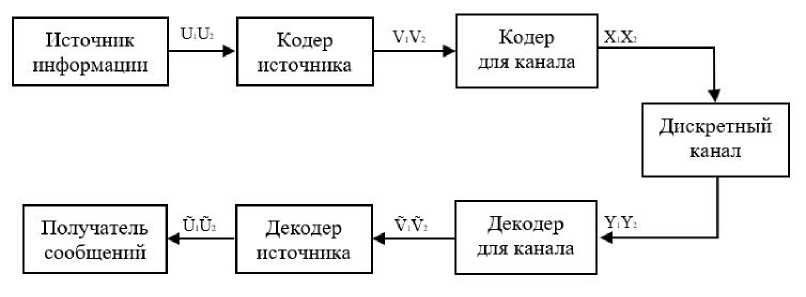
Рис. 1. Структурная схема, передачи сообщений

Задача декодера состоит в выдаче получателю сообщений. Декодер выполняет исправление ошибок. В некоторых случаях декодер может выполнять и другие функции. Например, можно построить декодер так, чтобы в надежных случаях он выдавал получателю предполагаемое сообщение, а. в сомнительных - специальный сигнал отказа, от декодирования.

Таким образом, получатель сообщений зависит от алгоритма, кодирования и характеристик канала. В этой работе используем двухкомпонентный код и бинарный симметричный канал без памяти для передачи сообщений.

Бинарный симметричный канал без памяти (БСК без памяти) характеризуется тем, что вероятность появления символа, на. его выходе определяется только набором символов на. его входе (рис. 2).

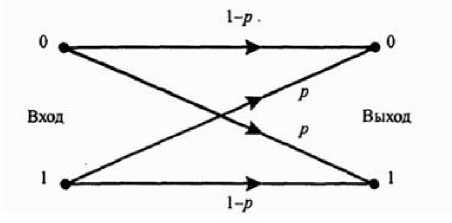
Рис. 2. Бинарный симметричный канал без памяти

Пусть q - вероятность правильного значения символа:

q = 1 - р.                                         (2)

где р - переходная вероятность (или вероятность ошибки на символе).

В случае р = 0 канал без шумов.

2.    Двухкомпонентные подпространственные коды

Двухкомпонентные подпространственные коды являются частным случаем многокомпонентных кодов с нулевым префиксом (МНП-код). Они предложены Габидулиным и

Боссертом в работах [1, 2]. МНИ коды основаны на кодах Сильвы, Кёттера, Кшишанга [3, 4], которые в свою очередь основаны на ранговых кодах Габидулина [5]. Подпространственным кодам уделяется много внимания в научных публикациях (см., например [6], [7]).

Рассмотрим двухкомпонентные подпространственные коды с параметрами (n, d, т) = (8, 6, 3).

Код состоит из 2 компонент:

* Первая компонента имеет вид: Спервый = [І3 М].

■ 10 0 М11 М12 М13 М14 М15" первый — 0 1 0 М21 М22 М23 М24 М25 0 0 1 М31 М32 М33 М34 М35 где М - матрица рангов ого кода размера 3 х 5 с ранговым расстоянием drank = dsuap2 = 3.

Мощность этого подкода равна 25.

* Вторая компонента имеет вид: Сторой = [05 І3].

С - = ^ВТороН —

0  0  0  1  00

0  0  0  0  10

0  0  0  0  01

Мощность этого подкода равна 1.

Матрица рангового кода М раз мера 3 х 5 состоит из линейного подпространства векторов размерности 5 над расширеиным полем GF (25).

Предполагается, что поле GF (25) по модулю многочлена +(ж) = ж⁵ + ж² + 1. Пусть а - корень многочлена +(ж), то есть а⁵ + а² + 1 = 0. Таблица поля имеет вид

Базисный вид	Степенной вид	Базисный вид	Степенной вид	Базисный вид	Степенной вид
0	0	1 + а4	а10	а3 + а4	а21
1	1	1 + а + а2	а11	1 + а2 + а4	а22
а	а	а + а2 + а3	а12	1 + а + а2 + а3	а23
а2	а2	а2 + а3 + а4	а13	а + а2+а3+а4	а24
а3	а3	1 + а2 + а3 + а4	а14	1 + а3 + а4	а25
а4	а4	1+а+а2+а3+а4	а15	1 + а + а2 + а4	а26
а2 + 1	а5	1 + а + а3 + а4	а16	1 + а + а3	а27
а + а3	а6	1 + а + а4	а17	а + а2 + а4	а28
а2 + а4	а7	1 + а	а18	1 + а3	а29
1 + а2 + а3	а8	а + а2	а19	а + а4	а30
а + а3 + а4	а9	а2 + а3	а20

Мощность этого подкода равна 25 = 32, поэтому существует 32 вектора рангового кода в виде т1 = (0 0 0) , m2 = (0 1  а) , m3 = (1  а а2) , т4 = (а а2  а3) , т5 = (а2  а3  а4) , т6 = (а3 а4 а5) , т7 = (а4  а5  а6) , т8 = (а5  а6  а7) , т9 = (а6  а7 а8) , т1о = (а7  а8 а9) ,тц = (а8  а9  а10) , т12 = (а9  а10  а11) , т13 = (а10  а11 а12) , т14 = (а11 а12 а13) , т15 = (а12 а13 а14) , т1б = (а13 а14 а15) , т17 = (а14 а15 а16) , т18 = (а15 а16 а17) , т19 = (а16 а17 а18) , т2о = (а17 а18 а19) , т21 = (а18 а19 а20) , т22 = (а19 а20 а21) , т23 = (а20 а21 а22) , т24 = (а21 а22 а23) , т25 = (а22 а23 а24) , т26 = (а23 а24 а25) , т27 = (а24 а25 а26) , т28 = (а25 а26 а27) , т29 = (а26 а27 а28) , тзо = (а27 а28 а29) , тз1 = (а28 а29 а30) , тз2 = (а29 а30 1) . Их матричное представление является матрицей рангового кода М:

00000 00000 М1 = 00000 М2 = 00001 00000 00010 двухкомпонентные

Таким образом, (n, d, т) = (8, 6, 3)

Мз2 = 1

подпространственные коды

с

параметрами

состоят из 33 матриц размера 3 х 8, представленных ниже. Для

краткости каждая 8-битная строка записывается как двоичное разложение числа. Например, число 129 соответствует строке [1 0 0 0 0 0 0 1]

десятичного

С = (128, 64, 32), С2

= (129, 66, 36), Сз = (130, 68,40), С4 = (132, 72,48), С5

= (136, 80, 37),

Сб =	(144, 68, 42),	С7	= (133, 74, 52),	С8	= (138, 84,45),	С9 =	(148, 77, 58),
С10 =	(141, 88, 49),	Си	= (154, 81, 39),	С12	= (145, 71,46),	С13 =	(137, 78, 60),
С14 =	(142, 92, 61),	С15	= (156, 93, 63),	С16	= (157, 95, 59),	С17 =	(159, 91, 51),
С18 =	(155, 83, 35),	С19	= (147, 67, 38),	С20	= (131, 70,44),	С21 =	(134, 76, 56),
С22 =	(140, 88, 53),	С23	= (152, 84,47),	С24	= (149, 79, 62),	С25 =	(141, 94, 57),
С26 =	(158, 89, 55),	С27	= (153, 87, 43),	С28	= (151, 75, 54),	С29 =	(139, 86, 41),

С30 = (150, 73,50), С31 = (137,82, 33), С32

(146, 65, 34), С33 = (4, 2,1).

Далее приведём описание алгоритма декодирования двухкомпонентных подпространственных кодов по минимуму Хэммингова расстояния и выполняем моделирование передачи двухкомпонентных кодов с параметрами (n, d, т) = (8, 6, 3) по БСК без памяти.

3.    Декодирование двухкомпонентных подпространственных кодовс параметрами (n,d, т) = (8, 6, 3)

Предположим, что передаваемое сообщение X на вход канале в виде последовательности. На приёмной стороне получаем последовательностью У на выходе канале в виде

У = CX ф Е,                              (3)

где С - матрица двухкомпонентного подпространственного кода в виде последовательности (С € Сі) ; Е - последовательность характеризует ошибки.

Если передана последовательность

X = (1000000001000000001000000001000000001000000001000000001000000001), тогда принятая последовательность зависит от С и Ев частности:

У = С' ф Е.                                    (4)

В этом случае можно рассматривать последовательностью С как передаваемое сообщение. Декодирования в данном случае является определено последовательности С (или М если исключим префикс). Можно написать:

У‘ = М ф Е‘,                                  (5)

где ^М е ^М і = ^{( М} і, 11 ^М і, 12 ••• ^М і, 15 ^М і, 21 ••• ^М і, 25 ^М і, 31 •" ^М і, 35 ^М і, 41 ••• ^М і, 45 ^М і, 51 •" ^Мг,55)! Е - последовательность, характеризующая ошибки.

Использован принцип декодирования по минимуму хэммингового кодового расстояния между переданным и принятым сообщениями. Декодирование двухкомпонентных кодов выполняется следующим образом: по модулю 2 сообщение У суммируем по модулю 2 с каждой кодовой последовательностью Мі,г = (1,.., 32).

Полученное последовательности после суммирования имеют вид

′′    ′

Е) — У ф Mt — M ф Е ф М і — (M ф М і ) ф Е .

Для каждой из последовательностей М і получаем поеледовательности Е). Подсчитываем число единиц в каждой сумме Е), обозначаем 8). Минимальное число единиц 8_т)_п называет соответствующую кодовую последовательность передаваемой. Есть три возможности:

I Правильные решения, если 8min соответствует передаваемой последовательности.

I Ошибка, если 8_min соответствует другой последовательности.

I Отказ от декодирования, если появилось больше одной последовательности с данным значением s_mi_n.

Вероятность соответствующих случаев называют вероятностью правильного декодирования Рцрав, вероятностью неправильного декодирования Д_Неправ и вероятностью отказа от декодирования Д_0Тказ

Дір; >,в + Дющ чяв + Дик аз — 1.

Подсчитаем число единиц в каждой из 32 последовательностей M) ,г — (1,.., 32) - j и количество последовательностей с одинаковым числом единиц Nj. Результаты приведены в табл. 1:

Таблица 1

j	0	3	4	5	6	7	8	9	10	11	12	13
N	1	3	2	3	2	4	5	3	4	2	2	1

В канале посылаем последовательность M, содержащую j единиц (j — 0, 3,...., 13). Последовательность, характеризующая ошибки в канале, является последовательность Е ' с г единицами с вероятностью С1 ₅р^г q¹⁵-¹

Предположим, что передаваемое последовательности M содержит j — 0 единиц M — M1 — (000000000000000). Такова всего одна кодовая последовательность. Отметим, что при г — 0 ил и г — 1 решения всегда правильные.

Пусть г — 2, имеем

j	0	3	4	5	6	7	8	9	10	11	12	13
8 min	2	1	2	3	4	5	6	7	8	9	10	11

Рассматриваем кодовые слова с j — 3. Когда ответ неправильный?. Если сумма содержит одну единицу ( 8 — 8_min — 1). Это значит, что две единицы последовательности из канала компенсировали две единицы в кодовой последовательности. Всего 3 последовательности. Вероятность неправильного ответа для этого случая равна

Дюправ

(2, 3) — 3С2р2 q¹³.

Для j — 4 две единицы из канала компенсировали две кодовые единицы. В сумме тоже две единицы. Событие - отказ. Вероятность отказа от декодирования для этого случая равна

Диказ^{(2, 3)} — ^2С4 ^{р q} ^.

Другие кодовые последовательности с j >  4 неправильных решений и отказов не дают при г — 2.

Проводя аналогичные расчёты для случаев г = 5, 6,..., 15, мы получаем теоретическую оценку вероятности в виде

р

1 ИСПра.В —Тсор

= ЗС2р² 913 + (ЗС3 + ЗС3 + 2С3 + ЗС3)р³91² +

+ (ЗС3 + ЗС3 + 2С4 + 2С4 + ЗС4 + ЗС³ + 2С4 + 4С4)р49^И +

+ (ЗСз ² + ЗС3 + 2С3 + 2С4 + ЗС¹ + ЗС 4 + ЗС 3 + 2С₆⁵ + 2С₆⁴ + 4С5+

+ 4С4 + 5С₈⁶ + ЗС₉>V0 + (ЗС3² + ЗС₃ ¹ + 2С3 + 2С₄⁴ + ЗС₅⁶ + ЗС₅⁴ + ЗС₅3+

+ 2С6 + 2С5 + 2С4 + 4С6 + 4С⁶ + 4С4 + 5С₈ + 5С5 + ЗС⁶ + ЗСд +

+ 4С^до + 2Сбі)р⁶д⁹ + (ЗС3² + ЗС3 + 2С3 + 2С4 + ЗС6 + ЗС6 + ЗС6 + 2С₆⁶+ + 2С5 + 2Сд + 4С7 + 4С76 + 4С⁶ + 4С7 + 5С₈ + 5С§ + 5С5 + ЗСд + ЗС⁶+

+ ЗСд6 + 4С70 + 4С6;0 + 2С73 + 2С66! + С42 + С43 )рУ + (ЗС32 + ЗС33 + 2С3+

+ 2С4 + ЗС6 + ЗС4 + ЗС3 + 2С^д + 2С6 + 2С4 + 4С77 + 4С7 + 4С₇⁶ + 4С74+

+ 5С8 + 5С7 + 5С8 + 5С^д + ЗСд + ЗСд + ЗСд + ЗС^д + 4С8о + 4С7о+

+ 4С6о + 2С81 + 2С71 + 2С61 + С182 + С^ + С83 + С^р⁸ q⁷.             (10)

Рет—тт<.< ,_Р = 2С2р² q¹³ + (2СЗ + 2С³)р391² + (2СЗ + 2С3 + 5С4)р⁴911 +

+ (2С2 + 2Сд + 5С4 + 4Сдо)р6916 + (2С3 + 2С3 + 5С4 + 4С50 + 2С62)р699+

+ (2С2 + 2Сд + 5С§ + 4С50 + 2С62)(р798 + р89? + р996) +

+ (2С2 + 2С3 + 5С4 + 4С8о)р1О96 + (2С4 + 2С3 + 5С84)р11 q4+

+ (2С2 + 2С3)р1293 + (2С2)р1293.

(И)

^Рпр а,в—т<ч >р — ^{1   Р}иеп рав—т<ч >р    ^Рет <аз—те < >р^.

Пусть вероятность ошибки в канале р от 0.1 до 0.5. Соотношение между вероятностью ошибки в канале р и теоретическими оценками РНСправ—тсоР> Рправ—теоР) Ротказ-тсор показано в таблице 2 и на рис. 3.

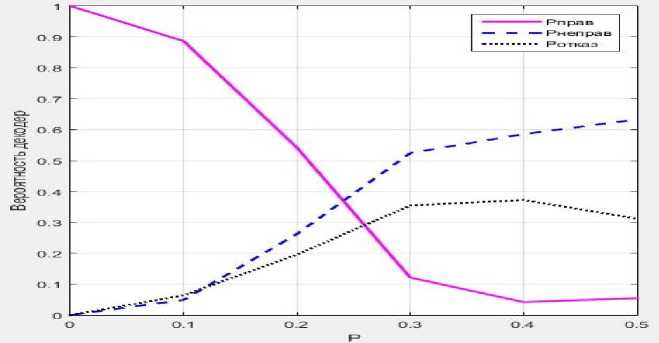
РиС. 3. ЗавИСИМОСТЬ вероятностей ^Рнсправ—тсор, ^Рправ—тсор, ^Ротказ—тсор ОТ ^р При ^М — ^М1

Таблица 2

Теоретическая оценка вероятности на основе вероятностей ошибки в канале для сообщений М = Mi

р	0	0.1	0.2	0.3	0.4	0.5
1 прав—тсор	1	0.8864	0.5416	0.1213	0.0423	0.0552
1 неправ—тсор	0	0.0495	0.2625	0.5240	0.5856	0.6326
Рот каз—тсор	0	0.0641	0.1959	0.3547	0.3721	0.3122

Анализируя получение данные, отмечаем следующее: при вероятности ошибки в канале р от 0 до 0.3 вероятность прав ильного решения Р_{прав-ТСО}р уменьшается, а вероятность ошибки Р_НСправ-тсор и вероятность отказа от декодирования Р_отказ-теор увеличиваются быстро. При р от 0.3 до 0.5, вероятность Р_{прав-теО}р продолжает уменьшаться, Р_{нсправ-теО}р увеличивается, но меньше, чем раньше; вероятность Р_отказ-теор ^в этом случае меняется мало.

Если изменим передаваемое сообщение М = М^, (г = 2, 32) и выполним пересчёт вероятности Рнсправ-теор, Pipав-тсор, Ротказ-теор, ТО ПОЛуЧИМ Следующие результаты (рис. 4).

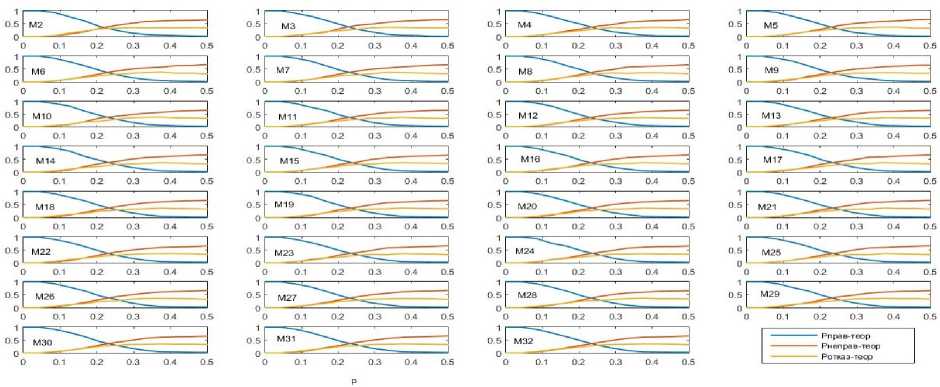
Гис. 4. Вероятности Р_ПРПрнв-_ТРОр. Р_прав-тео_Р. Р_Оті<аз-тсо_Р при М = М2,Мз2

Видим, что характер вероятности Р_нсправ— _теор, Р_прав-_тсор, Ротказ-теор не меняется при любом передаваемом сообщении М = М1,Мз2- Их среднее значение показано в таблице 3 и на рис.5.

Таблица 3

Среднее значение Р_нсправ-теор,Р_Прав-тсор,Р_Отказ-теор для различных р

р	0	0.1	0.2	0.3	0.4	0.5
1 прав-тсор	1	0.87468	0.49604	0.17224	0.043194	0.016424
1 неправ-тсор	0	0.05706	0.28106	0.50403	0.601691	0.658485
Рот каз-теор	0	0.06826	0.22290	0.32373	0.355115	0.325091

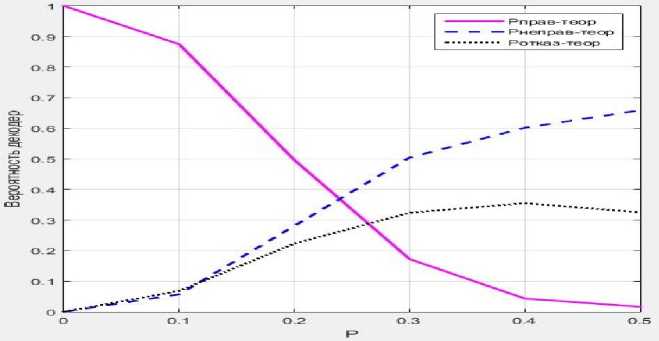
Рис. 5. Зависимость средних значений Р_нсправ-тсор,Р_прав-тсо_Р,Р_Отказ-тсо_Р ОТ вероятности р

Данные в табл. 3 и на рис. 5 можно считаем основными характеристиками для методов кодирования бинарного симметричного канала без памяти с помощью двухкомпонентных подпространственных кодов.

4.    Сравнение теоретических оценок вероятностей с результатами моделирования

Для моделирования использована программа Matlab. Структурная схема моделирования показана на рис. 6.

Рис. 6. Структурная схема, моделирования передачи двухкомпонентных кодов по БСК без памяти

При моделировании роль БСК без памяти играет генератор случайных двоичных последовательностей с заданной вероятностью символа 1 равной р (обозначение ГПЧ на рис. 6).

Определяем вероятность ошибки декодирования Р_нсп рав-модел, вероятность правильного декодирования Р_{пр ав—}модел, ВерОЯТНОСТЬ OTK аз ОТ декодирования Р_от каз —модел- Рассчитываем отношение неправильных, правильных, отказных решений к количеству де-

кодирования: Рправ—модел — к,                                  (Др Рпсправ—модел — к,                                  (ДР Роті<аз—модел = 1   Рправ—модел   Риеп рав—мо.чел,                      (До) где г - число правильных решений, t - число ошибки решений, к - количество декодирования.

В этом разделе выполнено моделирование к = 10 000 раз для каждой входной последовательности Mi, (г = 1, 32). Результаты моделирования и сравнение с теоретическими расчетами представлены в табл. 4 и на. рис. 7

Таблица. 4

Результаты моделирования и сравнение с теоретическими

р	0	0.1	0.2	0.3	0.4	0.5
1 прав—тсор	1	0.8653	0.47680	0.17580	0.03744	0.016424
1 прав—мо дел	1	0.87468	0.49604	0.17224	0.043194	0.016424
Р™™ ™___ 1 неправ—тсор	0	0.05256	0.28876	0.48053	0.58425	0.629950
Р™™ 1 неправ—модсл	0	0.05706	0.28106	0.50403	0.601691	0.658485
Рот каз—тсор	0	0.08214	0.23444	0.34367	0.36831	0.353626
Рэтказ—модсл	0	0.06826	0.22290	0.32373	0.355115	0.325091

На. рис. 7 пунктирная линия представляет вероятность моделирования, сплошная линия представляет теоретическую вероятность расчёта.

Из табл. 5 и рис. 7, отмечаем следующее: Результаты моделирования близки к теоретическим расчётам.

5.    Заключение

Здесь представлены основные характеристики декодирования, вероятность правильного сообщения, вероятность ошибки, вероятность отказа от декодирования в зависимости от вероятности ошибки на. символ в бинарном симметричном канале без памяти.

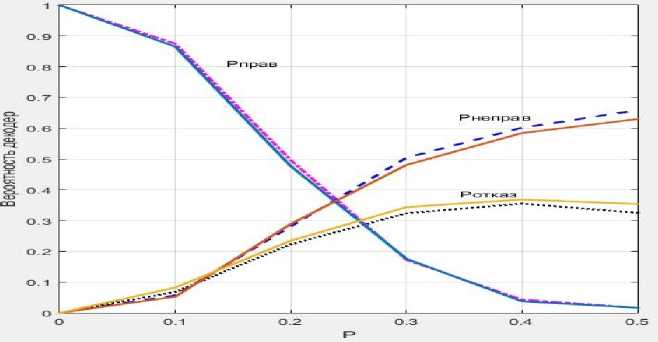
Рис. 7. Сравнение теоретических расчётов вероятностей событий и вероятностью моделирования

Проведённое исследование показывает, что двухкомпонентные подпространственные коды вполне соответствуют обычному представлению о зависимости ошибок декодирования от канала. В данном случае, чем меньше вероятность ошибки на символе в канале, тем меньше вероятность ошибок декодирования и отказов. Соответственно выше вероятность правильного декодирования.

Осуществлено сравнение теоретических расчётов вероятностей событий с результатами моделирования. Показано, что характеристики мало отличаются, а для некоторых значений практически совпадают.

Приложение

Программа моделирования вычисляет вероятность с параметром р = кер/15 при М = Мо, г де р = 0, 0.5: вероятность ошибки в канале.

Результаты ҒпрІШ-М<,Л,,л = рта;

р

1 НеПраВ — Модел

— рк^ерта'. Поп<аз—модел

= otk.

function^ra, пһерта, otk] = rankcode(kep) de;

рта = 0; пһерта = 0; otk = 0;

zero = [0 0 00 0];

a0 = [0 0 0 0 1]; a1 = [0 0 0 10];

a2 = [0 0 1 0 0]; a3 = [0 1 0 00];

a4 = [1 0 0 0 0]; a5 = xor(a2,a0);

a6 = xor(a3, a1); a7 = xor(a4, a2);

a8 = xor(a5, a3); a9 = xor(a6, a4);

a10 = xor(a7, a5); a11 = xor(a8, a6);

a12 = xor(a9, a7); a13 = xor(a10, a8);

a14 = xor(a11, a9); a15 = xor(a12, a10);

a16 = xor(a13, a11); a17 = xor(a14, a12);

a18 = xor(a15, a13); a19 = xor(a16, a14); a20 = xor(a17, a15); a21 = xor(a18, a16); a22 = xor(a19, a17); a23 = xor(a20, a18); a24 = xor(a21, a19); a25 = xor(a22, a20); a26 = xor(a23,a21); a27 = xor(a24,a22); a28 = xor(a25, a23); a29 = xor(a26, a24);

a30 = xor(a27, a25);

% 32 матрицы кодер Mi=bi (г=0,.. . ,31) b0 = zeros(3, 5); М = [a0; a1; a2];

b2 = [a1; a2; a3]; b3 = [a2; a3; a4];

b4 = [a3; a4; a5]; b5 = [a4; a5; a6];

b6 = [a5;a6;a7]; b7 = [a6;a7;a8];

b8 = [a7; a8; a9]; b9 = [a8; a9; a10];

b10 = [a9; a10; a11]; b11 = [a10; a11; a12];

b12 = [a11; a12; a13]; b13 = [a12; a13; a14];

b14 = [a13; a14; a15]; b15 = [a14; a15; a16]; b16 = [a15; a16; a17]; b17 = [a16; a17; a18]; b18 = [a17; a18; a19]; b19 = [a18; a19; a20]; b20 = [a19; a20; a21]; b21 = [a20; a21; a22]; b22 = [a21; a22; a23]; b23 = [a22; a23; a24]; b24 = [a23; a24; a25]; b25 = [a24; a25; a26]; b26 = [a25; a26; a27]; b27 = [a26; a27; a28]; b28 = [a27; a28; a29]; b29 = [a28; a29; a30]; b30 = [a29; a30; a0]; b31 = [a30; a0; a1];

% передаваемое сообщение X

X = b0;

% сделано 10000 раз fori = 1:1: 10000

% ГПЧ с вероятностью p=k/15

S = randn(3, 5) >= 0;

Ғ = snm((snm(S))’);

k = det(F );

mhilek = key

S = randn(3, 5) >= 0;

k = det(sum((sam(S ))‘));

end

% сообщений получатель

Y = xor(X,S );

% декодировано

M 0 = xor(Y, b0);M 1 = xor(Y, 51);

M 2 = xor(Y, b2);M 3 = xor(Y, b3);

M 4 = xor(Y, b4);M 5 = xor(Y, b5)

M 6 = xor(Y, b6);M 7 = xor(Y, b7)

M 8 = xor(Y, b8);M 9 = xor(Y, b9)

M 10 = xor(Y, b10); M 11 = xor(Y, b11);

M 12 = xor(Y, b12) M 13 = xor(Y, Ь 1з);

M 14 = xor(Y, b14); M 15 = xor(Y, b15);

M 16 = xor(Y, b16); M 17 = xor(Y, b17);

M 18 = xor(Y, b18); M 19 = xor(Y, b19);

M 20 = xor(Y, b20); M 21 = xor(Y, b21);

M 22 = xor(Y, b22); M 23 = xor(Y, b23);

M 24 = xor(Y, b24); M 25 = xor(Y, b25);

M 26 = xor(Y, b26); M 27 = xor(Y, b27);

M 28 = xor(Y, b28); M 29 = xor(Y, b29);

M 30 = xor(Y, b30); M 31 = xor(Y, b31);

% Подсчитано число единиц в касисдой сумме

F 0 = sum((sum(M 0))’);

F 1 = sum((sum(M 1))’);

Ғ 2 = sum((sum(M 2))’);

Ғ 3 = sum((sum(M 3))’);

Ғ 4 = sum((sum(M 4))’);

Ғ 5 = sum((sum(M 5))’);

Ғ 6 = sum((sum(M 6))’);

Ғ 7 = sum((sum(M 7))’);

Ғ 8 = snm((snm(M 8))’);

Ғ 9 = snm((snm(M 9))’);

Ғ 10 = snm((snm(M 10))’);

Ғ 11 = snm((snm(M 11))’);

Ғ 12 = snm((snm(M 12))’);

Ғ 13 = snm((snm(M 13))’);

Ғ 14 = snm((snm(M 14))’);

Ғ 15 = sum((sum(M 15))’);

Ғ 16 = snm((snm(M 16))’);

Ғ 17 = snm((snm(M 17))’);

Ғ 18 = snm((snm(M 18))’);

Ғ 19 = snm((snm(M 19))’);

Ғ 20 = snm((snm(M 20))’);

Ғ 21 = snm((snm(M 21))’);

Ғ 22 = snm((snm(M 22))’);

Ғ 23 = snm((snm(M 23))’);

Ғ 24 = snm((snm(M 24))’);

Ғ 25 = snm((snm(M 25))’);

Ғ 26 = snm((snm(M 26))’);

Ғ 27 = snm((snm(M 27))’);

Ғ 28 = snm((snm(M 28))’);

Ғ 29 = snm((snm(M 29))’);

Ғ 30 = snm((snm(M 30))’);

Ғ 31 = snm((snm(M 31))’);

% Результаты

Ғ = [Ғ0; Ғ 1; Ғ 2; Ғ 3; Ғ 4; Ғ 5; Ғ 6; Ғ 7;

Ғ 8; Ғ 9; Ғ 10; Ғ 11; Ғ 12; Ғ 13; Ғ 14; Ғ 15;

Ғ 16; Ғ 17; Ғ 18; Ғ 19; Ғ 20; Ғ 21; Ғ 22; Ғ 23;

Ғ 24; Ғ 25; Ғ 26; Ғ 27; Ғ 28; Ғ 29; Ғ 30; Ғ 31];

Z 1 = mгn(F );

t = 0;

for г = 1 : 1 : 32

if Ғ(г) == Z 1

t = t + 1;

end end if t == 1

if Z 1 == Ғ (1)

pra = pra + 1;

else nhepra = nhepra + 1;

end else otk = otk + 1;

end end