Передача орбитального углового момента асимметричных пучков Лагерра-Гаусса диэлектрическим микрочастицам

Моды Лагерра–Гаусса (ЛГ) являются точным решением параксиального уравнения Гельмгольца и представляют собой световые поля с радиально-симметричной формой поперечного сечения, не меняющейся при распространении в пространстве. Моды ЛГ нашли применение в таких областях, как оптическое манипулирование микрообъектами, квантовая оптика, оптические коммуникации. Несмотря на большое количество публикаций о модах ЛГ, их свойства исследуются до сих пор [1–9]. Так, в [1] формируются суперпозиции мод ЛГ в виде массивов одиночных или парных тёмных пятен, расположенных на световых кольцах. В [2] исследуется физический смысл радиального индекса мод ЛГ, а в [3] – их острая фокусировка. В [4] рассматривается непараксиальное распространение мод ЛГ в присутствии апертуры, а в [5] – свойства световых полей, обладающих ОУМ и не имеющих радиальной симметрии, в присутствии гармонического потенциала. В [6] предлагается метод формирования мод ЛГ в резонаторе твёрдотельного лазера. В [7] показано, что при использовании моды ЛГ вместо обычного Гауссова пучка уменьшается доплеровская ширина линии в спектре поглощения атомов рубидия-85 и рубидия-87, а в [8] рассматривается применение мод ЛГ для уменьшения влияния теплового шума в детекторах гравитационных волн. В [9] исследуется использование мод ЛГ для организации спин-орбитального взаимодействия в ультрахолодных атомах.

Наряду с изучением пучков ЛГ, продолжаются исследования применимости различных видов лазерных пучков для оптического управления микрообъектами.

В [10] предложена оптическая ловушка одновременно прозрачных и поглощающих частиц в воздухе с помощью одного структурированного лазерного пучка. В [11] сравнивается стабильность оптических ловушек на основе встречных и четверных (quadruple) пучков Бесселя (пар встречных пучков, распространяющихся перпендикулярно друг другу) и показано преимущество последних. В работе [12] мода Лагерра–Гаусса используется для создания канала транспортировки атомов, покидающих магнитооптическую ловушку, на расстояние 30 см. По сравнению со свободно распространяющимся атомным пучком его расходимость была уменьшена с 40 до 3 мрад.

В [13, 14] c помощью комплексного смещения получены асимметричные бездифракционные моды Бесселя и Бесселя–Гаусса, а в работе [15] с их помощью осуществлён захват и перемещение полистироловых микрошариков. В работе [16] аналогично, пользуясь приёмом комплексного смещения в декартовых координатах, теоретически и экспериментально исследуются асимметричные пучки ЛГ. Подобно стандартным пучкам ЛГ, их распределение интенсивности в поперечной плоскости состоит из конечного числа световых колец, но распределение интенсивности на кольцах неравномерное. При больших параметрах асимметрии пучок имеет форму полумесяца, который при распространении вращается. Пучки в виде полумесяца используются для оптического захвата и перемещения живых клеток без их теплового повреждения [17]. Аналитически рассчитан нормированный орбитальный угловой момент (ОУМ) пучка ЛГ. Он линейно зависит от топологического заряда пучка и квадратично зависит от параметра асимметрии. В данной работе получено выражение для плотности ОУМ асимметричных пучков ЛГ. С помощью оптического захвата и перемещения полистироловых шариков диаметром 5 мкм в фокусе асимметричного пучка ЛГ доказано, что скорость движения шариков растёт при увеличении параметра асимметрии и постоянном топологическом заряде, причём скорость оказывается больше, чем в асимметричных пучках Бесселя– Гаусса [15].

1. Свойства асимметричных пучков Лагерра–Гаусса

При распространении в свободном пространстве на произвольном расстоянии z комплексная амплитуда смещённого пучка ЛГ имеет вид:

E ( x , У , z ) =

w ( z ) I w ( z )

1 n

■ X

^x [ ( x - x о )⁺ i ( y ^- y о )^{1 n} L m

X exp

где

A ( p , e ) = C о p ⁿ exp

(kw p )2

-^x   )- + in e

X

2 p ² w ^{2 (} z )

X

_ p ^{2      ik} p ²

w ² ( z )   2 R ( z )

^^^^B

i ( n + 2 m + 1 ) Z ( z ) ,

p ² = ( ^{x - x} 0 ) ^{2 +} ( У ^- У 0 ) ²

R ( z ) = z

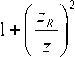
, w ( z ) = w 1 +

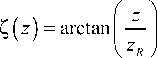
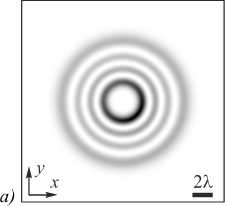
где ( x, y, z ) и (r, ф , z ) - декартовы и цилиндрические координаты, ( x 0 , y 0 ) – комплексные координаты смещения центра пучка ЛГ, w – радиус перетяжки Гауссова пучка, n - топологический заряд оптического вихря, L m ( x ) -присоединённый многочлен Лагерра, z R = kw ²/2 – расстояние Рэлея, к = 2 n / X - волновое число света с длиной волны X . В поперечном сечении интенсивность такого пучка не имеет радиальной симметрии, как у обычных пучков ЛГ [18]. Степень асимметрии зависит от параметров x 0 /w и y 0 /w . На рис. 1 показаны распределения интенсивности в плоскости z =0 для аЛГ-пучков при следующих параметрах: длина волны X =532 нм, радиус перетяжки w = 2 X , индекс пучка ( m , n ) = (3,5), поперечные смещения x 0 = 0,01 wi и y 0 = 0,01 wi (рис. 1 а ), x 0 = 0,05 wi и y 0 = 0,05 wi (рис. 1 б ), x 0 = 0,1 wi и y 0 = 0,1 wi (рис. 1 в ), x 0 = 0,2 wi и y 0 = 0,2 wi (рис. 1 г ), x 0 = 0,5 wi и y 0 = 0,5 wi (рис. 1 д ), x 0 =2 wi и y 0 = 2 wi (рис. 1 е ). Размер расчётной области равен 2 R , где R = 10 X .

Из рис. 1 видно, что все эти пучки имеют разный вид – почти радиально симметричные световые кольца на рис. 1 а , световой полумесяц, окружённый периферийными кольцами (на рис. 1 б и в) полумесяц с разорванными периферийными кольцами (рис. 1 г ), полумесяц без периферийных колец (рис. 1 д ) и эллиптическое световое пятно (рис. 1 е ).

Проекция ОУМ на ось z смещённого пучка Лагер -ра–Гаусса (остальные проекции для параксиальных пучков равны нулю) удобно искать через угловой спектр плоских волн:

J z =- i X ²f A A* | A p d p a e . (3)

" de

Для пучка ЛГ (1), смещённого на расстояния x 0 и y 0 вдоль координат x и y , выражение для углового спектра плоских волн имеет вид:

( kw p ) ²

exp | - ik p ( x ₀ cos e + y ₀ sin e ) 1 .

X L m

б)

д)

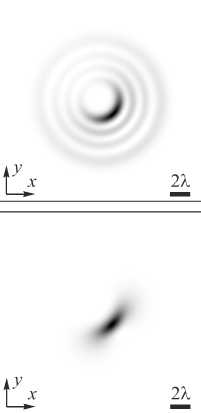
Рис. 1. Распределения интенсивности в плоскости z = 0 для асимметричных пучков ЛГ при следующих параметрах: длина волны X = 532 нм, радиус перетяжки w = 2 Х , индекс пучка (m, n) = (3, 5), поперечные смещения x 0 = 0,01wi и y 0 = 0,01wi (а), x 0 = 0,05wi и y 0 = 0,05wi (б), x 0 = 0,1wi и y 0 = 0,1wi (в), x 0 = 0,2wi и y 0 = 0,2wi (г), x 0 = 0,5wi и y 0 = 0,5wi (д), x 0 = 2wi и y 0 = 2wi (е)

Подставим (4) в (3) и получим:

т ,Л7 2 Im (x0 y0)

Jz = nW +---^--- X w2

L ¹ m

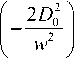
L m

+

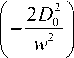
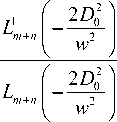
^^^^B

W ,

где

D 0 =V( Im x 0 ) 2 ⁺( Im y 0 ) ² .

Мощность W в (5) выражается через амплитуду спектра плоских волн в виде:

W = U E * E d x d y = X ² JJ A* A d a d p ,

ℝ2

ℝ2

где a и в - декартовы координаты в спектральной плоскости.

Подставив в (7) выражение (4), получим:

п w ² ( m + n ) !

W =-------x

2 m !

( f 2 =350 мм ) и L 3 ( f 3 = 150 мм) направлялся во входное отверстие микрообъектива MO 2 (40^×, NA=0,65). Изоб-

^x exp I       I L m + n

I w I

2D"

0 w ²

L

m

2D"

0 w ²

где L_m ( ^ ) = L_m ( ^ ) . В частном случае при смещении

пучка на вещественные расстояния параметр D 0 становится равным нулю и мощность (8) принимает значение [ п w ²/2][( m + n )!/ m !], совпадающее с выражением из [18]. Из (5) видно, что нормированный ОУМ (ОУМ на один фотон) J z /W не зависит от длины волны, а линейно зависит от топологического заряда n и произведения параметров асимметрии x 0 / w и y 0 / w . При | x 0 / w |= | y 0 / w |= c ОУМ в (5) зависит от квадрата параметра асимметрии c. Можно показать, что увеличение или уменьшение нормированного ОУМ полностью определяется знаком величины Im( x ₀ ^* y ₀) , так

ражение плоскости манипулирования проецировалось на матрице CMOS камеры LOMO TC-1000 (разрешение – 1280×960 пикселов, размер пикселя – 1,67 мкм) с помощью микрообъектива MO 3 (16^×, NA=0,4). Для подсветки области захвата использовалась система, состоящая из конденсора C и освещающей лампы I , свет от которой вводился с использованием делителя пучка BS . Для манипулирования в эксперименте были использованы микросферы полистирола диаметром 5 мкм, которые находились на стеклянной пластинке P , радиус Гауссова пучка w = 1 мм.

как выражение в квадратных скобках (5) всегда больше или равно 1. Заметим, что для всех пучков на рис. 1 нормированный ОУМ J z /W , рассчитанный по формулам (5) и (8), должен быть равен 5. При численном расчёте с помощью интегралов (3) и (7) он оказался равен 4,999 (рис. 1 а - г ) и 4,998 (рис. 1 д , е ).

Можно также найти плотность ОУМ для аЛГ-пуч-ка при m =0 и x 0 = aw , y 0 = iaw :

J_z = Im ^ E *,

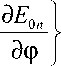
= I E 0 n ( x, У, z

,    z„x + zy I n + kaw—---2"" I, z + ZR )

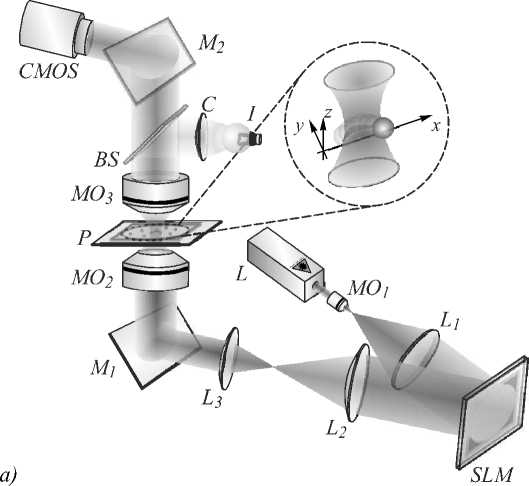
где a – параметр асимметрии, | E 0 n ( x , y , z )|² – распределение интенсивности аЛГ-пучка (1). В отличие от полного ОУМ (5), который пропорционален квадрату параметра асимметрии a ², плотность ОУМ (9) зависит от a линейно .

2. Экспериментальное исследование оптического захвата микрочастиц и передача им орбитального углового момента от асимметричного пучка

Лагерра–Гаусса

Далее мы экспериментально покажем, что ОУМ, который аЛГ-пучок передает микрочастице и который пропорционален скорости движения микрочастицы, также почти линейно зависит от параметра асимметрии a . Схема эксперимента по манипуляции микрочастицами с помощью асимметричных пучков ЛГ с линейной поляризацией показана на рис. 2. Выходной пучок твердотельного лазера L ( X =532 нм, максимальная выходная мощность – 1500 мВт) расширялся с помощью системы, состоящей из микрообъектива MO 1 (8^×, NA=0,3) и линзы L 1 ( f 1 =250 мм). Расширенный лазерный пучок направлялся на дисплей пространственного модулятора света SLM (PLUTO VIS, разрешение – 1920 × 1080 пикселов, размер пикселя – 8 мкм). Отражённый от модулятора модулированный лазерный пучок с помощью системы линз L 2

Рис. 2. Схема эксперимента для исследования передачи ОУМ микросферам полистирола с использованием асимметричных пучков ЛГ: L – твердотельный лазер (λ = 532 нм, мощность – 1500 мВт), MO 1 – микрообъектив (8˟, NA = 0,3), L 1 , L 2 и L 3 – линзы с фокусными расстояниями (f 1 = 250 мм, f 2 = 350 мм, f 3 = 150 мм), SLM – пространственный модулятор света PLUTO VIS (разрешение 1920 × 1080 пикселов, размер пикселя – 8 мкм), MO 2 – микрообъектив (40˟, NA = 0,65), P – стеклянная пластинка со взвесью микросфер полистирола, MO 3 – микрообъектив (16˟, NA = 0,4), CMOS – видеокамера LOMO TC-1000 (разрешение – 1280 × 960 пикселов, размер пикселя – 1,67 мкм), C – конденсор, I – освещающая лампа, BS – делитель пучка. Показан асимметричный пучок ЛГ (негатив) (б), сформированный SLM при следующих параметрах: w 0 = 1 мм, n = 8, x 0 = 0,2w 0 , y 0 = 0,2w 0 i, размер кадра – 2 × 2 мм

В зависимости от параметра комплексного смещения x 0 сформированного асимметричного SLM пучка ЛГ в ходе экспериментов наблюдалось либо вращение

микросфер полистирола вдоль сформированного светового кольца с асимметричным распределением интенсивности (при значениях x 0 <  0,3 w ), либо перемещение захваченных микросфер вдоль сформированной световой кривой в форме полумесяца (при значениях x 0 ≥ 0,3 w ). Когда частица движется по длинной траектории (при x 0 < 0,3 w ), на неё действует сила, пропорциональная плотности ОУМ (9). А когда частица движется по короткой траектории (при x 0 ≥ 0,3 w ), на неё действует сила, которая пропорциональна усреднённому по траектории (полному) ОУМ (5).

Попав в область аЛГ-пучка, микросфера начинает испытывать действие силы, которая прямо пропорциональна ОУМ пучка. Под действием этой силы, а также силы, возникающей из-за градиента интенсивности, микросфера начинает двигаться равноускоренно вдоль сформированной световой кривой. Чем больше плотность ОУМ, тем большее ускорение получает микросфера при движении в аЛГ-пучке. При достижении равновесия сил, приводящих частицу в движение, и сил трения и сопротивления жидкости, действующих на микросферу, она перестаёт двигаться равноускоренно и начинает двигаться равномерно.

На рис.3 показаны кадры вращения трёх микрочастиц в фокусе асимметричного пучка ЛГ параметрами асимметрии x 0 =0,1 w =– iy 0 ( n =3). Средняя линейная скорость вращения частиц в пучке после установления равновесия всех сил равнялась 0,45±0,02 мкм/с (рис.3).

Рис. 3. Распределение интенсивности в области манипулирования (крайний левый кадр) и стадии движения трёх микросфер полистирола, захваченных с помощью асимметричного пучка Бесселя с параметрами n = 3, x 0 = 0,1w = –iy 0

Типичные результаты экспериментов с использованием асимметричных пучков ЛГ с параметром x 0 = 0,4 w = – iy 0 показаны на рис. 4.

Как видно, неподвижная микросфера полистирола, попав в область пучка, ускоряется и перемещается вдоль световой кривой, сформированной в плоскости захвата (средняя скорость перемещения равна 0,84 ± 0,04 мкм/с). Следует отметить, что аЛГ-пучки формировались с помощью фазового модулятора SLM, от которого отражалась одинаковая часть энергии для пучков с разным параметром асимметрии a . Но только часть всей отражённой энергии попадала в область фокуса, где захватываются микросферы. Причем, чем больше асимметрия аЛГ-пучка, тем меньше энергии после модулятора попадает в область фокуса.

а)

б)

д)

Рис. 4. Распределение интенсивности в области манипулирования (крайний левый кадр) и стадии движения микросферы полистирола, захваченной с помощью асимметричного пучка Бесселя с параметрами n = 3, x 0 = 0,4w = –iy 0

Так, эффективность формирования аЛГ-пучка, представленного на рис. 4, в 1,8 раза меньше эффективности формирования пучка на рис. 3. И, тем не менее, скорость движения микросферы по более короткой траектории (рис. 4) почти в 2 раза больше, чем по длинной траектории (рис. 3).

В табл. 1 приведены рассчитанные значения отношения ОУМ пучков с различными параметрами x 0 / w = – iy 0 / w к ОУМ пучка с параметром x 0 = 0 ( n = 3).

Табл. 1. Рассчитанные по формулам (5), (6) отношения нормированных ОУМ асимметричных пучков ЛГ с параметрами x 0 /w = 0; 0,1; 0,2; 0,3; 0,4 и 0,5 к ОУМ асимметричного пучка ЛГ с параметром x 0 = 0 (n = 3)

x 0 / w = = – iy 0 / w	0,0	0,1	0,2	0,3	0,4	0,5
J z / W z        x 0
Jz / W z           x 0 = 0	1,00	1,03	1,10	1,19	1,31	1,43

Для экспериментального подтверждения наличия данной зависимости были проведены эксперименты с асимметричными пучками ЛГ с теми же параметрами. Мы вычисляли скорость и ускорение микросферы, которое она приобретала спустя некоторое время t после начала движения до того момента, пока движение частицы ещё можно было рассматривать как равноускоренное. Во всех экспериментах время t было одинаковым. Табл. 2 показывает рост скорости, а табл. 3 – ускорения микросфер с ростом параметра асимметрии a = x 0 /w .

Табл. 2. Экспериментально измеренные значения отношений величин скоростей движения полистироловых микросфер, захваченных с помощью асимметричных пучков ЛГ с одним и тем же топологическим зарядом n = 3, но с разными значениями параметра комплексного смещения x 0 /w = –iy 0 /w

x 0 / w = = – iy 0 / w		0	0,1	0,2	0,3	0,4	0,5
v v	x 0 x 0 = 0	1,0	1,2±0,2	1,3±0,2	1,4±0,2	1,8±0,3	1,9±0,3

Табл. 3. Экспериментально измеренные значения отношений величин ускорения полистироловых микросфер, захваченных с помощью асимметричных пучков ЛГ с одним и тем же топологическим зарядом n = 3, но с разными значениями параметра комплексного смещения x 0 /w=–iy 0 /w

x 0 / w = = – iy 0 / w	0	0,1	0,2	0,3	0,4	0,5
a x 0 a x 0 = 0	1,0	1,2±0,3	1,3±0,3	1,3±0,3	1,4±0,3	1,6±0,3

Показано, что нормированный ОУМ квадратично зависит от топологического заряда и параметра асимметрии пучка. Экспериментально показано, что скорости движения микрочастиц, захваченных в асимметричных пучках ЛГ, возрастают с ростом параметра симметрии при сохранении топологического заряда. Результаты расчёта (табл. 1) и эксперимента (табл. 2 и 3) согласуются.

Заметим, что интенсивность на световом полумесяце не постоянна (рис. 1 б , в и 2 б ), поэтому на частицу действует градиентная сила, которая приводит сначала к ускорению при движении до точки с максимальной интенсивностью и к замедлению после её прохождения. В силу симметрии интенсивности относительно центра полумесяца ускорение и замедление компенсируют друг друга, поэтому градиентная сила не учитывалась при анализе экспериментальных результатов.

Заключение

В данной работе получено выражение для плотности орбитального углового момента асимметричных лазерных пучков ЛГ. Показано, что нормированный ОУМ квадратично зависит от параметра асимметрии пучка, а плотность ОУМ – линейно. Экспериментально показано, что скорости движения микрочастиц, захваченных в асимметричных пучках ЛГ возрастают с ростом параметра симметрии при сохранении топологического заряда. Результаты расчёта (Таблица 1) и эксперимента (Таблицы 2 и 3) согласуются.

Работа выполнена при поддержке Министерства образования и науки РФ, гранта Президента РФ поддержки ведущих научных школ (НШ-9498.2016.9), а также грантов РФФИ 14-29-07133, 15-07-01174, 1537-20723, 15-47-02492, и 16-29-11698.