Передача сигналов инвариантным методом при наличии аддитивной стационарной гауссовской помехи с корреляционной функцией общего вида

В работах [1–5] инвариантная система передачи информации строилась таким образом, что на станции А (передающая сторона) информационные и обучающие части каждого передаваемого блока формировались отдельно.

Для этих случаев найдена вероятность ошибочного приема, которая, как минимум, на два порядка меньше вероятности ошибочного приема классических алгоритмов с амплитудной модуляцией.

В данной работе предлагается на станции А формировать информационные и обучающие сигналы, перемежающиеся между собой.

Постановка задачи . Имеем канал связи, ограниченный частотами f _н и f _в. Состояние канала связи определяется интервалом стационарности, внутри которого действие мультипликативной помехи описывается постоянством коэффициента передачи k ( t ) на определенной частоте.

Алгоритм приема определяется несущей частотой, задаваемой как средняя частота канала, и поднесущей, которой модулируется несущая.

Структуру блока определим для простоты как элементы информационной последовательности на четных местах в блоке, а обучающие сигналы, равные единице, на нечетных местах в блоке.

На приемной стороне результирующая произведения обучающих сигналов и опорного сигнала генератора усредняется и используется для демодуляции информационной части блока. При этом из-за изменения параметров канала связи информационные и обучающие сигналы зашумлены аддитивной помехой.

В данном исследовании предполагается, что отсчеты аддитивной помехи коррелированы между собой.

Необходимо произвести расчет вероятности попарного перехода инвариантов в такой системе. Для этого необходимо найти аналитическое выражение плотности вероятности оценки инварианта.

Решение поставленной задачи . Рассмотрим процесс передачи. На каждом шаге передается либо обучающий сигнал, амплитуда которого равна единице, либо информационный сигнал, принимающий значения 1, 2, 3, …, М , где М – объем алфавита инвариантной системы.

Информационный и обучающий сигналы передаются с защитным временным интервалом.

Это означает, что между соседними сигналами предусмотрена пассивная пауза (рис. 1). Совокупность информационных и обучающих сигналов сформирована в виде блоков. На рис . 1, к примеру, блок содержит семь элементов.

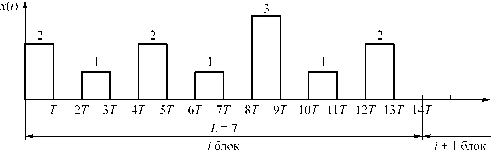
Рис. 1. Структура блока передаваемой информации

Длительность блока определяется как Т _бл = Т • 2 L , где Т – длительность сигнала; L – количество сигналов; x ( t ) – случайный процесс, принимающий значения, равные 1, 2, 3, …, M .

Сигнал передачи x ( t ) в дальнейшем модулирует поднесущую частоту, огибающая отсчетов которой подчиняется синусоидальному закону.

Информационный сигнал на приемной стороне имеет следующий вид:

Г _пр ( t ) = x ( t )• 5 ( t )• k + ^( t ) , где x ( t ) — сигнал передачи; 5 ⁽ t ) = A sin ( 2 n f _п t ) — поднесущая; k - коэффициент передачи канала; £ ( t ) - аддитивная помеха.

При приеме каждый сигнал в блоке считывается N раз через интервал времени A t и умножается на 5 ( t ).

Для каждого информационного сигнала I_i ( i = 1, …, M ) отсчеты берутся в моменты времени

t, „ =( 2l - 2) T + —T l,n                      N , где 1 < l < L, 1 < n < N; N- количество отсчетов.

Рассмотрим прием при наличии аддитивной и мультипликативной помехи.

Шум канала связи x( t ) является стационарным гауссовским случайным процессом с нулевым математическим ожиданием, дисперсией о ² и корреляционной функцией, подчиняющейся следующему закону [6]:

E (^( t )§( 0 )[о2 ) = R (t ) = E f^it+lMlI^,

V о ) где т - любое число в силу стационарности.

Оценка инварианта с учетом вышеописанных ограничений при воздействии мультипликативной и аддитивной помехи может быть вычислена следующим образом:

то

inv; =

E ( k - INV , - S ( t , n ) + ^ ( t , n ) ) - S ( t , n ) n = 1

N

# G ee ( ^- - ^s ( j м t„ )h ( . .. )

j^E n"           A

B где k – коэффициент передачи канала; INVl – l-й передаваемый инвариант; t(l n) – момент времени когда берется n-й отсчет в l-м сигнале; S(tln) - значение sin(2nfnt) в l-м сигнале на n-м отсчете; £(tln) - помеха в l-м сигнале на n-м отсчете; #(G) – число элементов множества G; G – множество номеров шагов, на которых передается обучающий сигнал.

При вычислении качественных характеристик, таких как вероятность попарного перехода необходимо знать выражение плотности распределения оценки инварианта.

Воспользуемся известным подходом оценки вероятности попарного перехода, описанным, к примеру, в [7]

Z р                    м

Р пер = P J W r ⁽ z ) dz + P 2 J W 1 ⁽ z ) dz •        (2)

0                     Zр где Pпер – вероятность перехода INV1 в INV2 и наоборот; Р1 – вероятность появления INV1; Р2 – вероятность появления INV2. Первый интеграл – вероятность появления INV2, когда послан INV1. Второй интеграл – вероятность появления INV1, когда послан INV2; Zр – пороговое значение, необходимое для вычисления Pпер; при известных Р1 и Р2 оно определяется с помощью наилучшей байесовской оценки путем минимизации Pпер по Zр. При неизвестных Р1 и Р2 выбираем Р1 = Р2 = 0,5.

На основании выражения (1) вычислим математические ожидания и дисперсии случайных величин А и В .

Математическое ожидание числителя будет равно [6] m A = E ⁽ A ) =

n=1

Математическое ожидание знаменателя будет равно [6] m B = E ⁽ B ) =

= 1 EE-'S2 (tj„)«     .

# (G )E E     (j •n)

Дисперсия числителя будет равна [6]

N cta = D(A ) = D |E* I • nS, • n| •(5)

V i=1

где ^ _ln = £ ( t , , n ) - отсчеты аддитивной помехи; S , _n = S ( t , , n ) -отсчеты информационного сигнала.

Тогда величину дисперсии числителя можно опреде-

лить через функцию ковариации [6]

NN aA = EEcov (^,, nS,, n; ^,, nS,, n) = n = 1 n - 1

NN

= EE ^S, • n^S, • n ^² corr ( ^ , • n ^ , , n ) '

n = 1 n ' = 1

Так как

t , • n ^- t ,

2 n - 1 T 2 N

2 n - 1

-

2 N

T = — ( n - n' ) T, N ^,

где R ( t ) = e

-(

я \ о f( n - n') T ) corr (^,• n ^,,n-)= R I      NI • alt - коэффициент корреляции; a - коэффи-

циент затухания, a экспериментально определен как a = 3 400.

Таким образом, с учетом вышесказанного дисперсия числителя будет равна

2 r;2 VV? T?^{f (} n ^- n ) T

^CT A = ^CT EE ^S,,n^S, , n^R I —77— n =1 n '=1               ^V N

.

то

Аналогично дисперсия знаменателя будет равна ст2 = D (B ) =---x

B             ( # ( G ) ) 2

NN xE E EE sj, nS, n-CT2 corr (^j, n ^-, n-).

j g G j 'e G n =1 n' =1

Так как

t - — j , n

t j- • n -= ( 2 j - 2 ) T +

+ 22 N T - ( 2 j' - 2 ) T -

2 n' - 1 T =

n - n '

N

2 N I T •

CTr =

B (#( G ))2 xEEE ES, nS, ,r ff 2 (j - j)+n jeG j'eG n = 1 n* = 1W

-

N

n ) T )    ⁽⁷⁾

Будем полагать, что функция корреляции числителя и знаменателя подчиняется следующему закону [6]:

p = corr ( A ; B ) =

cov ( A ; B )

^CT A ^ст B

где

cov ( A ; B ) =

NN

# ( G ) ^X

^x E E E ^S, , n^Sj, n ^CT corr ( ^ , , n ^jnn ) =

2 NN

CT

#I G)

EEE S , • A n R || 2 ( , - j ) +

n - n' 3 t ] N J J '

С учетом вышеприведенных выкладок выражение оценки инварианта запишем в следующем виде:

INV. = m A ^+ct A ⁽рП 1 + 4^{- -} p ² П 2 )

m B ^+CT b П 1

где n 1 и П ₂ являются независимыми случайными величинами, имеющими стандартное нормальное распределение.

Для описания плотности распределения W ( z ) оценки инварианта и удобства дальнейших вычислений положим П 1 = х .

m A +CT A ⁽p. x + 4 1 ^- p ² П 2 ) Тогда z =-------------------------,

m_B + ст _Bx

z ( m_B +ct B x ) = m A +ct A -p- x + ct a 4 1 -p ² n ₂,

П 2 =

z f m „ +ст„ x ) - m,

BBA

T|' 2 =

-

CT A 4 ^{1 -} p ² ( m B +C B x )

CT A .p. x

,

^CT A 4 ^{1 -} p ²

Аналитическое выражение плотности вероятности оценки инварианта будет равно

z(m_R + o_R x )- m. -o, -p- x )

BBAA

W(z) = j ф(x)ф

(

X

где Ф⁽ x ) = ,— e ^{x 2} .

2n

При расчете плотности вероятности оценки инварианта W ( z) величины o А и o В определяются выражениями (6) и (7), а величины m_A и m_B определяются выражениями (3) и (4).

Результаты машинного моделирования . Расчет Р _пер производился численно по выражению (2) аппроксимацией формулы (9).

В классических системах с амплитудной модуляцией аналогом вероятности попарного перехода является вероятность ошибки, которая рассчитывается по известным формулам [7].

Вероятность попарного перехода и вероятность ошибки вычисляются для одинаковых значений отношения сигнал/шум h , которое вычисляется по формуле [7]

N

2 k ² INV _l ² a h =----i—,

N о о где a = ^ S2 (i); о2 - дисперсия аддитивной помехи.

i = 1

Пороговые значения Z _р рассчитывались путем минимизации Р _пер в формуле (2). Для k = 1 и INV₁ = 1, INV₂ = 2; 3; 4; 5; 6 вычисления дают результаты Z _р = 1,307; 1,952; 2,438; 3,044; 3,55. Для k = 0,7 и INV₁ = 1, I^рNV₂ = 2; 3; 4; 5; 6 вычисления дают результат Z _р = 1,052; 1,853; 2,430; 2,916; 3,563.

Результаты моделирования приведены на рис. 2 и 3.

Передача амплитудно-модулированных сигналов, образованных INV _l и S _об, обеспечивает на основе классических алгоритмов обработки информации, как правило, невысокую помехоустойчивость [7]. И только после обработки этих сигналов в соответствии с алгоритмом частного по выражению (1), получаем оценку инварианта, по сути, являющуюся числом, а не сигналом.

Как видно из рис. 2 и 3 вероятность попарного перехода одного инварианта в другой при больших отношениях сигнал/шум определяется величинами (10–1...10–20). При пересчете указанных выше величин вероятность ошибочного приема единичного символа в классических системах лежит в пределах (10–2...10–5).

По сути дела, при таком способе модулирующий сигнал вкладывается в отношение энергии информационного сигнала к энергии обучающего сигнала.

Эта величина, как указано в [1–5] остается неизменной при работе по каналам с переменными параметрами и этим объясняется высокая помехоустойчивость сигналов приема.

В заключение отметим, что предложенная инвариантная система обладает высокой помехоустойчивостью по сравнению с обычными классическими системами: вероятность попарного перехода как минимум на два порядка меньше вероятности ошибки в классических системах. Это позволяет использовать предложенную систе- му в условиях повышенных требований к помехоустойчивости в телекоммуникационных системах и системах телеуправления.

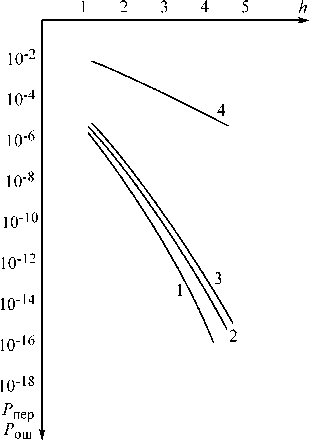
Рис. 2. Кривые помехоустойчивости инвариантной системы при отсутствии мультипликативной помехи: 1 – вероятно сть попарного перехода одного инварианта в другой при следующих заданных условиях: k = 1; INV₁ = 1; INV₂ = 2, 3, …, 6 и отсутствии корреляции; 2 – вероятность попарного перехода одного инварианта в другой при тех же условиях и наличии корреляции; 3 – вероятность попарного перехода одного инварианта в другой при тех же условиях и наличии слабой корреляции при R = 0,7; 4 – вероятность ошибки при классической амплитудной модуляции и когерентном приеме

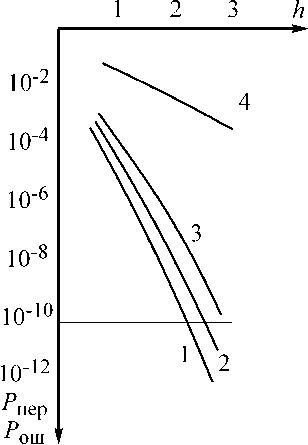
Рис. 3. Кривые помехоустойчивости при наличии мультипликативной помехи: 1 – вероятность попарного перехода одного инварианта в другой при следующих заданных условиях: k = 0,7; INV₁ = 1; INV₂ = 2, 3, …, 6 и отсутствии корреляции; 2 – вероятность попарного перехода одного инварианта в другой при тех же условиях и наличии корреляции; 3 – вероятность попарного перехода одного инварианта в другой при тех же условиях и наличии слабой корреляции при R = 0,7; 4 – вероятность ошибки при классической амплитудной модуляции и когерентном приеме

Предложенный способ формирования блока и его обработки улучшает качественные характеристики системы по сравнению со способом формирования информационной и обучающей последовательностей в виде отдельных частей блока.