Передача сигналов инвариантным методом с последующей нелинейной обработкой при наличии слабой корреляции

В работах [1–5] исследовались инвариантные системы передачи информации, которые имеют различные вероятности попарного перехода. Указанные инвариантные системы имеют существенно лучшие характеристики по сравнению с классическими системами амплитудной модуляции при комплексном воздействии помех.

Выигрыш в помехоустойчивости объясняется тем, что модулирующий параметр вложен в отношение энергий информационного и обучающего сигналов.

Однако следует отметить, что поиски построения подобных инвариантных систем не прекращаются. Данная работа посвящена дальнейшему исследованию характеристик инвариантной системы при использовании квадратичного детектирования, которое является нелинейной обработкой сигналов.

Постановка задачи. Имеется канал связи, ограниченный частотами f _н и f _в. Временную динамику каналов с переменными параметрами можно условно разбить на интервалы стационарности, а затем рассматривать прием информационного и обучающего сигналов в пределах выделенных интервалов стационарности, где действие мультипликативной помехи описывается постоянством коэффициента передачи k ( t ) на определенной частоте. Алгоритм приема определяется несущей частотой, задаваемой как средняя частота канала, амплитуда которой про-модулирована поднесущей.

Каждый передаваемый блок будет содержать информационную часть и последовательность обучающих сигналов S _об. При этом количество элементов информационной последовательности, отнесенное к количеству элементов обучающей последовательности, равно

N инф : N об 3:3

Из - за изменения параметров канала связи на инфор мационные и обучающие сигналы воздействует аддитив ная помеха .

Решение поставленной задачи. На приемной сторо не обучающие сигналы усредняются и используются для демодуляции информационной части блока и для умень шения влияния аддитивных шумов канала связи .

Структура приемной части инвариантной относитель ной амплитудной модуляции ( рис . 1) содержит синхронный детектор ( умножитель , ФАПЧ и ФНЧ ) и спецвычислитель .

В силу того, что мультипликативная помеха одинаково воздействует на обе части каждого передаваемого блока, алгоритм демодуляции сигналов приема, с учетом выбранного способа обработки сигналов, будет заключаться в вычислении оценки инварианта.

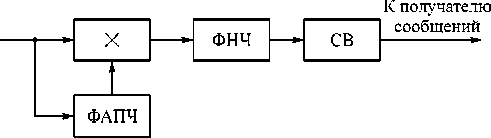
Рис . 1. Структурная схема инвариантной системы передачи информации : ФАПЧ – устройство фазовой автоподстройки частоты ; ФНЧ – фильтр нижних частот ;

СВ – спецвычислитель

Поскольку используется нелинейный квадратичный алгоритм в вычислении оценки инварианта , то справед ливо следующее соотношение :

£ ( к ■ INV i ■ 5 ( i ) + ^( i ) ) 2

^INV * 2 = 1      ------------------------------ ⁵об . (1)

7 ££ ( k ■ ⁵ об ■ ^{5 (} j ⁾⁺n⁽ m , j ))

L m =1 j =1

В числителе выражения (1) представлена сумма N квадратов мгновенных отсчетов сигнала информационной посылки. Информационный сигнал образован поднесущей вида

5(i ) = A sin (2nfп ■At ■ i), где A - амплитуда;/ - частота колебаний поднесущей; At -интервал дискретизации и представляет собой выражение

C (i ) = к ■ INVl ■ 5 (i )+^( i), где к ■ INVl ■ 5 (i) - мгновенный отсчет сигнала информационной части блока, поступающего из канала; ^(i) -отсчеты аддитивной помехи, распределенные по нормальному закону; k – коэффициент передачи канала связи на интервале стационарности.

В знаменателе выражения (1) представлена сумма N квадратов мгновенных отсчетов сигнала обучающей посылки, образованного поднесущей

G(m ) = к ■ 5об ■ 5(i ) + n( m, j), где n(m, j) - помеха в m-й реализации обучающего сигнала, распределенная по нормальному закону; к■ 5об5(i) -мгновенный отсчет сигнала обучающей части блока, поступающего из канала; L – количество накоплений G(m).

Без ограничения общности полагаем, что S _об = 1. Если 5 об ^ 1, то все исходные параметры, а именно INV l и о ^ (среднеквадратическое отклонение помехи ^ ( i ), n ( m , j )) можно масштабировать на величину S _об.

Тогда формула (1) с учетом введенных ограничений перепишется в виде

N

£ ( k ■ INV i ■ 5 ( i ) + ^( i ) )

I^NV * 2 =       --------------------_Г = B ,   (2)

7 ££^{( k} ■ ^{5 (} j ⁾⁺n⁽ m , j ))

L m =1 j =1

где переменные описаны выше.

Будем полагать, что случайные величины ^(i) и n(m, j) одинаково распределены по нормальному закону с нулевым математическим ожиданием и дисперсией сЛ Кроме того, предполагается, что в каждом блоке зависимы только соседние случайные величины. Тогда corr(^(i), ^(i-1 )) =

= corr(n( m, j), n(m, j-1 )) = R, где R – коэффициент корреляции.

Все остальные случайные величины, входящие в каждый принимаемый блок, будут независимыми. Для реализации этой модели необходимо, чтобы I R I <  1/42 .

Воспользуемся известным подходом оценки вероятности попарного перехода, описанным формулой средней вероятности [6]

z р ²

от

P™ _Р= P f Wi ( z ) dz + P I" W ( z ) dz , пер    ii

^z р ²

где P _пер – вероятность перехода INV ₁ ² в INV _i ² и наоборот; Р ₁ – вероятность появления INV ₁ ² ; Р_i – вероятность появления INV _i ² ; первый интеграл – вероятность появления INV _i ² , когда послан INV ₁ ² ; второй интеграл – вероятность появления INV ₁ ² , когда послан INV _i ² ; z _p ² – пороговое значение, необходимое для вычисления P _пер; при известных Р ₁ и Р_i оно определяется с помощью наилучшей байесовской оценки путем минимизации P _пер по z _p ² .

При неизвестных Р ₁ и Р_i выбираем Р ₁ = Р_i = 0,5.

Из анализа (3) видно, что для вычисления Pпер необходимо знать аналитические выражения W1(z) и Wi(z) плот- ности вероятности оценки инварианта.

При нелинейной обработке и вычислении величин инвариантов появляется смещение. Это смещение обусловлено тем, что в формуле (3) величины W ₁( z ), W_i ( z ) вычисляются для квадратов инвариантов. Пороговое значение z _р в выражении (3) также возведено в квадрат. Смещенные квадраты инвариантов в формуле (3) обозначены INV ₁ ² и INV _i ² .

На основании выражения (2) вычислим математические ожидания и дисперсии случайных величин А и В . Математическое ожидание числителя будет определяться формулой [7]:

N mB = £(k2 INVl2 5(i)2 + с2).         (4)

i =1

Математическое ожидание знаменателя определится по формуле [7]

N mB = £( k2 5(i )2+g 2).             (5)

i =1

Дисперсия числителя определится как [7] N

D B = 4 k ² INV l ² с ² £ 5 ² ( i ) + 2 N с ⁴ + i =1

N -1

+ 8 £ k ² INV l ² 5 ( i ) 5 ( i + 1) с ² R + 4( N - 1) R 2 с ² .   (6)

i =1

Дисперсия знаменателя определится по формуле [7]

N

D = 1(4 k 2c2^ 52 (i) + 8 k 2с2 R x L ы x£ 5 (i) 5 (i + 1) + 2 N с4 + 4 (N-1) R2 с4).    (7)

i =1

Расчет частного двух случайных величин производится по формуле [7]

„        ₁         - ( zx ^{- m} B ) ² - ( x ^{- m} B ) ²

W ( z )= [---------- e    ^2с B e   ^{2с B} \x\Xx , (8)

J„ 2пс B с B где с А и с В определяются выражениями (6) и (7); mB и mB определяются выражениями (4) и (5).

Следует отметить, что в формуле (3) при расчете W ₁( z ) используется INV₁, а при расчете W_i ( z ) – INV _i . Значение вероятности попарного перехода P _пер находилось методом численного интегрирования. Число накоплений с усреднениями равно 40.

Полученные данные ограничены первыми шестью парами сравниваемых инвариантов, когда INV₁ = 1, INV _i = 2; 3; 4; 5; 6; 7.

Вероятность попарного перехода вычислялась при значениях h – отношения сигнал/шум, которое находилось по формуле, определяемой отношением мощности сигнала к мощности шума

2 k ² INV l ² a h =----i—

N с 2

.

Пороговые значения z ² отыскивались минимизацией P _пер в формуле (3). Для k = 1 ^p , R = 0,7 и INV₁ = 1; INV _i = 2; 3; 4; 5; 6; 7 вычисления дают z _p ² = 1,521; 2,047; 2,513; 3,406; 4,117; 4,595. Для k = 0,7, R = 0, ^p 7 и INV₁ = 1; INV _i = 2; 3; 4; 5; 6; 7 вычисления дают z _p ² = 1,341; 1,689; 2,117; 2,617; 2,970; 3,401.

Особенностью любой инвариантной системы, основанной на принципе инвариантной относительной амплитудной модуляции, является то, что по каналу передаются амп-литудно-модулированные сигналы, образованные INV _l и S _об.

Передача этих сигналов обеспечивается на основе классических алгоритмов обработки информации и имеет невысокую помехоустойчивость, и только после обработки этих сигналов в соответствии с алгоритмом частного по выражению (2), получаем оценку инварианта, по сути являющуюся числом, а не сигналом.

Кривая 2 (рис. 2, 3) соответствует вероятности ошибки Р _ош в классических системах, являющейся аналогом вероятности попарного перехода и рассчитывающейся по известным формулам [6].

Таким образом, вероятность попарного перехода в инв ариантной системе определяется в еличинами (10 ^–1 …10 ^–18 ). При тех же значениях сигнал/шум вероятность ошибочного приема единичного символа в классических системах лежит в пределах (10 ^–1 …10 ^–5 ).

Проведенный анализ показывает, что инвариантная система передачи информации при наличии аддитивной помехи с некоррелированными отсчетами обладает высокой помехоустойчивостью. Вероятность ошибки классического алгоритма с амплитудной модуляцией как минимум на два порядка больше вероятности попарного перехода в инвариантной системе.

Хотелось бы подчеркнуть, что система с квадратичной нелинейной обработкой существенно проще в реализации по сравнению с инвариантными системами, разработанными авторами ранее [1–5]. Упрощение состоит в том, что в разработанном выше алгоритме не требуется расширенного синхронного детектирования, поэтому данную систему можно использовать в телекоммуникационных системах, системах телеуправления и других системах, предъявляющих высокие требования к помехоустойчивости.

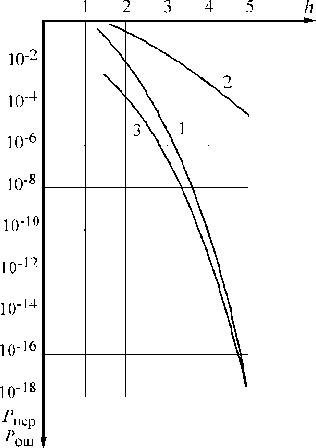
Рис. 2. Помехоустойчивость инвариантной системы при отсутствии мультипликативной помехи и INV1 = 1;

INV _i = 2; 3; 4; 5; 6; 7: кривая 1 – вероятность попарного перехода при слабой коррелированности отсчетов шума и нелинейной обработке отсчетов сигнала;

кривая 2 – вероятность ошибки классической АМ;

кривая 3 – вероятность попарного перехода при некоррелированности отсчетов шума и использовании расширенного синхронного детектора