Передача спинового углового момента диэлектрической микрочастице

В недавних работах авторов были теоретически обнаружены новые оптические эффекты в остром фокусе лазерного света с фазовой и поляризационной сингулярностями. Было обнаружено формирование обратного потока энергии вблизи фокуса на оптической оси [1] и тороидального потока энергии вокруг «тёмных колец» в плоскости фокуса, на которых поток энергии нулевой [2]. Был обнаружен эффект «углового трактора», когда на соседних световых кольцах в плоскости фокуса поперечный поток энергии направлен в разные стороны (по часовой и против часовой стрелки) [3]. Также было строго теоретически показано, что при острой фокусировке Гауссова пучка с круговой поляризацией в остром фокусе возникает спиральный поток энергии из-за спин-орбитальной конверсии [4]. Спин-орбитальная конверсия и связанные с ней оптический эффект Холла и вращение микрочастиц по круговой траектории исследовались также в работах [5–8]. В последние годы в области острого фокуса лазерных вихревых пучков и пучков с неоднородной поляризацией обнаружен ряд других новых и интересных эффектов: формирование клубков и узлов из точек фазовой и поляризационной сингулярностей [9–11], фотонные колеса [12], формирование поляризационных полосок Мёбиуса [13, 14], полная магнетизация [15, 16]. Все эти эффекты продемонстрированы численно, а неко- торые экспериментально, но нет строгой аналитической теории для их описания.

В данной работе на основе теории Ричардса– Вольфа [17], с помощью которой адекватно описываются все 6 проекций электрического и магнитного векторов электромагнитного поля вблизи фокуса, дано строгое описание некоторых из перечисленных выше интересных эффектов. Также экспериментально продемонстрирована предсказанная в [4] спин-орбитальная конверсия, которая приводит к формированию орбитального углового момента в остром фокусе простого Гауссова пучка с круговой поляризацией. Этот орбитальный угловой момент передаётся захваченной в фокусе микрочастице и вращает её вокруг оптической оси (и вокруг своего центра масс). Ранее в [6, 8] также вращали диэлектрическую микрочастицу в Гауссовом пучке, но по круговой траектории, а не вокруг своего центра масс.

Спин-орбитальная конверсия в фокусе

Пусть начальное поле – это оптический вихрь с топологическим зарядом n , произвольной осесимметричной радиальной частью и круговой поляризацией:

(1 )            ™ Г^- i с)

E = A ( 9 ) e™ ^ф      , H = A ( 9 ) e ™ ^ф        ,         (1)

Ii g)                  ( 1 J где с = 1 для правой круговой поляризации, с = -1 для левой круговой поляризации, с = 0 для линейной по- ляризации, и а Ф 0,±1 для эллиптической поляризации (ниже предполагается, что а - действительное число). Плотность спина электрического поля (без учёта спина магнитного поля) рассчитывается по известной формуле [18] (спиновый угловой момент)

чай, для левой круговой поляризации ( с =-1, Y ₊ = 0, Y - = 1) получим:

s E

16 п w

Im ( E * x E ) ,

S ex - = Q ( r )sin ф ,

S Ey - = - Q ( r )cos ф , 22

^sEz -     I 2, m -2    I 0, m ,

Q ( r ) = 1 1, m -1 ( 1 0, m + 1 2, m -2 ) .

где w – циклическая частота света, Im – мнимая часть числа. В дальнейшем постоянную (1/8 п w ) будем опускать, E и H в (1) и (2) – это вектора напряжённостей электрического и магнитного поля электромагнитной волны. Тогда, согласно формализму Ричардса–Вольфа [17], в плоскости фокуса получим проекции вектора плотности спина (2) в виде:

Из (6) видно, что для оптического вихря с левой круговой поляризацией в фокусе присутствуют все компоненты вектора плотности спина. Если вместо оптического вихря взять Гауссов пучок ( m =0) с левой круговой поляризацией, то в плоскости фокуса по-прежнему будут отличными от нуля все компоненты спина:

S ex = sin ф ( -СУ₊ 1 0, m l 1, m +1 - CY - 1 0, _тТ 1, m -1 —

• ^{-    Y} + ¹ 1, m +1 ¹ 2, m+ 2 ⁺ У ^{2 1} 1, m -1 ¹ 2, m -2 ) ⁺

• +    Sin 3 фY + Y - ( 1 1, m -1 1 2, m+ 2 - 1 1,m +1 1 2, m -2 ) , S Ey = COS ф ( У + 1 0, m l 1, m +1 -Y - 1 0, m l 1, m -1 +

• ^{+    Y} + ¹ 1, m +1 ¹ 2, m +2    У - ¹ 1, m -1 ¹ 2, m -2 )

• -    COs3 фY + Y - ( 1 1, m -1 1 2, m +2 - 1 1, m +1 1 2, m -2 ) , s Ez = ^{С 1} 02, m -^Y + ¹ 2, m +2 ⁺ Y - ¹ 2^ m -2 ⁺

• +    COs2 фY + Y - 1 0, m ( 1 2, m -2 - 1 2, m + 2 ) •

S ex 0- =- Q ( r )sin ф ,

SEy0- = Q (r)cos ф, sEz 0- = 1 2,2 1 0,0,

В (3) используются обозначения интегралов:

1 _{0 v} =| ^ f | J sin 0 cos ^1/2 0 (1 + cos 9 ) x

V X Y 0

x A ( 9 ) e ik ^{cos 9} J _v ( x )d 9 ,

1 1, _v = [ ^ f | j sin ² 9 cos ¹/² 9 A ( 9 ) x

V X Y 0

x e ik ^{cos 9} j _v ( x )d 9 ,

1 ₂, _v = f f ) j sin 9 cos ¹/² 9 (1 - cos 9 ) x

V X Y 0

x A ( 9 ) e^{i ik cos 9} J _v ( x )d 9 ,

где f – фокусное расстояние апланатической системы, X - длина волны, NA = sin a - числовая апертура, J v ( x ) - функция Бесселя первого рода, x = kr sin 9 , ( x , y , z ) и ( r , ф , z ) - декартовы и цилиндрические координаты. В качестве амплитуды входной функции A ( 9 ) можно использовать функцию Бесселя–Гаусса [19]:

A(9) = J1 [ 2p -in9 | exp V   sin a J

( sin 9

V sin a

где P - отношение радиуса значка апланатической системы к радиусу перетяжки Гауссова пучка, а также где Y ₊ = (1 ±с )/2, и при с = 0 выбираются другие константы y+ = Y- = 1/ 72 . Из (3), как частный слу

^{Q (} r ) = 1 1,1 ( I 0,0 ⁺ I 2,2 ) .

Из-за оптического эффекта спин-орбитальной конверсии в фокусе для Гауссова пучка с левой круговой поляризацией будет отличным от нуля поток энергии [4]. Действительно, для проекций вектора Пойнтинга (потока энергии) [17]:

S = — Re Г е x H * 1 , 8 n ^{L J}

где c – скорость света в вакууме, Re – действительная часть числа, E × H – векторное произведение, * – комплексное сопряжение (далее постоянную c /(8π) опустим), получим в плоскости фокуса для оптического вихря с однородной поляризацией:

_ Г 1 + С ²

^Sz =1 T

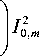
22    22

^Y + ¹ 2, m +2     Г - ¹ 2, m -2 ,

S x =- Q ( r )sin ф ,

S y = Q ( r )cos ф ,

Q ( r ) = Y + 1 1, m +1 ( 1 0, m + 1 2, m +2 ) +

^{+ Y} - ¹ 1, m -1 ( ¹ 0, m ^{+ 1} 2, m -2 ) .

Из (9) и (10) для Гауссова пучка с левой круговой поляризацией следует:

S z 0- = ¹ 0,0 ¹ 2,2 ,

S x 0- = Q ( r )sin ф ,

S y 0- =- Q ( r )cos ф ,

^{Q (} r ) = 1 1,1 ( I 0,0 ⁺ I 2,2 ) .

Сравнивая (7) и (11), видим, что в фокусе, кроме распределения вектора плотности спина (7), присутствует такой же по величине поток энергии (11). Они равны с точностью до знака, то есть поперечный поток энергии вращается ( S _{Ф -}= Q ( r ), S_{r -}=0) в противопо-

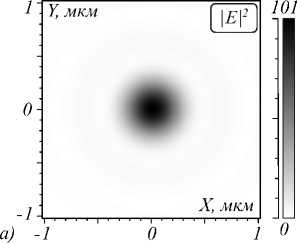
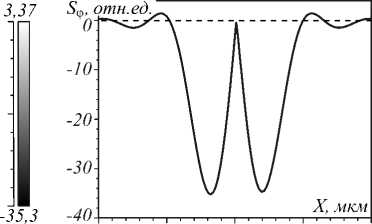
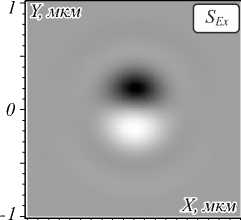
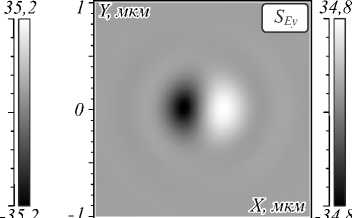
ложную сторону (по часовой стрелке) по отношению к направлению векторов плотности спина (они направлены против часовой стрелки). На рис. 1 показаны распределение интенсивности в фокусе (а) плоской волны с левой круговой поляризацией (вращение векторов поляризации против часовой стрелки), а также распределение в фокусе азимутальной составляющей Sϕ поперечного потока энергии (б) и его радиальное сечение (в). Также на рис. 1 показаны проекции вектора плотности спина в плоскости фокуса: sEx (г), sEy (д) и sEz (е). Положительные значения Sϕ на рис. 1б, в показывают вращение вектора Пойн-тинга S в плоскости XY по часовой стрелке, отрица- тельные – против. Из рис. 1г, д видно, что поперечные проекции векторов спина направлены против часовой стрелки. Из сравнения рис. 1б и рис. 1в, г видно, что поперечный поток энергии и поперечное распределение векторов спина равны по величине и противоположны по знаку. Это также видно из сравнения формул (7) и (11). Результаты на рис. 1 были получены при расчёте FDTD-методом с параметрами: длина волны λ =532 нм, сетка отсчётов с шагом λ/30, плоская волна на входе ограничена апертурой диаметром 8 мкм, фокусное расстояние f =4,55 мкм (числовая апертура NA = 0,65).

/        в) -1

г)-Т                        ;

б) -1

д) -1 о 1

Рис. 1. Интенсивность электрической компоненты |E|² (а) (негатив), азимутальная проекция вектора Пойнтинга S φ

(негатив, радиальная равна нулю) (б) и её сечение вдоль оси X через оптическую ось (в), а также проекции вектора плотности спина в плоскости фокуса: s Ex (г), s Ey (д) и s Ez (е) (негатив)

На рис. 2 показаны распределения поперечных проекций вектора плотности спина s Ex (а), s Ey (б) на расстоянии 500 нм от плоскости фокуса. Видно, что вектора спина повернулись на некоторый угол по часовой стрелке. Проведённое моделирование показало, что поперечный поток вектора спина вращается в том же направлении, что и поперечный поток энергии (рис. 1 б,в ). Так как у Гауссова пучка нет вихревой фазы (орбитальный угловой момент равен нулю), то поперечный поток энергии в плоскости фокуса порождается поперечным потоком спина. Поэтому и вращаться они должны в одном направлении. В заключительном параграфе мы покажем экспериментально, что этот поперечный поток энергии (орбитальный угловой момент) частично можно передать микрочастице, чтобы она вращалась относительно центра масс.

Из (10) следует, что если на входе у Гауссова пучка поменять круговую поляризацию с левой на правую, то поперечный поток энергии сменит направление движения и будет вращаться против часовой

стрелки. Моделирование показывает, что и поперечный поток спина вблизи фокуса также изменит свое направление и будет вращаться против часовой стрелки. В эксперименте это подтверждается вращением микрочастицы также против часовой стрелки.

В заключении этого параграфа покажем, что поперечный поток спина меняет знак при смене направления вращения круговой поляризации. Действительно, поток вектора спина связан с вектором плотности спина s E соотношением [20]:

S sp

= ∇× Im E ^* × E =∇× s .

2 k                      ^E

Из (12) для поперечной азимутальной проекции

вектора потока спина можно получить:

sp ϕ

∂ s Er _- ∂ s Ez k ∂ z k ∂ r ^.

а)

[ LHCP z=f+2X ]

Рис. 2. Распределения поперечных проекций вектора плотности спина sex (а), sEy (б) на расстоянии 2Л за плоскостью фокуса при фокусировке Гауссова пучка с левой круговой поляризацией. На рис. 1 эти же величины показаны в плоскости фокуса: sEx (г), sEy (д)

б)

Для случая круговой поляризации в фокусе радиальная составляющая вектора плотности спина равна нулю, так как из (6) следует:

s_Er = s_Ex cos ф + s_Ey sin ф = 0.

Поэтому для случая круговой поляризации и Гауссова пучка ( m =0) азимутальная проекция вектора потока спина в фокусе будет равна:

S = д S ez ^{sp ф}      k d r

.

Из (7) и (15) следует, что поперечный поток спина для левой поляризации S_sp ф _0-< 0 направлен по часовой стрелке, а для правой круговой S_sp ф ₀₊ > 0 - против часовой стрелки:

¹ sp ф0-

^{д S}Ez 0 k д r

, - ( I 0,0    I 2,2 ) =   S sp ф0+ ,

k д r

где

S sp ф0- =- 2 X

a

I_{2 2} — jsin ² 9 cos ¹/² 9 (1 1 2 X 0

- cos 9 ) A ( 9 ) x

X

x ( J ₁ ( x ) - J ₃ ( x ) ) d 9 ) +

0 I      [ sin ² 9 cos ¹/² 9 (1 + cos 9 ) A ( 9 ) x

’ ( X 0₆

X J1(x)d9)

< 0.

Неравенство (17) верно вблизи оптической оси ( kr < y , у - первый корень функции Бесселя J ₁( x )).

Орбитально-спиновая конверсия в фокусе и лента Мёбиуса

Поток энергии в световом поле можно представить в виде суммы орбитального потока энергии и потока спина [20]. Поэтому, наряду со спин-орбитальной конверсией, должен существовать и обратный эффект – орбитально-спиновая конверсия. Действительно, полагая в (3) с = 0 (линейная поляризация), получим выражения для осевой проекции вектора плотности спина в фокусе для оптического вихря с линейной поляризацией, направленной вдоль оси X :

s Ez

= 2 ( ¹ 2, m +2

⁺ I 22, m -2 ⁺

+ cos 2 ф 1 0, m ( 1 2, m -2 - 1 2, m +2 ) ) .

Из (18) следует, что при m =0 (Гауссов пучок) осевая проекция спина (18) равна нулю, а уже при m = 1 она отлична от нуля:

^sEz 1 = 2 ( I 2,1 ⁺ I 2,3 ) ( I 2,1 ^- I 2,3 ^- cos ^{2 ф} I 0,1 ) . ⁽¹⁹⁾

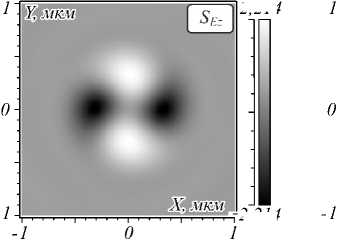
Из (19) видно, что имеет место эффект орбитально-спиновой конверсии. Действительно, оптический вихрь с линейной поляризацией на входе в оптическую апланатическую систему имеет вектор плотности спина, равный нулю, но имеет отличный от нуля поперечный поток энергии из-за спиральной фазы. А в плоскости фокуса вектор плотности спина отличен от нуля и имеет осевую проекцию (19). Хотя на самой оси ( r =0) продольная составляющая спина (19) равна нулю. Заметим, что в данном случае (на входе оптический вихрь с линейной поляризацией, m = 1) в фокусе у вектора плотности спина (2) есть и поперечные составляющие, которые можно получить из общего выражения (3). Из (19) видно, что при ф~ 0 (вблизи горизонтальной оси X ) первый сомножитель положительный, а второй отрицательный (так как I 0,1 >  I 2,1 ), и поэтому s_{Ez 1}< 0. А при ф»п /2 (вблизи вертикальной оси Y ) первый сомножитель в (19) по-прежнему положительный и второй сомножитель положительный (так как I 0,1 + I 2,1 >  I 2,3 ), и поэтому s Ez 1 >0. Это верно вблизи оптической оси ( kr <  y , Y — первый корень функции Бесселя J 1 ( x )). Выводы на основе формулы (19) подтверждаются моделированием. На рис. 3 показаны рассчитанные FDTD-методом осевая проекция спина s Ez (а) и интенсивность | E |² в фокусе для случая оптического вихря ( m = 1) c линейной поляризацией. Остальные параметры такие же, как для рис. 1.

Из рис. 3 а видно, что продольная составляющая вектора спина вдоль вертикальной оси ( Y -оси) направлена по направлению оптической оси, а спин вдоль горизонтальной оси ( X -оси) направлен в обратном направлении. Это означает, что в плоскости фо-

куса вектора поляризации вращаются в разных направлениях вблизи вертикальной и горизонтальной осей: вблизи X -оси – по часовой стрелке, а вблизи Y -оси – против часовой.

Из рис. 3 в видно, что вектор спина в каждой точке в плоскости фокуса на окружности радиуса 3,5 мкм (эта окружность проходит через четыре максимума в распределении вектора спина) описывает полоску Мёбиуса.

В фокусе, кроме продольной составляющей спина (19), очевидно, есть продольный и поперечный потоки энергии:

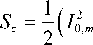
I 2, m +2    I 2, m -2

S = - Q ( r )sin ф ,

S y = Q ( r )cos ф ,

Q ⁽ r ) = 2 ¹ 1, m +1 ( ¹ 0, m ^{+ 1} 2, m +2 ) ⁺

⁺ 2 1 1, m -1 ( I 0, m ⁺ I 2, m -2 ) .

Из (20) видно, что в отличие от осевой составляющей спина (18), осевая проекция вектора Пойнтинга имеет круговую симметрию, как и распределение интенсивности (рис. 3 б ).

2,214

а)

-1

2,214

б)

Рис. 3. Распределение продольной компоненты плотности спина s Ez (а) и интенсивности |E|² (б) (негатив) в плоскости фокуса. Также показана лента Мебиуса, состоящая из векторов спина, в плоскости фокуса

в)

на окружности радиуса 0,35 мкм на фоне распределения s Ez (в)

Фотонные колёса или фотонный вертолёт

В предыдущем параграфе было показано, что в случае фокусировки Гауссова пучка с линейной поляризацией в плоскости фокуса продольная составляющая вектора плотности спина равна нулю. Но оказывается, что поперечные составляющие вектора плотности спина в фокусе в этом случае отличны от нуля. Действительно, из (3) для линейной поляризации ( c = 0, y₊ = у - = 1/ V2) получим при любом m :

s Ex = 2 sin ^ф ( 1 1’ m +1 1 2, m ⁺ 2 ^{+ 1} 1, m "* ¹ 2, m "² ) ⁺

• ⁺    2 ^sin 3 ф ( I 1, m -1 1 2, m +2 ^{- 1} 1, m +1 ¹ 2, m -2 ) ’

S Ey = 2^C0S ф ( V² 1 o, m l 1, m +1 ^- V² 1 0, m l 1, m -1 ^{+           (21)}

• ^{+    1} 1, m +1 ¹ 2, m +2 ¹ 1, m -1 ¹ 2, m -2 ) - 2 cos 3 ф ( 1 1, m -1 1 2, m +2 - 1 1, m +1 1 2, m -2 ) ’

и при m =0 ( s Ez 0 =0):

S Ex 0 =- 2cos Ф sin2 ф 1 1,1 1 2,2 ,                       (22)

s_Ey 0 = 2cos ф cos2 ф 1 1,1 1 ₂,₂ + V2cos ф 1 0,0 1 1,1 .

Из (22) видно, что на самой оптической оси поперечного вектора спина нет, также нет спина вдоль вертикальной оси (ф = ±п/2). Вектор спина (22) справа (при -п/2< ф < п/2) от вертикальной оси Y направ- лен вдоль положительного направления вертикальной оси Y. При ф = 0 из (22) следует, что

• ^S Ey = V² 1 1,1 ( V2 I 2,2 ⁺ 1 0,0 ) >  0 .

Слева от вертикальной оси (при п /2< ф <3 п /2) поперечный спин направлен вдоль отрицательного направления оси Y. При ф = п из (22) следует, что

S Ey =- V2 1 1,1 ( V2 1 2,2 + 1 0,0 ) < 0.

Так как вектор спина в каждой точке перпендикулярен к эллипсу (или кругу) вращения вектора поляризации, то получается из (22), что слева и справа от оптической оси вектора поляризации вращаются в горизонтальной плоскости в разных направлениях (как винты у вертолёта). Этот эффект аналогичен эффекту фотонных колёс [12], но так как плоскость вращения вектора поляризации не вертикальная, а горизонтальная, то напрашивается аналогия с вращением винтов у вертолёта. Для того, чтобы плоскость вращения вектора поляризации вблизи фокуса была вертикальная (фотонные колёса), надо, чтобы освещающий пучок имел не горизонтальную, а вертикальную поляризацию.

На рис. 4 показаны распределения поперечных проекций вектора плотности спина (спинового углового момента) в фокусе Гауссова пучка с линейной поляризацией (вектор поляризации направлен вдоль оси X ). Остальные параметры такие же, как на рис. 1.

Видно, что величина Y -й компоненты s Ey более, чем в 30 раз больше, чем величина X -й компоненты s Ex вектора спина. Поэтому компонентой s Ex можно пренебречь. А из вида и знака s Ey на рис. 4 а можно сделать вывод, предсказанный теорией (21), что в плоскости фокуса слева и справа от плоскости YZ вектор спина

а)

б)

направлен вертикально и в разные стороны. Это показывает, что в плоскости XZ лежат эллипсы поляризации (или круги), по которым вращается во времени вектор напряжённости электрического поля. Такая конфигурация эллипсов поляризации напоминает вращение винтов вертолёта (рис. 4 в ).

Рис. 4. Распределение в плоскости фокуса поперечных проекций (продольная равна нулю) вектора плотности спина:

s Ey (а) и s Ex (б). Иллюстрация аналогии с вращением винтов вертолёта (в)

Только продольная компонента спина в фокусе (полная магнетизация)

Если фокусировать оптический вихрь с топологическим зарядом m и азимутальной поляризацией, то амплитуда для такого поля запишется в виде (вместо (1)):

- sin ф^ E = A ( 9 ) e im ^ф 1       ч,

(cos ф )

cos ф н = a ( 9 ) e im ^ф 1      ч.

( sin ф J

Тогда в плоскости фокуса получим выражение для продольной компоненты вектора плотности спина:

s Ez

I 0, m -1 + I 2, m -1

1² - V .

^Г0, m +1 ⁺ I 2, m +1 I ) .

Из (24) следует, что так как в плоскости фокуса только одна продольная компонента вектора плотности спина отлична от нуля, то имеет место эффект полной магнетизации [14]. Так как поперечные компоненты вектора спина для любого m равны нулю ( 5 ф = S r =0), то плоскость, в которой вращаются все вектора поляризации, совпадает с плоскостью фокуса.

В [21] получено выражение в фокусе для продольной компоненты вектора Пойнтинга для оптического вихря с топологическим зарядом m и азимутальной поляризацией n -го порядка

z 2 ( ² 0, m + n

22  2

⁺ 0, m - n 2 m, m + n -2   -*2, m - n +2

из которого следует, что поток энергии вдоль оптической оси для оптического вихря с азимутальной поляризацией ( n = 1) описывается выражением:

I 0, m +1 ⁺ I 0, m -1    I 2, m -1    I 2, m +1

На рис. 5 рассчитанные по формулам (24) и (25) продольные компоненты в плоскости фокуса для распределения вектора потока энергии (а) и вектора плотности спина (б). Параметры расчёта: длина волны X = 532 нм, фокусное расстояние f = 100 X , порядок вихря (топологический заряд) m = 1, числовая апертура NA = sin 9 = sin 85° = 0,996, расчётная область -3 X <  x , y < 3 X .

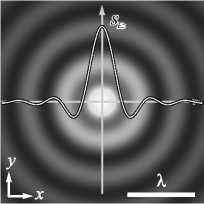
Рис. 5. Распределение продольной составляющей вектора Пойнтинга S z (чёрный цвет – ноль, светлый цвет – максимум) (a) и продольной составляющей вектора

б)

плотности спинового углового момента s E,z (чёрный цвет – минимум, светлый цвет – максимум) (б) остросфокусированного оптического вихря (m=1), прошедшего узкую кольцевую диафрагму, в фокальной плоскости. График на рисунке (a) – сечение s E,z

Из рис. 5 видно, что продольная компонента спина меняет знак от кольца к кольцу потока энергии. Это означает, что на разных радиусах картины потока энергии в фокусе направление вращения векторов поляризации разное. На оптической оси поток энергии и плотность спина максимальные (рис. 5) и равны соответственно: S_z 1 = (1/2)( 1 ₀²,₀ - 1 2,₀ ) > 0 и s_Ez 1 = (1/4)1 1 о,о + 1 ₂,₀ | 2 . Это видно из (24) и (26) при m =1 и r =0.

Эксперимент по демонстрации спин-орбитальной конверсии в фокусе

Оптическая схема эксперимента показана на рис. 6. Исходный линейно-поляризованный лазерный пучок с Гауссовым профилем распределения интен-

сивности, излучаемый твердотельным лазером (λ =532 нм, P output = 100 мВт), с помощью четвертьволновой пластинки QP преобразовывался в пучок с круговой поляризацией. С помощью системы зеркал M1, M2 и M3 лазерный пучок направлялся во входное отверстие микрообъектива MO1 (40×, NA=0,65) и фокусировался им внутри ячейки C, образованной двумя покровными стёклами и содержащей водный раствор с полистироловыми частицами. Микрообъектив MO2 (40×, NA=0,65) строил изображение плоскости манипулирования на матрице видеокамеры CAM (TOUP-CAMUCMOS08000KPB, размер пикселя – 1,67 мкм). Система из осветительной лампы I, линзы L с фокусным расстоянием 150 мм и полупрозрачного зеркала M4 была использована для подсветки раствора частиц. Результаты экспериментов по вращению частицы полистирола, которая имела форму вытянутого сфероида с размерами осей примерно 2×1 мкм, с помощью Гауссова пучка с левой или правой круговой поляризацией показаны на рис. 7 и 8.

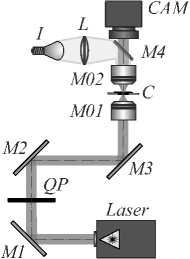
Рис. 6. Оптическая схема эксперимента по исследованию вращения частиц в Гауссовом пучке с круговой поляризацией: Laser – твердотельный лазер (λ=532 нм, P output =100 мВт), QP – четвертьволновая пластинка, M1, M2 и M3 – зеркала, MO1 и MO2 – микрообъективы (40×, NA=0,65), C – ячейка с водным раствором с полистироловыми частицами, CAM – видеокамера CAM (TOUPCAMUCMOS08000KPB, размер пикселя – 1,67 мкм), I – осветительная лампа, L – двояковыпуклая линза с фокусным расстоянием 150 мм, M4 – полупрозрачное зеркало

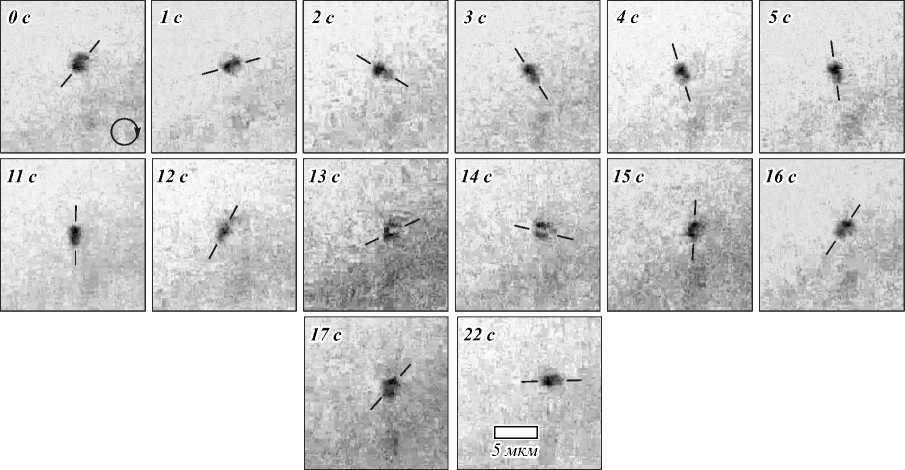
Рис. 7. Стадии вращения частицы, захваченной в сфокусированном Гауссовом пучке с левой круговой поляризацией. Линии указывают ориентацию частицы. Размер частицы – 2×1 мкм. Размер масштабной метки – 5 мкм

Рис. 8. Стадии вращения частицы, захваченной в сфокусированном Гауссовом пучке с правой круговой поляризацией. Линии указывают ориентацию частицы. Размер частицы – 2×1 мкм. Размер масштабной метки – 5 мкм

Из рис. 7 и 8 видно, что в фокусе Гауссова пучка с круговой поляризацией из-за спин-орбитальной конверсии формируется спиральный поток энергии, как и предсказывает уравнение (11). Этот поток энергии формирует продольную компоненту орбитального углового момента светового поля в фокусе, который передаётся захваченной микрочастице и вращает её по часовой (левая круговая поляризация, рис. 7) или против часовой (правая круговая поляризация, рис. 8). Заметим, что из (11) следует, что поток энергии в фокусе для левой круговой поляризации вращается по часовой стрелке, и на рис. 7 частица вращается по часовой стрелке. Также из (10) можно получить, что для правой круговой поляризации поперечный поток энергии в фокусе вращается против часовой стрелки, и на рис. 8 частица также вращается против часовой стрелки.

Заключение

В данной работе получены следующие результаты. На основе теории Ричардса–Вольфа получены аналитические выражения для потока энергии и распределения вектора плотности спина в остром фокусе вихревых лазерных пучков с линейной, круговой и азимутальной поляризацией. Из полученных выражений следует, что в фокусе имеют место следующие оптические эффекты:

• 1.    Спин-орбитальная конверсия, когда у исходного Гауссова пучка с круговой поляризацией нет ОУМ, а в плоскости фокуса у такого пучка есть отличный от нуля ОУМ (поперечный поток энергии). Поперечный поток энергии в фокусе равен по величине и по знаку поперечному потоку спина как для левой круговой поляризации, так и для правой. Оба потока (спина и энергии) вращаются вблизи фокуса по часовой стрелке (для левой круговой поляризации Гауссова пучка) и против часовой стрелки (для правой круговой поляризации Гауссова пучка). Экспериментально с помощью фокусировки (числовая апертура 0,65) лазерного пучка с длиной волны 532 нм, мощностью 100 мВт и круговой поляризацией продемонстрировано вращение полистироловой сфероидальной микрочастицы с размерами 1×2 мкм вокруг своего центра масс и вокруг оптической оси (полоборота за 12 с). При смене направления круговой поляризации Гауссова пучка микрочастица тоже меняла направление своего вращения.

• 2.    Орбитально-спиновая конверсия, когда при фокусировке оптического вихря с единичным топологическим зарядом и линейной поляризацией, у которого нет вектора спина, в плоскости острого фокуса появляется осевое распределение вектора плотности спина, причём в разных областях в плоскости фокуса вектор поляризации вращается в разные стороны: вблизи горизонтальной оси по

• 3.    Фотонные колёса или винты вертолёта. При острой фокусировке Гауссова пучка с линейной поляризацией в плоскости фокуса имеются поперечные составляющие вектора плотности спина (продольной составляющей нет). Если линейная поляризация исходного пучка была горизонтальная, то в плоскости фокуса вектор плотности спина направлен вертикально. То есть эллипсы поляризации лежат в горизонтальной плоскости, а вектора поляризации в этих эллипсах вращаются по разные стороны от оптической оси в разных направлениях (по часовой и против часовой стрелки). Такое вращение векторов поляризации в горизонтальной плоскости напоминает вращение винтов у вертолёта.

• 4.    Эффект полной магнетизации. При острой фокусировке оптического вихря с целым топологическим зарядом и азимутальной поляризацией (у такого поля нет спина) в плоскости фокуса вектор плотности спина (или спиновой угловой момент) направлен вдоль оптической оси. Поперечных составляющих у вектора спина нет. Это означает, что в плоскости фокуса лежат эллипсы поляризации. Направление вращения векторов поляризации (по часовой или против часовой стрелки) в плоскости фокуса чередуется от кольца к кольцу дифракционной картины в сечении пучка.

часовой стрелке, а вблизи вертикальной оси – против часовой стрелки. Вектор спина при этом в плоскости фокуса при обходе по окружности некоторого радиуса (350 нм) описывает поверхность Мёбиуса.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18-2920003) (параграф «Орбитально-спиновая конверсия в фокусе и лента Мёбиуса»), Российского научного фонда (грант 18-19-00595) (все остальные теоретические параграфы и эксперимент) и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) (параграфы Введение и Заключение).