Передаточные отношения эксцентрикового подшипника качения при ведущем наружном кольце

Цитирование: Меснянкин М. В. Передаточные отношения эксцентрикового подшипника качения при ведущем наружном кольце / М. В. Меснянкин, И. В. Кудрявцев, А. В. Колотов, А. Е. Митяев, А. В. Лысянников, С. И. Трошин // Журн. Сиб. федер. ун-та. Техника и технологии, 2024, 17(5). С. 642–654. EDN: GXTHJF заданного сложного закона движения выходного звена, что повышает их функциональные возможности.

Ведущим (входным) звеном эксцентрикового подшипника может являться одно из колец, внутреннее или наружное, которое задаёт движение его ведомым звеньям (телам качения, сепаратору) и располагается на неподвижной оси вращения. Выходным звеном принимается ведомое кольцо, на котором получают требуемое движение исполнительного органа технологической машины, а геометрическая ось этого кольца будет подвижна. При ведущем внутреннем кольце наружное кольцо совершает плоскопараллельное движение с определёнными кинематическими параметрами, а при ведущем наружном – внутреннее совершает движение уже с другими. Эти кинематические параметры и требуемое перемещение выходного звена ЭПК непосредственно зависят от характеристик его передаточных функций, определение которых является основной задачей предлагаемого кинематического исследования.

В связи с особенностями геометрического строения и нелинейностью движения звеньев эксцентриковых подшипников и механизмов качения (ЭПК и ЭМК) вопрос создания методов их кинематического расчёта и определения передаточных отношений усложнён и поэтому недостаточно подробно изучен. Большинство научных исследований посвящены определению кинематических параметров ЭПК и ЭМК с замкнутой системой тел качения диаметров как равной, так и переменной величины [9–17] лишь для случая преобразования вращательного движения входного кольца во вращательное выходного. Ранее авторами статьи в работе [18] определены зависимости передаточных отношений эксцентрикового механизма качения для случая преобразования вращательного движения ведущего внутреннего кольца в поступательное перемещение выходного наружного кольца. Однако в данной работе не было проведено аналитическое исследование полученных равенств и не показаны функции, определяющие закон движения выходного звена. Также полученные зависимости [18] не позволяют проводить кинематический анализ ЭПК и ЭМК при ведущем наружном кольце. Следовательно, для дальнейшего развития исследования кинематики эксцентриковых подшипников и механизмов качения становится актуальным решение задачи установления формул по определению передаточных функций для случая преобразования вращательного движения звеньев в поступательное при ведущем наружном кольце.

Цель

Целью работы является получение функциональных зависимостей по расчёту передаточных отношений от ведущего наружного кольца эксцентрикового подшипника качения, совершающего окружное вращательное движение, к его ведомым звеньям, а также выходному внутреннему кольцу, имеющему возможность поступательного перемещения. Результаты исследования позволят более подробно описать математическую модель кинематики ЭПК, выявить особенности его работы и способствовать созданию новых конструкций технологических цикловых машин, разработанных на его основе.

Методы

В проводимом исследовании используются существующие общепринятые положения прикладной механики и теории механизмов и машин, аналитические и графоаналитические – 644 – методы решения задач кинематического анализа, что в итоге позволило получить результаты в весьма простой аналитической форме, пригодной для использования инженерами при проектировании ЭПК и механических приводов на их основе.

1.    Кинематика движения звеньев ЭПК

При расчётах кинематических параметров эксцентрикового подшипника используются обобщённые координаты ведомых звеньев, зависящие от обобщенных координат ведущих колец как функции величин передаточного отношения. Рассмотрим решение задачи по установлению зависимостей, определяющих передаточные отношения и функции перемещения звеньев ЭПК для случая преобразования окружного вращательного движения входного наружного кольца в поступательное движение выходного внутреннего кольца, соединённого с исполнительным звеном рабочего органа механического привода цикловой машины.

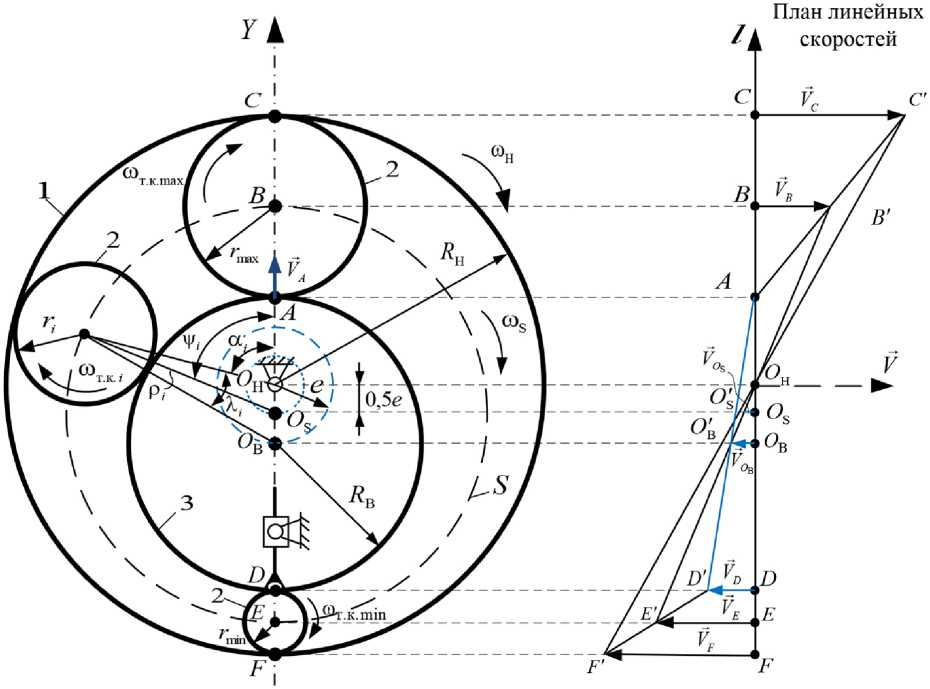
Составим схему движения звеньев ЭПК (рис. 1а) и примем следующие обозначения: е – эксцентриситет; R _B, R _H – радиусы дорожек качения внутреннего и наружного колец; r _max, r _min, ri – радиусы максимального, минимального и i -го тела качения; О Н , О В и О S – точки, принадлежащие геометрическим осям наружного кольца, внутреннего кольца и сепаратора.

В рассматриваемом случае движения (рис. 1а) ведущее наружное кольцо (звено 1) установлено на вращающемся валу, геометрическая ось которого (точка О _Н) неподвижна. Тела качения (звено 2) при их обкатывании без скольжения по дорожке качения наружного кольца будут взаимодействовать без скольжения с дорожкой качения ведомого внутреннего кольца (звено 3), которое является выходным и имеет ограничение от перемещений в окружном направлении относительно своего центра вращения точки О В . При этом внутреннее кольцо будет совершать колебательное движение в результате переносного движения его центра вращения по окружности радиусом, равным величине эксцентриситета относительно неподвижной точки О _Н (рис. 1а). Для наглядной оценки работы кинематики ЭПК выполним построение плана линейных скоростей (рис. 1б) для характерных точек подшипника, в качестве которых примем точки контакта тел качения с дорожками качения внутреннего и наружного колец, а также геометрические центры звеньев ЭПК (рис. 1).

Анализ схемы (рис. 1а) показывает, что точка А дорожки качения внутреннего кольца имеет возможность линейно перемещаться по оси Y вследствие переносного движения его центра вращения. Выходное кольцо ЭПК соединено с исполнительным звеном рабочего органа технологической машины в точке А , которая одновременно принадлежит и звену 2, т.е. телу качения максимального радиуса, контактирующему с наружным кольцом в точке С , скорость которой равна:

^C ^^тих ^т.к.шах,                                                       (1)

здесь ω т.к.max – угловая скорость тела качения максимального радиуса.

Относительная линейная скорость точки С (рис. 1) дорожки качения ведущего наружного кольца определяется:

V_c =V_F =R_n- ю_н,                                           (2)

где ωH – угловая скорость наружного кольца.

б

а

Рис. 1. Схема движения звеньев ЭПК (а) и план линейных скоростей (б) при ведущем наружном кольце

Fig. 1. Diagram of the movement of the EPC links (a) and the plan of linear velocities (б) with a leading outer ring

Сравнивая формулы (1) и (2), получаем выражение для определения угловой скорости максимального тела качения относительно своего центра вращения:

®т.к.тах — ®Н ’ _

^'тах

.

2.    Передаточные отношения ЭПК

Особенностью строения ЭПК [7] является смещение геометрического центра тела качения на угол клина λ i относительно точек О Н и О В (рис. 1а). Тогда угловая скорость ω т.к. i i -го тела качения равна:

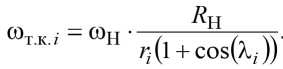
Анализируя (3), передаточное отношение ^12 от ведущего наружного кольца к телу качения определяется отношением угловых скоростей этих звеньев. В результате получаем:

.

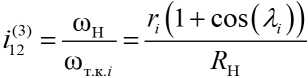
Относительную скорость точки B тела качения максимального радиуса выразим, рассмотрев прямоугольный треугольник Δ CAC ʹ (рис. 1б):

V_B=O,5-V_C =0,5-R„ -co .                                           (5)

Линейная скорость точки B , принадлежащая сепаратору, относительно неподвижного центра вращения ведущего наружного кольца, определяется по формуле:

V_B =®s-(pi-⁰^'c4l'/))

здесь ω S – угловая скорость сепаратора; ψ i – угол положения и ρ i – расстояние от центра i -го тела качения до геометрического центра сепаратора (рис. 1а).

В работах [7, 19, 20] определены зависимости и алгоритмы по расчёту геометрических параметров эксцентриковых механизмов с замкнутой системой тел качения, согласно которым угол ψ _i и расстояние ρ _i равны

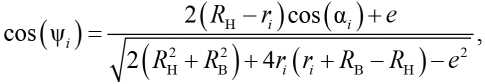
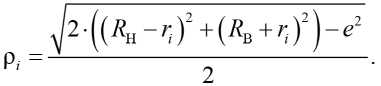
Угловая скорость сепаратора с учётом преобразований (5) и (6) равна:

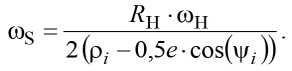
Тогда передаточное отношение ^i s) от ведущего наружного кольца к сепаратору при невра-щающемся внутреннем кольце определяется по формуле:

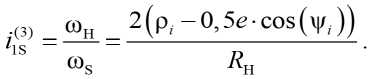
С учётом (8) выражение (10) после преобразований примет вид:

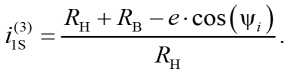
Скорость центра вращения сепаратора (точка О S ), совершающего переносное движение по окружности радиусом 0,5 е относительно неподвижной точки О Н (рис. 1а), с учётом (9) и (11), равна:

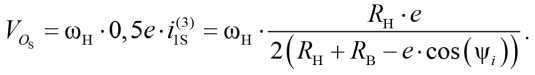
Из анализа плана скоростей (рис. 1б) следует, что переносная скорость VO_B движения центра вращения внутреннего кольца зависит от линейной скорости центра вращения сепаратора и его угловой скорости относительно центра вращения ведущего наружного кольца:

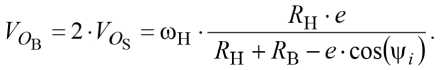
Вследствие переносного движения центра вращения внутреннего кольца точка А будет перемещаться по оси Y (рис. 1а). Смещение точки А зависит от углового перемещения ведущего – 647 – наружного кольца и сепаратора с обобщёнными координатами αi и ψi соответственно. Следовательно, при повороте сепаратора на определённый угол ψi точка А сместится по оси Y на некоторую величину, определяемую по формуле:

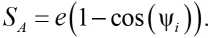
С учётом (7) величина линейного перемещения точки А при повороте наружного кольца на обобщённую координату α i определится по следующей зависимости:

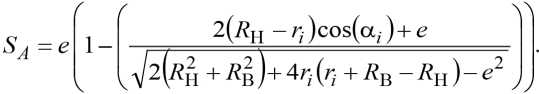
Скорость точки А получим, дифференцируя по времени (14)

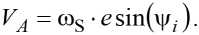
Линейную скорость этой точки в зависимости от угловой скорости ведущего наружного кольца получаем, выполнив преобразование (16) с учётом (7) и (9)

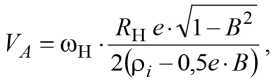
где

В = (о, 5с + (Л_н - /;)■ cos (а,))/р,

Анализ формулы (17) показывает, что передаточное отношение от ведущего наружного кольца, совершающего вращательное движение, к выходному внутреннему кольцу, совершающему поступательное движение (рис. 1) и соединённому с исполнительным звеном рабочего органа механического привода цикловой машины, равно:

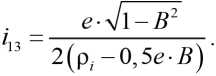
Полученные аналитические выражения позволяют проводить кинематический анализ ЭПК и определять оптимальное сочетание значений его геометрических параметров, которые обеспечат заданное передаточное отношение и закон движения выходного звена для рассматриваемого случая движения звеньев (рис. 1).

3.    Результаты расчётов

Выполним кинематические расчеты ЭПК, позволяющие качественно оценить получаемые параметры его движения. Используя выражение (15), построим в общем виде диаграммы (рис. 2) аналогов перемещения SA = f 1 (α), скорости dSA / d (α) = f 2 (α) и ускорения d ² SA / d (α)² = f 3 (α) точки А выходного внутреннего кольца как функции обобщенной угловой координаты (α) ведущего наружного кольца за один цикл работы ЭПК, который соответствует изменению этой координаты на угол от 0 до 2π.

По найденным формулам (4), (11) и (18) были посчитаны соответствующие передаточные отношения и построены функции их изменений (рис. 3 и 4) для схемы исполнения ЭПК – 648 –

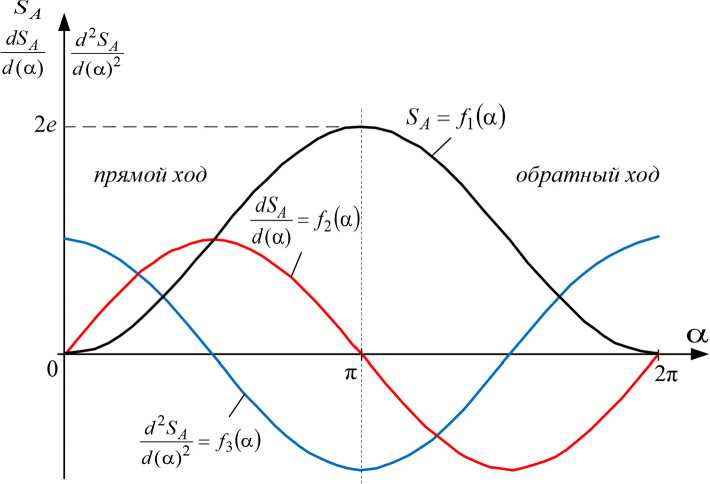
Рис. 2. Закон линейного перемещения выходного внутреннего кольца

Fig. 2. The law of linear displacement of the output inner ring

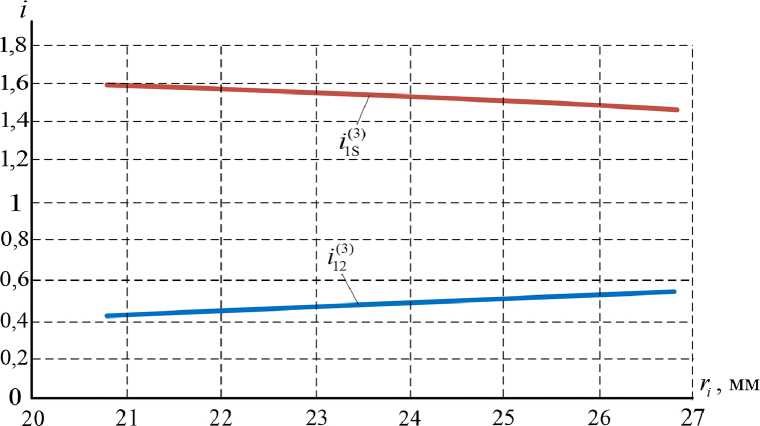
Рис. 3. Функции передаточного отношения ЭПК от ведущего наружного кольца к телу качения ^12 и сепаратору Z1S

Fig. 3. Functions of the ERB gear ratio from the leading outer ring to the rolling body 7'12 and separator

(рис. 1а) с расположенными на оси симметрии двух тел качения максимального и минимального радиусов в диаметрально противоположных направлениях [7, 8] и следующими значениями размеров основных геометрических параметров: e = 6 мм, R _B = 52,4 мм, R _H = 100 мм, r min = 20,8 мм, r max = 26,8 мм.

Кинематические диаграммы (рис. 2–4), анализ которых приведен далее, позволяют выявить основные аспекты работы эксцентрикового подшипника качения, а также наглядно оценить особенности его кинематики и ее влияние на движение выходного звена.

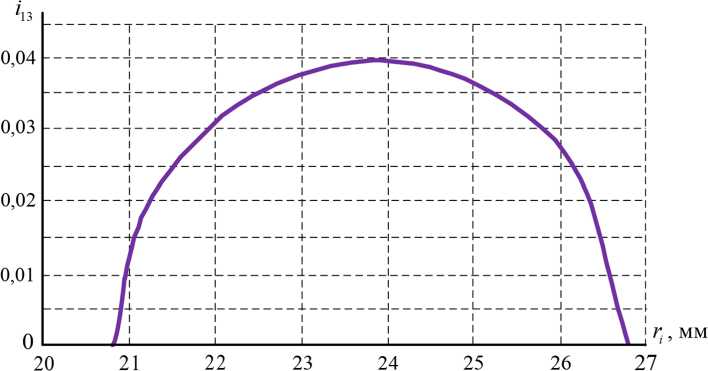
Рис. 4. Функция передаточного отношения ЭПК от ведущего наружного кольца к выходному внутреннему кольцу i 13

Fig. 4. The function of the EPC transfer ratio from the leading outer ring to the output inner ring i 13

4.    Обсуждение результатов исследования

Авторами статьи в данной работе получены уникальные формулы, показанные в простом аналитическом виде, позволяющие рассчитывать передаточные отношения эксцентриковых подшипников и механизмов качения при ведущем наружном кольце, а также определяющие закон его линейного перемещения. Формулы представлены как функции основных геометрических параметров и обобщённых координат звеньев ЭПК, что позволяет инженерам при проектировании механических приводов под заданные величины передаточных отношений варьировать или подбирать необходимые оптимальные сочетания значений размеров этих звеньев.

Проведём анализ полученных зависимостей и графических результатов их решения.

Если наложено конструкционное ограничение окружному движению выходного внутреннего кольца только лишь вертикальной прямой осью, соединённого с исполнительным органом технологической машины в точке А , то будем иметь простое линейное перемещение выходного кольца (рис. 1). При равенстве нулю величины эксцентриситета ( e = 0) ЭПК преобразуется в схему, подобную схеме радиального подшипника качения (РПК), геометрические оси внутреннего и наружного колец которого совпадают, а сами кольца могут совершать только вращательное движение, не имея возможности линейного перемещения. Следовательно, для РПК, или ЭПК при e = 0, передаточное отношение i ₁₃ должно равняться нулю. С целью проверки этого утверждения подставим в равенство (18) условие e = 0, в результате получаем ^Z13    % Г) ⁰ ,

■ / 2 A что подтверждает корректность выводов и достоверность полученных зависимостей.

При построении кинематической схемы ЭПК необходимо предварительно иметь законы движения его выходного кольца, получить которые для рассмотренного случая движения звеньев подшипника (рис. 1) позволяют функции (14)–(17). Их анализ показывает, что закон движения точки А выходного внутреннего кольца зависит от обобщённых координат (αi и ψi), а также геометрических параметров подшипника, в том числе и от величины эксцентриситета. При рассмотрении кинематических диаграмм (рис. 2) видно, что величина линейного перемещения (хода) SA точки выходного кольца равна удвоенному значению эксцентриситета, т.е. 2е, – 650 – а её путь перемещения делится на прямой ход и обратный, которые соответствуют изменению угловой обобщённой координаты ведущего кольца (α) на угол от 0 до π. Так как ЭПК имеет ось симметрии [7, 8], то законы движения точки А при прямом и обратном ходе получились симметричными (рис. 2).

Анализ функций передаточных отношений (рис. 3) от ведущего наружного кольца к телу качения /р и сепаратору ^1S показывает, что они имеют линейный закон изменения, а их величины от минимального тела качения к максимальному изменяются незначительно. Тела качения эксцентрикового подшипника обладают меньшими значениями радиусов, чем радиус дорожки качения ведущего наружного кольца. Следовательно, тела перекатываются по этой дорожке с большей угловой скоростью, чем вращается само кольцо, а значения передаточного отношения Zp получаются меньше единицы (рис. 3). Значения передаточного отношения ^1S получаются больше единицы (рис. 3), тем самым сепаратор, совершая окружное движение, вращается медленнее, чем ведущее наружное кольцо, выигрывая при этом в силовом факторе.

Функция передаточного отношения ЭПК от ведущего наружного кольца к выходному внутреннему кольцу i ₁₃ (рис. 4) изменяется плавно по схожему с синусоидальным закону. Анализ функции показывает, что значения передаточного отношения i 13 на минимальном и максимальном телах качения, расположенных на оси симметрии, равны нулю. Это позволяет при редукции скорости выходному кольцу и соединённому с ним рабочему органу цикловой машины выполнить останов и в следующий момент времени совершать линейное перемещение в противоположную сторону, т.е. делать прямой и обратный ход (рис. 2). Максимальные значения передаточного отношения i ₁₃ получаются на промежуточных телах качения ЭПК, расположенных на углу 90 градусов от оси симметрии. Следовательно, при повороте ведущего кольца на данный угол рабочий орган развивает максимальную скорость, а ускорение при этом будет равняться нулю, что подтверждается законами линейного перемещения выходного внутреннего кольца, показанными на рис. 2.

Для рассматриваемого в работе типоразмера эксцентрикового подшипника качения величина хода получилась равной S = 12 мм, а значения передаточных отношений от ведущего наружного кольца получились в следующих диапазонах: к телу качения Zp = (0,536 ÷ 0,416) к сепаратору Z^ = (1,464 ÷ 1,584); к внутреннему кольцу i ₁₃ = (0 ÷ 0,395). Необходимо отметить, что использование других схем исполнения ЭПК [7, 8] и изменение величин размеров его основных геометрических параметров будут непосредственно влиять на значения указанных диапазонов передаточных отношений подшипника.

При проектировании, на базе рассматриваемого в работе ЭПК (рис. 1), приводов машин с поступательным движением их рабочего органа инженеру необходимо учитывать, что максимальный предел линейного перемещения (хода) конструктивно ограничен и не превышает удвоенного значения эксцентриситета подшипника, т. е S max = 2 e .

Эксцентриковый подшипник выполняет функции опоры качения, эксцентрика и редуктора одновременно, что существенно упрощает структуру механического привода технологических цикловых машин, созданных на его основе. В отличие от зубчатых механизмов предлагаемый ЭПК обеспечивает закон движения его выходного звена (рис. 1, рис. 2), с изменениями значений передаточного отношения за один цикл работы (рис. 3, рис. 4) при гораздо более простой конструкции. Рычажные кривошипно-ползунные механизмы позволяют реализовать всего один вид – 651 – передаточной функции, наподобие показанному на рис. 4, и требуют введения дополнительных звеньев и кинематических пар. Достоинством ЭПК, по сравнению с рычажными механизмами, является отсутствие шатуна и возможность редукции с несколькими видами передаточных отношений (рис. 3 и 4), что позволяет сделать выходным звеном не только внутреннее или наружное кольцо, но и сепаратор, который будет выступать в качестве водилы. Эти достоинства предлагаемого эксцентрикового подшипника значительно расширяют функциональные возможности при его использовании в качестве рабочего органа механического привода.

Авторами статьи предполагается провести дальнейший анализ полученных кинематических зависимостей, выявить диапазоны передаточных отношений для различных типоразмеров и схем исполнения ЭПК, а также влияния изменения значений размеров основных геометрических параметров подшипника на величины и вид передаточных функций.

Заключение

В работе получены основные зависимости, позволяющие рассчитать значения передаточных отношений от ведущего наружного кольца ЭПК к его ведомым звеньям: к телам качения (4), к сепаратору (11), а также к выходному кольцу (18), для случая преобразования вращательного движения входного наружного кольца ЭПК в поступательное перемещение исполнительного органа технологической машины, соединённого с выходным внутренним кольцом подшипника. Полученные функции (14)–(17) определяют закономерности линейного перемещения выходного внутреннего кольца для рассмотренного случая движения звеньев подшипника. Выполненные кинематические расчеты и полученные численные результаты позволили определить типовые кинематические параметры эксцентрикового подшипника качения и качественно оценить особенности его работы.

Результаты работы позволяют обоснованно выполнять кинематические исследования ЭПК при проектировании механических приводов технологических цикловых машин, созданных на его базе, а также задавать необходимые сочетания геометрических размеров звеньев для обеспечения заданного закона движения выходного звена, что способствует расширению области применения и функциональному назначению эксцентрикового подшипника качения.