Переходные процессы в ортогональном ускорителе

Идея ортогонального ускорителя, гениально простая и плодотворная, сделала революцию во времяпролетной масс-спектрометрии [1]. Ей посвящено несколько теоретических работ, проясняющих основные принципы действия подобных устройств, но сказать, что при этом решились все насущные вопросы, никак нельзя [2, 3].

Основным элементом ускорителей служат плоские электрические зазоры, одинарные или комбинированные. Именно с их помощью удалось на порядки поднять разрешающую способность и чувствительность масс-рефлектронов. Подкупающая простота реализации определила их доминирующее положение в современной практике, однако оказалось, что в них не удается победить главный дефект ортогонального ввода ионных пакетов, а именно существенное временнóе расплывание ионного пакета за счет толщины вводимого в плоский зазор потока ионов и разброса их скоростей поперек зазора, т. е. вдоль оси ускорителя и в обратном направлении. Здесь возникает так называемое время возврата (или время разворота), которое дает значительный вклад во временнóе уширение ионного пакета на выходе из ускорителя. Временнóе уширение за счет конечной толщины ионного пучка можно существенно сократить, если перейти к ускоряющим полям квадратичного типа с гиперболическими электродами [4, 5].

Следует заметить, что и в ускорителе с плоскими электродами не все ясно с оптимальными режимами. В частности, неизвестно, можно ли уменьшить время возврата за счет зависимости от времени электрического ускоряющего импульса, реализуемого с помощью специальных генераторов.

Здесь, естественно, возникает вопрос о переходных процессах, которые возникают сами по себе в процессе зарядки емкости ускорителя. Как бы ни мала была постоянная зарядки (RC), картина ускорения ионов существенно зависит от нее. Успех перехода к квадратичным полям наводит на мысль, что нелинейные в пространстве поля могут дать варианты более эффективных схем ускорителей с компенсацией времени возврата. В данной статье мы исследуем все эти вопросы сугубо аналитическими математическими методами в весьма общей форме и обнаруживаем ряд эффектов, ранее в литературе не описанных. Цель данной работы состоит в том, чтобы нащупать принципиальные пути усовершенствования ортогональных ускорителей и при этом отсечь неоправданные иллюзии. Полностью проблему мы, разумеется, не решим, но надеемся достичь некоторого понимания этих сложных процессов.

• 1.    ПРЕОБРАЗОВАНИЕ ИОННЫХ ПРОЦЕССОВ В ОДНОРОДНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ

В однородном электрическом поле все будто бы просто, и новостей ждать не приходится. Однако мы относимся к этой банальной в большинстве случаев ситуации с неким мистическим благоговением, как и к случаю потоков в бесполевом дрейфовом пространстве. Плоский конденсатор в условиях стационарного или переменного во времени электрического питания — безусловно, самый простой электронно-оптический элемент и в тоже время самый загадочный в силу универсальности его применения. Здесь — энергоанализ и времяпролетная масс-спектрометрия, электрон- ные лампы и СВЧ-приборы, интегральные способы анализа и электрический удар, и многое другое. Исчерпано ли все это богатство? На наш взгляд — нет. Более того, мы пришли к выводу, что по-настоящему, во всей полноте трансформационные свойства однородных полей вообще не изучались. Все происходило как бы между прочим, в контексте той или иной конкретной задачи. Между тем, когда речь идет о каком-нибудь сугубо неоднородном поле, математические трудности никогда не позволяют преобразующие свойства поля представить с должной общностью, и в этом смысле однородное поле есть безусловный уникум. В этом разделе мы подробно рассмотрим две типичные ситуации ("стационарная" и "нестационарная"), которые обычно реализуются в системах поперечного ввода ионных пакетов во времяпро-летный масс-спектрометр (TOF-MS). Дело это считается едва ли не общим, тривиальным местом, хорошо изученным и привычным. Но так ли это?..

x = q -^- • — + v_nt + x ₀.                 (2)

ml 2   ^{0    0}

Обозначим t_k — момент пересечения иона с гранью x = 0, v_k — скорость в момент пересече- 2

ния и Ek = m vk — конечная энергия. Вычислим все эти величины. Из-за простоты ситуации мы пользуемся размерными величинами, чтобы сильнее почувствовать в этой привычно-банальной обстановке "физичность" всех этих как будто бы тривиальных процессов. Итак, пишем условия пересечения x = 0 в виде

v lm    x lm

t2 + 2-0— t + 2-0— = 0.

qΦ ₀     qΦ ₀

Откуда

Случай 1, стационарный

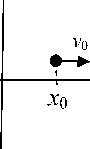
Рассмотрим плоский конденсатор в соответствии с рис. 1, в котором движется ион с зарядом q и массой m , стартовавший из точки x 0 со скоростью вдоль оси x величины v 0 . Конденсатор находится под напряжением Ф 0 , выталкивающим ионы в положительном направлении оси x . Компоненты начальной скорости вдоль пластин конденсатора примем нулевыми.

Движение иона определяется уравнением и начальными данными (1):

t =

v 0 ^lm ± qΦ ₀

' vjm

I qф o

₂ x ₀ lm qΦ ₀ ^.

Поскольку x ₀< 0 в нашей системе отсчета, то выбирая положительный корень, запишем

4 =

^f v 0 lm Y + 2 1 x el ^ml _v q ^ф o J      q ^ф o

v ₀ lm

. qΦ ₀

Далее вычислим скорость в момент пересечения t_k :

Из (1):

-l

Ф 0

d2x   Φ m—г = q  , dt2 l

x l t = 0 = x 0 ,

d x d t

t = 0

d x

vk = dt

,

^t = 4

= v 0 .

qΦ

Vk = ^4 • ^{t +} v 0 ml

0 =

y

x

Рис. 1. Расположение иона при старте в плоском конденсаторе

qΦ ₀ ml

' ^v 0 ^lm ) + 2 I ^x 0I ^ml - v ti lm _v q ^ф 0 J     q ^ф 0 q ^ф 0

v k =i v² 0 ^{2 +} 2| x d • q^Ф7• ml

Кинетическая энергия в момент t_k :

„   mv2 m f 2      1 qФ

E, =     = b02 + 2 xn k 2      2 1 0     1 01 ml mv02      qΦ0

= 2 + lx01 • l •

> + v0,

Пусть

x = 1,

x ₀ , x ₀ ,

E о = m • у.                  (9)

Тогда

E k = E о + Ф x о|.           (10)

τ ²

•.

x = —+ x_от + x _о;

τk

—

x ₀,

x k = V x  ² x о ,

Все эти привычные соотношения можно было бы писать сразу же по памяти, но наш опыт подсказывает, что при этом мы можем проглядеть простые, но весьма важные вещи.

Например, аналитическая функция (5) имеет особенность при Ф 0 →0, и надо рассматривать предел. Имеет смысл поэтому преобразовать (5) к другой форме, домножая на сопряженное:

Положим

t k =

' v о lm Y + 2 | x o| lm l q^ J     q^

' v o lm l ЧФ о

^f V 0 lm ) + 2 1 x о l ^lm ₊ V o lm i qФ o J      qФ o qФ o

wk =

² x ₀

—

x 0 .

^w o =

² x ₀

.

И приведем (16) к виду

xk

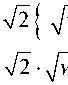
x ₀ ,

—

w k = ^w o ^{— x} о ,

x _о <  о.

2 x ₀

\I^v о ^{2 + 2}| x о I ^{Ф + v} о lm

В этой форме становится прозрачным процесс изменения t k по мере исчезновения поля Ф 0 →0.

Из обеих формулу (5) и (12) одинаково видно, что если частица "легчает" ( m ^о), то t k ^ о. Однако для очень тяжелых частиц ( m →∞) формула (5) опять дает неопределенность (∞ – ∞), в то время как из (12) видно, что с ростом m влияние поля Ф 0 становится все меньше и движение при малой скорости v 0 , если Е 0 = const, приближается по свойствам к дрейфовому.

Знак перед радикалом w в (13) должен совпадать со знаком ,т _о. Заметим, между прочим, что формулы (16) дают гладкую относительно ,т _о аналитическую функцию, а (18) относительно w терпит разрыв по производной в нуле. Факт примечательный, который не следует упускать из вида.

Физическое время t_k на грани x = 0 получается из (13) и (18.1)

t k = l

2 m

■(v w q ^ф о ^v

—

x _о ± V w ) .

Безразмерная модель

Все-таки в этих размерных физических формулах есть какая-то математическая несуразность, не отвечающая сути проблемы, поэтому мы вернемся к своему обычному порядку, положив

X = lx , t = T t , T = l ----;        (13)

,        ,         2Φ0

x

о =

X 0 l ^,

T xо = lv о.

Тогда имеем:

В сущности, это выражение характеризует своеобразный масс-спектрометр, который надо встраивать в общую схему оптической системы TOF-MS, например масс-рефлектрона. Нам кажется, что обычный способ рассмотрения самого оптического тракта TOF в отрыве от выражения (19) принципиально неверен. Плоский конденсатор сам по себе деформирует ионный пакет и частично разделяет его по массам. Будучи пристроен к какому-либо "времяпролетнику", он может менять в целом фокусирующие свойства тракта по энергии, и все это надо прогнозировать.

Рассмотрим теперь, что же конкретно мы имеем на грани x = 0 после того, как ее пересек ионный пучок в виде бруса a < |xо| < b                   (2о)

с распределением энергии о < w < 5.                 (21)

Здесь нам в первую очередь интересно определить максимальный размер интервала во времени Ат_к , в течение которого ионы из бруса (20, 21) пересекают грань x = 0. Для этого нам необходимо изучить мах и min функции

^T k = V2 {T w +Ы ± V w }         ⁽²²⁾

при условиях (20, 21). Нам еще раз хочется подчеркнуть, что выражение (22), в сущности, описывает две функции, сливающиеся в нуле w = 0, а полный размах τk может включать в себя значения из обеих ветвей. Вполне очевидно, что му, несмотря на конечную толщину пучка (b – a). Из этого можно сделать вывод, что имеет смысл отодвинуть ионный пучок подальше от грани x = 0 и стараться сделать толщину его (b – a) как можно меньше. При этом уменьшаются обе величины Аwk и Атк .

Случай 2, нестационарный

Запитаем пластину X = – l переменным напряжением, и потенциал Φ запишем в виде

( t 1 X Ф = -Ф f —--

⁰ ( T) l

.

max τ_k min τ_k

= V2 { v 5 I b + 4зу = V2 {V 5 + a - лу

Разница этих величин:

Ат_к = V2{ 45+b - V 5 + a + 2 45^ =

Б / ^b - a и .<1

= ^V2 I Л^:---7Г= ^{+ 2V 5} I .     (24)

[ \5 + b + V 5 + a

Безразмерная функция f задает временнýю форму электрического питания, а Т — ее временнóй масштаб. Для стационарного случая f = 1. Если предполагается что напряжение ограничено по величине при всех t , тогда имеет смысл конструировать f так, чтобы ее максимум был 1. Если мы изучаем ход напряжения с неограниченным ростом, то выбор f надо сообразовывать с частными обстоятельствами. Запишем уравнение движения в данной ситуации и начальные данные:

В течение этого времени ионы пересекают грань x = 0, будучи частично диспергированными по массам m и приобретя при этом дополнительное ускорение. Кроме того, происходит трансформация энергии в соответствии с формулой (18). Полагая x ₀ = b и w = 5 , получим

d2X  qΦ m—т- = —0 dt2 l

;

^X|t = 1 0 = ^X 0 , d X -l t = 0 = v 0 .

Сделаем запись безразмерной:

max w k = 5 + b

и, полагая x ₀ = a , w = 0, получим

X = lx ,

Получим уравнения:

t = T • т .

min w k = a .

^x = ql4 • f ( ^т ) •

Отсюда разность ( max w k - min w k ) принимает значение

x

= _x = X ⁰

т 0 = T      ⁰ l ’

x

_ t 0     x ⁰

^т 0 = t

Tv 0 l

.

A w_k = 5 + ( b - a ) .

Конечная величина толщины бруска ( b – a ) увеличивает энергетический разброс A w_k на выходе из конденсатора. Если пучок очень тонкий ( b - a ) = 0, то энергетический разброс сохраняется на уровне ( 0, 5 ) . Из (24) при ( b - a ) = 0 получается, что выходная длительность имеет min и отвечает чистому времени разворота ионов

Ат_к = 2425.

В отличие от стационарного случая у нас здесь нет возможности ввести скользящий масштаб времени T, зависящий от масс ионов m. Теперь Т — замороженная величина, как и l. Мы можем оставить в уравнении движения коэффициент перед f (т) таким, каков он есть, но, в принципе, можно ввести специальную единицу измерения массы m0 , положив m = m0 • ц,                 (33)

и далее наложить условие на выбор m ₀

Если увеличивать b и a так, чтобы разность (b – a) сохранялась, то дробь в (24) постепенно уменьшается и Атк стремится к своему миниму- q^T2=1. m0l2

Тогда уравнение динамики будет fτ x = ^-),              (35)

µ

а начальные данные остаются прежними, но что при этом происходит с энергией?

mv 0     m о l ² x 2

En              LI        * .

⁰    2 T ²   2

Заменяя из (34), получим

E о — 2 Ф ₀ * ^^,

или

Таким способом мы получим скользящую шкалу масс, связанную с энергетическим параметром поля Φ ₀ . Удобно ли это, все зависит от исследуемого диапазона масс ( m 1 ÷ m 2 ). Ему будет отвечать некоторый интервал безразмерных масс ( μ 1 ÷ μ 2 ). В целом условие (34) выглядит каким-то искусственным. Можно было взять и какое-нибудь другое число вместо единицы, но тогда "поплыло" бы соотношение (38), а оно имеет ясный физический смысл, так что надо признать, что в таком варианте "обезразмеривания" есть доля привлекательности. Однако сейчас мы предпочтем положить

Для разных m мы имеем и разные λ, так что сценарий движения ионов с разными массами в нестационарном поле тоже разный. Интегрируем (41) с учетом начальных условий.

Пусть F (т) — первообразная для f j f (т) dт — F (т) + const.(42)

Тогда x - x — X{ F (т)-F (то)}.(43)

Положим

Q — j F (т) dт + const(44)

и проинтегрируем (43), получим окончательно x — XQ(т) + {x - XF(то )}(т - то) +

+ {xо - XQ(то)}.(45)

Обе первообразные F и Q определены с точностью до const, что вносит в структуру (45) некий привкус психологической зыбкости, которая, конечно, пропадает при конкретном выборе функции f ( т ) . Какие вопросы можно решать с помощью нестационарного режима работы плоского конденсатора? Нас, конечно, будет интересовать сокращение A t k на ионном пакете при выходе через грань х = о, снижение As k .

Пример, f — e ^a

X —

qΦ 0 T ² ml ²

Здесь

вид

F — —e^a , Q — -*y e ^a , тогда (45) примет α       α ²

и не вводить никаких особых единиц для массы m .

Теперь связь начальной энергии E ₀ , выраженной в какой-нибудь обычной системе физических единиц с выбором местных масштабов l и T выразится формулой

E о —

mv ₀² 2

f"1

9 T ² I

V ^{2 T} )

² x 0 .

x — A ( e ^a - e ^{a о} ) + | Х _о - ^X e ^{a о} | ( _T - т _о ) + x _о.   (46)

a ^{x 7} V a )

Возьмем то — о x — А(ea -1) + | ;ёо - AL + xо.      (47)

a ^{v 7} V ^a )

Коэффициент при x 2 можно рассматривать как некую характерную энергию иона, в долях которой выражается безразмерным параметром x 2 величина E ₀ . (Кажется странным, что не величиной ²

x _{0 )}

Итак, пишем x — Xf (т).                   (41)

Условие перехода иона на грань х = 0 дает уравнение относительно момента пересечения τ_k . Положим x ₀< 0 и запишем

^A ( e ^a - i ) + f Х о - ^A | т -| x о| — о. (48) a ^{x 7} V ^a )

Уравнение трансцендентное, и просто так его не решить относительно τ . Для простоты положим a — 1 и запишем X( ет - т -1) + .x0 - |xо| — о, или e - т -1 =

I ^X 0 ^{- X} 0

λ

Корень τ зависит от одного объединенного параметра. Уже интересно, что одному корню T k = const отвечает многообразие масс и начальных данных, связанных линейным соотношением

| X0| - X0 = cX.(50)

Если записать общий случай (45), то получим

^{X Q} ( ^т ) + { ^x 0 ^{- X F} ( ^T 0 ) } ( ^{T - T} 0 ) ^-

• -|Xo| - XQ(T0 ) = 0.

Перепишем это в виде

^X { ^Q ( ^T ) ^- F ( ^T 0 )( ^{T - T} 0 ) ^{- Q} ( ^T 0 ) } = I ^х o| ^{- X} o , ⁽⁵²⁾ или

• Q(T)- Q(T0 )- F(T0 )(T - T0 )= 'x0!. x0 .

λ

Вывод

Ни при каком профиле нестационарного электрического питания f ( т ) в плоском конденсаторе невозможно ликвидировать время разворота ионов.

Такой эффект в чистом виде следует искать в классе пространственно-неоднородных полей с переменным во времени электрическим питанием.

Однако можно надеяться на уменьшение времени разворота ионов уже в сильно неоднородных полях даже в условиях статического ускоряющего напряжения.

2. ПРЕОБРАЗОВАНИЕ ИОННЫХ ПАКЕТОВ В НЕОДНОРОДНЫХ СТАЦИОНАРНЫХ ПОЛЯХ

Вместо однородного поля рассмотрим одномерный потенциальный рельеф

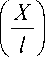
Появление обобщенного параметра справа, как и в (49), есть общее свойство данной структуры.

Могут ли два иона с противоположными скоростями ± |. x ₀|, стартующие с фиксированной точки ( x 0 ), достичь грани в один и тот же момент τ_k . Для этого должны выполняться два равенства:

и изучим движение при тех же начальных условиях. Физические уравнение движения d2 X       дф m    = - qф            (56)

d t ^{2     4 0} д x             ^v ’

^Q ( ^т к ) ^{- Q} ( ^т о ) ^- F ( ^т о )( ^T k ^{- т} о ) = I ^x 0! I ^х 0!

λ

X 0 + KI

^Q ( ^T k ) ^{- Q} ( ^т о ) ^- F ( ^T 0 )( ^T k ^{- T} 0 ) =

и начальные данные приведем к безразмерной модели теми же подстановками (13, 14). В результате запишем

Но левые части одинаковы и, следовательно, не могут давать справа неодинаковые числа.

X = lx , t = Tt ,             (57)

..     ^d ф ( x )

^X =--^, ^X т = 0 = ^X 0 , ^X т = 0 = ^X 0 .         ⁽⁵⁸⁾

d τ

Интеграл энергии:

Отсюда

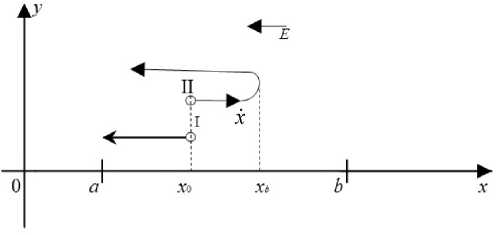
Рис. 2. Возникновение "времени разворота" для ионов I и II

^{+ ф ( X} ) - g ,

_XC² g 0 = -70-⁺ ф ^{( X} 0) ,

■^X o²

IT= ^w 0 .

1 ^x     d x

T = —T I /          •.

V2 X о V g ^- ф ( ^X )

Пусть

— >  0 при x >  0

d x                                (61)

и a <  x 0 <  b ,   0 <  w <  5.

Изучаем время полета ионов (рис. 2) до грани x = 0 при условии разброса начальной скорости в интервале

- 72 5 <  x ₀ < 72 5 .            (62)

Для иона I имеем условие полета до грани x = 0:

1 ⁰     d x

² x 0 7 g - ф ( x )

x ₀

d x

52 0 7 g ^- ф ( ^x )

Для иона II время полета складывается из двух частей:

1 x b     d x         1 0      d x

V2 x 0 7 g ^- ф ( x )  ²2 x₆ 7 g ^- ф ( ^x )

ном росте ф ( x ) определяется с помощью интеграла энергии и, очевидно, будет определяться неравенством

ф ( a ) < w k <  5 + ф ( b ) .              (69)

Соответственно разброс A w k :

0 w k <  5 + [ ф ( b ) - ф ( a ) ] .               (70)

Поведение Ат_к и A w k может оказаться весьма различным при фиксированной толщине пучка ( b-a ). Чем круче ход ф ( x ) , тем больше A w k , и в тоже время величина Ат_к может оказаться существенно меньше, чем в плоском конденсаторе, если ф ( x ) некая нелинейная функция. Сказать, какой именно должна быть функция ф ( x ) для уничтожения Ат_к или хотя бы уменьшения ее до приемлемых размеров, достаточно трудно. Во всяком случае никаких абсолютов на данном этапе просто так нам не найти. Математическая проблема здесь весьма нетривиальна. Прояснить ее могут разные частности.

x b

x ₀

d x        x 0      d x

² I / b +1 , b J . _ x 0 7 g - ф ( ^x )    0 7 g - ф ( x )

Квадратичное поле

Положим

Окончательно можно записать

Ф = ax ².

T II = V2 J     ^d x + T I .

x 0 7 g - ф ( x )

Вычислим сначала интеграл:

xb

d x

При фиксированном x ₀ длительность ионного пакета на выходе через грань x = 0 определяется чистым временем разворота иона в поле

x ₀

—

αx ²

xb xa

г

- arcsin

A

α x ₀

x b     _{d x}

^{( A T} ^ ) x „ = const = ^T II - ^T I = J ,            .       ⁽⁶⁶⁾

x 0 7 g — ф ( x )

к

'0 7

arccos

Полная же длительность ионного пакета на выходе при конечной толщине бруска ( b–a ) и разбросе (0÷ δ ) энергии w должна определяться через min t , и max t II :

w

^{1 +} — 2 αx ₀ ²

=. — arctg α

w

.

Далее вычислим интеграл (63):

xb

А т_к = max t II - min t I .

τI

d x

g - axx

x 0 α

Для вычисления интегралов (63) и (65) нужно указать конкретный вид ф ( x ) . Координата величины определяется из уравнения

arcsin x 2 α

g ^- ф ( ^xb ) = ^{0.                (68)}

Соответственно из (65) и (72)

Интервал энергий w_k на выходе при монотон-

2      1 w π

^T "■ 7 ^arCtg x 7 ⁺ 2k2

Поскольку т I = const, то остается найти max т II ,

а он вполне очевиден. Надо только положить

Атk =

2 δ

w = 5 , x 0 = a , тогда

2      1δ max т II = — arctg— — α    aα

b ² - a²

А w k - 5 ’

и

окончательно

или

Ат_k -(А w_k - 5 ) = 72 5 ( b ² - a ² ) .        (80)

^{А т} k = J² arctg ¹ J ⁵ • α aα

Если брать бόльшие a и α при достаточно малом 5 , то Ат_k можно сделать сколь угодно малым, но ценой этого будет огромный рост А w k :

А wk = 5 + а (b2 - a2) = 5 + а( b - a)(b + a ).   (76)

Получилось нечто вроде соотношения неопределенности. Величины Ат_k и А w_k оказались взаимно обратно пропорциональны, и связь их не зависит от крутизны рельефа α , по крайней мере для квадратичной функции ф ( x ) . В этом новом свете мы должны вернуться к однородному полю и посмотреть, что делается там.

Если скобка ( b – a ) остается постоянной, то с отдалением границ пучка растет скобка ( b + a ); она и задает рост А w k . Между Ат_k и А w k явно

Однородное поле

Положим ф = ax и вычислим т I и т II :

присутствует какая-то внутренняя связь в виде некого инварианта. Одно растет, другое падает и наоборот...

Какова природа этой связи, и какую фундаментальную роль играет выбор типа функции ф ( x ) ? Может быть, она следует из классических инвариантов механики?

Пока мы будем искать ее на частных примерах.

Так, в нашем случае квадратичного поля параметр α характеризовал явно крутизну рельефа, в то время как ф ( x ) характеризует и крутизну, и кривизну. Чтобы менять крутизну, достаточно менять α , в каком бы месте оси x мы не находились. Кривизна же сильно зависит от места x , и она определяет качество фокусировки по времени. Однако сейчас мы можем поставить вопрос так: в чем состоит влияние крутизны α на соотношение между А w k и Ат_k в данном случае и есть ли оно вообще?

Выразим α из (76)

^т II = ^т I ⁺

x ₀

d x

а =

А w k - 5 b ' - a ²

и подставим в (75), получим

АЧ =

2 (b2 - a2)

А wk - 5

1 arctg α

5(b2 - a2)

А wk - 5

Очевидно, что А w k будет конечной величиной, даже если 5 = 0. Это происходит за счет падения потенциала на толщине пучка ( b – a ). Если предположить что δ очень мала, то можно отождествить величину arctg с величиной под знаком этой функции:

1 ^{x 0}    d x

V2 о V g - ax

—

αx ₀

J к ах ^т I + о \^{g - ax}

Объединяя, получим

^т II =

w . α

Соответственно Ат_k = max т II - min т I выразит-

ся формулой

Ат_к = — (V 5 + ab - V 5 + aa + 2^ ) .    (84)

Если сравнивать (75) и (84), то при достаточно больших a и фиксированной толщине пучка ( b – a ) при одних и тех же δ и α квадратичное поле дает гораздо меньшую величину Ат_к , чем однородное. Найдем теперь А w_k :

А w_k = 5 + а ( b - a ) . (85)

Если сравнивать с квадратичным вариантом (76), то там разброс А w_k гораздо больше, и он растет с удалением пучка ( x ₀ ^ да ), в то время как в однородном варианте он определяется только толщиной пучка и крутизной α . Чем больше α , тем больше разброс А w_k , и из (84) следует, что тем меньше Ат_k . Однако опять можно исключить α из (84) и (85) и получить связи

a =

A w_k - 5 b - a

ф = ax ,

Запишем (84) в виде

42 f      a bb - a)             1

Атк = — ^ ,    (--+ 2V5 к a I 55 + ab + 55 + aa       I

где положительный показатель n может меняться в широких пределах от 0 до сколько угодно больших (0 <  п < да ). Записываем

Подстановка α из (86) в (87) дает искомую связь Ат_к и A w_k , не зависящую от крутизны рельефа α :

1 x0     dx v 2 о 7g - axn

n g = w + ax о ,

т II = T i + V2j           .

n x 0 5g ^{- a x}

^А Ч =

( b - a ) ⁷²

^ b Ат_к - a5 + J a A w_k + b5 - 2 a5

+

+ 2 45 ( b - a ) _>  ^A w k ^{- 5}   "

При достаточно больших a и b и небольшой разнице ( b – a ) первым членом в (88) можно пренебречь и записать эту приближенную связь в виде

Ат_к -( A w_k - 5 ) = 2425 ( b - a ) .     (89)

Сравнивая с (80), мы видим, что при одинаковых избытках разброса энергии ( A w_k - 5 ) , если поделить (80) на (89), можно получить

( А т )     Ь-а

) ^k (^квад. = __             (90)

^{(A T} k ) одн. ²

Понимая всю достаточность приближенных замен, все же надо думать о природе всех этих вещей более глубоко, ибо из (90) следует, что для двойного уменьшения AT_k в квадратном поле по сравнению с однородным надо брать a и b из условия

a + b <  1. (91)

Получается, что крутизна рельефа α играет значительную роль в уменьшении времени AT_k , но в большей степени влияет кривизна рельефа. Все это побуждает изучать этот вопрос со всей тщательностью и в самом общем виде.

Все-таки, насколько можно уменьшить AT_k без существенного уширения энергетического разброса A w_k , если рассматривать весь класс неоднородных монотонно растущих рельефов в целом?

Степенные поля

Рассмотрим класс потенциальных рельефов ф ( x ) вида

Если n ≠ 1, 2, то интегралы (93) не берутся в элементарном виде, и приходится прибегать к разным аналитическим оценкам. Для начала введем замену переменной интегрирования

и учитывая, что лы (93) к виду

• ^ ,

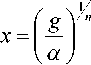
^ 0 = x 0 •

^т i =

Г a ) n

— I , приведем интегра- l g )

1 g" 2 ( °    d ^

4i _a n j TT - T n

g n ^{2 1}

^т ii = ^т i + V2   — j

α^{n ξ 0}

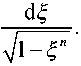
Эти интегралы (95) следует брать по следующей схеме. Сначала берется несобственный интеграл

J = ¹ d

° jJT-

n

1 n

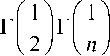
г | - + -

1 2 n

где Г — гамма-функция Эйлера. Далее вычисляется собственный интеграл

ξ 0   _{d ξ}

J ¹ UT -

Для ( ₀< — и больших n дробь , можно ² 71- T ”

разложить в степенной быстро сходящийся ряд, после чего интеграл J ₁ вычисляется в виде ряда по степеням ξ ₀ . Имеем:

n

1  3,5,

= 1 + - К + 3 К2 n + — К3 n + ■•,

2      8       16          ^,

1                    3

n + 1                     2^ n + ¹

¹ = ^ 0   2 ( n + 1 ) ^ 0     8 ( 2 n + 1 ) ^ 0

Конечно, здесь так же можно избавиться от крутизны a и найти связь Ат_к и A w_k , но ввиду того, что построение это приближенное, то и смысла выводить данное соотношение никакого нет.

I5_______ к 3 n + 1

16 ( 3 n + 1 ) 0°

+ • •.

Пусть n = 4, тогда

J_t = К + — К 5 +— К 9 + — К + -•      (99)

1    0 10 0   24 0   238 0

"Радикальные" рельефы

До сих пор мы рассматривали рельефы выпуклые вниз. Однако при n < 1 степенные рельефы выгибаются дугой вверх, и интересно, как они работают.

Положим

Быстрая сходимость этого ряда вполне очевидна. Для достаточно больших n члены ряда убывают достаточно быстро, так что для оценок можно пользоваться только первым членом. При фиксированном n J ₀ представляет собой const, которую раскрывать не будем. В этих предположениях запишем τ _I и τ _II :

Ф = a

x .

В нуле этому рельефу отвечает бесконечное поле, и в окрестности нуля ион летит малое время. Несмотря на физическую несуразность, в математическом отношении оценки получаются вполне конкретные, ибо область нуля всегда мешает. Снова вычисляем τ _I и τ _II :

x ₀

^т i

2 g

1 x0     dx т i=^=j ,       , g=w+a x °

32 °^g-aVx

^т ii =

x ₀

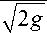
g

α

J 0

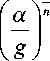
x ₀

т ii = т i + V2 J x° Ng — aVx

= V2

g

Интегралы эти легко берутся заменой a V x = u , и получается

J 0

α

.

2 g

Полагая g = w + ax ° :

x 0         ,

J 2 ( w + ax 0n )

22   3

^т i = —т { 2 g - g--ax ° • ( ² g + ax ° ) } , ³ α                                    (105)

^T ii = ^T i ⁺ 3a?' ^ g ^{- a}^x ° ’ ( ² g ⁺ ax ° ) .

Окончательно мы получим следующие форму-

1 1

( w + ax n ) ^{n 2}

^T ii                        1 J °

αn

лы, раскрывая еще g = w + a^/x ^" , но сначала вста-

x ₀

вим τ _I в τ _II . Получаются весьма симметричные формулы

Получаем интересную картину: при n > 2 с ростом x ₀ обе величины и τ _I , и τ _II убывают и тем более убывает их разница, однако, увы, и здесь с ростом a и b на естественный разброс ионов в пучке накладывается растущая полевая надбавка

A w_k = 5 + a ( bⁿ - a" ) . (102)

^T i =

α ²

^T ii = —— α ²

g - a

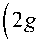
g - a

Подставим g и получим:

тI =

22 α ²

2 ( w + aJX 0 ) ² -

272          /г\ 32

maxтII =—=-<213 + ab) + a I v ’

- 7w •( 2 w + 3aJX0 )j,

272 r / .              .

т II =—5—! 2 ( w + adx ₀ ) + a I ^v              ’

Отсюда

.

I

+ Vw •(2w + a]x0 IV

Теперь ищем min τ _I , когда скорость направлена в сторону x = 0, X <  0, энергия w = 3 , а координа

Атк =   2

α ²

2 (3 + ab)'5

—

— (3 + Oa)

+

та старта минимальна, x ₀ = а .

22 min т I =—— α ²

- 73 •( 23 + 3a4a )k     (108)

2 (3 + aVa) —

Остается найти A w_k :

A wk = 3 + a( 4b — 7a).

Соответственно

Можно и здесь исключить α , чтобы получить связь Ат_к и A w_k , но она слишком сложная, и есть ли в этом необходимость? Положим а = 1 и упростим эти формулы:

Ат к = 242 <2 (3 + 4ь)/2 — (3 + 44)

+ 4 3 ³² + 3 43 ( 4b — 4а ) [ ,

А wk

= 3 + (4b — 4а ) = 3 +

b — а

.

Ч b + V a

Если сильно отдалить a и b , так чтобы разность ( b – a ), толщина пучка, сохранялась, то

A w_k ^ 3 ,    Ат_к ^ 872 3 32 ;    (113)

из (87) для однородного поля при а = 1 и при тех же условиях роста a и b

Ат_к ^ 2423.            (114)

Как это ни удивительно, отношение величин (113) и (114) равно 43. Если 3 = 0.01, то в рассмотренном варианте Атк в 25 раз меньше, чем в плоском конденсаторе, и при этом добавка энергетическому разбросу сильно уменьшена. Конечно, это только качественная оценка, но все же факт, не совсем понятный физически. Может быть, все дело в том, что мы считаем a и b слишком большими величинами и рассмотрение приобретает асимптотический характер. Некоторая странность во всем этом есть. Поля с потенциальным выгибанием вверх не должны уменьшать Атк, хотя Аwk при фиксированной величине (b – a) для таких полей меньше, чем в плоском конденсаторе.

Электрическая стенка

Рассмотрим рельеф вида

α

Ф =-------7.

(в — x )2

Потенциальный рельеф неограниченно растет при x ^ в (рис. 3), образуя гладкую стенку. Вычисления с таким рельефом отличаются тем, что x_b <  в . В данной структуре, меняя α и β , мы можем построить множество профилей, отличающихся крутизной и кривизной. Вычисляем сначала τ _I , потом τ _II:

x ₀

τ

I 72 ^

d x

а

V  (в—x)2

или

-g ( в - x0 ) - а + >]дв 2 - а

V2 g

4дв2 - а - ^g ( в - x0 ) - а V2 • g

Гипотеза

Может быть, имеет смысл сначала ускорить брусок до большой энергии w и отразить от электрической стенки?

Но, увы, само устройство ускорения обязано также бороться с обратным временем разворота ионов.

Преобразуем выражение

g (в - X0 )2 - а =

xb dx т II =т I +

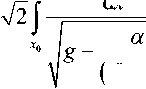
(в - x)2

,

w +

α

( в - X0 )2 .

( в - X 0 ) ²

- а =

α g = w +-------у.

( в - X 0 ) ²

Вычисляя интеграл (118) и учитывая (117), получим

= w ( ^{в -} x 0 ) ² .

Отсюда

V g ( в - X 0 ) ² - а = ( в - X 0 ) V w ,         (121)

^т II =

Vдв2 - а + 7g ( в - х0 ) - а

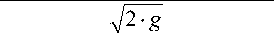
Из выражений (117) и (119) можно сделать несколько парадоксальный вывод: при неограниченном росте энергии w величина g растет, а обе величины τ _I и τ _II , а вместе с ними и их разница, падают к нулю. Иначе говоря, быстрая частица высоко взлетает на стенку и тотчас же с нее сваливается. Этот механизм приводит нас к следующей гипотезе.

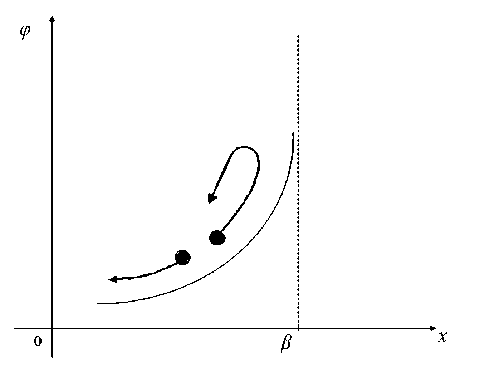
φ

β

x

Рис. 3

. Потенциальный рельеф и время разворота

^т II = 21

4^{g в 2 - а -} ( ^{в -} x 0 ) V w g ^,

4^{g в 2 - а +} ( ^{в - X} 0 ) V w ^g

Опять надо искать min τ _I и max τ _II . Преобразуем (117) к виду

1           ^{в 2 -} ( ^{в - X} 0 )

•

V2 jg ^{в 2 - а} + g ( ^{в - X} 0 ) ^{2 - а}

1         ^{в 2 -} ( ^{в - X} 0 )

—=- • —,      ==---------------.

V2  gв2 - а + Vw (в - X0)

Величина g достигает max при w = в и x ₀ = b ; по крайней мере на первый взгляд из этого следует min τ _I при данных значениях параметров.

Преобразуем и τ _II из (119), получим

т л =

1           ^{в 2 -} ( ^{в - X} 0 )

•

V2    gв ² - а - g ( в - X 0 ) ² - а

^{в 2 -( в - X} 0 ) ______

Vgв 2 - а - Vw ( в - X0 )

Из вида τ _II можно утверждать, что max τ _II достигается при w = в и х ₀ = a . Выражение А т_к = max т II - min т I достаточно громоздкое и не слишком прозрачное. Выбор параметров α и β ,

при которых Δ τ_k минимизируется, представляет отдельную задачу, и ее удобней решить на калькуляторе, задав приемлемые величины a , b , δ . Так или иначе в этом классе найдутся свои оптимумы, но величина Δ w_k вряд ли снизится по сравнению с квадратичном полем.

ЗАКЛЮЧЕНИЕ

Мы рассмотрели ряд полевых структур, пригодных для устройства ортогональных ускорителей и нашли новые возможности управления структурой ионных пакетов в режиме статического электрического питания, но в условиях сильной неоднородности полей. Полностью победить время разворота ионов на этом пути не удается, но существенно снизить его можно, пусть даже ценой некоторого уширения энергетического разброса, с которым можно справиться с помощью подходящего зеркала в схеме масс-рефлектрона. В то же время мы пришли к убеждению, что более успешную компенсацию дефектов ускорителя можно реализовать в пространственно неоднородных нестационарных полях.