Переходные процессы в термосифонах

Замкнутые двухфазные термосифоны за последние десятилетия зарекомендовали себя во многих областях промышленности как высокоэффективные, надежные теплопередающие устройства благодаря сочетанию ряда уникальных свойств: простоты изготовления, отсутствия движущихся частей и потребности в перекачивании теплоносителя, возможности создания изотермических условий на больших площадях и значительной теплопередающей способности [1–9].

Настоящая работа выполнена на медеплавильном комбинате «Святогор» г. Красноуральска на установке для утилизации теплоты отходящих газов за отражательной печью № 2. В отражательную печь загружается шихта, внутри печи поддерживается температура порядка 1500 °С за счет работы газовых горелок. В результате химических реакций выделяются газы с расходом от 75 000 до 94 500 м3/ч. Состав газов: 66,5 % N2; 6,5 % CO2; 16 % H2O; 1,5 % SO2; 9,5 % О2. Для снижения потерь теплоты уходящих газов руководством предприятия было принято решение об установке котла-утилизатора за печью.

Проект котла-утилизатора был разработан ОАО «Уралэнергоцветмет», г. Екатеринбург. Теп-лоутилизатор выполнен с изгибающимся газоходом из-за нехватки места в цехе. Газоход внутри полностью экранирован. В поворотной камере установлен блок термосифонов, который выполняет в большей степени роль заградительного устройства от пыли и шлака, поступающих с газами (рис. 1).

Радиационный газоход

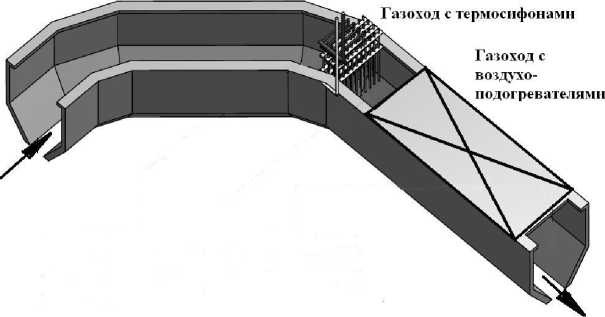
Рис. 1. Схема установки котла утилизатора за печью № 2

Актуальность, научная значимостьс кратким обзором

Термосифон представляет собой наглухо заваренную с обеих сторон трубку, на треть заполненную водой. Часть трубки находится в «горячей» области, где ее омывают газы, вследствие чего вода в термосифоне нагревается, закипает и идет в верхнюю «холодную» часть – конденсатор, представляющий собой теплообменник «труба в трубе», роль охладителя в котором играет вода из барабана сепаратора. Термосифон нагревает ее до температуры насыщения, пар идет на производство. Различным аспектам эксплуатации термосифонов был посвящен ряд работ, ранее опубликованных авторами [10–13].

В настоящее время актуальным направлением для исследований, которое лежит в практической плоскости, является изучение кризисов теп-лопереноса [14–17] в замкнутых двухфазных термосифонах, эксплуатирующихся в различных теплоутилизационных установках на промышленных предприятиях цветной и черной металлургии. Построение математических моделей теп-лопереноса, основанных на замерах фактических параметров работы термосифонов, позволит повысить точность принятия технических решений на этапе проектирования теплоутилизационных установок, а также надежность их промышленной эксплуатации.

Постановка задачи

В данной работе сделана попытка рассмотреть работу термосифона как объекта системы автоматического регулирования с определением основных параметров объекта экспериментальным и расчетным путем. Для этого необходимо получить уравнение объекта. В данном случае это уравнение изменения температуры насыщения в термосифоне во времени в зависимости от режимных и конструктивных параметров термосифона.

Рассмотрим работу отдельного термосифона, осуществляющего передачу теплоты между двумя средами: газом с температурой t г и кипящей водой в барабане котла t б (рис. 2).

Теплота от газов с температурой t г последовательно передается сначала к внешней поверхности испарителя тепловой трубы с t 1 , затем теплопроводностью по стенке к внутренней поверхности, имеющей температуру t ₂. На внутренней поверхности происходит кипение жидкости термосифона, при котором за счет скрытой теплоты парообразования осуществляется передача тепловой энергии кипящей воде с температурой насыщения t _н. В зоне охлаждения теплота от пара за счет его конденсации передается внутренней поверхности трубы участка охлаждения, температура которой t 3 . Затем происходит перенос теплоты к внешней поверхности с t 4 и к нагреваемой среде (кипящей в барабане воде) с температурой t б .

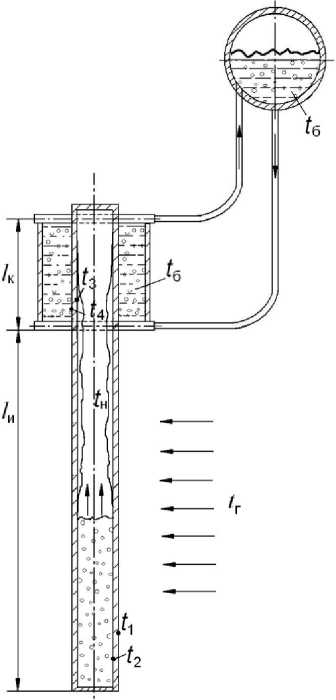
Рис. 2. Схема термосифона: l _и – длина зоны испарения, l _к – длина зоны конденсации

Теоретическая часть

Определим термическое сопротивление каждого элемента в рассмотренной схеме передачи теплоты между двумя средами:

термическое сопротивление теплоотдачи от газов к стенке

R ₁ =     1

πα ₁ l _и d _н

термическое

;

сопротивление теплопроводно- сти в зоне испарения

R= δ ;

• ² πλ l и d н

термическое сопротивление теплоносителя в термосифоне

R ₃ =      1     ;

πα _и l _и d _вн

при испарении

термическое сопротивление при конденсации теплоносителя в термосифоне

R ₄ =            ;

πα _к l _к d _вн

термическое сопротивление теплопроводности в зоне конденсации

R ₅ = δ ; πλ l d кн

термическое сопротивление при теплоотдаче от наружной стенки термосифона к охлаждающему теплоносителю, аналогично (2)

ратуры стенки трубы термосифона в зоне конденса-

„ r            (  24,8

ции пренебрежимо малы

( 237 + 260

• 100 = 5,1 %

R 6 = паи lк d н

.

Передаваемый трубой тепловой поток деляется по формуле

Q - t ' " .

R

Суммарное термическое сопротивление дим по формуле

R - £ R i - R + R 2 + R 3 + R 4 + R 5 + R 6 .

опре-

нахо-

i = 1

При анализе и обработке опытных данных автор работы [18] рекомендует учесть, что коэффи-

циент теплоотдачи при пузырьковом кипении зависит от плотности теплового потока слабее, чем

от температурного напора.

Можно считать, что в термосифонах сравнительно большого диаметра кипение имеет пузырьковый характер. По данным М.А. Михеева [19], для расчета теплоотдачи при пузырьковом кипении воды может быть рекомендована следующая зависимость

a

и

0,18

3, 4 р_s 0,18    q ₂₃

1 - 0,0045 p_s    ’

по сравнению с количеством теплоты, воспринимаемой стенкой трубы термосифона и кипящей водой в зоне испарения.

В первом приближении можно считать, что температура насыщения и температура стенки термосифона в зоне испарения близки. Тогда можно записать в упрощенном виде уравнение для изменения температуры насыщения в термосифоне при изменении температуры газов в котле-утилизаторе

( М м с м + М в с в ) ^ н- = t t - t t . (11) d ^T R ^R к

Здесь R _и и R _к – суммы термических сопротивлений в зоне испарения и конденсации; R и = R 1 + R 2 + R 3 ; R к = R 4 + R 5 + R 6 .

Учитывая, что произведение суммарных термических сопротивлений в зоне испарения и конденсации можно представить как произведение соответствующей поверхности и коэффициентов теплопередачи R _и = k _и F _и, R _к = k _к F _к, уравнение (11) можно представить в виде

( ^М м с м ^{+ М} в с в ) d T =

где р _s, бар; q , Вт/м². Данная формула применима

- k и F u ⁽ t г ^- t н ^)- k к ^F k ⁽ t н ^- t б ) .               ⁽¹²⁾

в диапазоне давлений от 1 до 200 бар.

В начальный момент времени, равный τ = 0, в

При конденсации пара на внутренней поверхности термосифона конденсат выпадает в виде сплошной пленки. Средний коэффициент теплоотдачи в ламинарной области течения рассчитывает-

стационарном состоянии температура насыщения находится из условия dt / d т = 0, откуда определяется начальная температура насыщения

ся по формуле Нуссельта [20]

t = k и ^F u t г,0 ⁺ k к ^F k t б ^н,⁰"    к и F u + к к F k

.

a = 0,943 4 к

gr РжХ Ц ж ^A tl к

где r – удельная теплота парообразования, кДж/кг.

Поскольку значения коэффициентов теплоотдачи как при кипении, так и при испарении зависят от температуры, то после расчета суммарного теплового потока конденсации необходимо уточнять значения всех температур: t ₄ = t ₃ = t_б + QR ₄; t _н = t ₄ + QR ₃; t ₁ = t ₂ = t_г – QR ₄ , ; t _н = t ₁ – QR ₃. При этом температуры насыщения по второму и четвертому выражениям должны совпадать.

Предварительные расчеты показали, что при увеличении температуры газов от 900 до 1000 °С температура стенки в зоне испарения выросла в среднем на 12,5 °С, в зоне конденсации – на 3 °С, а температура насыщения увеличилась на 12 °С. Соответственно, затраты теплоты в различных зонах составили: на нагрев стали в зоне испарения 237 кДж; на нагрев кипящей воды в зоне испарения 260 кДж; на нагрев стали в зоне конденсации 24,8 кДж. Таким образом, при протекании переходных процессов затраты теплоты на изменение темпе-

Пусть далее температура газов скачком изменяется до значения t _г, при этом с течением какого-то времени изменится и температура насыщения t к в термосифоне до конечного значения, равного

t = k и ^F u t г ⁺ k к ^F k t б к     k и ^F u ⁺ k к ^F k

.

Приведем уравнение изменения температуры насыщения в термосифоне к безразмерному виду. Для этого разделим правую и левую часть уравнения на комплекс, равный к _и F _u + к _к F _k . При этом уравнение преобразуется к виду

( ^М м с м ^{+ М} в с в ) dt н

k и F и

k и ^F u ⁺ k к ^F k  d ^т   k и ^F u ⁺ k к ^F k

kF кк kи Fu + kк Fk

⁽ t н ^- t б ) .

( tг - t н )

—

Введем безразмерную температуру 9- 1 _н/ t _б

и безразмерное время, равное a - т

к и F u + к к F< . ^М м с м ^{+ М} в с в .

Разделим правую и левую части уравнения на t _б и, подставив безразмерные комплексы, получим

уравнение для изменения безразмерной темпера-

туры насыщения в следующем виде

= 9 d g

к

-9 ,

где ⁹ к = t к ( б б .

Введя традиционно используемые обозначения при описании свойств объектов автоматического регулирования t _г – t _г,0 = x и t _н – t _н,0 = y , получим уравнение одноемкостного статического объекта в виде

Интегрируя (16) как

J

9 н

d 9

к

-9

g

J d g , получим

Tdy + y = K x . d т         у

решение в следующем виде

9 = 9 к - ( 9 к -9 _H,o ) - exp ( -g ) .              (17)

Здесь постоянная времени представляет собой следующий комплекс, имеющий размерность времени,

T = M м c м ⁺ M в c в к и F u + к к F k ,

Экспериментальная часть

Расчеты изменения температуры насыщения в термосифоне были проведены для блока термосифонов, установленных в конвективном газоходе за металлургической печью на предприятии «Святогор» при следующих условиях: диаметр термосифонов 90 x 6 мм; длина зоны испарения 3,34 м; длина зоны конденсации 1,5 м; начальная температура газа t _г,0 = 900 °С, конечная температура газа t _г,к = 1000 °С. Результаты расчетов представлены на рис. 3, из которого следует, что при ступенчатом изменении температуры газов продолжительность переходного процесса составляет около 10 мин.

В начальный момент времени температура насыщения равна t н,0 и наблюдается равенство подведенного и отведенного количества теплоты:

к и F u ( б г,0 - б н,0 ) - к к F k ( б н,0 - б б ) = 0.        (18)

При резком (ступенчатом) изменении температуры газов от t г,0 до t г температура насыщения в термосифоне возрастает от начальной t н до t . Вычитая из (12) выражение (18), получим

• ( М м с м + М в с в ) ^d 7 ^H■ = k и ^F u ( ^б г ^{- б} н ) ^{- k} K ^F k ( ^б н ^{- б} б ) ^- d т

• ^- k и F 1 ( ^б г,0 ^{- б} н,0 ) ⁺ k к F K ( ^б н,0 ^{- б} б ) = k и F 1 ( ^б г ^{- б} г,0 ) ^-

• ^{- (} k и ^F u ⁺ k к ^F k ) ( ^б н ^{- б} н,0 ) .

а коэффициент усиления равен

Kу

k _и F _и

к и F u + к к F k

.

Рассчитаем постоянную времени для следующих условий: масса трубы М ст = 40,74 кг; масса воды в трубе термосифона М _в = 5,18 кг; теплоемкость воды с _в = 4,19 кДж/(кг·К); теплоемкость стали с _ст = 0,46 кДж/(кг·К); коэффициент теплопередачи от газов к теплоносителю k _и = 50 Вт/(м²·К); коэффициент теплопередачи от теплоносителя к охладителю k _к = 1000 Вт/(м²·К); площадь поверхности теплообмена в зоне испарения F и = 0,87 м²; площадь поверхности теплообмена в зоне конденсации F к = 0,36 м². При этих условиях постоянная времени составляет 100 с, коэффициент усиления равен 0,1.

На самом деле организовать ступенчатое изменение температуры на промышленной печи практически невозможно из-за инерции самой печи и необходимости соблюдения регламента пуска и останова. На рис. 4 приведены: изменение расхода газа при останове печи, изменение температуры газов на выходе из конвективного газохода (КГ) и соответствующее изменение температур насыщения в термосифонах.

Для получения зависимостей изменения температуры газа со временем была получена аппрок-

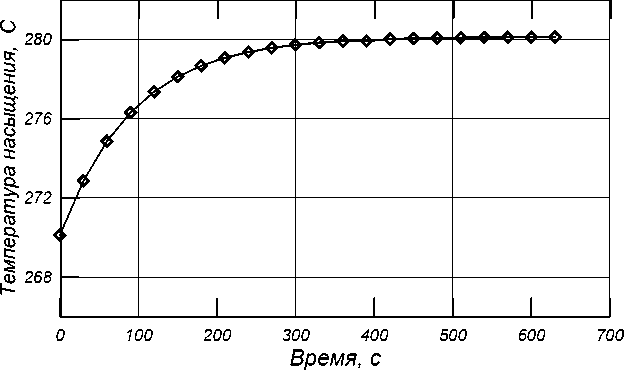
Рис. 3. Изменение температуры насыщения в термосифоне при ступенчатом увеличении температуры газов от 900 до 1000 °С

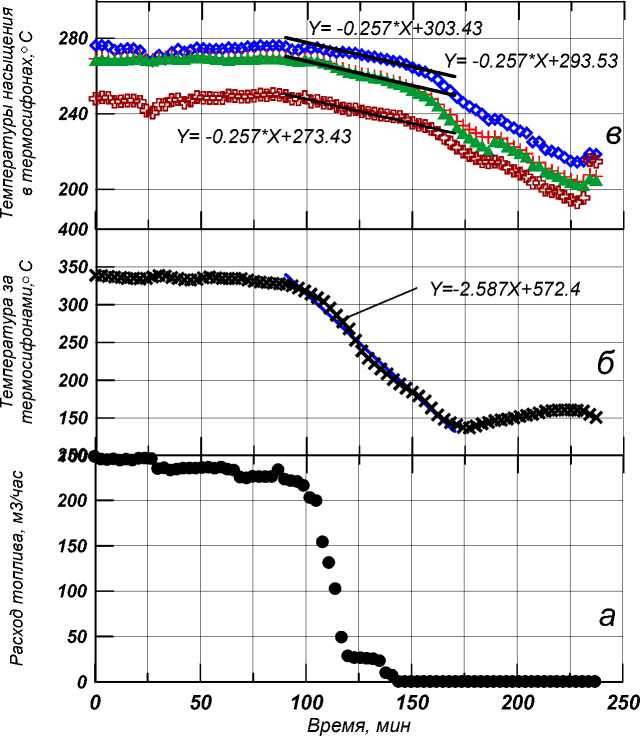
Рис. 4. Изменение расхода топлива ( а ) и температуры на выходе из КГ ( б ) и температуры насыщения в различных термосифонах ( в ) при останове печи

симация на линейном участке изменения температуры газов.

При линейном изменении температуры газов со временем t г = t _г0 - а т уравнение (12) преобра-зутся к виду

• ( М м с м + М в с в ) = d т

• = k и F u ( t г,0 ^{- а Т-} t н ) ^- k к F K ⁽ t н ^- t б ) . ⁽²²⁾

При τ = 0 начальная температура определится из соотношения (13). Далее температура газов изменяется линейно, уменьшаясь до конечного значения t к , которое рассчитывается из выражения (14).

Как и ранее, приведем уравнение изменения температуры насыщения в термосифоне к безразмерному виду, для этого разделим правую и левую часть уравнения (22) на комплекс, равный киFu + ккFk. При этом уравнение преобразуется к виду

( М м с м ⁺ М в с в ) dt н =

• ^к и F u ^{+ к} к ^F k  ^{d т}

• = ^к и F u t г,0 ^{+ к} к F K t б _ t - к и F u а т

• ■  к и F u + к к F k    н к и F u + к к F^

  
  

Как и ранее, введем безразмерную температуру 9 и безразмерное время а. После очевидных преобразований получим уравнения для изменения безразмерной температуры насыщения в следующем виде t/9

__ = 9о -9-фа .                    (24)

d а к„ F„ а М„ с„ + М„ с„

Здесь ф= и-и-- м-м---- в-^.

t б ( к и F u + к к F k ) ²

Для решения данного уравнения находят безразмерный комплекс в виде [21]

и(а) = _0 + ф - фа + С1 exp (-а), где постоянная интегрирования находится из начального условия а = 0, _ = _0. Тогда

и ( а ) = _ ₀ +ф[ 1 -а- exp ( -а ) ] .          (25)

На рис. 4 приведено сопоставление расчетов по (25) с экспериментальными данными. Расчеты изменения температуры насыщения в термосифоне проведены во временном интервале от 90 до 160 мин. Возмущение температурой газов начинается с 90-й минуты, а на 150-й минуте температура газов становится ниже температуры кипения воды в барабане. При этом кипение в термосифоне прекращается и в дальнейшем происходит просто охлаждение термосифона и воды в нем. Как следует из сопоставления линейных аппроксимаций изменения температуры газов (рис. 4б) и изменения температуры насыщения в термосифонах (рис. 4в), тангенс угла наклона линейной аппроксимации переходного процесса для температуры газов составляет 2,57, а для температуры насыщения в термосифоне – 0,257, то есть отличается в 10 раз. Эти данные соответствуют расчетному значению коэффициента усиления, равному 0,1, рассчитанному для параметров существующего термосифона.

Заключение

• 1. Получены расчетные характеристики (постоянные времени и коэффициент усиления) термосифона как объекта регулирования при ступенчатом возмущении изменением температуры газов.

• 2. На величину постоянной времени основное влияние оказывает массовая теплоемкость металла термосифона и воды в нем, а также произведение коэффициентов теплопередачи и площади поверхности в зоне испарения и конденсации.

• 3. Результаты исследования показали совпадение экспериментальных данных с расчетными даже при замене линейного возмущения расхода газов ступенчатым.

Список обозначений

• с м и с в – массовые теплоемкости металла и воды, кДж/(кг·К);

• d _вн и d _н – внутренний и наружный диаметры трубы, м;

F _и, F _к – площади поверхности теплообмена в зонах испарения и конденсации, м²;

• k _и, k _к – коэффициенты теплопередачи в зонах испарения и конденсации, Вт/(м²·К);

• l к , l и – длина зон конденсации и испарения, м;

М м и М в – массы металла стенки трубы термосифона в зоне испарения и воды в термосифоне, кг;

• r – удельная теплота парообразования, кДж/кг;

• t _н, t _г, t _б – температуры: насыщения, газов, теплоносителя в барабане котла, °С;

• α 1 – коэффициент теплоотдачи от газов к стенке, (определяется из расчета КУ), Вт/(м² ⋅ К);

• α и – коэффициент теплоотдачи от стенки к кипящей жидкости (при испарении), Вт/(м² ⋅ К);

• α к – коэффициент теплоотдачи при конденсации на вертикальной трубе, Вт/(м² ⋅ К);

• δ – толщина стенки термосифона, м;

• λ – коэффициент теплопроводности стали, Вт/(м·К);

• τ – время, с.