Перекачка токсичной смеси газов в технологических процессах

Одна из особенностей оборудования химических производств заключается в том, что технологические процессы в них нередко протекают при высоких (или низких) температурах и давлениях; рабочие среды могут быть токсичными и обладать повышенной коррозионной активностью [1]. Чтобы обеспечить безопасность

EDN UJCIFV

1Великанов Николай Леонидович – доктор технических наук, профессор, профессор НОЦ судостроения, морской инфраструктуры и техникител. 8 (4012) 56 48 02; e-mail: , ;

2Наумов Владимир Аркадьевич – доктор технических наук, профессор, профессор кафедры техносферной безопасности и природообустройства, КГТУ, тел. 8 (4012) 99 53 37; e-mail: ,

эксплуатации такого оборудования, эффективность и долговечность, при его проектировании необходимо принять ряд специфических конструктивных решений [2-6].

Ряд сложных технологий с использованием токсичных газов используется в нефтедобывающей промышленности [2-4]. Такие процессы требуют специальных трубопроводов [5].

В [6] для подачи концентрированной серной кислоты используется специальная вакуумная установка, которая позволяет избежать контакта агрессивной жидкости с деталями насоса.

В данной статье рассматривается случай применения токсичной смеси газов, которую необходимо медленно сжать и подать в зону технологического процесса. В этом случае может быть использована схема, показанная на рис. 1. На предварительном этапе поршень 5 находится в крайнем левом положении, вентили 3 и 8 закрыты, после открытия вентиля 7 в цилиндрическую рабочую камеру (ЦРК) поступает смесь газов специального состава с давлением, незначительно превышающим атмосферное P A . На рабочем этапе вентили 7 и 8 закрыты, вентиль 3 открыт; шестеренный насос (ШН) 2 подает рабочую жидкость в ЦРК-4. Поршень 5 начинает двигаться вправо, поэтому давление в ЦРК-6 возрастает. Когда давления достигнет критической величины P K , насос прекращает работу, вентиль 3 закрывается. На завершающем этапе открывается вентиль 8, смесь газов подается по транспортному трубопроводу в зону технологического процесса. Затем весь цикл повторяется. На внутренней поверхности ЦРК и поршня имеется специальное защитное покрытие.

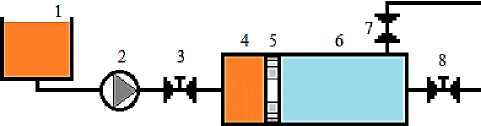
Рисунок 1 - Принципиальная схема установки: 1 - емкость с рабочей жидкостью,

2 - шестеренный насос, 3, 7, 8 - запорные вентили, 4 - часть ЦРК с РЖ, 5 - поршень, 6 - часть ЦРК с газом

Для формирования математической модели примем следующие допущения:

• 1.    Рабочая камера герметичная и теплоизолированная.

• 2.    Силой трения поршня и сжимаемостью РЖ можно пренебречь.

• 3.    Газ считаем совершенным с показателем адиабаты у.

• 4.    Производительность ШН невелика, сжатие газа происходит настолько медленно, что этот процесс можно считать квазиравновесным.

• 5.    Гидравлическим сопротивлением подводящего трубопровода можно пренебречь.

Для моделирования рабочих характеристик насоса используем данные испытаний НМШФ 0,6-25-0,25/25 [7], проведенных на минеральном масле с кинематической вязкостью 75 сСт при частоте вращения ведущей шестерни 980 об/мин. При перепаде давления 2,5 МПа этот насос предназначен для подачи жидкостей с вязкостью от 36 до 2250 сСт. Нижний предел вязкости ограничивается смазывающей способностью перекачиваемой жидкости, верхний -мощностью электродвигателя и всасывающей способностью насоса.

На рис. 2 результаты испытаний показаны точками. Видно, что зависимость подачи и затраченной мощности от перепада давления у шестеренного насоса близка к линейным функциям, как в [8]:

Q = F 1 (р ) = Q 0 ^(1 - a- p ), N = F 2 (p ) = N y(1 + Р’ p ),

(1) где p = A P / P a = ( P - P a )/ P a - безразмерный перепад давления (БПД);

P - давление в ЦРК, МПа;

P a - атмосферное давление, МПа;

Q о - подача ШН при p =0, дм³/мин;

N 0 - затраченная мощность ШН при p =0, кВт;

• а, в - безразмерные эмпирические коэффициенты. Их значения, найденные для НМШФ 0,6-25-0.25/25 методом наименьших квадратов равны: a=0,0041;

в=0,0403; Q о = 4,717 дм³/мин;

N о = 0,249 кВт.

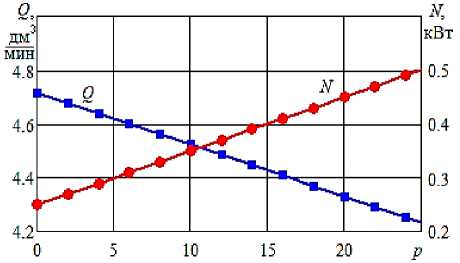
Рисунок 2 - Зависимость подачи и затраченной мощности от БПД шестеренного насоса НМШФ 0,6-25-0.25/25. Точки - экспериментальные данные [7], линии - расчет по (1)

Заметим, что коэффициент β почти в 10 раз больше коэффициента a.

Кроме подачи и затраченной мощности, в [7] приведена зависимость гидравлического коэффициента полезного действия (ГКПД) от перепада давления (точки на рис. 3). Для оценки энергетической эффективности насосов используют ГКПД η и показатель удельных энергетических затрат (ПУЭЗ) E, которые рассчитываются по формулам (2) [9, 10]:

П = 100- P • Q/N = 100' P a ' p • F 1 ( p )/ F 2 (p ),

E = F 2 (p )/ F i (p ).              (2)

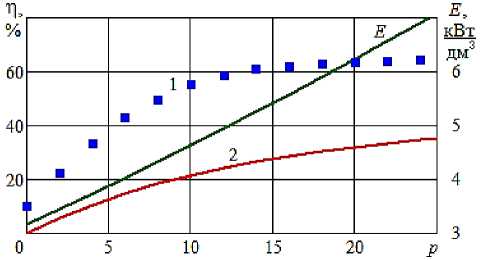
Рисунок 3 - Зависимость гидравлического КПД (1 и 2) и ПУЭЗ от БПД шестеренного насоса НмШф 0,6-25-0.25/25; 1 - экспериментальные данные КПД [7], линии - расчет по (2)

На рис. 3 ГКПД (линия 2) рассчитан по первой формуле (2). Точки из [7], представляют собой косвенные измерения, т.е. должны быть рассчитаны по той же формуле с использованием значений Q и N на рис. 2. Откуда точки на рис. 3 должны лежать на линии 2. Но они показывают значения почти в два раза большие, чем линия 2. Кроме того, при p =0 точка находится на уровне η=10 %, а не η=0, как должно быть в соответствии с физическим смыслом ГКПД. Скорее всего, такая разница связана с погрешностями оформления технической документации.

Заметим, и ГКПД, и ПУЭЗ являются монотонно возрастающими функциями БПД. Но увеличение ГКПД говорит об улучшении энергетической эффективности, а увеличение ПУЭЗ - о ее ухудшении. Как в [9, 10], для оценки энергетической эффективности ШН следует пользоваться ПУЭЗ.

Сначала рассмотрим случай, когда поршень обладает идеальной теплопроводностью, и процесс сжатия газа можно полагать изотермическим. Незначительным изменением температуры РЖ пренебрегаем. Тогда

P•V = P 0 - V 0 = const,          (3)

где   P0 = Pa - давление в ЦРК в начале рабо чего этапа, МПа; V0 = S-L - объем ЦРК, м;

S - площадь поперечного сечения ЦРК, м²;

L - длина ЦРК (за вычетом толщины поршня), м.

Обозначим через X длину части ЦРК, занятой РЖ, x = X¹L . Тогда из (3) следует:

P = PA•L/(L - X) = Pa/(1 - x), x < 1.(4)

Из (4) получим выражение для БПД:

p = P/Pa-- 1 = 1/(1 - x) - 1.(5)

Дифференциальное уравнение притока массы РЖ m в ЦРК имеет вид:

= G, т(0) = 0,(6)

dt где G - массовый расход РЖ, который обеспечивает ШН. Если гидравлическим сопротивлением трубопровода и сжимаемостью РЖ можно пренебречь, то

G = Р' Q = Р' F1(p ), m = Р' S'X ,, где р - плотность РЖ, кг/м³.

Подставив (7) в (6), получим dY

S • — = ^( Р), x (0) = 0, dt где t - время с начала рабочего этапа, мин.

Выразим БПД в первой формуле (1) рез x по (5):

F1(p ) = Q о '[1 - а'(1/(1 - x ) - 1)].

че-

Введем безразмерное время т = tQ о / V о . Тогда задача Коши (8) может быть записана в следующей безразмерной форме

— = 1 -а-Г(1 - x )-1 -11, x (0) = 0,(10)

d т

В дифференциальном уравнении (10) переменные можно разделить:

т = Ф ⁽ x ) = x --^а—у • In [ 1 ^{- (}1 + ^{а )} • x ] . 1 + а (1 + а )

Рассмотрим другие условия: поршень обладает идеальной тепловой изолированностью, сжатие газа полагаем адиабатическим. В отличие от (5) выражение для БПД будет таким: p = 1/(1 - x )^-Y - 1.          (13)

Безразмерная форма задачи Коши будет отличаться от (10) только показателем степени

Y:

dx = 1 -аТ (1 - x Г- 1 1 , x (0) = 0 , (14)

d т

Разделение переменных и интегрирование дифференциального уравнения (14) приво- дит к такому выражению:

т = I d -------- ,.   (15)

0 1 -а-[ (1 -- ) -’ - 1 ]

Интеграл в (15) не имеет первообразной в элементарных функциях, поэтому он рассчитывался численным методом.

На рис. 4 показана рассчитанная зависимость БПД от x (частью ЦРК, занимаемой РЖ). В изотермическом процессе предельное давление (2,5 МПа) достигается при x1=0,962, а в адиабатическом процессе раньше – при x2=0,902. В реальном процессе будет промежуточное значение x2 < x < x1.

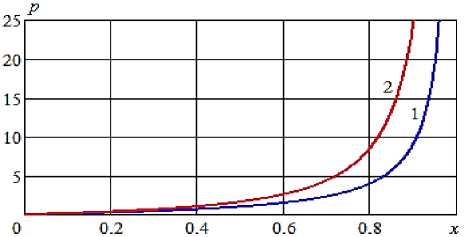
Рисунок4 – Связь между БПД и частью ЦРК, занимаемой РЖ: 1 – изотермический процесс, 2 – адиабатический процесс

На рис. 5 показано, как возрастет время достижения предельного давления при увеличении коэффициента α нагрузочной характеристики ШН. При α=0,0041 безразмерное время τ 1 =0,915; τ 2 =0,961 при α=0,0164; τ 3 =1,003 при α=0,0246.

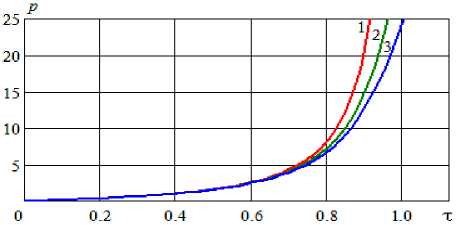
Рисунок 5 – Динамика БПД в адиабатическом процессе при разных уклонах нагрузочной характеристики ШН: 1 – α=0,0041; 2 – α=0,0164; 3 – α=0,0246

Рассчитаем величину механической работы, затраченной ШН на перекачивание РЖ, учитывая равенства t = Φ( x ) = φ( x )∙ V 0 /Q 0 , dt = Φʹ( x )∙ dx :

t 1 ^x 1

A = j N ( t ) dt = j F ₂ [ Ф ( x ) ] • Ф' ( x ) dx . (16)

0 0

Механическая работа, затраченная ШН за один цикл на перекачивание РЖ при изотермическом процессе, по формуле (16) равна A = 338,4 кДж. Аналогичным образом рассчитанная работа при адиабатическом процессе меньше, A = 328,7 кДж.

Выводы