Перекрытие спектра однопериодного терагерцового импульса, уширяемого в нелинейной среде из-за фазовой самомодуляции, и спектра излучения, генерируемого в его поле на утроенных частотах

Терагерцовое (ТГц) излучение впервые экспериментально было получено почти 100 лет назад советской ученой А.А. Глаголевой–Аркадьевой [1]. Полезно отметить, что ТГц излучение, находясь на пересечении оптического и радиодиапазонов, обладает особенностями обеих областей спектров электромагнитного излучения. Важной отличительной чертой большинства нынешних источников импульсного ТГц излучения является то, что они генерируют импульсы, состоящие всего из нескольких колебаний электрического поля. В том числе возможна генерация ТГц импульсов, которые представляют собой лишь одно полное колебание поля излучения [2]. Такие предельно короткие по числу колебаний ТГц импульсы называют однопериодными. Методы генерации импульсного ТГц излучения основаны, как правило, на различных нелинейных эффектах [3–7]. Развитие этих методов в последние годы привело к созданию источников ТГц импульсов высокой интенсивности. Например, в органических кристаллах методом оптического выпрямления фемтосекундных импульсов ближнего ИК диапазона спектра были сгенерированы ТГц импульсы с интенсивностью более 10 ТВт/см2 [8], а в источниках, основанных на оптическом пробое, – порядка 8 ТВт/см2 [9]. Достижение таких высоких интенсивностей у ТГц импульсов открыло возможности для развития нелинейной оптики ТГц излучения [10– 14]. Пионерские работы в этой области показали как теоретически, так и экспериментально, что нелинейный показатель преломления материалов в ТГц-спектральном диапазоне может превосходить для одних и тех же сред значения для видимого и ближнего ИК диапазонов на несколько порядков [15– 17]. Помимо высоких значений, нели-нейнность в этом диапазоне обладает малой инерционностью [18, 19], что является многообещающим критерием для устройств нелинейной ТГц фотоники.

К настоящему времени было показано, что нелинейные явления в средах при взаимодействии с веществом высокоинтенсивного импульсного ТГц излучения обладают рядом особенностей. Например, для волн из малого числа колебаний явление самофокусировки может не наблюдаться даже в том случае, когда интенсивность излучения превышает пороговое значение самофокусировки во много раз [20]. В поле однопериодных ТГц импульсов могут значительно изменяться такие классические явления нелинейной оптики, как генерация второй и третьей гармоник [21 – 23]. В работе [22] теоретически было показано, что в случае ТГц импульса, который состоит только из одного полного колебания электрического поля, возникающая в нелинейной среде единая сверхуширенная спектральная структура формируется за счёт перекрытия спектра излучения, генерируемого на утроенных частотах, и спектра на основных частотах импульса, уширяемого из-за фазовой самомодуляции излучения. Интерференционный минимум этой структуры может оказаться на третьей гармонике по отношению к центральной частоте входного импульса, а максимум – на её четвертой гармонике. В работе [24] указанный эффект был продемонстрирован экспериментально.

В настоящей работе теоретически исследуются особенности перекрытия спектра однопериодного импульса, уширяемого в нелинейной среде из-за фазовой само-модуляции, и спектра генерируемого излучения на утроенных частотах. Показано, что модуль степени такого перекрытия для однопериодного импульса составляет | s |=0,85. Комплексные спектры сдвинуты по фазе на π , что взаимно ослабляет эти нелинейные эффекты. Коэффициент ослабления для однопериодного импульса составляет k = 7,7. Наблюдаемый в экспериментах сдвиг максимума спектра, генерируемого в нелинейной среде в поле однопериодных импульсов высокочастотного излучения на учетверённые частоты объяснён неоднородностью по частоте взаимного ослабления нелинейных эффектов.

Уравнение динамики поля и его нормировка

Параксиальное распространение линейно поляризованного импульсного ТГц излучения в изотропной нелинейной среде может быть описано с помощью полевого уравнения [25, 26]:

∂ E ₊ N 0 _⋅ ∂ E ∂ zc ∂ t

∂ ³ E        ∂ E    c t

-a+gE2 =∆Edt′, (1) ∂t3     2 ∂t 2N0 ⊥∫-∞ где E – напряжённость электрического поля, z – координата, вдоль которой происходит распространение излучения, c – скорость света в вакууме, N0 и a – эмпирические постоянные, описывающие зависимость линейного показателя n преломления от частоты ω в виде n(ω) = N0 + caω2,

∂ ² ∂ ²

∆_⊥ =    +

∂ x ² ∂ y ²

поперечный лапласиан, x и y – поперечные направлению распространения излучения координаты, g 2 =2 n ²/ c – коэффициент, характеризующий кубическую нелинейность среды, n 2 – её коэффициент нелинейного показателя преломления.

Для теоретического анализа и нахождения решений уравнение (1) удобно нормировать, используя безразмерные переменные [24]:

E ( z , t )       zN 0       t

E ( z , t )=        , z = , t = , x = x / r 0 , y = y / r 0 ,

E 0 c τ 0 τ 0

где E 0 – амплитуда ТГц импульса, τ 0 – характерное время нарастания поля импульса от нуля до максимума, r 0 – поперечный размер пучка. Тогда в новых переменных уравнение (1) примет следующий вид:

∂ E ∂ E + d z d t

^d2E 2 5 E-. x

^- µ disp     ⁺µ nl E     ⁼ µ diffr ∆ ⊥

∂t3

t

Edt', (2)

-∞

где ca             c2τ20

µdisp =,µdiffr =       ,µnl =,

N 0 τ 0 ²          2 N 0 ² r 0 ² N 0

Δ⊥ =∂x +∂,∆nnl =1 n2E02(СГС) =n2′I(СИ), ∂x2 ∂y22

n 2 ( СГС ) = cN 0 /(40 π ) n 2 ′ ( СИ ) ,

I – интенсивность ТГц импульса.

При использованной выше нормировке переменных значения производных и интеграла по времени в уравнении (2), по крайней мере на начальном этапе описания распространения импульса, имеют порядок единицы. Поэтому доминирование в эволюции полевой структуры импульса явлений дисперсии, дифракции или нелинейной рефракции определяется величиной коэффициентов µ disp , µ diffr и µ nl .

В настоящей работе рассмотрим случай, когда µ nl >>  µ disp, µ diffr , т.е. когда дифракция и дисперсия оказывают на эволюцию поля импульса значительно меньшее влияние, чем нелинейность среды, и ими можно пренебречь. Рассмотрим, когда такое приближение возможно, для следующих сред: этанола (C 2 H 6 O), кристалла кремния (Si) и кристалла ниобата лития (LiNbO 3 ). Выбор именно этих сред обусловлен их большим коэффициентом нелинейного показателя преломления n' ₂ в ТГц-диапазоне частот: 6^10 ^–9 см²/ Вт [17], 3,5^10 ^–12 см²/ Вт [28] и 7^10 ^–11 см²/ Вт [16] соответственно.

Параметры, описывающие дисперсию показателя преломления в ТГц дипазоне, имеют значения: для этанола N 0 = 1,7, a = –8^10^–36 с³/ м [29], для кремния N 0 =3,2, a = 1,4^10^–35 с³/ м [30] и для ниобата лития N 0 = 5,12, a = 4,47^10^–36 с³/ м [31]. Характерное время изменения поля импульса в ТГц диапазоне составляет τ 0 = 1 пс. Радиус пучка при проведении оценок будем полагать равным r 0 =10 λ , где λ =0,3 мм – длина волны ТГц импульса. Расcчитанные величины µ disp и µ diffr при этих параметрах материалов и излучения приведены в табл. 1. Там же указаны значения интенсивности излучения, при которых µ nl значительно превосходит µ disp и µ diffr . Все эти значения достижимы в лабораторных условиях.

Табл. 1. Значения коэффициентов, характеризующих вклад в эволюцию поля импульса в разных средах дисперсии, дифракции и нелинейной рефракции

Среда	| P dsp |	Ц diffr	Ц nl
C 2 H 6 O	1,4^10–3	1,7^10–3	1,4-10 -2 (для I - 10 6 Вт/см2)
Si	1,3^10–3	4,9^10–4	4,4-10 -3 (для I - 10 9 Вт/см2)
LiNbO 3	2,6^10–4	1,9^10–4	5,5-10-3 (для I - 10 8 Вт/ см2)

Из табл. 1 видно, что для всех трех сред ц nl >>  Ц disp, Ц diffr , т.е. дифракция и дисперсия оказывают на эволюцию поля импульса значительно меньшее влияние, чем нелинейность среды. Таким образом, ими можно пренебречь, и уравнение (2) записать в виде:

Г     Г

Г

д E д E д E _л — + ^ + Ц ni E 2^ = 0- д z д t д t

В данном уравнении поле E зависит от поперечных координаты % и у лишь параметрически, поскольку явлением дифракции по заданным условиям можно пренебречь. Это означает, что на границе нелинейной среды поле в рассматриваемой задаче, которая описывается уравнением (3), по-прежнему может зависеть от поперечной координаты E = E ( x , y , z , t ), например, иметь Гауссово поперечное распределение. Тогда в центре пучка, где поле на границе среды больше, его изменения в нелинейной среде в соответствии с нелинейным уравнением (3) будут сильнее. На периферии пучка – меньше. Но в приближении математической модели (3) изменение формы поля с расстоянием z рассчитывается для полей с различными координатами х и y независимо.

Решение уравнения динамики поля методом последовательных приближений

Общее решение уравнения (3) можно найти итерационным методом, поскольку, как выше было показано, при рассмотренных значениях интенсивности излучения выполняется неравенство ц _nl <<1. Таким образом, решение (3) может быть представлено в виде разложения в ряд по малому параметру:

E ( z, t ) = E ⁽⁰⁾( z,t ) + Ц _nlE ⁽¹⁾( z, t ) + Ц 2 Е ⁽²⁾( z, t ) + ..., (4)

где т = t - z - безразмерное время в бегущей системе координат [21], вид E ( ⁰⁾( T ) определяется по форме поля импульса E ( Г ) на границе нелинейной среды (при z = 0).

Используя общее решение (4, 6), рассмотрим динамику поля в среде с кубической нелинейностью одного из самых удивительных объектов ТГц оптики – однопериодного импульса. Такие предельно короткие по числу колебаний ТГц волны получают, например, при выпрямлении фемтосекундных импульсов ближнего ИК диапазона спектра в средах с квадратичной нелинейностью [32]. Их математическую модель можно представить в виде [33]:

E ( t ) = E ₀ ^t exp Т 0

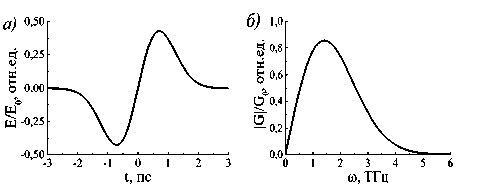
Вид импульса (7) для значения длительности импульса т ₀= 1 пс представлен на рис. 1 а .

Спектральная плотность

да

G ( to ) =    E ( t ) ■ exp( - i to t ) dt

-да

поля импульса (7) имеет вид

G ( to ) = - iG₀ toT ₀ exp

toT 0

где G ₀ =(л/лт₀ /2) E ₀. Вид модуля спектра импульса

где E ^{( i )} – i -е приближение, ниже мы ограничимся только первыми двумя слагаемыми. Соответственно, решение нелинейного уравнения (3) сводится к решению системы двух линейных уравнений:

(8) представлен на рис. 1 б .

д E д E ⁽⁰⁾ _л

"IT+^T ~ ’ д^+(E (0))2 -. дz д t д t

=0.

Решение системы (5) имеет вид:

E ⁽⁰⁾( т , z ) = E ⁽⁰⁾( т ),

E ⁽¹⁾( т , z) = - E ⁽⁰⁾² E^z, дт

Рис. 1. Зависимость нормированного поля E однопериодного ТГц импульса от времени t (а) и модуля его спектральной плотности |G| от частоты to (б)

Из рис. 1 видно, что импульс (7) является нечётной функцией и представляет собой лишь одно полное колебание поля излучения. Значения максимума и минимума поля импульса составляют ±(E0141ё). Временной промежуток между наблюдением минимального и максимального значений поля составляет V2т0. Спектр однопериодного импульса широк. Максимум модуля его спектральной плотности находится на частоте to = V2 /тп     и составляет max

V2exp( - 1/ 2) G ° . Величина отношения модулей спектральных плотностей на частоте to max и утроенной по отношению к ней частоте 3 ® max согласно выражению (8) составляет 1/3(exp(4)).

После нормировки, которая представлена выше, поле импульса примет безразмерный вид:

E ( t ) = t exp( - 1 ²),                                  (9)

а его спектр (8):

G ( to ) = - iG ° to exp( -to ² / 4).                       (10)

где G ° = Vn /2 , to = toT ° .

При граничном условии вида однопериодной волны (9) (при z = ° ) общее решение (4, 6) в спектральной форме принимает вид:

G = G ^(o) (65) + ц ni ( G^ (65, z ) + G Z (cd , z )),        (11)

G ^(o)( to ) = - iG ° to exp( -to ² / 4) ■ exp( - i 65 z ),          (12)

J п         ^ to ² b

G$_g (co , z ) = 648^3 ■^{ю 4} exp |- 32 J ■ z ■ exp( - i to z ), (13)

a 2

G SM ( to , z ) = - 36-/= ■ to ² exp I - 12 I ■ z ■ exp( - i to z ), (14)

а в полевой форме:

El = E(o) (t) + цni (E^ (t, z) + ESPm (t, z)),(15)

E (0)(t) = t exp(-T2),(16)

E^ (t, z) = ' ■ (12t4 - 12t2 +1) ■ exp(-3T2)z,(17)

ESPm (t, z) = 1 ■ (6t2-1)exp(-3T2) z.(18)

В выражениях (11– 14) и (15– 18) E ⁽⁰⁾ и G ⁽⁰⁾ описывают динамику поля импульса и его спектра в оптической среде при малой интенсивности излучения, когда нелинейность среды не проявляется. E_T ⁽¹ _F ⁾ _G и G_T ⁽¹ _F ⁾ _G описывают изменения в структуре поля и его спектра, обусловленные генерацией излучения на утроенных частотах (ГУЧ), а E_S ⁽¹ _P ⁾ _M и G_S ⁽¹ _P ⁾ _M – фазовой самомодуляцией импульса (ФСМ). Их нелинейный вклад в общую динамику поля E и его спектра G характеризуется величиной коэффициента ц nl .

Отметим, что в статьях [21, 22] утверждается неразделимость эффектов уширения спектра однопериодной волны из-за ГУЧ и ФСМ. В настоящей статье мы показываем, что в теории эти эффекты, на наш взгляд, различимы. Как видно из формулы (13), фаза изменения спектра ТГц волны, обусловленная ГУЧ, опережает фазу спектра основной части волны (12) на п /2, а фазу изменений, вызванных ФСМ (14), - на п .

Покажем, что именно такие фазовые сдвиги характерны между спектрами излучения утроенных частот и волны, фаза которой модулируется за счет явления самовоздействия, на примере гармонического граничного условия

E = E ° sin( to 1 ) = - i 2 E ° e ^{to 1} + c . c .,                  (19)

вид которого после нормировки представляется как

i

I L = - ^ e“ + c . c .                                   (20)

Выбор гармонического излучения в виде синусоидальной (а не косинусоидальной) волны обусловлен тем, что такая форма волны представляется четной функцией, как и ее однопериодная часть (9).

В (19), (20) c.c. означает комплексное сопряжение. Решение (4, 6) для такого граничного условия принимает вид

E = E(o) (t) + цni (ETFg (t, z) + E^M (t, z)),(21)

1 - • п

E(o) (t) = 2 e '2 ■ eit + c.c.,(22)

E(1)g(t, z) = 2e-i-° ■ e3it^ z + c.c.,(23)

ESPM (t, z ) = 2 e -■ e^ z + c.c.(24)

Как видно из наглядного решения для монохроматического излучения на входе в оптическую среду (19), однопериодной вариацией которого является волна (7), фаза генерируемой в нелинейной среде третьей гармоники (23) опережает фазу волны на основной частоте (22) на п /2, а нелинейный сдвиг фазы на основной частоте (24) - на п .

Такие же отличия в фазе спектральной плотности основной части импульса (16), её изменений из-за нелинейных эффектов ГУЧ (17) и ФСМ (18), с учётом того, что -1 = exp ( i п ), имеем и в решении для однопериодной волны (15). Но в отличие от случая монохроматических волн (21 – 24), для которых спектры излучения на основной и на утроенных частотах значительно разнесены, для однопериодной волны (11) с исходно очень широким спектром его изменения в нелинейной среде, связанные с эффектами ГУЧ и ФСМ, перекрываются.

В заключении настоящего параграфа отметим, что указанные выше изменения в фазе спектра излучения, вносимые ГУЧ и ФСМ, имеют место только для рассмотренных выше четных по форме синусоидальной (гармонической) волны и ее однопериодной части. Но, можно показать, что, например, для нечетной по форме косинусоидальной (тоже гармонической) волны и ее полуторапериодной части это будет уже не так. Хотя для полуторапериодного импульса также будет наблюдаться перекрытие его спектра, уширяемого в нелинейной среде из-за фазовой самомодуляции, и спектра излучения, генерируемого в поле этого импульса на утроенных частотах. Т.е. задача разделения вкладов ГУЧ и ФСМ в общее уширение спектра импульсов из малого числа колебаний разной формы в нелинейной среде требует еще дополнительного изучения.

Интерференция спектра однопериодной волны, уширяемого из-за ФСМ, и спектра излучения, вызванного ГУЧ

На рис. 2 приведён вид изменений безразмерных величин поля и вещественной амплитуды спектра однопериодной волны (9) из-за ГУЧ E_T ⁽¹ _F ⁾ _G , G_T ⁽¹ _F ⁾ _G (13, 17) и из-за ФСМ E_S ⁽¹ _P ⁾ _M , G_S ⁽¹ _P ⁾ _M (14, 18). Численные значения этих изменений на рисунке даны для ц nl ■ z = 1. При отображении вещественной амплитуды комплексного спектра G S (1 P ) M учли, что exp( i π )=–1. Под вещественными амплитудами спектров понимаем G tfg = G , ■ exp( i «> z) и G spm = G SPM ■ exp( i & z) •

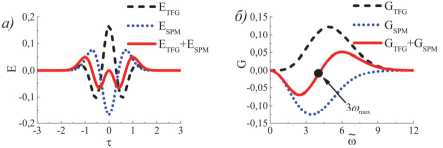
Рис. 2. Зависимость изменений безразмерных величин поля однопериодного импульса E от безразмерного времени в бегущей системе координат τ (а) и вещественной амплитуды его спектра от нормированной частоты ю (б) из-за ГУЧ (пунктирная линия) и ФСМ (линия точками). Сплошная линия описывает результат интерференции ГУЧ и ФСМ

Из рис. 2 а видно, что вклады в поле однопериодной волны, вызванные эффектами ГУЧ и ФСМ, находятся в противофазе и близки по амплитуде, т.е. эти нелинейные эффекты ослабляют друг друга. Особенно отчётливо видно это из рис. 2 б . Вклады ГУЧ и ФСМ в спектр значительно перекрываются и имеют разные знаки. Результирующее изменение спектра однопериодного импульса в нелинейной среде значительно слабее каждого из этих вкладов. Охарактеризуем эти выводы количественно.

Степень перекрытия вкладов ГУЧ и ФСМ в спектр излучения s=

∞ G TFG -∞

^⋅ G SPM d ^ω

∞

∞∞ G TFG d ^ω⋅   G SPM

-∞           -∞

d ω

для однопериодной волны в нелинейной среде (15– 18) составляет s = - 57 ≈- 0,85, т.е. она недалека от максимального значения, равного –1. Отрицательная величина s показывает, что эффекты ГУЧ и ФСМ при интерференции ослабляют друг друга. Обратим внимание на то, что представленный коэффициент не зависит от величины µ nl , поскольку динамика обоих рассматриваемых нелинейных процессов определяется одним и тем же µ nl . Также отметим, что, как следует из формул (17) и (18), он не зависит и от z .

Коэффициент ослабления изменений спектров, обусловленных ГУЧ и ФСМ

∞

G T ² FG d ω k = ^-∞                ,

∞

( G TFG ⁺ G SPM ) + d ^ω -∞

где ( G TFG + G SPM ) + – только положительные значения суммы вещественных амплитуд спектров, для однопериодной волны (12) в нелинейной среде составляет

35e3 3π k=

270 + 11 e ³ 3 π ⋅ erfc( 3)

≈ 7,7,

где erfc( z ) = 1 – erf( z ). Как видно из формулы (26), коэффициент ослабления определяется отношением энергии излучения, генерируемого на утроенных частотах в случае гипотетического отсутствия ФСМ, к энергии излучения на утроенных частотах, остающегося после интерференционного ослабления его за счет ФСМ. Таким образом, интерференция ГУЧ и ФСМ приводит к значительному общему ослаблению эффекта ГУЧ.

Из соотношений (15–18) следует и из рис. 2 б видно, что максимальным значениям спектральной плотности ГУЧ и ФСМ соответствуют нормирован- max _T , _FG =2^6 и й max _SPM =2ч3 . Полное (до нуля) интерференционное гашение эффектов ГУЧ и ФСМ наблюдается на нормированной частоте й = 3-72 . Этот факт интересен тем, что данная величина в точности соответствует значению утроенной по отношению к частоте максимума спектральной плотности однопериодного импульса нормированной частоты 3 й _max , где й _max = to _max ■ т ₀. Исчезновение генерации излучения третьей гармоники по отношению к частоте максимума исходного спектра и сдвиг максимума генерируемого в нелинейной среде контура частот излучения на частоту 3л/2 й max иллюстрировано на рис. 3. На этом рисунке приведён модуль суммарного спектра (11) однопериодной волны в нелинейной среде. Спектр иллюстрирован для значений ц nl ■ z = 1 (близко к реализованному в эксперименте [24]). Из рисунка видно, что при частоте 3 й _max излучение полностью не исчезает. Это связано с тем, что при полном интерференционном гашении на этой частоте ГУЧ и ФСМ ненулевым на ней является широкополосное излучение основной части импульса, которое сдвинуто по фазе колебаний по отношению к нелинейным эффектам на π /2. Как выше было отмечено, отношение значения модуля спектральной плотности однопериодного импульса частоты 3 й _max к его максимальнмоу значению равно 3exp(–4). Это означает, что появление в нелинейной среде спектрального контура на учетверённых частотах носит пороговый характер и наблюдается при ц nl ■ z >0,81. Данное пороговое значение вытекает из требования глубины провала в спектре излучения на частоте 3(b _max в 20% от высоты максимума на частоте 3д/2(О max . Во вставке на рис. 3 дано искажение формы поля импульса в нелинейной среде.

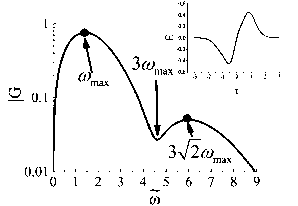
Рис. 3. Зависимость нормированного модуля спектра G однопериодного импульса в нелинейной среде от нормированной частоты to при цnl • z = 1. На вставке приведена зависимость в нелинейной среде нормированного поля E от безразмерного времени в бегущей системе координат τ

Заключение

В настоящей работе изучены особенности интерференции вкладов в спектр однопериодного ТГц импульса, распространяющегося в среде с кубической нелинейностью, явлений ГУЧ и ФСМ. Показано, что степень перекрытия генерируемых в нелинейной среде компонент спектра однопериодного импульса из-за ГУЧ и ФСМ составляет s =–0,85. Отрицательное значение этой величины означает, что нелинейные эффекты взаимно ослабляют друг друга. Общий коэффициент ослабления ГУЧ составляет k = 7,7. Неоднородность ослабления по частоте приводит к сдвигу максимума спектра, генерируемого в нелинейной среде высокочастотного излучения на учетверённые частоты. Эти необычные нелинейные эффекты – перекрытие спектров ГУЧ и ФСМ, их неоднородное по спектру взаимное ослабление, вследствие чего происходит сдвиг частот генерируемого в изотропных средах излучения с утроенных на учетверенные, – характерны для однопериодного излучения, но полностью отсутствуют для квазимонохроматического излучения. Это означает, что для волн из малого числа колебаний мы получаем дополнительные возможности управления эффективностью и характером протекания нелинейных процессов.

Авторы выражают признательность профессору И.П. Гурову за полезные замечания и рекомендации к работе. Работа выполнена при финансовой поддержке Минобрнауки РФ в рамках Государственного задания (Паспорт No 2019-0903).