Перелеты со встречей продолжительностью не более витка между близкими околокруговыми компланарными орбитами

брагазин а.ф.

уСков а.в.

БРАГАЗИН Александр Федорович — кандидат технических наук,

Аппаратура спутниковой навигации, установленная на современных космических аппаратах (КА), значительно повысила оперативность и точность навигационного обеспечения системы управления сближением и обеспечила необходимые условия для реализации так называемых схем «быстрой» встречи КА [1, 2]. Расчетная продолжительность встречи российских кораблей серий «Союз» и «Прогресс» для исходных некомпланарных орбит с момента начала маневрирования до момента встречи в алгоритмах наведения [1, 3] ограничена снизу двумя витками. В работе [4] предложены программы встречи КА для околокруговых компланарных непересекающихся орбит, дополняющие алгоритм наведения [1, 3] для продолжительностей встречи от одного до двух витков. Программы содержат на конечном участке перелета трехимпульсную программу встречи продолжительностью виток, определенную по методу распределения импульсов оптимального межорбитального перелета. Фазирование для достижения необходимой разности фаз на начало трехимпульс-ной программы встречи обеспечивается маневрированием на предшествующем участке полета и достигается разделением импульсов оптимального межорбитального перелета, не приводящим к увеличению расхода топлива.

Программы для продолжительностей встречи не более витка рассматриваются в предлагаемой статье. Назначение продолжительности встречи в пределах витка позволяет рассмотреть возможности использования оптимального двухимпульсного перелета между околокруговыми компланарными орбитами для достижения встречи. Для продолжительности встречи, превышающей продолжительность оптимального двухим-пульсного межорбитального перелета, определены условия существования трех-импульсного перелета с фиксированным значением конечного импульса, обеспечивающего заданные априори конечные условия встречи.

Статья дополняет исследование алгоритмов встречи [4] для околокруговых компланарных непересекающихся орбит. Предложенные оптимальные решения задачи встречи продолжительностью менее двух витков содержат только трансверсальные импульсы одного направления и относятся к так называемым компланарным особым решениям в соответствии с терминологией, предложенной в работе [5].

Представление относительногодвижения ка для компланарных орбит [3]

Вектор относительного положения двух КА в проекциях на оси опорной орбитальной системы координат (ОСК), вращающейся с угловой скоростью ω0 = const, определяется как разность ∆r→ ≡ (x, y) = r→П – r→A, где r→A — вектор положения активного корабля (АК), выполняющего маневры; r→ П — вектор положения пассивного корабля, например, орбитальной станции (ОС). Аналогично определяется вектор ∆v→ относительной скорости КА. Безразмерный вектор относительного положения определяется по формуле ∆r , где R0 — радиус опорной орбиты; безразмерный вектор скорости — ∆v→ по формуле ω . В качестве независимой переменной в линеаризованных дифференциальных уравнениях движения [6] принимается центральный угол ϑ = ω0t, определяющий положение ОСК, являющийся безразмерным аналогом времени, и по отношению к ϑ в статье исполь- зуется терминология, принятая для реального времени. Параметры относительного движения АК и ОС определим по формулам:

c ₁ = x – 2 y ′ ; c ₂ = 2 y + x ′ ;

c ₃ = –3 y – 2 x ′ ; c ₄ = y ′

(штрихами помечены производные координат по аргументу ϑ ) и представим решение уравнений относительного движения в виде:

c ₁ ( ϑ ) = c ₁ ( ϑ ₀ ) – 3 c ₂ ( ϑ – ϑ ₀ );

c ₂ ( ϑ ) = c ₂ ( ϑ ₀ );

c ₃ ( ϑ ) = c ₃ ( ϑ ₀ )cos( ϑ – ϑ ₀ ) + c ₄ ( ϑ ₀ )sin( ϑ – ϑ ₀ );

c ₄ ( ϑ ) = c ₄ ( ϑ ₀ )cos( ϑ – ϑ ₀ ) – c ₃ ( ϑ ₀ )sin( ϑ – ϑ ₀ ).

Физический смысл параметров относительного движения поясняется в работах [3, 7].

реализация встречи на двухимпульсном оптимальном межорбитальном перелете между близкими околокруговыми компланарными непересекающимися орбитами

Для непересекающихся орбит АК и ОС параметры относительного движения удовлетворяют ограничению:

J = 4 c ₂ ² – c ₃ ² – c ₄ ² ≥ 0, (3) где J — инвариант невозмущенного относительного движения двух КА. Без ограничения общности далее будем полагать, что c ₂ > 0.

Оптимальный межорбитальный перелет продолжительностью менее витка содержит два трансверсальных импульса

J ∆ u ⁰ =             ;

^{1     4(2} С 2 ^{+ C}8 >

₁                                  (4)

∆u20 = 4(2c2 + c3) [(2c2 + c3)2 + c42] = с2 – ∆u10, если предположить дополнительно, что 2c2 + c3 ≠ 0.

Начало перелета ϑ ₁ — произвольный момент времени; момент окончания перелета ϑ ₂ = ϑ ₁ + τ ⁰, где

c

τ ⁰ = π + 2arctg     ⁴                   (5)

2 c + c

— продолжительность оптимального перелета, 0 ≤ τ ≤ 2 π .

При 2 c ₂ + c ₃ = 0 единственный импульс, прикладываемый в начале перелета в точке касания орбит, определяется по формуле

∆ u ₁ ⁰ = 0,25(2 c ₂ + c ₃ ² + c ₄ ² ) = c ₂ .       (6)

Графическое представление характеристик перелета содержится в работе [3].

Характеристики оптимального межорбитального перелета зависят только от параметров c ₂ , c ₃ , c ₄ , определяющих размеры и форму исходных орбит. Встреча по завершении оптимального двухимпульсного перелета достигается при условии, что на момент ϑ ₁ разность фаз встречающихся КА удовлетворяет уравнению [3]

c1(ϑ1) – Σn 3(ϑi – ϑ1)∆ui = i = 1 (7)

= c ₁ ( ϑ ₁ ) – 3 τ ⁰( ϑ ₁ ) ∆ u ₂ ⁰ ( ϑ ₁ ) = 0.

Связь (7) между параметрами относительного движения определяет положение соединения , когда одновременно с завершением межорбитального перелета достигается встреча КА.

Представим параметры относительного движения на момент ϑ1 как функции аргумента 0 ≤ ϕ ≤ 2π, отсчитываемого от момента прохождения максимального по модулю отклонения по высоте y* траектории относительного движения, и параметра формы траектории e*, определяемого как отношение минимального y** и максимального отклонения по высоте (e* = y**/y*):

c ₂ ( ϕ ) = 0,25( y * + y **) = 0,25 y *(1 + e *);

c ₃ ( ϕ ) = 0,5( y * – y **)cos ϕ =

= 0,5 y *(1 – e *)cos ϕ ;                 (8)

c ₄ ( ϕ ) = –0,5( y * – y **)sin ϕ =

= –0,5 y *(1 – e *)sin ϕ .

Без ограничения общности положим y * = 1.

Представление о совокупности положений соединения в декартовых координатах ОСК можно получить, выразив координаты как функции аргумента ϕ :

x ( ϕ ) = c ₁ *( ϕ ) + 2 c ₄ ( ϕ ) = c ₁ *( ϕ ) + 2 y ′ ( ϕ ) = c ₁ *( ϕ ) – (1 – e *)sin ϕ ;

y(ϕ) = 2c2 + c3(ϕ) = 0,5[1 + e* + (1 – e*)cosϕ], где c1*(ϕ) определяется связью (7).

Общий вид положений соединения в ОСК с началом в центре масс орбитальной станции (ОС) представлен на рис. 1. Параметром кривых является e *. Отметим, что при значениях ϕ = 0 и ϕ = π значение τ ⁰ = π, а положения соединения принадлежат выделенной синим пунк-

3 π

тиром прямой

x = y , называемой линией 4

хомановских переходов [7].

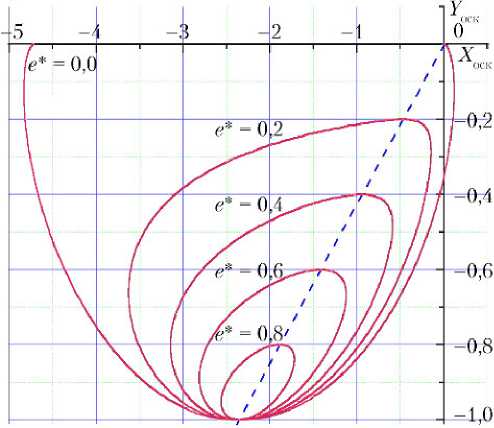
Рис. 1. Положения соединения на плоскости X0Y ОСК орбитальной станции

Возможности практического использования двухимпульсного оптимального перелета для достижения встречи ограничены, так как единственным свободным параметром является момент ϑ ₁ — начало перелета. В известных алгоритмах управления сближением [1, 3, 8] назначаются момент встречи ϑ _пр и так называемая прицельная скорость v ^→ _пр = ( V _пр , 0, 0) на момент контакта, выбираемая исходя из требований навигационного обеспечения и безопасного сближения при подлете АК к ОС. Выбором начала перелета можно обеспечить либо встречу КА в заданный момент времени, либо величину скорости в момент контакта КА в диапазоне, ограниченном апсидальными импульсами оптимального межорбитального перелета.

Будем полагать, что на момент ϑ _N разрешенного начала маневрирования заданы параметры относительного движения c ₂ , c ₃ , c ₄ .

Оптимальный двухимпульсный перелет продолжительностью τ ⁰, заканчивающийся встречей КА, начинается в момент ϑ ₁ = ϑ _пр – τ ⁰. Значение ϑ ₁ является решением трансцендентного уравнения на интервале ( ϑ _N , ϑ _пр ):

ϑ _пр – ϑ = τ ⁰( ϑ ). (10)

Рис. 2 иллюстрирует нахождение решения уравнения (10). Аргумент ϑ и функции f ( ϑ ) = ϑ _пр – ϑ ; τ ⁰( ϑ ) выражены в градусах. Решение ϑ ₁ для начала оптимального двухимпульсного перелета далее будем обозначать ϑ ₁ ⁰ по аналогии с другими характеристиками такого перелета. Оно определяется как абсцисса точки пересечения прямой f ( ϑ ) = ϑ _пр – ϑ , выделенной синим цветом, и функции τ ⁰( ϑ ) на интервале ( ϑ _N , ϑ _пр ).

как функции начала перелета ϕ , удовлетворяют очевидному ограничению

0,25 y ** ≤ ∆ u ⁰ ( ϕ ) ≤ 0,25 y *;

1                       (12)

0,25 y ** ≤ ∆ u ⁰ ₂ ( ϕ ) ≤ 0,25 y *,

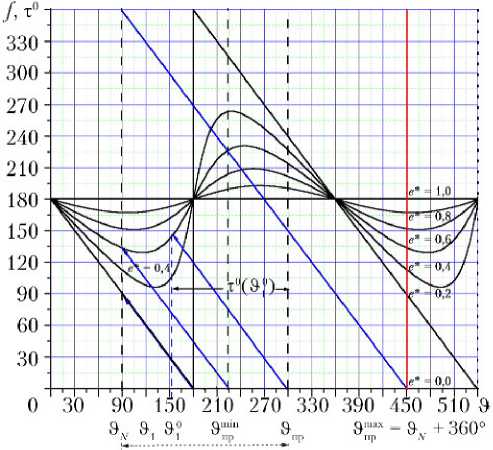
Рис. 2. Иллюстрация к решению трансцендентного уравнения (10)

где y ** и y * — отклонения вдоль радиус-вектора в апсидальных точках невозмущенного относительного движения. Если заданная величина прицельной скорости удовлетворяет неравенству

y ** ≤ 4 V _пр ≤ y *, (13)

то момент начала перехода с прицельной скоростью ∆ u ₂ ⁰ = V _пр находится из уравнения:

∆ u ₂ ⁰ = c ₂ – ∆ u ₁ ⁰ = V _пр .

С помощью формул (4), (8), получим

уравнение относительно ϕ :

2 e * – (1 + e *) 1 + e *

= (1 – e *)

1 + e *

V пр y * _

_- 4 2 nL У * .

cos ϕ .

На рисунке представлены решение ϑ ₁ ⁰ уравнения (10) для заданного ϑ _пр при фиксированном значении e * = 0,4 и интервал допустимых значений ( ϑ ^m _пр ⁱⁿ, ϑ _пр ), а также максимальный в предположениях задачи интервал ( ϑ _N , ϑ ^m _пр ^ax) продолжительностью виток. Будем предполагать, что заданное значение ϑ _пр ≥ ϑ ^m _пр ⁱⁿ. Очевидно, граница ϑ ^m _пр ⁱⁿ определяется по формуле

ϑmin = ϑ + τ0(ϑ ), (11) пр N N , где τ0(ϑN) — продолжительность оптимального перелета, начинающегося в момент ϑN, рассчитывается по формуле (5). Разность фаз на момент начала перелета определяется связью (7). Разность фаз на момент ϑN определяется по формуле прогнозирования переменной c1(ϑ).

Параметры, определяющие размер и форму исходных орбит КА, ограничивают возможность назначения произвольного значения V _пр при реализации оптимального двухимпульсного межорбитального перелета. В самом деле, значения импульсов, рассматриваемые

Напомним, что ϕ отсчитывается от большей по величине апсиды траектории относительного движения. В соответствии с формулами (8) аргумент ϕ _N этой апсиды на момент ϑ _N определяется через параметры c ₃ ( ϑ _N ) и c ₄ ( ϑ _N ). Начало перелета ϑ ₁ нетрудно привязать к ϑ _N :

ϑ ₁ = ϑ _N + ( ϕ – ϕ _N ).

Очевидно, момент встречи не может задаваться независимо от V _пр и определяется по формуле ϑ _пр = ϑ ₁ + τ ⁰( ϑ ₁ ), где τ ⁰( ϑ ₁ ) — продолжительность перелета. Разность фаз на момент начала перелета определяется связью (7). Значение c ₁ ( ϑ _N ) на разрешенное начало маневрирования определяется по формулам прогнозирования невозмущенного движения.

оптимальная трехимпульсная встреча для непересекающихся орбит

Для обеспечения заданной прицельной скорости V _пр в заданный момент встречи ϑ _пр рассмотрим трехимпульсную программу с трансверсальными импульсами. Для фиксированного начала перелета ϑ ₁ всегда существует оптимальный двухимпульсный межорбитальный перелет продолжительностью τ ⁰( ϑ ₁ ), рассчитываемый по формулам (4)–(6). Будем

далее полагать, что заданный момент встречи ϑ _пр >  ϑ ₁ + τ ⁰( ϑ ₁ ), а программа встречи имеет вид

ϑ 1	ϑ 2	ϑ 3 = ϑ пр
∆ u 1	∆ u 2	∆ u 3 = V пр .

Представим уравнения связи между параметрами движения и импульсами [3] в следующем виде:

c ₁ ( ϑ ₁ ) – 3( ϑ ₂ – ϑ ₁ ) ∆ u ₂ – 3( ϑ _пр – ϑ ₁ ) V _пр = 0;

c ₂ ( ϑ ₁ ) – ∆ u ₁ – ∆ u ₂ – V _пр = 0;

c ₃ ( ϑ ₁ ) + 2 ∆ u ₁ + 2 ∆ u ₂ cos( ϑ ₂ – ϑ ₁ ) +

+ 2 V _пр cos( ϑ _пр – ϑ ₁ ) = 0;                  (15)

c ₄ ( ϑ ₁ ) + 2 ∆ u ₂ sin( ϑ ₂ – ϑ ₁ ) +

+ 2 V пр sin( ϑ пр – ϑ 1 ) = 0.

Последние три уравнения системы (15) определяют характеристики ∆ u ₁ , ∆ u ₂ , ϑ ₂ межорбитального перелета, начинающегося в момент ϑ = ϑ ₁ . Выделим их как отдельную систему:

c ₂ ′ – ∆ u ₁ – ∆ u ₂ = 0;

c ₃ ′ + 2 ∆ u ₁ + 2 ∆ u ₂ cos τ = 0;              (16)

c4′ + 2∆u1sinτ = 0, где c2′ = c2′ (ϑ1) = c2(ϑ1) – Vпр;

c 3 ′ = c 3 ′ ( ϑ 1 ) = c 3 ( ϑ 1 ) + 2 V пр cos( ϑ пр – ϑ 1 ); (17)

c 4 ′ = c 4 ′ ( ϑ 1 ) = c 4 ( ϑ 1 ) + 2 V пр sin( ϑ пр – ϑ 1 );

τ = ϑ ₂ – ϑ ₁ .

Система (16)–(17) определяет оптимальный двухимпульсный перелет с началом в произвольный момент ϑ = ϑ ₁ только для непересекающихся компланарных орбит. Представим инвариант относительного движения с параметрами c _i ′ ( i = 2, 3, 4) в виде:

J = 4 c ₂ ′ ² – c ₃ ′ ² – c ₄ ′ ² = 4 c ₂ ² – c ₃ ² –

– c 4 ² – 4 V пр y ⁰( ϑ пр ) = J 0 – 4 V пр y ⁰( ϑ пр ), где

J ₀ = 4 c ₂ ² – c ₃ ² – c ₄ ² =

= (2c2 + c32 + c42)(2c2 – c32 + c42) = y*y**, y0(ϑпр) = 2c2 + c3cos(ϑпр – ϑ1) +

+ c ₄ sin( ϑ _пр – ϑ ₁ ).

Условие непересечения орбит принимает вид:

J 0 – 4 V пр y ⁰( ϑ пр ) ≥ 0.                (18)

Отсюда, в частности, следует, что оптимальное решение существует даже для исходных орбит, касающихся в момент ϑ = ϑ _пр , если c ₂ – V _пр ≥ 0.

Решением системы (16)–(17) является оптимальный двухимпульсный перелет с начальной орбиты, определяемой параметрами c _i ( ϑ ₁ ) ( i = 2, 3, 4) движения относительно круговой опорной орбиты, на некоторую промежуточную орбиту, при движении по которой в момент ϑ ₃ = ϑ _пр достигается цель. На момент ϑ = ϑ ₂ параметры относительного движения, определяющие промежуточную орбиту, суть:

c 2 ( ϑ 2 ) = V пр ;

c 3 ( ϑ 2 ) = –2 V пр cos( ϑ пр – ϑ 2 );       (19)

c4(ϑ2) = –2Vпрsin(ϑпр – ϑ2), и значения ординат апсидальных точек траектории относительного движения в орбитальной системе координат:

y = 2 c +    c ² + c ² = 4 V ;

α 2         3     4        пр yπ = 2c2 – c32 + c42 = 0, т. е. переходная орбита касается орбиты ОС. Траектория перелета с момента ϑ2 до момента ϑ3 = ϑпр является частью траектории хомановского перелета между близкими околокруговыми компланарными орбитами. В самом деле, представим декартовы координаты в ОСК корабля на момент ϑ2 через параметры относительного движения:

x ( ϑ ₂ ) = c ₁ ( ϑ ₂ ) + 2 c ₄ ( ϑ ₂ ) =

= V пр [3( ϑ пр – ϑ 2 ) – 4sin( ϑ пр – ϑ 2 )];        (20)

y ( ϑ 2 ) = 2 c 2 ( ϑ 2 ) + с 3 ( ϑ 2 ) = 2 V пр [1 – cos( ϑ пр – ϑ 2 )].

Формулы (20) являются параметрическим представлением траектории хомановского перелета на отрезке [ ϑ ₂ , ϑ _пр ]. Для представления траектории в ОСК ОС в формулах (20) следует изменить знаки x ( ϑ ₂ ) и y ( ϑ ₂ ) на противоположные.

В уравнениях (15)–(17) варьируемые моменты начала и конца перелета удовлетворяют ограничениям ϑ _N ≤ ϑ ₁ <  ϑ _пр и ϑ _пр – ϑ _N ≤ 2 π . Обозначим ∆ϑ = ϑ _пр – ϑ ₁ , где ∆ϑ ≥ τ ⁰( ϑ ₁ ).

Если ∆ϑ = τ ⁰( ϑ ₁ ), то трехимпульсный перелет в точку встречи вырождается в двухимпульсный перелет.

Если ∆ϑ = 2 π , то трехимпульсный перелет для встречи, начинающийся в момент ϑ ₁ = ϑ _N и рассчитанный по уравнениям (16)–(17), иллюстрирует метод распределения (расщепления) импульсов двухимпульсного межорбитального перелета [7] между исходными орбитами АК и ОС. В этом случае первый импульс ∆ u ₁ ⁰ межорбитального перелета делится на два импульса программы встречи следующим образом:

∆ u ₁ ( ϑ ₁ ) = ∆ u ₁ ⁰ – V _пр ;

∆ u 3 ( ϑ пр ) = ∆ u 3 ( ϑ 1 + 2π) = V пр .

Если τ ⁰( ϑ ₁ ) <  ∆ϑ ≤ 2 π , то уравнения (15)–(17) позволяют определить множество трехимпульсных перелетов с заданной прицельной скоростью V _пр . Далее рассматриваются два типа перелетов, представляющих практический интерес.

• 1.    Трехимпульсные перелеты первого типа. Начало перелета ϑ ₁ — варьируемый параметр, конец перелета ϑ _пр — фиксированный параметр. Фиксация конца перелета используется, например, для обеспечения приемлемых условий освещенности на случай перехода к ручному управлению, для обеспечения резервирования связи между кораблем и ЦУП на конечном участке встречи.

• 2.    Трехимпульсные перелеты второго типа. Начало перелета ϑ ₁ — фиксированный параметр, конец перелета ϑ _пр — варьируемый параметр. Перелет используется для обеспечения минимальной продолжительности операции с момента выведения.

Будем полагать, что для заданных на момент ϑ = ϑ _N параметров относительного движения неравенство (18) справедливо.

Рассмотрим трехимпульсные перелеты первого типа. Найдем решение уравнения (10), определяющего момент ϑ ₁ ⁰ начала оптимального двухимпульсного перелета, заканчивающегося встречей в момент ϑ _пр . Начало ϑ ₁ трехимпульсного перелета назначим на интервале ( ϑ _N , ϑ ₁ ⁰). Тогда назначенная продолжительность трех-импульсного перелета ϑ _пр – ϑ ₁ >  τ ⁰( ϑ ₁ ⁰).

Первые два импульса трехимпульс-ного перелета составляют оптимальный перелет с исходной орбиты корабля на промежуточную хомановскую орбиту, при движении по которой в момент ϑ = ϑ _пр обеспечивается заданная прицельная скорость V _пр . Продолжительность τ двухимпульсного перелета на промежуточную орбиту рассчитывается по формуле (5) для параметров относительного движения c ′ _i ( ϑ ₁ ) ( i = 2, 3, 4).

Для существования трехимпульсного перелета необходимо, чтобы было удовлетворено неравенство:

ϑ ₁ + τ ( ϑ ₁ ) <  ϑ _пр .                    (21)

Покажем, что, если ϑ ₁ <  ϑ ₁ ⁰, то (21) справедливо. Рассмотрим функцию

f(ϑ) = ϑ + τ0(ϑ) = ϑ + π + 2arctg c 4(S)

2 c ₂ + c₃(9)

где τ ⁰( ϑ ) — продолжительность оптимального двухимпульсного перелета для исходных орбит. Производная этой функции с помощью (8) представляется в виде:

f ′ ( ϑ )

2 e*

(1 - e *²)cos 9 + (1 + e *²)

и положительна при e * > 0. Поскольку ϑ ₁ ⁰ — решение уравнения (10), то

ϑ10 + τ(ϑ10) = ϑпр, и для ϑ1<ϑ10 справедливо неравенство

ϑ ₁ + τ ⁰( ϑ ₁ ) <  ϑ _пр .                     (22)

Для справедливости неравенства (21) достаточно показать, что

τ ( ϑ ₁ ) ≤ τ ⁰( ϑ ₁ ).                        (23)

Поскольку arctgx — монотонно возрастающая функция при –∞ ≤ x ≤ ∞, преобразуем неравенство (23) с помощью формулы (5) к виду c′4 ≤ c4 2c′2 + c′3 2c2 + c3 , и подставим переменные ci (i = 2, 3, 4), определенные по формулам (17). Используя уравнения (9) и (17), перепишем неравенство (23) в виде у ‘(9,) + 2 KpSWnp — 91)      у '(9J

≤ ^, y ( ϑ ₁ ) + 2 V _пр [cos( ϑ _пр – ϑ ₁ ) – 1]      y ( ϑ ₁ )

после несложных преобразований приведем к неравенству y′(ϑ1)       sin(ϑпр – ϑ1)   ,

y ( ϑ ₁ ) ^≤ cos( ϑ _пр – ϑ ₁ ) – 1

которое равносильно неравенству ctg

^{τ 0 ( ϑ 1 )}

ϑ – ϑ пр 1

≥ ctg ₂

.

Последнее неравенство равносильно неравенству (22), и существование трехимпульсных перелетов для 9 1 <  9 0 доказано.

Разность фаз на фиксированное начало 9 = 9 1 трехимпульсного маневра встречи, определяющая единственное положение соединения для заданных параметров относительного движения с ( 9 1 ) ( i = 2, 3, 4) и параметров встречи 9 _пр , V , рассчитывается с помощью первого уравнения системы (15) по формуле:

с 1 *( 9 1 ) = 3 тА u ₂ + 3 А9 V пр . (24)

Параметры относительного движения на начало маневрирования 9 = 9 N определяются по формулам прогнозирования невозмущенного движения (2). Положение соединения достигается при пассивном полете с момента 9 = 9

N до момента 9 = 9 ₁ .

На рис. 3 представлены границы оптимального диапазона разности фаз с ₁ ^min( 9 ) = с 1 *( 9 ) и с m ^ax( 9 ) для трех-импульсных перелетов с варьируемым моментом 9 ( 9 N < 9 <  9 0 ) приложения первого импульса. Расчет произведен для параметра e * = 0,6.

На момент 9 N = 0 значение параметра, определяющего ориентацию разности векторов эксцентриситетов, ф = 90 ° . Фиксированный параметр 9 п _р = 360 ° . Значения 9 N и 9 _пр представлены на рисунке вертикальными прямыми.

Продолжительность оптимального двухимпульсного перелета между исходными орбитами т ⁰ = 208,07 ° , отсюда следует, что 9 0* = 151,93 ° . Нижняя граница диапазона определена по формуле (24).

Верхняя граница диапазона разности фаз определена по формуле:

с 1 ^тах( 9 ) = с ₁ *( 9 ⁰) + 3 с ₂ ( 9 ⁰ - 9 ).     (25)

Пунктирные линии на рисунке соответствуют пассивному полету корабля с момента 9N до момента 91 начала трехимпульсного перелета со встречей

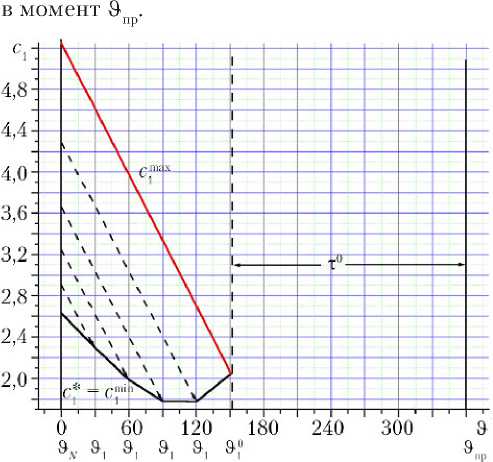
Рис. 3. Диапазон оптимальных фаз для трехимпульсных перелетов первого типа

На рис. 4 представлены траектории относительного движения с момента 9 _N до момента 9 _пр . На момент 9 N все траектории начинаются на линии с разностью высот y = 0,8, траектории отличаются значением момента первой коррекции 9 1 , координаты первой коррекции трехимпульсного перелета отмечены на рисунке красным кружком.

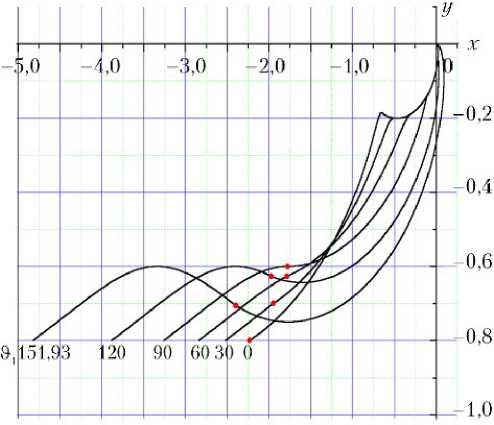
Рис. 4. Траектории относительного движения с мо мента 9N до момента 9пр для перелетов первого типа

Рассмотрим перелеты второго типа. Будем считать, что оптимальный двух-импульсный перелет начинается в момент 3 = 3 N а его продолжительность — т ° ( 3 N ). Трехимпульсные перелеты с закрепленным началом 3 1 = 3 N существуют, если назначаемый момент окончания перелета 3 _п варьируется на интервале 3 N + т ° ( 3 N ) < ^Р3 _пр <  3 N + 2 п . В самом деле, продолжительность двухимпульсного перелета, определяемого системой уравнений (16)–(17), не превышает продолжительности оптимального двухимпульс-ного перелета между исходными орбитами АК и ОС, если оба перелета начинаются в один и тот же момент времени. Очевидно, что минимальное значение 3 _пр для трехимпульсного перелета второго типа

3min = 3„ + т°(3,) + е, пр N         N , где е > ° — сколь угодно малая величина.

Разность фаз на фиксированное начало 3 1 = 3 N трехимпульсного маневра встречи, определяющая единственное положение соединения, рассчитывается по формуле (24) и представлена на рис. 5. Исходные параметры относительного движения на момент 3 1 = 3 N = ° суть e * = 0,6; ф (°) = 90 ° . Назначаемый момент встречи 3 _п варьируется на интервале т ° (°) <  3 _пр < 36 п ° ° , где т ° (°) = 151,93 ° .

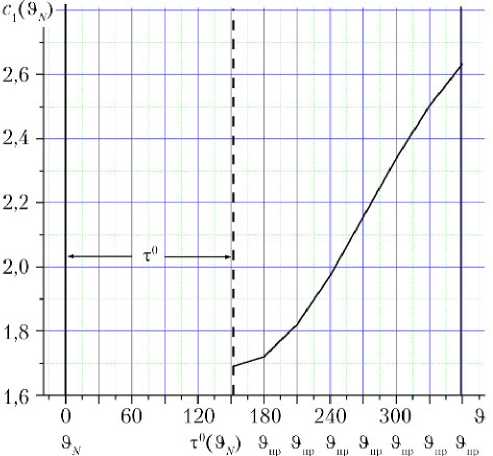
Рис. 5. Оптимальная разность фаз на начало трехим-пульсных перелетов второго типа

На рис. 6 представлены траектории относительного движения с момента 3N= ° до назначенного (варьируемого) момента 3пр. На момент 3N все траектории начинаются на линии с разностью высот y = 0,8. Красным цветом выделена траектория двухимпульсного перелета со встречей.

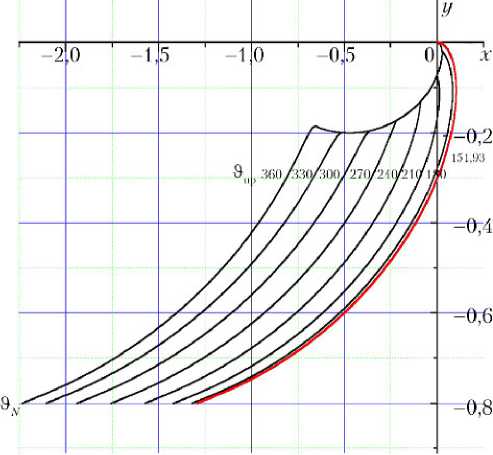
Рис. 6. Траектории относительного движения с момента 3 N = 0 до варьируемого момента 3 _пр для перелетов второго типа

Построение трехимпульсных перелетов для заданных параметров относительного движения

Перелеты первого типа ( с фиксацией 3 _пр ). Первый этап построения перелета — решение трансцендентного уравнения (10) относительно 3 ₁ ^°, определяющего верхнюю границу значений 3 1 для начала трехимпульсных перелетов, 3 N <  3 1 <  3 ° . Верхняя граница диапазона оптимальных фаз на момент 3 N определяется по формулам (24) и (25). Нижняя граница — c mi ⁿ( 3 N ) = c *( 3 N ).

Трехимпульсный перелет для заданных значений ci(3N) (i = 1, 2, 3, 4) существует при условии, что c min(3 n) < c 1(3 n ) < c max(3 n ).         (26)

Момент 31 начала перелета находится как решение трансцендентного уравнения на интервале 3N < 31 < 3° c 1(3) = c min(3),                      (27)

где нижняя граница оптимальных фаз c1min(3) определяется по формуле (24) и достигается после пассивного полета с момента 3N до момента 3. Разность фаз на момент 3 определяется по формуле c 1(3) = c 1(3n) - 3c2(3 - 3n).        (28)

На рис. 3 моменты 3 1 определяются как точки пересечения пунктирных прямых (28) с функцией c 1 *( 3 ) = c “ⁿ ( 3 ).

При подготовке полета АК достаточно хорошо известны характеристики ракетоносителя, определяющие размер и форму орбиты АК, т. е. параметры c ₂ , c ₃ , c ₄ относительного движения АК и ОС на момент 3 N разрешенного начала маневрирования. Разность фаз назначается, исходя из неравенства (26).

Перелеты второго типа (с фиксацией 31 = 3N). Продолжительность т0(3N) оптимального двухимпульсного перелета определяется по формуле (5). Разность фаз на фиксированное начало 31 = 3N трехимпульсного маневра встречи рассчитывается по формуле (24). Нижняя граница диапазона разностей фаз соответствует 3п = т0(3 N); верхняя граница 3 = ^max, р е ^max ^ 3 , 2^  — априори пр пр               пр N заданная продолжительность трехим-пульсного перелета. Значение параметра c 1(3 N) должно удовлетворять неравенству вида (26). Значение 3пр находится как решение уравнения c 1(3N) = c*(3N, 3пр),                 (29)

где c *( ³ n ³ пр ) = 3 тА и 2 ⁺ Жр - ³ N ) V _,, в соответствии с формулой (24).