Перелеты со встречей продолжительностью от одного до двух витков между околокруговыми компланарными орбитами

брагазин а.ф.

уСков а.в.

Алгоритм управления сближением российских кораблей серий «Союз» и «Прогресс» для исходных некомпланарных орбит [1, 2] имеет структурное ограничение на расчетную продолжительность встречи с момента начала маневрирования до момента встречи. План встречи предусматривает реализацию двух межорбитальных перелетов, разделенных участком полета по промежуточной орбите фазирования. Для продолжительности первого оптимального перелета между некомпланарными орбитой выведения и орбитой фазирования необходимо зарезервировать виток [3]. На последнем витке встречи для обеспечения преемственности алгоритма управления сохранен многократно отработанный трехимпульсный перелет продолжительностью виток с фиксацией относительной скорости в момент встречи. Отсюда, в частности, следует, что расчетная продолжительность встречи для алгоритма, описанного в работах [1, 2], ограничена снизу двумя витками. В статье [1] отмечено, что ограничение обусловлено требованием оптимальности первого перелета, и при снятии этого требования можно определить перелет на фазирующую орбиту продолжительностью менее витка, удовлетворяющий заданной априори характеристической скорости (располагаемому запасу топлива) на операцию.

Наше внимание привлекла возможность создания программ встречи для практически важного класса компланарных непересекающихся орбит космических аппаратов (КА) с использованием метода распределения импульсов оптимального межорбитального перелета [4]. Ограничим расчетную продолжительность операции встречи с начала маневрирования до момента контакта КА продолжительностью двух периодов обращения по опорной орбите (двух витков). Тогда оптимальные программы встречи по методу распределения импульсов могут быть определены для ограниченного набора продолжительностей встречи

T* = 2π; 2π + τ0(ϑ); 4π, где τ0(ϑ) — продолжительность оптимального межорбитального перелета на произвольный момент ϑ его начала. При заданном моменте встречи ϑпр начало программы встречи — момент приложения первого импульса — определяется как ϑ1 = ϑпр – T*. Характеристики перелета — его продолжительность и величины трансверсальных импульсов — являются функциями размеров и формы исходных орбит КА и определяют ограниченный диапазон разностей фаз на момент приложения первого импульса программы межорбитального перелета, заканчивающегося встречей КА. Значения разности фаз из упомянутого диапазона называются далее положениями соединения для встречи КА.

Для встречи продолжительностью от одного до двух витков предлагается дополнить каждую из программ, полученных по методу распределения импульсов, трансверсальным импульсом фазирования, обеспечивающим достижение положения соединения на момент начала программы. В дополняемых программах встречи моменты приложения и величины распределяемых импульсов межорбитального перелета предлагается определять с учетом реализации дополнительного импульса. Будем далее полагать, что знак дополнительного трансверсального импульса совпадает со знаком разности больших полуосей орбит КА, и в результате приложения дополнительного импульса орбиты КА остаются в классе непересекающих-ся орбит. Тогда на момент приложения дополнительного импульса можно определить диапазон фаз, для которых совпадают минимумы характеристической скорости встречи и межорбитального перелета.

реализация встречи на двухимпульсном межорбитальном перелете

Для непересекающихся орбит активного корабля (АК) и орбитальной станции (ОС) параметры относительного движения, определенные в Приложении (П1)–(П5), удовлетворяют ограничению

J ≡ 4 c ₂ ² – c ₃ ² – c ₄ ² ≥ 0, (1)

где J — инвариант невозмущенного относительного движения двух КА. Без ограничения общности далее будем полагать, что c ₂ > 0.

Минимуму характеристической скорости соответствует двухимпульсный перелет с трансверсальными импульсами

J

^A u ¹    4(2 с ₂ + c₃) ’

^A u ² = 4(2 c ₂ + c₃) ^[(2 c ^{2 +} c 3 ) ⁺ c ^4],

если предположить дополнительно, что 2 c ₂ + c ₃ ≠ 0.

Импульсы прикладываются в моменты ϑ ₁ и ϑ ₂ = ϑ ₁ + τ⁰, где

c

τ0 = π + 2arctg      4                (3)

2 c ₂ + c₃)

— продолжительность оптимального перелета, 0 ≤ τ ≤ 2π.

При 2 c ₂ + c ₃ = 0 единственный импульс, прикладываемый в начале перелета в точке касания орбит, определяется по формуле:

Δ u ₁ ⁰ = 0,25(2 c ₂ + c ₃ ² + c ₄ ² ) = c ₂ .    (4)

Графическое представление характеристик перелета содержится в работе [2].

Встреча по завершении оптимального двухимпульсного перелета достигается при условии, что на момент ϑ ₁ приложения первого импульса разность фаз встречающихся КА удовлетворяет первому уравнению системы (П6) Приложения:

c ₁ (ϑ ₁ ) – 3τ⁰Δ u ₂ ⁰ = 0.             (5)

Связь (5) между параметрами относительного движения определяет положение соединения , когда одновременно с завершением межорбитального перелета достигается встреча КА. Пусть на момент разрешенного начала маневрирования ϑ _N известны значения параметров относительного движения c _i (ϑ _N ), i = 1, 2, 3, 4. Задача определения положений соединения и существования двухимпульсных перелетов в точку встречи сводится к определению области существования и нахождению решений ϑ ₁ ≥ ϑ _N трансцендентного уравнения (5). Решение задачи существует и единственно [2].

Программы встречи, сформированные с помощью метода распределения импульсов межорбитального перелета

Основные положения по управлению сближением КА на последнем витке операции встречи изложены в работах [1, 2]. План встречи в плоскости опорной орбиты содержит трехимпульсную программу перелета с промежуточной орбиты фазирования в заданную априори прицельную точку с фиксированной прицельной скоростью Vпр. Для заданной продолжительности перелета T* = 2π единственный оптимальный перелет может быть получен делением первого импульса Δu10 оптимального межорбитального двухимпульсного перелета на две части. Для непересекаю-щихся исходных орбит характеристическая скорость межорбитального перелета не зависит от момента его начала, и оптимальный перелет для встречи КА при априори заданном моменте встречи ϑпр начинается за виток до его окончания.

Программа трехимпульсного перелета со встречей имеет вид:

ϑ = ϑ ₁                   ϑ ₂ = ϑ ₁ + τ⁰(ϑ ₁ )

ϑ ₃ = ϑ _пр = 2π + ϑ ₁

Δ u ₁ = Δ u ₁ ⁰(ϑ ₁ ) – V _пр

Δ u ₂ = Δ u ₂ ⁰(ϑ ₁ )

Δ u ₃ = V _пр ,

где ϑ ₁ = ϑ _пр – 2π — момент начала трех-импульсного перелета, когда реализуется первый трансверсальный импульс Δ u ₁ = Δ u ₁ ⁰ – V _пр ; ϑ ₂ = ϑ ₁ + τ⁰ — момент приложения второго импульса Δ u ₂ = Δ u ₂ ⁰ программы; ϑ ₃ = ϑ _пр — момент приложения фиксированного импульса Δ u ₃ = V _пр .

Характеристики Δ u ₁ ⁰, Δ u ₂ ⁰, τ⁰ оптимального перелета, формирующего программу встречи на момент ϑ ₁ , зависят только от параметров исходных орбит КА, определяющих их размеры и форму, а в относительном движении — от c ₂ (ϑ ₁ ), c ₃ (ϑ ₁ ), c ₄ (ϑ ₁ ), которые рассчитываются по формулам прогнозирования относительного движения:

c ₂ (ϑ ₁ ) = c ₂ (ϑ _N );

c ₃ (ϑ ₁ ) = c ₃ (ϑ _N )cosΔϑ + c ₄ (ϑ _N )sinΔϑ;

c4(ϑ1) = c4(ϑN)cosΔϑ – c3(ϑN)sinΔϑ, где Δϑ = ϑ1 – ϑN.

Программа встречи определяет параметр c ₁ *(ϑ ₁ ) — разность фаз на момент начала трехимпульсного перелета со встречей — в функции характеристик перелета в предположении пассивного полета АК до момента ϑ ₁ . Будем иметь:

c ₁ *(ϑ ₁ ) = 6π V _пр + 3τ⁰(ϑ ₁ )Δ u ₂ ⁰(ϑ ₁ ).     (8)

Для коэллиптических орбит c1*(ϑ1) = 6πVпр + 1,5πc2(ϑN) = const.

Отметим, что формулы (7) и (8) позволяют рассматривать c ₁ *(ϑ ₁ ) как разность фаз на произвольное начало трехимпульс-ной программы встречи ϑ ₁ = ϑ _N + Δϑ _N . Момент встречи тогда определяется как ϑ _пр = ϑ ₁ + 2π. Величина разности фаз на момент ϑ ₁ в пассивном полете АК в соответствии с уравнениями движения определяется по формуле:

c ₁ (ϑ ₁ ) = c ₁ (ϑ _N ) – 3 c ₂ (ϑ _N ) (ϑ ₁ – ϑ _N ),    (9)

т. е. является функцией Δϑ _N = ϑ ₁ – ϑ _N .

Представим выражение для положения соединения (8) в виде:

c ₁ *(ϑ _N + Δϑ _N ) =

= 6π V _пр +3τ⁰(ϑ _N + Δϑ _N )Δ u ₂ ⁰(ϑ _N + Δϑ _N ).

Значение промежутка ΔϑN пассивного полета до достижения положения соединения определяется из уравнения c1(ϑN + ΔϑN) = c1*(ϑN + ΔϑN). (11)

Если c ₁ (ϑ _N ) ≥ c ₁ *(ϑ _N ), то решение уравнения (11) существует и является единственным. Если оно удовлетворяет ограничениям 0 ≤ Δϑ _N < 2π и ϑ _N + Δϑ _N + 2π < ϑ _пр , где ϑ _пр — априори назначенный момент встречи, то можно рассмотреть возможность достижения встречи ранее момента ϑ _пр .

В общем случае положение соединения в фиксированный момент ϑ ₁ = ϑ _пр – 2π может быть достигнуто после приложения в момент ϑ _N ≤ ϑ < ϑ ₁ импульса Δ u (ϑ) ≠ 0, регулирующего скорость изменения разности фаз.

В случае, если c ₁ (ϑ ₁ ) >  c ₁ *(ϑ ₁ ), движение к положению соединения можно охарактеризовать как медленное. Регулирование скорости изменения фазы производится с помощью трансверсального импульса, изменяющего среднюю разность высот. В данном случае в момент ϑ следует приложить импульс Δ u < 0, увеличивающий параметр c ₂ в относительном движении. Очевидно, что с увеличением c ₂ характеристическая скорость встречи оказывается больше характеристической скорости оптимального межорбитального перелета между исходными орбитами. Отсюда, в частности, следует, что для оптимальной встречи максимальное значение разности фаз на момент ϑ соответствует пассивному перелету с момента ϑ до момента начала трехимпульсного перелета в точку встречи ϑ ₁ = ϑ _пр – 2π и определяется по формуле:

c ₁ ^max(ϑ) = 3 c ₂ (ϑ ₁ – ϑ) + + 6π V _пр + 3τ⁰(ϑ ₁ )Δ u ₂ ⁰(ϑ ₁ ).

В правой части выражения (12) — функция переменных c _i (ϑ ₁ ), i = 2, 3, 4, которые рассчитываются по формулам (7) прогнозирования невозмущенного движения.

ϑ               ϑ ₁ = ϑ + Δϑ

Δu(ϑ)            Δu1 = Δu10(ϑ1) – Vпр где Δϑ = ϑ1 – ϑ = ϑпр – 2π – ϑ.

Далее полагается, что исходная орбита АК и орбита, получаемая после приложения импульса Δ u (ϑ), не пересекаются с орбитой ОС. Обозначим параметры относительного движения в момент ϑ до приложения импульса Δ u (ϑ) как c ₂ , c ₃ , c ₄ , а после приложения импульса — как B , D , E :

B = c ₂ – Δ u ;

D = c ₃ + 2Δ u ;             (14)

E = c ₄ .

Представим связь инвариантов (1) относительного движения до и после приложения импульса Δ u (ϑ) в виде:

4 c ₂ ² – c ₃ ² – c ₄ ² = 4 B ² – D ² – E ² + 4Δ u (ϑ) y (ϑ). (15)

Из формул (2), определяющих величину первого импульса межорбитального перелета, находим следующее представление инвариантов:

4 c ₂ ² – c ₃ ² – c ₄ ² = 4Δ u ₁ ⁰ (ϑ) y (ϑ);

4 B ² – D ² – E ² = 4Δ u ₁ ⁰ (ϑ ₁ ) y (ϑ ₁ ).

В формулах (16) Δ u ₁ ⁰ (ϑ) — импульс в момент ϑ для оптимального перелета с орбиты выведения на орбиту ОС, если y (ϑ) ≠ 0, Δ u ₁ ⁰(ϑ ₁ ) — импульс в момент ϑ ₁ = ϑ _пр – 2π для оптимального перелета с фазирующей орбиты на орбиту ОС, если y (ϑ ₁ ) ≠ 0. Орбиты АК и ОС после приложения импульса Δ u (ϑ) не пересекаются, если Δ u (ϑ) ≤ Δ u ₁ ⁰ (ϑ).

С учетом формул (16) связь (15) примет вид:

Δ u ₁ ⁰(ϑ ₁ ) y (ϑ ₁ ) = Δ u ₁ ⁰(ϑ) y (ϑ) – Δ u (ϑ) y (ϑ). (17)

Если после приложения импульса Δ u (ϑ) фазирующая орбита в момент ϑ ₁ касается орбиты ОС, т. е. y (ϑ ₁ ) = 0, то Δ u (ϑ) = Δ u ₁ ⁰(ϑ), а ϑ ₁ – ϑ = τ⁰(ϑ). Для y (ϑ ₁ ) ≠ 0 из уравнения (17) находим:

Y (9)

Δ u ⁰(ϑ ) = [Δ u ⁰(ϑ) – Δ u (ϑ)]       .     (18)

1 ^{1          1}                      Y ^{( 9} i)

В случае, если c ₁ (ϑ ₁ ) <  c ₁ *(ϑ ₁ ), относительное движение активного корабля и орбитальной станции следует замедлить, реализовав в момент ϑ _N < ϑ < ϑ ₁ дополнительный импульс Δ u > 0, уменьшающий среднюю разность высот. Программа встречи принимает вид:

ϑ ₂ = ϑ ₁ + τ⁰(ϑ ₁ ) Δ u ₂ = Δ u ₂ ⁰(ϑ ₁ )

ϑ = ϑ + 2π

Δ u ³ = V ¹,      ⁽¹³⁾

3 пр

Перелет с момента ϑ ₁ до момента ϑ _пр является оптимальным, если

Δ u ₁ ⁰ (ϑ ₁ ) ≥ V _пр ;    Δ u ₂ ⁰(ϑ ₁ ) ≥ 0.         (19)

Тогда все импульсы трехимпульсной программы на отрезке [ϑ ₁ , ϑ _пр ] имеют один знак, совпадающий со знаком c ₂ (ϑ ₁ ). С учетом формулы (18) первое неравенство (19) равносильно неравенству

Y (9,)

A u (9) < A u 0(9) - V пр^(^.     (20)

В неравенстве (20) представим

y (ϑ) = 2 c ₂ (ϑ) + c ₃ (ϑ);

y (ϑ ₁ ) = 2( c ₂ (ϑ) – Δ u ) + ( c ₃ (ϑ) + 2Δ u )×   ⁽²¹⁾

× cosΔϑ + c ₄ (ϑ)sinΔϑ = y ⁰(ϑ ₁ ) – 2Δ u (1 – cosΔϑ);

y ⁰(ϑ ₁ ) = 2 c ₂ (ϑ) + c ₃ (ϑ)cosΔϑ + c ₄ (ϑ)sinΔϑ.

Подставляя представления y (ϑ) и y (ϑ ₁ ) из (21) в неравенство (20), получим для предельного случая, когда Δ u ₁ ⁰(ϑ ₁ ) = V _пр , формулу для максимального значения импульса Δ u (ϑ), справедливую для y (ϑ ₁ ) ≠ 0:

∆ u ⁰(ϑ) y (ϑ) – V y⁰ (ϑ )

^{Δ u max( ϑ ) =} y (ϑ¹) – 2 V пр(1 –^пc^рos∆ϑ¹)^{. (22)}

Для определения нижней границы диапазона оптимальных фаз в функции текущего времени можно воспользоваться трактовкой формулы (22) как импульса, обеспечивающего максимальное торможение относительного движения в момент ϑ, где ϑ _N ≤ ϑ ≤ ϑ ₁ . Минимальная разность фаз на момент ϑ определяется по формуле:

c ₁ ^min(ϑ) = 3Δϑ[ c ₂ (ϑ) – Δ u ^max(ϑ)] + + 6π V _пр + 3τ⁰(ϑ ₁ )Δ u ₂ ⁰(ϑ ₁ ),

где характеристики оптимального межорбитального перелета на момент ϑ ₁ рассчитываются с учетом влияния импульса Δ u ^max(ϑ).

В случае Δϑ = ϑ ₁ – ϑ = 0 очевидно, что y ⁰(ϑ ₁ ) = y (ϑ), а импульс Δ u ^max(ϑ) совпадает с первым импульсом трехимпульсного перелета продолжительностью один виток:

Δ u ^max(ϑ) = Δ u ₁ (ϑ ₁ ) = Δ u ₁ ⁰ (ϑ ₁ ) – V _пр . (24)

Программа встречи (13) ожидаемо превращается в трехимпульсную программу (6). Параметры движения на момент ϑ = ϑ ₁ рассчитываются по формулам невозмущенного движения, а минимальная разность фаз на момент ϑ ₁ , рассчитываемая по формуле (23), совпадает со значением, определяемым по формуле (8). Для продолжительности встречи один виток верхняя и нижняя границы диапазона оптимальных фаз на момент приложения первого импульса совпадают.

В случае Δϑ = ϑ ₁ – ϑ = τ⁰(ϑ) импульс Δ u ^max(ϑ) = Δ u ₁ ⁰(ϑ), а фазирующая орбита

ϑ = ϑ*          ϑ ₁ = ϑ* + τ⁰(ϑ*)

Δ u (ϑ*)                Δ u ₁

Импульсы программы встречи связаны с импульсами оптимального межорбитального перелета:

Δ u (ϑ*) + Δ u ₂ = Δ u ₁ ⁰(ϑ*);

Δ u ₁ + V _пр = Δ u ₂ ⁰(ϑ*).

Определим    Δ u (ϑ*) = (1 – k )Δ u ₁ ⁰(ϑ*);

Δ u ₂ = k Δ u ₁ ⁰(ϑ*); 0 ≤ k ≤ 1. Разность фаз на момент ϑ* = ϑ ₁ – τ⁰(ϑ*) является функцией параметра k деления импульса Δ u ₁ ⁰(ϑ*) и определяется по формуле:

c ₁ (ϑ *) = 3τ⁰(ϑ*)Δ u ₂ ⁰(ϑ*) + 6π V _пр + 6π k Δ u ₁ ⁰(ϑ*). (27)

в момент ϑ ₁ = ϑ + τ⁰(ϑ) касается орбиты ОС. Трехимпульсная программа корректирования на последнем витке продолжительностью ϑ ₃ – ϑ ₁ = 2π определяется разделением единственного импульса межорбитального перелета Δ u ₂ ⁰(ϑ), определяемого по формуле (4) и прикладываемого в точке касания. В этом случае продолжительность перелета с момента ϑ до момента ϑ _пр

T * = ϑ _пр – ϑ = 2π + τ⁰(ϑ),      (25)

и программа (13) является частным случаем программ встречи с разделением двух импульсов оптимального межорбитального перелета. Решение уравнения (25), определяющего смену структуры программы встречи, существует, единственно и далее обозначается ϑ*. Общая структура программы встречи в предположении Δϑ = ϑ ₁ – ϑ* = τ⁰(ϑ*) имеет вид:

ϑ ₂ = 2π + ϑ*          ϑ ₃ = 2π + ϑ ₁

Δ u ₂                  Δ u ₃ = V _пр .

Для определения нижней границы разности фаз на момент ϑ* положим k = 0. Максимальная разность фаз на момент ϑ* соответствует отсутствию торможения ( k = 1) и определяется по формуле (12).

Для значений ϑ ≤ ϑ* в структуру программы встречи включается программа (26) перелета с распределением двух импульсов оптимального межорбитального перелета, определенного для момента ϑ*. Фазирование в новой программе встречи обеспечивается дополнительным импульсом Δ u (ϑ) в момент ϑ < ϑ*.

Программа встречи приобретает вид:

ϑ          ϑ*           ϑ ₁ = ϑ* + τ⁰(ϑ*)

Δ u       Δ u (ϑ*)             Δ u ₁

Характеристики оптимального двух-импульсного перелета τ⁰(ϑ*), Δ u ₁ ⁰(ϑ*), Δ u ₂ ⁰(ϑ*) рассчитываются на момент ϑ* с учетом тормозящего относительное движение импульса Δ u (ϑ). Импульсы Δ u (ϑ*), Δ u ₁ , Δ u ₂ программы встречи (28) определяются через импульсы межорбитального перелета так же, как в программе (26).

Программа (28) определяет разность фаз на момент ее начала ϑ:

c ₁ (ϑ) = 3Δϑ′[ c ₂ (ϑ _N ) – Δ u ] + 3τ⁰(ϑ*)Δ u ₂ ⁰(ϑ*) +

+ 6π V _пр +6π k Δ u ₁ ⁰(ϑ*),           (29)

ϑ ₂ = 2π + ϑ*

ϑ ₃ = 2π + ϑ ₁

Δ u ₂

Δ u ₃ = V _пр .

где Δϑ′ = ϑ* – ϑ. Связь (29) разности фаз с программой (28) содержит два варьируемых параметра — Δ u (ϑ) и k .

Очевидно, что если дополнительный к программе (26) импульс Δ u = 0, то программа (28) при k = 0 определяет одинаковую с программой (26) минимальную разность фаз, обеспечивая непрерывность функции c ₁ ^min(ϑ).

Как и в случае Δϑ ≤ τ⁰(ϑ), будем считать, что минимум разности фаз соответствует максимальному значению импульса Δ u (ϑ), и найдем способ его расчета.

Отметим, что импульс Δ u ^max(ϑ) в программе (13) определен из условия Δ u ₁ ⁰(ϑ ₁ ) = V _пр , где импульс Δ u ₁ ⁰(ϑ ₁ ) оптимального межорбитального перелета рассчитывается с учетом импульса Δ u (ϑ) с моментом приложения ϑ = ϑ ₁ – Δϑ.

Программа (28) обеспечивает минимум характеристической скорости встречи, если после приложения Δ u (ϑ) выполнены ограничения на импульсы оптимального межорбитального перелета:

Δ u ₁ ⁰(ϑ*) ≥ 0 и Δ u ₂ ⁰(ϑ*) ≥ V _пр . (30)

Найдем связь между характеристиками оптимальных межорбитальных перелетов, начинающихся в моменты ϑ* и ϑ ₁ . Пусть относительное движение возмущается импульсом фазирования Δ u (ϑ) в момент ϑ ≤ ϑ*. Представим инвариант относительного движения в моменты ϑ* и ϑ ₁ в следующем виде:

4 B ² – D ² – E ² = 4Δ u ₁ ⁰(ϑ*) y (ϑ*) = = 4Δ u ₁ ⁰(ϑ ₁ ) y (ϑ ₁ ).

Система уравнений для определения характеристик оптимального межорбитального перелета, начинающегося в момент ϑ*, имеет вид:

c ₂ – Δ u ₁ ⁰(ϑ*) – Δ u ₂ ⁰(ϑ*) = 0;

c ₃ + 2Δ u ₁ ⁰(ϑ*) + 2Δ u ₂ ⁰(ϑ*)cosτ⁰(ϑ*) = 0; (32)

c4 + 2Δu20(ϑ*)sinτ0(ϑ*) = 0, где параметры относительного движения c2, c3, c4 заданы на момент ϑ*.

Определим с помощью системы (32)

y (ϑ*) = 2 c ₂ + c ₃ = 2Δ u ₂ ⁰(ϑ*)(1 – cosτ⁰(ϑ*));

y (ϑ ₁ ) = 2 c ₂ + c ₃ cosτ⁰(ϑ*) + c ₄ sinτ⁰(ϑ*) =

= 2 c ₂ – [2Δ u ₁ ⁰(ϑ*)cosτ⁰(ϑ*) + 2Δ u ₂ ⁰(ϑ*)cos²τ⁰(ϑ*)]– –2Δ u ₂ ⁰(ϑ*)sin²τ⁰(ϑ*) = 2Δ u ₁ ⁰(ϑ*)(1 – cosτ⁰(ϑ*)).

Подставляя y (ϑ*) и y (ϑ ₁ ) в выражение (31), получим искомую связь:

Δ u ₁ ⁰(ϑ ₁ ) = Δ u ₂ ⁰(ϑ*),           (33)

справедливую для τ⁰(ϑ*) ≠ 2 k π, k = 0, 1, 2 … .

Из связи (33), очевидно, следует

Δ u ₂ ⁰(ϑ ₁ ) = Δ u ₁ ⁰(ϑ*). (34)

Рассматривая наряду с системой (32) подобную систему уравнений для определения характеристик оптимального межорбитального перелета с началом в момент ϑ ₁ , получим

τ⁰(ϑ*) = 2π – τ⁰(ϑ ₁ ). (35)

Отметим, что связи (33), (34) и (35) получены для ϑ ₁ – ϑ* = τ⁰(ϑ*) и импульса Δ u (ϑ), после приложения которого в момент ϑ < ϑ* орбиты КА остаются непересекающимися. Мы воспользуемся полученными связями для формирования программы (28) и расчета нижней границы оптимального диапазона разности фаз, которую она определяет.

Из формул (33) и (34), в частности, следует, что ограничения (30) для программы (28) равносильны ограничениям (19) для программы (13), и импульс Δ u ^max(ϑ) рассчитывается по формуле (22), где, независимо от распределения импульсов межорбитального перелета, принято Δϑ = ϑ ₁ – ϑ = ϑ _пр – 2π – ϑ.

Далее рассчитываются характеристики Δ u ₁ ⁰(ϑ ₁ ), Δ u ₂ ⁰(ϑ ₁ ), τ⁰(ϑ ₁ ) оптимального межорбитального перелета с началом в момент ϑ ₁ = ϑ _пр – 2π. По формулам (33) и (34) определяются импульсы межорбитального перелета и импульсы программы (28). Наконец, по формуле (35) определяются τ⁰(ϑ*) и момент ϑ* = ϑ ₁ – τ⁰(ϑ*). Нижняя граница оптимальных фаз определяется по формуле (29), где следует положить Δ u = Δ u ^max(ϑ) и k = 0. Отметим, что Δ u ₁ = Δ u ₁ (ϑ ₁ ) = 0.

Когда Δϑ = ϑ ₁ – ϑ = 2π, продолжительность встречи с момента ϑ до момента ϑ _пр составляет два витка

T = ϑ _пр – ϑ = (ϑ _пр – ϑ ₁ ) + Δϑ = 4π, (36) и момент ϑ = ϑ ₁ – 2π определяет очередную смену структуры программы встречи. Программа (28) является частным случаем новой структуры, определяемой через характеристики оптимального межорбитального перелета на момент ϑ = ϑ ₁ – 2π. Программа встречи имеет вид:

ϑ

ϑ* = ϑ + τ⁰(ϑ)     ϑ ₁ = 2π + ϑ    ϑ ₂ = 2π + ϑ*     ϑ ₃ = 4π + ϑ

Δ u (ϑ) Δ u (ϑ*) Δ u ₁

где два импульса межорбитального перелета делятся на пять импульсов программы (37). Уравнения связи имеют вид:

Δ u ₂              Δ u ₃ = V _пр ,

Δ u (ϑ) + Δ u ₁ + V _пр = Δ u ₁ ⁰(ϑ);

Δ u (ϑ*) + Δ u ₂ = Δ u ₂ ⁰(ϑ).

Минимальная фаза отвечает распределению первого импульса межорбитального перелета, полученному в предположении, что импульс торможения определяется по формуле (22), где АЗ = 2п:

А и (З) = А и 0(З) - V _пр ; А и 1 = 0.

Для слагаемых второго импульса межорбитального перелета примем, что

А и (З*) = (1 - к )А и 0(З); А и 2 = к А и 0(З), тогда разность фаз на момент З приложения импульса А и определяется по формуле c 1(З) = 3т0(З)(1 - к)Аи0 +

+ 3(2п + т⁰(З)) к А и 0(З) + 12п V пр.

Минимальная фаза отвечает распределению второго импульса перелета с параметром k = 0 и определяется по формуле c ™(З) = 3т0(З)А и 0(З) + 12п Vпр.

Программа встречи продолжительностью два витка для перелета с нижней границы оптимальных фаз содержит три значащих импульса, поскольку А и ₁ = А и ₂ = 0.

Зависимости нижней c ^I ₁ ⁿⁱⁿ(З) и верхней c ^тах(З) границ диапазона оптимальных разностей фаз представлены на рис. 1 для значений аргумента З1 - 2п С З С З1. Расчет выполнен для коэллиптических орбит с разницей высот 2 c ₂ = 187,5 км. Для представления в градусной мере безразмерная разность фаз умножена на 57,295°.

с,(Э), °

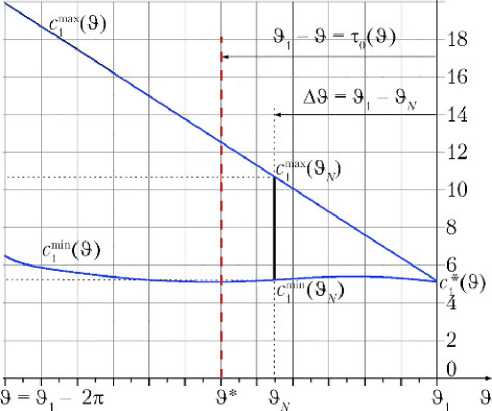
Рис. 1. Границы диапазона оптимальных разностей фаз для аргумента З

Траектории перелета со встречей в орбитальной системе координат (ОСК)

ОС с нижней границы разности фаз для коэллиптических орбиты выведения АК и орбиты ОС представлены на рис. 2.

Параметр траекторий 0 С АЗ С 360°.

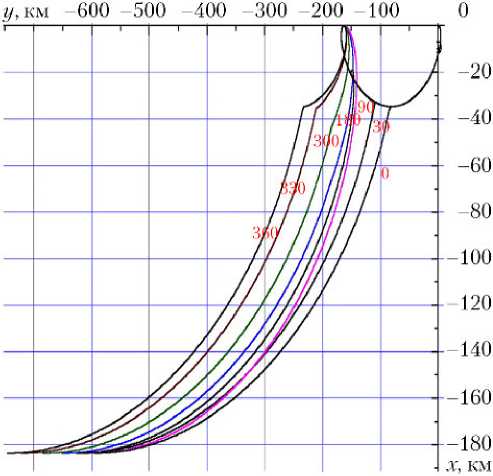
Рис. 2. Траектории встречи с нижней границы разности фаз

определение программы встречидля компланарных орбит как функции АЗ

Минимум характеристической скорости встречи, определяющий минимальные затраты топлива на операцию встречи, достигается, когда разность фаз на фактическое начало маневрирования, т. е. на момент приложения З первого импульса Аи(З) программы встречи, находится в диапазоне оптимальных фаз c 11nin(З) С c 1(З) С c‘^(З),      (38)

где З N С З С З1.

Аналитическая зависимость верхней границы диапазона оптимальных фаз как функция аргумента АЗ определяется формулой (12), где З1 = З _пр - 2п; АЗ = З1 - З. Характеристики оптимального межорбитального перелета т⁰(З1) и А и 0(З1) для невозмущенного относительного движения от момента З N до момента З1 вычисляются по формулам (7), (2) и (3).

Перед расчетом нижней границы необходимо найти единственное решение З* трансцендентного уравнения (25), в предположении невозмущенного относительного движения от момента З N до момента З*. Значение З* определяет момент смены структуры программы, построенной по методу распределения импульсов оптимального межорбитального перелета.

Процедура расчета нижней границы диапазона оптимальных фаз в функции Δϑ определена в предыдущем разделе. Отметим, что максимальное значение фазирующего импульса Δ u ^max(ϑ), замедляющего относительное движение, определяется аргументом Δϑ и не зависит от структуры программы встречи.

Структура программы встречи для заданных на момент начала маневрирования ϑ _N параметров относительного движения определяется значением временного промежутка Δϑ = ϑ ₁ – ϑ _N между моментом ϑ _N приложения фазирующего импульса Δ u (ϑ _N ) и началом ϑ ₁ трехимпульсной программы (6) встречи продолжительностью один виток. В программе (6) разделяется только первый импульс межорбитального перелета.

В случае, когда Δϑ ≤ τ⁰(ϑ _N ), т. е. ϑ _N ≥ ϑ*, для c ₁ (ϑ _N ), удовлетворяющих условию (38), оптимальная программа встречи — четырехимпульсная, структура программы определяется формулами (13), а продолжительность встречи с момента приложения фазирующего импульса Δ T = ϑ ₃ – ϑ _N = 2π + Δϑ.

Расчет программы начинается с определения фазирующего импульса Δ u (ϑ _N ). Разность фаз на момент ϑ ₁ после приложения импульса Δ u (ϑ _N ) определяется по формуле:

c ₁ (ϑ ₁ ) = c ₁ (ϑ _N ) – 3[ c ₂ (ϑ _N ) – Δ u (ϑ _N )](ϑ ₁ – ϑ _N ). (39)

Разность фаз в положении соединения, выраженная через характеристики трехимпульсного маневра с началом в момент ϑ ₁ , являющиеся функциями Δ u (ϑ _N ), определяется по формуле:

c ₁ *(ϑ ₁ ) = 3τ⁰(ϑ ₁ )Δ u ₂ ⁰(ϑ ₁ ) + 6π V _пр . (40)

Трансцендентное уравнение для определения Δ u (ϑ _N ) имеет вид:

c ₁ (ϑ ₁ ) = c ₁ *(ϑ ₁ ). (41)

В процессе итераций определяются значения Δ u ₁ ⁰(ϑ ₁ ), Δ u ₂ ⁰(ϑ ₁ ), τ⁰(ϑ ₁ ), определяющие трехимпульсную программу конечного участка.

На рис. 1 представлены границы диапазона оптимальных фаз для 0 ≤ Δϑ ≤ 2π в функции текущего времени ϑN ≤ ϑ ≤ ϑ1. Вертикальная прямая при значении аргумента ϑ* = ϑ1 – τ0(ϑ*) определяет максимальный диапазон оптимальных фаз для программы (13). Если программа встречи начинается в момент разрешенного начала маневрирования ϑ = ϑN, то область оптимальных фаз представляет отрезок [c1min(ϑN), c1max(ϑN)] на рис. 1. Из любой точки диапазона оптимальных фаз возможен оптимальный перелет со встречей.

В практически важном случае, когда ϑ = ϑ*, в программе встречи вида (26) разделены оба импульса межорбитального перелета, а импульсы программы определяются по формулам:

Δ u = (1 – k )Δ u ₁ ⁰(ϑ);

_{Δ u 1 = Δ u 20(ϑ) – V пр;}

Δ u ₂ = k Δ u ₁ ⁰(ϑ);

Δ u ₃ = V _пр ;

0 ≤ k ≤ 1.

Для заданной разности фаз на момент ϑ = ϑ* из диапазона оптимальных фаз параметр k деления импульса Δ u ₁ ⁰(ϑ) определяется из уравнения связи (27). Следует отметить, что характеристики межорбитального перелета вычисляются через прогнозируемые на момент ϑ параметры невозмущенного относительного движения с момента ϑ _N .

Рассмотрим далее случай ϑ ₁ – ϑ _N > τ⁰(ϑ _N ). Структура программы встречи определяется формулами (28). Усложнение программы встречи, очевидно, связано с увеличением числа импульсов, между которыми распределяются два импульса порождающего программу встречи оптимального межорбитального перелета.

Связь (29) заданной разности фаз c ₁ (ϑ _N ) с импульсами программы (28) содержит два неизвестных параметра, если первый импульс программы прикладывается в момент ϑ _N . Очевидно, при введении начального пассивного участка полета с момента ϑ _N до некоторого момента ϑ, удовлетворяющего системе неравенств:

ϑ ₁ – ϑ ≤ τ⁰(ϑ) c ₁ (ϑ) ≥ c ₁ ^min(ϑ),

возможно определить более простую оптимальную программу встречи с момента ϑ до момента ϑ _пр с единственной коррекцией фазирования. При таком подходе область оптимальных фаз при ϑ _N ≤ ϑ* ограничена снизу красной линией на рис. 3. На момент ϑ _N нижняя граница оптимальных фаз рассчитывается по формуле:

c1(ϑN) = c1min(ϑ*) + 3c2(ϑN)(ϑ* – ϑN), где c1min(ϑ*) определяется по формуле (23).

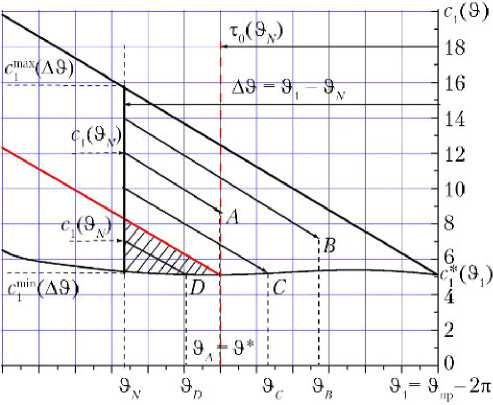
Рис. 3. К построению оптимальной встречи для АЭ >  т ⁰( Э N )

Рассмотрим три типа перелетов со встречей в области (42), отличающихся выбором момента приложения Э фазирующего импульса.

Для перелета типа А Э = Э A = Э*, структура программы имеет вид (26), параметр к деления импульса А и 0(Э*) находится из уравнения (27).

Для перелета типа В Э > Э*, а структура программы имеет вид (13). Выбором момента Э = Э _B — момента реализации фазирующего импульса А и (Э) — можно удовлетворить дополнительные требования. Например, в качестве Э принять момент прохождения узла в случае некомпланарных орбит. Фазирующий импульс А и (Э) определяется как решение трансцендентного уравнения вида (41). В формулах (39) и (40) следует заменить Э N на Э, А и (Э N ) — на А и (Э). Значения А и 0(Э1), А и 20(Э1), т⁰(Э1), определяющие трехимпульс-ную программу продолжительностью один виток на конечном участке встречи, определяются по стандартным формулам.

Для перелета типа С момент приложения фазирующего импульса Э = Э C определяется как решение трансцендентного уравнения c 1(Э) = c ™(Э), (43) где нижняя граница оптимальных фаз c min(d) определяется по формулам (23) и достигается после пассивного полета с момента ЭN до момента Э. Разность фаз на момент Э определяется уравнением c 1(Э) = c 1(Эn) - 3c2(Э - Эn).

Импульс А и ^тах(Э) определяется по формуле (22). Программа встречи имеет вид (13) и содержит три ненулевых импульса.

В области фаз, заштрихованной на рис. 3, система неравенств (42) заведомо не выполняется. Для встречи КА можно предложить два типа перелетов.

Первый перелет — типа D , отмеченный на рис. 3, после пассивного полета с момента Э N до некоторого момента Э = Э D выполняется с нижней границы диапазона оптимальных фаз. Момент Э определяется как решение уравнения (43), где c m ⁿ( Э) определяется по формуле (29) при к = 0. Импульс А и ^тах(Э) определяется по формуле (22). Программа встречи (28), начинающаяся на нижней границе диапазона разности фаз, содержит три значащих импульса.

Для второго типа перелетов , предлагаемых к реализации, требование фиксации момента встречи снимается. Перелет включает пассивный участок с момента Э N до момента начала Э1 трехимпульс-ного перелета со встречей. Промежуток пассивного полета АЭ N = Э1 - Э N определяется как решение уравнения (11). Встреча достигается в момент реализации третьего импульса Э ₃ = Э N + АЭ N + 2п.

результаты моделирования

Рассмотрим применение предложенного подхода для реализации сближения российских кораблей с ОС. В качестве исходных орбит примем орбиту выведения корабля с перигеем 180 км и апогеем 220 км и круговую орбиту ОС высотой 400 км (высоты отсчитываются от поверхности шара с радиусом 6 378,136 км). За момент отделения корабля от носителя принят момент прохождения перигея t ₀ = 00 ч 00 мин 00 с 1 января 2019 г. Соответствующее значение аргумента Э ₀ = 0. Плоскости орбит корабля и ОС в момент t ₀ совпадают. Разрешенное начало маневрирования t _N = t ₀ . В качестве момента встречи принят момент t _пр = 03 ч 00 мин 00 с. Значения аргумента Э определяются по формуле Э = ю ₀ t , где ю ₀ = 1,15687 10^-3с^-1. Относительная скорость на момент встречи v ^→ пр = ( V пр, 0, 0), где V пр = 10 м/c.

Границы диапазона оптимальных разностей фаз на момент Э ₀ суть: c ^min(Э ₀ ) = 7,210°; c ^тах(Э ₀ ) = 21,849°. Момент Э* = 0,4906 витка от момента Э ₀ (00 ч 44 мин 24,6 с от момента t ₀ ). На рис. 4 представлены траектории перелетов со встречей различных типов в ОСК ОС. Корабль находится в пассивном полете с момента t ₀ до момента приложения первого импульса. Значащие

(ненулевые) импульсы пронумерованы в порядке их следования, и для всех вариантов фазирующий импульс А и (3) = А и 1.

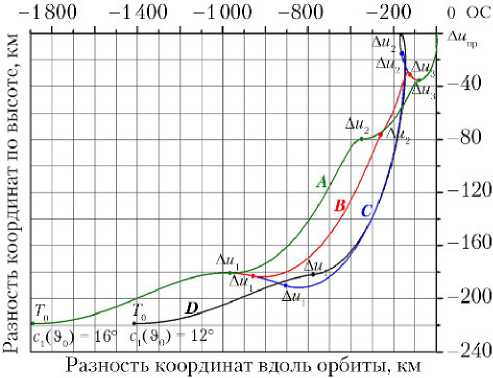
Рис. 4. Траектории перелетов со встречей в орбитальной системе координат орбитальной станции

Для начальной фазы c 1(30) = 16° существуют перелеты типов А , В и С . Траектория перелета типа А , начинающегося в момент 3*, выделена на рис. 4 зеленым цветом. Программа четырехимпульс-ного перелета со встречей приведена в табл. 1.

Таблица 1

Программа встречи для перелета типа А

Время вкл. t , ч:мин:с	00:44:24,6	01:29:28,8	02:14:55,7	03:00:00,0
Время вкл. 3 , витки от 3 0	0,4906	0,9885	1,4906	1,9885
Импульс, м/с	41,844	42,072	21,772	10,0

Траектория перелета типа В , начинающегося в момент времени 3 = 00 ч 50 мин 00 с, показана на рис. 4 красным цветом. Момент начала перелета 3 лежит в диапазоне между 3* и 3 ₁ , разность фаз на момент начала перелета c 1(3) = 7,067° превышает нижнюю границу c mⁱⁿ(3) = 5,192°. Данный перелет четырехимпульсный, программа встречи приведена в табл. 2.

Таблица 2

Программа встречи для перелета типа B

Время вкл. t , ч:мин:с	00:50:00.0	01:29:28,8	02:04:07,6	03:00:00,0
Время вкл. 3 , витки от 3 0	0,5524	0,9885	1,3713	1,9885
Импульс, м/с	44,124	37,159	24,405	10,0

Траектория перелета типа С , начинающегося в момент достижения нижней границы диапазона оптимальных фаз, выделена на рис. 4 синим цветом. Момент начала перелета 3 лежит в диапазоне между 3* и 31, c 1(3) = c mⁱⁿ(3) = 5,625°. Данный перелет трехимпульсный, программа встречи приведена в табл. 3.

Таблица 3

Программа встречи для перелета типа C

Время вкл. t , ч:мин:с	00:58:04,5	01:48:37,0	03:00:00,0
Время вкл. 3 , витки от 3 0	0,6416	1,1999	1,9885
Импульс, м/с	57,754	47,933	10,0

Траектория перелета типа D выделена на рис. 4 черным цветом. Верхняя граница перехода к перелету типа D : c 1^р(3 ₀ ) = 12,957°. Для рассматриваемого варианта начальная разность фаз c 1(30) = 12° находится между границами c mⁱⁿ(3 ₀ ) и c г^р(3 ₀ ). Перелет начинается в момент 3 достижения нижней границы, c 1(3) = c mⁱⁿ(3) = 5,017°. Данный перелет трехимпульсный, программа встречи приведена в табл. 4.

Таблица 4

Программа встречи для перелета типа D

Время вкл. t , ч:мин:с	00:39:05,2	01:21:34,1	03:00:00,0
Время вкл. 3 , витки от 3	0,4318	0,9011	1,9885
Импульс, м/с	62,390	43,298	10,0

выводы

Аппаратура спутниковой навигации, установленная на современных космических кораблях, значительно повысила оперативность и точность навигационного обеспечения системы управления сближением и обеспечила необходимые условия для реализации так называемых схем «быстрой» встречи КА [5]. В статье предложены программы встречи КА для компланарных непересекающихся орбит, дополняющие алгоритм наведения [1, 2] для продолжительностей встречи от одного до двух витков. Определены границы диапазона фаз, в котором характеристическая скорость встречи равна характеристической скорости оптимального межорбитального перелета. Встреча достигается путем реализации трансверсальных импульсов в ОСК корабля. Число импульсов не превышает четырех. Для некомпланарных орбит оптимальные программы корректирования в плоскости опорной орбиты могут дополняться программами корректирования движения по бинормали к орбите, предложенными в работе [2].

Приложение

Линеаризованные дифференциальные уравнения невозмущенного относительного движения двух КА по компланарным орбитам в опорной орбитальной системе координат, вращающейся с угловой скоростью ω ₀ = const, представим в виде [4]:

x" + 2 y ′ = 0;

y" – 2 x ′ – 3 y = 0,

(П1)

где штрихами помечены производные по аргументу ϑ = ω0t. Вектор относительного положения определяется как разность Δr→ = r→П – r→А в проекциях на ОСК, где r→А — вектор положения активного корабля, выполняющего маневры; r→П — вектор положения пассивного корабля, например, орбитальной станции. Аналогично определяется вектор ∆v→ относительной скорости КА. Безразмерный вектор отно- сительного положения

формуле орбиты;

∆ r ^→

, где R ₀ R ₀ безразмерный

∆v→ по формуле R ω .

определяется по — радиус опорной вектор скорости —

Независимая перемен-

ная ϑ в уравнениях движения изменяется непрерывно, монотонно возрастает со временем и является безразмерным аналогом времени, и по отношению к ϑ в статье используется терминология, принятая для реального времени.

Введем новые независимые переменные по формулам:

c ₁ = x – 2 y ′; c ₂ = 2 y + x ′;

1           2               (П2)

c3 = –3y – 2x′; c4 = y′ и представим решение уравнений движения в следующем виде:

c ₁ (ϑ) = c ₁ (ϑ ₀ ) – 3 c ₂ (ϑ – ϑ ₀ );

c ₂ (ϑ) = c ₂ (ϑ ₀ );                                _(П3)

c ₃ (ϑ) = c ₃ (ϑ ₀ )cos(ϑ – ϑ ₀ ) + c ₄ (ϑ ₀ )sin(ϑ – ϑ ₀ );

c ₄ (ϑ) = c ₄ (ϑ ₀ )cos(ϑ – ϑ ₀ ) – c ₃ (ϑ ₀ )sin(ϑ – ϑ⁰).

Физический смысл новых параметров относительного движения поясняется в работах [2, 4]. Параметр c ₁ , называемый в статье разностью фаз КА, является линейным аналогом центрального угла между радиус-векторами КА. Параметр c ₂ — половина разности больших полуосей орбит КА, отнесенная к радиусу круговой опорной орбиты R ₀ . Параметры c ₃ и c ₄ — проекции разности векторов Лапласа на оси орбитальной системы координат.

Относительные координаты и их производные определяются на момент ϑ по формулам:

x = c ₁ + 2 c ₄ ; y = 2 c ₂ + c ₃ ; x ′ = – 3 c ₂ + 2 c ₄ ; y ′ = c ₄ .

(П4)

Для рассматриваемых в статье оптимальных перелетов между непересекающи-мися орбитами КА можно ограничиться рассмотрением только трансверсальных импульсов скорости Δ u _i , возмущающих движение в моменты ϑ _i = ω ₀ t _i , i = 1, 2, …, n . Значения параметров относительного движения до и после приложения импульса определяются по формулам:

c ₁ ⁺ = c ₁ ^–; c ₂ ⁺ = c ₂ ^– – Δ u ;

c ₃ ⁺ = c ₃ ^– + 2Δ u ; c ₄ ⁺ = c ₄ ^–.

(П5)

Систему уравнений, связывающих заданные параметры движения на начало ϑ ₀ и конец ϑ _k перелета и импульсы Δ u _i , необходимые для достижения встречи КА, когда c ₁ (ϑ _k ) = c ₂ (ϑ _k ) = c ₃ (ϑ _k ) = c ₄ (ϑ _k ) = 0, можно представить в виде:

c ₁ (ϑ ₀ ) – Σ ⁿ 3(ϑ _i – ϑ ₀ )Δ u _i = 0;

i = 1

c2(ϑ0) – Σn Δui = 0;(П6)

i = 1

c (ϑ ) + Σ 2Δ u cos(ϑ – ϑ ) = 0;

• 3     0 i = 1 ii

n c (ϑ ) + Σ 2Δu sin(ϑ – ϑ ) = 0.

• 4    0       i = 1        ii

Решением задачи встречи называется программа коррекций, т. е. последовательность импульсов Δ u _i и моментов их приложения ϑ _i , i = 1, 2, …, n , удовлетворяющих системе уравнений (П6).