Переменное нагружение нелинейных пластин и пологих оболочек

гружении исследовано в работе [2] для материалов с различными механическими характеристиками.

В работах [3-5] для решения нелинейных задач теории оболочек используется метод последовательных нагружений, разработанный В.В. Петровым. Было показано, что сходимость процесса решения нелинейных уравнений заметно ухудшается при подходе к значениям критической нагрузки.

В работах [6-8] рассматриваются устойчивость и закритическое поведение геометрически и физически нелинейных задач теории пологих оболочек. Для решения нелинейных уравнений применен метод общей итерации, разработанный М.С. Корнишиным. Метод общей итерации имеет достаточно хорошую сходимость при исследовании докритических, закритических состояний и при определении верхней и нижней критических нагрузок.

В данной работе рассматривается упругопластическое деформирование гибких пластин и пологих оболочек на прямоугольном плане, включая закритические деформации при

Переменном нагружении наружным давлением. Схема нагружения пологой оболочки на прямоугольном плане показана на рис. 1.

При упругопластическом деформировании пластин и пологих оболочек на участке активного нагружения OAN компоненты девиатора напряжений связаны с компонентами девиатора деформаций соотношениями, которые по теории малых упругопластических деформаций имеют вид

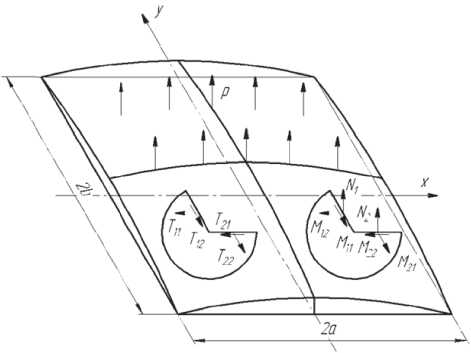
Рис. 1. Пологая оболочка на прямоугольном плане

ра напряжений и деформаций при разгрузке, " j , s j — величины компонентов тензора напряжений и деформаций в конце первого нагружения. Остальные выражения для напряжений и деформаций при разгрузке те же самые, что и при первом нагружении, отмечаются чертой сверху.

Используя общую теорему об упругопластической разгрузке, сформулированную В.В. Мос-квитиным, запишем связь между компонентами девиатора напряжений и компонентами девиатора деформаций при циклическом нагружени-яв виде[10]

"j ^= З Ksn5y +

n

2 " i

n

3 e_i

nn sij so

" j ^— " 2 "     ^Vi, j =123

E где К = —;------ - модуль объемного сжатия,

3 (1 - 2v)

S11 + S22 + ^3

s ₀ = —---²²---— - средняя деформация,

• i ,    j = 1,2,З .

Здесь введены разности

ij

■(”-1) _ (П n ) T7( n ) = j n-1) _ (n n ) ij         "ij   ’ sij       sij         sij '

i , j = 1,2,З,

(n) (n)

где " ', S: ' — величины компонентов тензора jj напряжений и деформаций при n -ом нагруже-

" 11 + " 22 + " зз

" о =------;------

– среднее напряжение,

( n—1) (n—1)

нии, "  *, S ' — величины компонентов тензора напряжений и деформаций в конце

^^^^м

" 0 = 3 К ^ о - зависимость среднего напряжения от средней деформации.

Зависимость между интенсивностями напряжений и деформаций принимается в виде,предложенном А.А. Ильюшиным

" = 3G (1 — ^) е,

предыдущего ( n — 1 ) -го нагружения.

Аналогично уравнениям теории малых упругопластических деформаций при цикличе-

ском нагружении имеют место следующие соот-

ношения

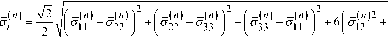
5 ( n ) 2 " 2З

- интенсивность напряжений,

⁽ n )_ V2 I Г ⁽ n )_ ⁽ n ) e i   = _З К ^S 11    ^S 22

где to i = f ( e i ) - функция А.А. Ильюшина.

Переход из упругого состояния в пласти-ческоепринимаем в соответствии с критерием Губера - Мизесапо интенсивности напряжений или деформаций [9]

" = ^ ^ ( " 11 ^— " 22 ) 2 + ( " 22 ^— " зз ) 2 + ( " зз ^— " 11 ) 2 + 6 ( " j², + " 2З + " 1 ) = " _т

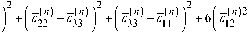
+ ⁽ n ^{) 2 + £} 2З

^8 ⁽ n ) ^{2 + s} 31

- интенсивность деформаций,

о(n ) = "о

5 ^{( n} )₊^( ⁿ L^ ⁿ ) " 11 ⁺ " 22 ⁺ " ЗЗ

– среднее напряжение,

- по интенсивности напряжений, n SH + s22 + S sS } = -^1----22---зз— средняя деформация.

o ₃

Связь между шаровыми составляющими тензора напряжений и тензора деформаций имеет вид

" Оⁿ ) = З К е О” > .

Зависимость интенсивности напряжений от интенсивности деформаций при n - ом нагру-жениипринимает вид

(n)               n)\ -( n)

" i ^; = З О ( 1 — to ^} I e>^},

(n)        (-(n )1

где to 7 = f I e> I - функция А.А. Ильюшина при n - ом нагружении.

В течение полного цикла нагружения внешние силы могут принимать положительные и отрицательные значения. Выражения для компонент напряжений и деформаций при n - ом нагружении примут вид

aj ) = a"-1 + (-1)"-1 aj >, zj ) = Е"4 +(-1)"-1 zj" >, i. j = 1,2,3.

Преобразуем эти формулы,составляя последовательно соотношения, для определения напряжений и деформаций при произвольном ⁿ -ом нагружении через компоненты напряжений и деформаций при первом нагружении a j ) = a+ i ( - 1 ) k ^{- 1} a j ) , k = 2

( " )            "       k - 1 ( " )

^Ei j ~ ^£ij ⁺ i ^{( - 1 ) E} ij ’ i ^, j = ^1,2,3 * k = 2

При исследовании упругопластического деформирования элементов конструкций, в случае циклического нагружения, необходимо учитывать изменение упругопластических свойств материала для каждого цикла нагружения. Должны быть известны диаграммы циклического деформирования для всего процессса многократного нагружения. На рис.2 приведены диаграммы растяжения при первом нагружении OAN , при разгрузке, последующем сжатии и вторичных пластических деформаций NPR и повторном нагружении RST .

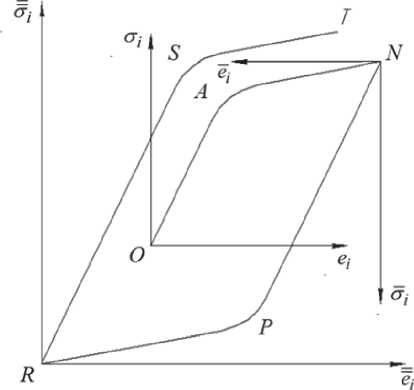
Рис. 2. Диаграммы растяжения при первом нагружении OAN , при разгрузке и последующем сжатии и вторичных пластических деформаций NPR и повторном нагружении RST

В зависимости от законов изменения механических свойств, при циклических нагружениях, различают циклически идеальные материалы у которых упругопластические свойства не зависят от числа циклов нагружения. У цикличе- ски разупрочняемых материалов упругопластические свойства материала уменьшаются, ауци- клически упрочняющихся – увеличиваются.

Если при первом нагружении наступление текучести материала определяется величинами at и £t , то в соответствии с принципом Мазинга при циклическом нагружении наступление текучести определяется величинами От = 2ay и Ет = 2ет. Принцип Мазинга удовлетворительно описывает свойства лишь циклически идеальных материалов. Введя экспериментальный параметр а*, В.В. Москви-тин обобщил принцип Мазинга. В этом случае наступление предела текучести на плоскости

(")          (")

с координатами O i    и Е_;- ' определяется

• - (")

значениями о >т = а * О т по напряжениям и

- (") - eiT = а"еТ по деформациям. Зависимость па

раметра а * от количества циклов нагружения принимаем в виде[9] а * = « 2 ( " - 1 ) ^ , Y <  1 * Постоянные а * и у определяются экспериментально. В случае циклически идеального материала а 2 = 2 , Y = 0 * В случае циклически разу-прочняемого материал а 2 = 2 , Y <  0 , а в случае упрочняемого - а 2 = 2 , Y >  0 .

Рассмотренные соотношения деформационной теории пластичности широко применяются при решении прикладных задач расчета напряженно-деформированного состояния пластин и оболочек при пластических деформациях. Более общими являются соотношения теории течения, которые связывают приращения компонент тензора деформаций с напряжениями и их приращениями, что позволяет описывать сложное нагружение. Деформационная теория строго применима лишь в случае простого нагружения. Однако, деформационная теория обладает относительной простотой исходных соотношений и дает результаты удовлетворительно согласующиеся с экспериментом и при нагружениях отличных от простого[11]. В задачах устойчивости соотношения деформационной теории приводят к меньшим значениям критических нагрузок, причем последние лучше согласуются с экспериментом, чем критические нагрузки, определенные по теории течения [12,13].

При n - ом нагружении компоненты напряжений запишем, выделяя упругую составляющую напряжений, в виде aj )= a'(")+Aaj').i.j = 1,2,3

( " ) _( " - 1 ) ( " ) _У ( " )

где Aaij. = aj -oj - aj дополнительные напряжения, учитывающие отклонения материала от закона Гука, наличие разгрузки и вторичных пластических деформаций.

На основании принятых соотношений для напряжений, опуская индекс « n » можно представить усилия и моменты в сечении оболочки в виде

0 . 5 h

T j = J j = T j + A T,

• - 0. 5 h

• 0 . 5 h

M ij = J ^a y^zdz = M +^ M j , i,j = 1 , 2 , 3

• - 0 . 5 h

N i = N j +^ N i , i = 1 , 2

где T_ij – усилия, действующие в срединной поверхности оболочки, А T .. - добавочные усилия в срединной поверхности, M_ij – изгибающие и крутящий моменты, A M j - добавочные изгибающие моменты и добавочный крутящий момент, N i - поперечные силы, A N - добавочные поперечные силы.

Добавочные силы и моменты учитывают историю нагружения оболочки – напряженноеи деформированное состояние оболочки на предыдущем n -1 -ом нагружении оболочки и нелинейности за счет пластических деформаций.

При повторно переменном нагружении гибких пластин и пологих оболочек давлением, основная система дифференциальных уравнений теории тонких упругопластических оболочек с учетом разгрузки, вторичных пластических деформаций и сжимаемости материала примет вид

D V ² V ² w + F ( ф ) = L ( w,ф ) + G ( A M ij ) + p,

-1h-V²V²о + N ( w ) = K ( w ) + H ( A T j ) .

Приведенная система дифференциальных уравнений позволяет исследовать напряженно – деформированное состояние при циклическом нагружении гибких упругопластических пластин и пологих оболочек в областях докрити-ческих и закритических деформаций. Решение данных задач возможно при шаговом методе прослеживания процесса нагружения с использованием общих методов итерации.

ВЫВОДЫ

Предложенный метод позволяет проводить исследования напряженногои деформированного состояния при повторно переменном нагружении упругопластических пластин и гибких пологих оболочек при изгибе и закритических деформациях, изготовленных из циклически идеальных, упрочняющихся и разупрочняю-щихся материалов.