Переобучение в машинном обучении: проблемы и решения

V.A. Parasich1, , I.V. Parasich1, , https:/ G.I. Volovich2, , S.G. Nekrasov1,

Переобучение – это широко распространённая проблема в машинном обучении, которая сильно влияет на качество обучения. Основной теорией машинного обучения (и переобучения) на сегодняшний день является теория Вапника – Червоненкиса [1]. Одно из основных положений этой теории – обобщающая способность алгоритма зависит от сложности модели. Рассмотрим, от чего ещё может зависеть переобучение.

Почему у алгоритмов машинного обучения возникает способность правильно работать на данных, которых нет в обучающей выборке, и почему эти алгоритмы оказываются способными к обобщению на те данные, которые не участвовали в процессе обучения и про которые алгоритм ничего не знает? По сути, обобщающая способность является следствием того, что похожие объекты имеют похожие значения признаков. Иначе объекты одного класса могут оказаться произвольно разбросанными по признаковому пространству и обучение будет крайне затруднено. Похожей концепцией является требование низкого variance модели в bias-variance tradeoff [2].

Поэ тому ра с смот ри м да л е е у тверждение о том, что обобщающая способнос ть за в и с и т от у с тойч ив ос ти и с та би льн о с ти призн а к ов , в ход ящ и х в мо д е ль .

а)

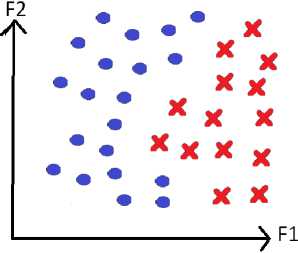
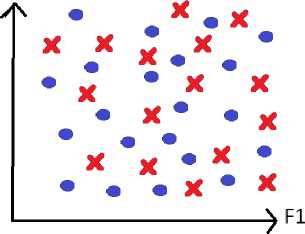
Рис. 1. Пример пространства признаков в случае устойчивых (а) и неустойчивых (b) признаков Fig. 1. An example of a feature space in the case of stable (a) and unstable (b) features

b)

Пред с та в и м д ля на гляд но сти двумерное пространство признаков. Если п ри з н а к и объек тов н е бу д у т об ла д а ть с в ой с тв о м с та бильности, то объекты окажутся раскидан н ыми вперемешку по э тому п ризн а к ов ому п рос тра н ству (рис. 1) и обобщение будет, по сути, нев озможн о, а в озможн о бу д е т тольк о за у чи в а н и е к он к ретных обучающих примеров. Похожей конце п ц и е й яв ляе тс я ги потеза компактности [3, 4].

1.    Эксперимент

Сам ы м и не уст о й ч ивы м и и нестабильными из вычислительных функци й с то чки з р ени я variance я в ляютс я кри птографи че ск и е хэ ш-функции [5] – они построены таким образом, чтобы мал ому и зме н е н и ю в ходно го зн ачения функции соответствовало большое изме н е н и е в ы ход ног о зн аче н и я ( д ля та к ой фу н к ц и и сложно подобрать обратную функцию). По э тому п ров е д ё м с л едующий эксперимент – за меним значения всех признаков модели на знач е н и я к ри п тог ра фи ч еской хэш- ф ун к ц и и от э тих п ризнаков. Для эксперимента был выбран станд артн ый н а б ор д а н н ы х « Ири с ы Ф ише р а » [ 6 ] . В э том наборе данных 150 объектов, для каждого и зв ес тны 4 чи словы х признака – petal_length, p etal _width, sepal_length, sepal_width. Прохэшируем эти признаки (и с п ользов а л с я а лго ри тм sha 256 [7] ) и об у чи м н а н и х SVM (SVC) [8]. В результате признаки пох ожи х о б ъ е к тов п е р е с та л и б ыт ь похожими, а это ключевое условие для того , чтоб ы алгори тм м о г о б об ща тьс я н а д а н ные , которых нет в обучающей выборке. В эксперимент е 105 о б ъ е к тов в к люч е н ы в об у ча ю щ у ю в ыбо рк у , ос та в ш и е с я 4 5 – в тестовую.

С ра в н и м ре зу льта ты о б уче ния на исходных и на модифицированных при зн а к а х. При об у ч ен и и н а и с ходны х п ри з н ак а х качество на обучающей выборке составило 98, 1 %, на тестовой – 97,8 % ( та бл. 1) . При об у че н и и на хэшированных признаках качество на об у ча ю щ ей в ыб ор к е составило 100 %, на тестовой – 26, 7 %, что примерно соответствует качеству случайного угадыван и я. То е с ть п ри об у че н и и н а хэшированных признаках произошло сильно е п е ре о б у че н и е и з -за того, что н а руши лос ь с вой с тв о стабильности признаков (признаки похожих объектов перестали быть похожими).

Таблица 1

Качество классификации SVC на датасете Fisher's Iris в зависимости от используемых признаков

Table 1

The quality of SVC classification on the Fisher's Iris dataset depending on the features used

	Обучение на исходных признаках	Обучение на криптографических хэш-функциях от признаков
К а чес тв о на об у ча ющ е й выб ор к е , %	98,1	100
К а чес тв о на те с т ов ой вы борк е , %	97,8	26,7

Напрашивающийся отсюда вывод: в задачах машинного обучения следует использовать устойчивые признаки с низким variance (то есть те признаки, которые максимально не похожи на криптографические хэш-функции).

Примером неустойчивой функции является деление со знаменателем, близким к нулю. Также неустойчивыми являются операции взятия максимума и минимума, лучше вместо них использовать перцентили. Примером неустойчивого преобразования из области геометрии является восстановление прямой по двум близко лежащим точкам. В этом случае при небольших изменениях в положении точек восстановленная по ним прямая будет изменяться очень сильно.

Другой проблемой являются признаки с очень редкими значениями. Например, если в задаче классификации для некоторого значения V некоторого категориального признака F в обучающей выборке существует только один пример x i с таким значением признака F ( x ) = V (при этом целевая переменная для объекта x 1 принимает значение C ( x i )), то алгоритм может выучить тривиальную закономерность ( F ( x ) = V ) => ( y ( x ) = C ( x i )). В данном случае признак F не является устойчивым с точки зрения variance .

2.    Проблема уверенности (confidence) алгоритма в своих предсказаниях

Часто при использовании моделей машинного обучения возникает необходимость определить уверенность модели в своих предсказаниях. Эту информацию можно использовать, например, для того, чтобы отбрасывать те предсказания, в которых модель не уверена, а учитывать только те, в которых она уверена.

Однако здесь стоит учитывать следующее. Модель, полученная с помощью машинного обучения, как правило, хуже всего работает на тех типах данных, которых не было в обучающей выборке. А раз этих данных не было в обучающей выборке, то у модели при обучении не было возможности правильно настроить выдачу уверенности для таких данных. Поэтому часто возникает проблема излишней уверенности ( overconfidence ) модели в неправильных предсказаниях. На практике определение уверенности алгоритма в его предсказаниях обычно работает также достаточно плохо.

Проблема overconfidence актуальна [9] и для современных больших языковых моделей (LLM), таких как GPT-3 [10] и ChatGPT. ChatGPT, например, иногда пишет правдоподобно звучащие, но неправильные или бессмысленные ответы. При этом сама ChatGPT не может определить, является её ответ правильным или нет, что сильно осложняет её использование в реальных задачах.

3.    Проблема оценки качества работы алгоритма

Причём всё то же самое (что и в случае с уверенностью модели в своих предсказаниях) можно сказать и про измерение качества работы алгоритма на тестовой выборке. Алгоритм хуже всего работает на тех данных, которых не было или было мало в обучающей выборке. А если их не было в обучающей выборке и тестовая выборка взята из того же источника, что и обучающая (например получена с помощью классического случайного разделения одной выборки на две части), то, значит, и в тестовой выборке таких данных не было или было мало.

Это касается в том числе и обучения деревьев решений. Самые проблемные с точки обучения вершины – это те вершины, в которые при обучении попало мало данных (в таких вершинах высок риск переобучения). Но если тестовая выборка взята из того же распределения, что и обучающая, то на этапе тестирования в эти вершины попадёт ещё меньше данных, чем на этапе обучения (так как обучающая выборка обычно в несколько раз больше тестовой). Таким образом, метрики качества работы этих вершин будут ещё более неточными, чем ответы в этих вершинах. Можно бороться с этим с помощью того, что делать тестовую выборку в несколько раз больше обучающей и получать более надёжные оценки качества работы, а потом проводить обучение на полной обучающей выборке, используя подобранные таким образом гиперпараметры. Но тогда гиперпараметры, подобранные при обучении на такой уменьшенной обучающей выборке, могут быть далеки от гиперпараметров, оптимальных для обучения на полноразмерной обучающей выборке.

Поэтому рекомендуется тестировать качество модели не только на тестовых выборках, полученных с помощью случайного train_test_spilt некоторого датасета, но также тестировать Crossdataset Generalization , то есть тестировать качество в том числе на отдельных датасетах, частей которых не было в обучении.

4.    Особенности обучения в высокоразмерных пространствах признаков

Чаще всего в задачах машинного обучения приходится иметь дело с пространствами признаков высокой размерности. При использовании табличных данных у каждого элемента выборки могут быть десятки или сотни признаков. Нейронные сети, применяющиеся в задачах обработки изображений, имеют миллионы параметров, и если использовать число их возможных внутренних состояний в качестве размерности пространства признаков, то и вовсе получится несколько миллионов измерений.

Главной особенность таких пространств является то, что даже при использовании больших обучающих выборок почти всё пространство окажется пустым и не будет заполнено никакими данными. Если мы возьмём пространство размерности 100 и будем рассматривать только его углы (каждый из признаков может иметь по два возможных значения), то получится, что пространство состоит из 2100 точек, что составляет величину порядка 1030. Обучающие выборки, как правило, состоят в лучшем случае из нескольких миллионов элементов. Если же признаков будет не 100, а 1000, то всё становится ещё хуже.

Таким образом, результат работы обученного алгоритма в большинстве точек пространства будет или плохо обусловлен, или вообще являться величиной, зависящей в основном от случайных факторов (рис. 2), потому что в окрестности этих точек нет никаких данных. Также может наблюдаться сильное изменение качества работы алгоритма в ходе обучения, или при небольшом изменении гиперпараметров, или при добавлении небольшого количества данных.

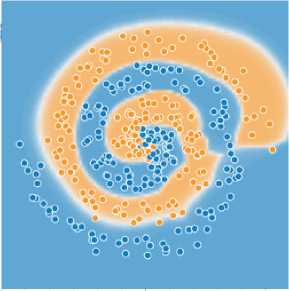
Рис. 2. Примеры разделяющей поверхности обученного алгоритма. В незаполненных областях пространства признаков ответ алгоритма во многом зависит от случайных факторов. В многомерных признаковых пространствах таких незаполненных областей будет гораздо больше

Fig. 2. Examples of the separating surface of the trained algorithm. In unfilled areas of the feature space, the algorithm's response largely depends on random factors. In multidimensional feature spaces, there will be much more such unfilled areas

Один из возможных методов решения данной проблемы – заполнить пустующие области, каким-то образом интерполируя (модифицируя) данные, уже имеющиеся в обучающей выборке. Для задач обработки изображений существуют такие методы, как MixUp [11] и CutMix [12]. Эти методы позволяют повысить качество обучения. При этом полученные изображения могут выглядеть некорректно (то есть в реальности таких изображений никогда не возникает), например, может получиться кошка с головой собаки. Однако лучше настроить ответ алгоритма в этих областях на основании полукорректных данных, чем оставить его полностью случайным. Другим возможным методом для заполнения пустых областей пространства признаков является PseudoLabelling [13].

5.    Влияние неправильного распределения целевой переменнойв обучающей выборке на переобучение

Что такое ошибка на тестовой выборке? Это разница между распределением ответов решающего правила и распределением тестовой выборки в точках, соответствующих элементам тестовой выборки. Однако распределение тестовой выборки не обязательно в точности отражает распределение генеральной совокупности. Некоторые данные в тестовой выборке могут отсутствовать, также может иметь место неправильный баланс классов относительно генеральной сово- купности (во всей выборке либо на определённом участке пространства признаков). То есть может существовать разница в распределениях обучающей и тестовой выборок. Таким образом, ошибка на тестовой выборке состоит из двух слагаемых: разница распределения ответов алгоритма и генеральной совокупности и разница распределения генеральной совокупности и распределения тестовой выборки.

В самом простом случае в тестовой выборке могут быть неправильно сбалансированы классы относительно генеральной совокупности, причём в обучающей выборке они могут быть сбалансированы более правильно, чем в тестовой. В таком случае, подстраивая баланс ответов под баланс тестовой выборки, мы улучшаем качество на тестовой выборке, но ухудшаем качество на генеральной совокупности. При этом на самом деле не происходит повышения обобщающей способности алгоритма, хотя качество на тестовой выборке растёт. Также не является настоящим переобучением обратный случай, когда мы знаем, что в обучающей выборке распределение классов более правильное, чем в тестовой, и двигаем баланс в сторону от тестовой выборки к обучающей (хотя на графиках обучения это будет выглядеть как переобучение – ошибка на обучающей выборке будет уменьшаться, а на тестовой – увеличиваться). Поэтому качество работы алгоритма на тестовой выборке нельзя считать абсолютно точной мерой качества работы алгоритма и его обобщающей способности. Поэтому для повышения надёжности измерения качества рекомендуется применять различные методы кросс-валидации, в том числе k-Fold Cross-Validation [14], а также тестировать Cross-Dataset Generalization .

Для простоты дальнейших рассуждений будем считать, что у нас есть тестовая выборка, точно отражающая генеральную совокупность (хотя в большинстве случаев это недостижимо).

Как говорилось выше, ошибка на тестовой выборке – это разница между распределением ответов модели и распределением тестовой выборки в точках, соответствующих элементам тестовой выборки. Поэтому причиной переобучения может быть не только излишняя сложность модели или нехватка обучающих данных, но и искривление распределения (неправильное распределение) целевой переменной в обучающей выборке (или в определённых участках признакового пространства в обучающей выборке) относительно тестовой выборки (потому что распределение ответов алгоритма, как правило, отражает распределение целевой переменной в обучающей выборке).

Такое искривление может возникнуть, например, из-за недосэмплирования (рис. 3). Из-за особенностей сбора обучающей выборки в некоторой подобласти пространства признаков может не оказаться данных определённого класса, из-за чего обученная модель будет возвращать в этой области пространства признаков неправильный ответ.

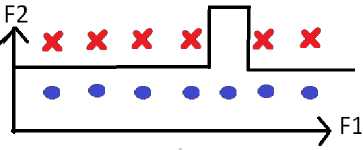
Рис. 3. Пример заучивания ложной закономерности из-за недосэмплирования

Fig. 3. An example of learning a false pattern due to undersampling

Также может возникнуть ситуация пересэмплирования – однотипные (или одинаковые) данные включены в выборку слишком большое число раз, из-за чего сильно искажается распределение в их окрестности. Всё это может негативным образом сказаться на качестве обучения. Примером данной проблемы являются покупки оптовиков в задачах, связанных с предсказанием спроса.

Одним из самых эффективных приёмов улучшения качества обучения является добавление в обучающую выборку сложных обучающих примеров (похожих на те, которые распознаются плохо). Однако при таком добавлении есть большой риск создать искривление распределения в той области, в которую добавляются данные, особенно если мы добавляем примеры только одного класса. Это может привести к тому, что ухудшится качество работы на объектах других классов. При этом может показаться, что это происходит из-за ограниченной ёмкости модели (новые данные «не входят» в модель и поэтому улучшить качество работы на них нельзя). Однако на самом деле стоит просто исправить искривление распределения. Поэтому при добавлении данных в обучающую выборку надо следить за тем, чтобы не создать дополнительных искривлений распределения, при этом не рекомендуется добавлять примеры только одного класса.

При этом в датасетах часто распределение целевой переменной искривлено по тем или иным параметрам. Достаточно сложно обеспечить, чтобы распределение было изначально правильным по всем возможным параметрам. Выравнивание распределения может стать эффективным приёмом повышения качества.

Факторы, влияющие на наблюдаемые признаки объекта, можно разделить на внутренние и внешние (например, условия освещения в задачах обработки изображений). Таким образом, один и тот же объект может оказаться в разных точках пространства признаков в зависимости от внешних условий (разброс этих точек будет зависеть от устойчивости признаков к изменению внешних условий).

При этом, если при изменении внешних условий (например освещения) данные попадают в существенно разные участки пространства признаков, нам надо обеспечить, чтобы в каждом из этих участков пространства признаков распределение целевой переменной было правильным (не возникало искривления распределений). Например, если в задаче классификации собак и кошек (в задаче отличить собаку от кошки) окажется, что в обучающей выборке в условиях очень яркого освещения есть только изображения собак (или их в несколько раз больше, чем изображений кошек), то алгоритм выучит соответствующую ложную закономерность.

Одним из возможных решений данной проблемы может быть нормализация. В случае с разной освещённостью мы можем привести все изображения к одинаковой средней яркости. Тогда данные будут не так сильно разбросаны по разным участкам пространства признаков и будет проще обеспечить правильное распределение целевой переменной во всех случаях (не надо будет отдельно обеспечивать, чтобы было правильное распределение классов и при сильном, и при слабом освещении).

6.    Random Samples Mix-Up

Одна из основных причин переобучения при обучении деревьев решений [15] – при обучении (выборе параметров) некоторых вершин используется малое число обучающих примеров. Так происходит потому, что при обучении каждой вершины множество обучающих данных делится на две части, соответствующие левому и правому сыновьям данной вершины, и далее левый и правый сыновья вершины обучаются на уменьшенных подмножествах оригинального множества данных. Таким образом, при обучении нижних уровней дерева для обучения конкретной вершины используется гораздо меньше данных, чем было в исходном множестве данных или при обучении вершин на верхних уровнях дерева. В лучшем случае при полностью равномерном разделении выборки на две части в каждой из вершин минимальное число примеров для обучения вершины на уровне D будет равно N /2 ^D , где N – размер обучающей выборки, D – глубина вершины. Однако в реальности разделение выборки в каждой из вершин происходит неравномерно, поэтому будут вершины, в которых попадёт ещё меньше данных.

Естественное решение этой проблемы – увеличить число данных, которые используются при обучении вершины. Рассмотрим способы сделать это без расширения обучающей выборки. Мы можем использовать при обучении вершины те обучающие примеры, которые должны были использоваться при обучении других вершин. Чтобы не выделять дополнительную память, мы можем в процессе обучения каждой из вершин для каждого отдельного обучающего примера с некоторой вероятностью p перераспределять его не в ту вершину, в которую он должен был попасть. Легко убедиться, что при такой процедуре у тех вершин, в которых было много данных, будет отобрано много данных, а у тех вершин, в которых было мало данных, будет отобрано мало данных (но в них будет добавлено много данных). То есть произойдёт перераспределение обучающей выборки в пользу тех вершин, в которых было мало данных.

Возможное обобщение данного метода – перемешивать данные между вершинами не случайно, а в зависимости от значений признаков объектов. То есть таким образом, чтобы в другую вершину попадали те объекты, которые имеют более высокую вероятность попасть в эту вершину, если на значения их признаков повлияет шум (или это будет объект, похожий на данный, но с немного другими значениями признаков). Для этого на этапе выбора признака в вершину будем случайно модифицировать значения данного признака для некоторых объектов, вследствие чего часть объектов обучающей выборки в процессе обучения попадёт не в свою вершину.

В наших экспериментах этот метод сам по себе не дал прироста в качестве обучения (хотя это может быть не так в других задачах). Однако если скомбинировать его с базовой версией метода (то есть для половины объектов обучающей выборки использовать базовую схему с полностью случайным перемешиванием объектов, а для другой половины объектов – случайную модификацию признаков), то получится добиться улучшения качества обучения. Результаты экспериментов представлены в табл. 2.

Таблица 2

Качество классификации на тестовой выборке при разных значениях вероятности p m изменения вершины в дереве для обучающего примера

Table 2

The quality of classification on the test sample for different values of the probability p m of changing the node in the tree for training sample

Вероятность изменения вершины для обучающего примера	p m = 0	pm = 0,1	p m = 0,04	p m = 0,02	p m = 0,01	p m = 0,005
Качество классификации случайное перемешивание примеров, %	67,66	68,24	68,39	68,22	67,96	67,82
Качество классификации, случайная модификация признаков, %	67,66	68,15	68.21	68,27	67,85	67,76
Качество классификации, комбинированный алгоритм, %	67,66	68,55	68,78	68,47	68,03	67,95

Выводы

Сформулируем кратко основные выводы.

– Обобщающая способность алгоритма зависит от устойчивости признаков. Похожие объекты должны иметь похожие значения признаков, в противном случае возникает переобучение. Поэтому при решении задач машинного обучения следует использовать устойчивые признаки.

• –    Переобучение также может быть следствием неправильного распределения целевой переменной в пространстве признаков.

• –    При добавлении данных в обучающую выборку важно не создавать искривление распределения целевой переменной в пространстве признаков.

• –    Наличие в выборке большого количества однотипных данных (или данных из одного источника) может привести к искривлению распределения целевой переменной в пространстве признаков и, следовательно, к ухудшению качества обучения.

• –    Устранение неправильного распределения целевой переменной в обучающей выборке может привести к повышению качества.

• –    В многомерных пространствах признаков многие области не заполнены никакими объектами обучающей выборки, поэтому ответ обученного алгоритма в таких областях будет плохо обусловленным или случайным. Поэтому имеет смысл применять аугментации, производящие некорректные изображения (например, MixUp или CutMix), чтобы хоть как-то заполнить пустующие области и сделать ответ алгоритма в них менее случайным.