Перепутывание в двухатомной вырожденной двухфотонной модели

Квантовые перепутанные состояния играют ключевую роль в квантовой теории информации, физике квантовых вычислений, квантовой связи и квантовой криптографии [1]. В последнее время было опубликовано большое количество работ, в которых исследовались свойства перепутанных состояний, их возможные применения в квантовой информатике, а также различные схемы получения перепутанных состояний [2]. Простейшая система, в которой возможна генерация атом-полевых перепутанных состояний, является модель Джейнса-Каммингса, описывающая взаимодействие двухуровневого атома с модой квантового электромагнитного поля в идеальном резонаторе [3]. Модель Джейнса-Каммингса играет фундаментальную роль в квантовой оптике, поскольку позволяет описать все основные квантовые эффекты взаимодействия излучения с веществом. В последнее время атом-полевые перепутанные состояния были получены в экспериментах с одноатомными мазерами [4,5]. Исследования атом-полевых перепутанных состояний в модели Джейнса-Камминса (МДК) и ее простейших обобщениях были инициированы Фениксом и Найтом [6], а также Геа-Банаклоче [7]. Исследуя динамику фон-неймановской редуцированной атомной энтропии, Феникс и Найт впервые показали, что двухуровневый атом, взаимодействующий с модой квантового электромагнитного поля и приготовленный в чистом состоянии, вновь оказывается в чистом состоянии на половине периода затухания осцилляций Раби населенностей атомных уровней, причем в этот момент времени состояния атома и поля распу-

тываются. Аналогичные результаты независимо были получены Геа-Банаклоче при изучении временного поведения атомной линейной энтропии. Результаты Геа-Банаклоче были позднее обобщены на случай одноатомной модели с двухфотонными вырожденными переходами [8] и двухатомной модели с однофотонными [9] и нерожденными двухфотонными переходами [10].

В настоящей работе мы исследуем атом-поле-вое перепутывание для двухатомной вырожденной двухфотонной модели. Рассматриваемая модель описывает взаимодействие двух идентичных двухуровневых атомов с частотой перехода to ₀ , резонансно взаимодействующих с модой квантового электромагнитного поля частоты to = to ₀ 1 2 в идеальном резонаторе посредством вырожденных двухфотонных переходов. Гамильтониан взаимодействия такой модели имеет вид

H int = h E g [ ⁽ a ^{+ )2} Rr + a ² Rt\ (1) i = 1

где a ⁺ ( a ) — оператор рождения (уничтожения) фотона резонаторной моды, R + (R - ) - повышающий (понижающий) оператор в i -ом двухуровневом атоме ( i = 1 , 2 ), g - константа атом-полевого взаимодействия.

Предположим, что атомы в начальный момент времени приготовлены в чистой суперпозиции возбужденных и основного состояний, а поле в когерентном состоянии. Тогда волновая функция системы в начальный момент времен есть

| Т (0) > = (а \ +а + в | +а + Т\ -,+> + 5| -а) I и> (2) где а, в, у и 5 — произвольные комплексные величины, удовлетворяющие условию

I а|2 +|в|2 +\У\2 +|5|2 = 1,

а

| x, У >= | x >| У > (x, У = -,+)

- двухатомные базисные состояния. Здесь | -> - основное, и | +) - возбужденное состояние в одиночном двухуровневом атоме. Начальное состояние поля

X

I ^U > = Е ® п ¹ n >  n = 0

– одномодовое когерентное состояние с коэффициентами to n равными

_   - n1 2

ton = exp(-n/2) "= e'ф , 4 n!

где и = n^1/2e'^ф , n =| и | ² — среднее число фотонов и ф ? фаза когерентного состояния. Точное решение уравнения Шредингера для временной волной функции с начальными условиями (2) имеет вид

I T t ) >= Е ( 4 (t) I +,+>+ B (t ) Ы+ C (t ) I +,->+ D n (t ) I -,+> ) I n >. (3) n

Здесь использованы следующие обозначения:

4 ⁽ t ) = ^{( 2} n J ) ( pn + 9„ ²cos n nt ) a C„ ^- („ qn I n n ⁾⁽sin П nt( P + у ) C„ + 2 ^-

- (4 p„q„ I П " )sin²( n n / 2) t5C „ ,

Bn ⁽ t ) = i qn 1 ⁿ n ^{)sin n} „t^ Cn ■ ( cos² ( ⁿ n / 2) tp - sin - i ⁿ n ri)ty ) Cn + 2 -

4 pn ^{1 n} n Nn ⁿ _nt 5 C_n + 4 ;

4 pn I ⁿ n ^{)sin n} nt ^ Cn + 4 ;

Dn (t) = -(4pnqn IП2 )sin2(n n/2) taC - (./ Пn )sin Пnt (в+у) C +2 + +(2I nn)(qn + p^cos Пnt )5C„+4, где nn = 7p„2+q2, qn = V(n+1)(n+2), p„ = Т(й+з)(й+4).

Используя точное решение (3), мы можем вычислить редуцированную атомную матрицу плотности, усредняя | Т ( t ) >(^ ( t ) | по полевым переменным, и с ее помощью исследовать временное поведение линейной атомной энтропии S = 1 - Tr ( р 4 T ) . Покажем, что для определенных начальных состояний атомной подсистемы в определенные моменты времени полная волновая функция системы распадается на произведение атомной и полевой частей. Для того чтобы получить такой результат предположим, что поле в начальный момент находится в когерентном состоянии с большим средним числом фотонов, и исследуем временное поведение собственных состояний полуклассического гамильтониана взаимодействия. Полуклассический гамильтониан взаимодействия имеет вид

H_SC = h g [ ( и )² Л 1 ^- + и ² Л 1 ⁺ + ( и )² R ₂ ^- + и ² R ₂ ⁺ ] . (4)

Собственные функции полуклассического гамильтониана есть:

|Ф1> = 2[eф | +,+>+| -,->+ e2ф(| +,->+1-,+>)],

| Ф2 >=1 [e4фф | +,+>+1 -,-> -e11ф (| +,->+1 -,+>)],

|Фз>= i[-e4ФН+>+|-,->], |Ф4> = i[|+,->-|-,+>].

Если атомы в начальный момент времени приготовлены в одном из собственных состояний полуклассического гамильтониана, а поле в когерентном состоянии с большой интенсивностью, то волновые функции всей системы имеют следующие асимптотики:

|Ф1>Iи >2 e-^igte4фI +,+>+1-,->+e"iige-2(P(| +,->+ |-,+>)}х

X хЕ Cn|n>e-nn-4t,                    (5)

n = 0

| Ф ₂ > | u > > j( e^ ig e^ i P | +,+>+1 -,->+ e^ ig e" - ^{г ф} ( | +,->-1 -,+> ) } х

X хЕ c„ | n>e^"-4t,                      (6)

n = 0

| Ф3 >|" > Ф >| и, |Ф4 >| и>>|Ф4 >| u>, (7)

Хорошо видно из выражений (5)-(7), что для рассматриваемых начальных состояний атомов и поля волновые векторы системы факторизуются в любой момент времени. Это означает, что в случае, когда атомы приготовлены в одном из собственных состояний полуклассического гамильтониана, состояния атомов и поля не перепутываются с течением времени. При этом для начальных атомных состояний | Ф ₃ >  и |Ф ₄ >  волновая функция всей системы вообще не эволюционирует с течением времени, а для начальных состояний | Ф 1 >  и. | Ф ₂ >  эволюция системы происходит таким образом, что ни в один из моментов времени атомная подсистема не возвращается в исходное состояние. Однако, как видно из формул (5), (6), для выбранных начальных состояний атомные части полных волновых функций точно совпадают для моментов времен

T T

1 1 = (4 k + 1)-^^L , 1 2 = (4 k + 3)-^ R , (8) где k – целое число, а T_R – большой периодов восстановления осцилляций Раби населенностей атомных уровней для двухатомной вырожденной двухфотонной модели. Заметим, что для указанной модели имеются два периода восстановления осцилляций Раби, определяемые условиями:

|n+1 -n„|TR = 2^k, и |2Ц, +1 -2Ц,|Т'R=2nk.(9)

Для интенсивного когерентного поля " □ 1 из (9) имеем, что TR = п/g и T'R = П2g . Для рассматриваемой модели в результате имеются две серии моментов времени, в которые атомная подсистема, приготовленная первоначально в состояниях | Ф1> или | Ф 2>, оказывается в одном и том же чистом состоянии:

2{-e4i

—e2iV (|+,->+|-,+>)}.

Таким образом, полное распутывание атомной и полевой подсистем для рассматриваемой модели имеет место в моменты времени t ₁ и t ₂ только в том случае, если атомная система первоначально приготовлена в виде линейной суперпозиции состояний | Ф 1 >  и | Ф ₂ > . Обозначим такие атомные состояния как

1 ^ = 72 (|+’">+| —’+>)= ‘"'"2 (|Ф1>—|Ф2 >) (10) и

। ^ = 2 (e4 Р|+-+>+|—’—>)= 72 (|Ф1>+|Ф2>)-(11)

Полученные выше результаты отличаются от тех, что были найдены ранее для времен распутывания двухатомной однофотонной модели [8] и одноатомной вырожденной двухфотонной модели [7]. В первом случае времена распутывания составляют половину периода восстановления осцилляций Раби для состояний типа (10), (11). Для вырожденной двухфотонной одноатомной модели времена распутывания составляют 1/4 и 3/4 от периода восстановления осцилляций Раби атомных населенностей, причем независимо от выбора начального атомного состояния.

Значения времен атом-полевого распутывания, полученные на основе анализа асимптотического поведения вектора состояния, могут быть проверены путем численного моделирования редуцированной атомной энтропии исследуемой системы. В случае двухатомной модели линейная атомная энтропия S = 0 для полностью распутанного состояния атомов и поля и S=3/4 для макси-

Кроме того, полевые части волновых функций (5) и (6) точно совпадают в случае

е ' ^ n - 4 t _ е - ^ n - 4 t

мально запутанного атом-полевого состояния.

Результаты численного моделирования ли нейной редуцированной атомной энтропии пред ставлены на рис. 1-2. При этом выбирались раз

-

-

Для интенсивного резонаторного поля n □ 1 соотношение (12) выполняется для времен

13 = krtg.

В результате для начальных атомных состояний системы вида | ^ 1 >  или | ^ ₂ >  имеются три серии времен распутывании состояний атомов и поля. Заметим также, распутывание состояний

атомов и поля имеет место для любого началь ного состояния при выполнении условий:

личные начальные состояния атомов, а среднее число фотонов для когерентного резонаторного поля равнялось n = 30 . На рис.1 показано временное поведение линейной атомной энтропии для начального атомного состояния вида (10). Из рисунка хорошо видно, что в рассматриваемом случае имеют место три серии времен распутывания, полностью описывающиеся формулами

-

| Q n — 4 | Q n - 2

-

-

Q n - 2 1 1 = 2 n k ,         (14)

Qn 11 = 2nk. (15)

(8) и (12), полученными на основе анализа асим птотического поведения волновой функции пол ной системы. В течение одного периода восста

-

-

-

Для интенсивного резонаторного поля n □ уравнения (14) и (15) удовлетворяются для времен новления осцилляций Раби TR распутывание наблюдается в моменты времени, составляющие 1/8, 3/8, 1/2, 5/8 и 7/8 от большого периода ос-

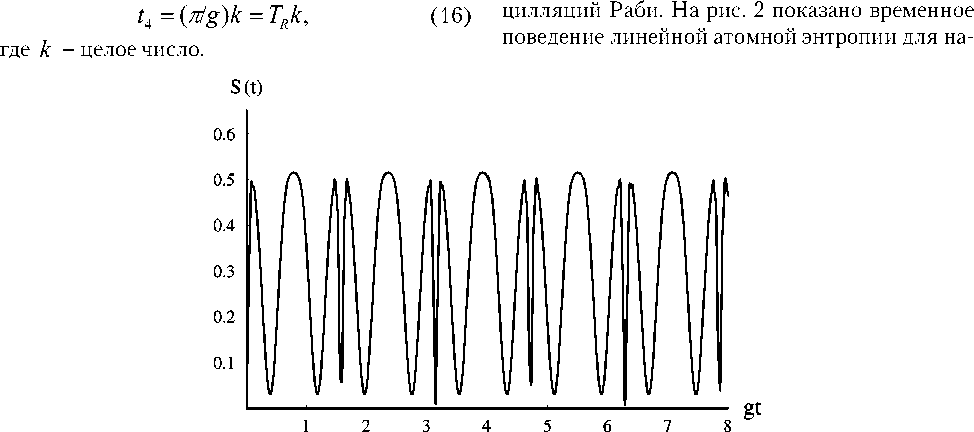
Рис. 1. Временная зависимость линейной атомной энтропии для начального атомного состояния | ^ 1 >  и среднего числа фотонов в резонаторной моде n = 30 .

S(t)

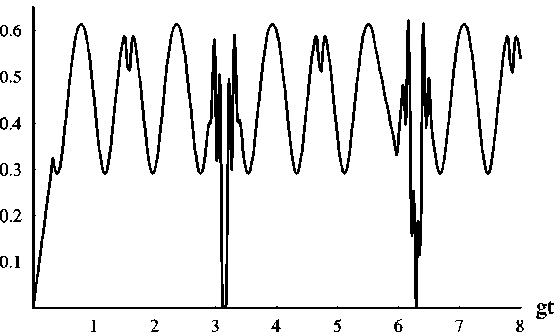
Рис. 2. Временная зависимость линейной атомной энтропии для начального атомного состояния | +, +) и среднего числа фотонов в резонаторной моде n = 30 .

чального атомного состояния вида | +, +) . В этом случае, как и предсказывалось формулой (16) имеется всего одна серия времен распутывания.

Таким образом, результаты численного моделирования полностью подтверждают выводы, сделанные выше на основе анализа асимптотического поведения полной временной волновой функции атом-полевой системы. При этом полученные в работе результаты не являются тривиальным обобщением результатов для двухатомной модели с однофотонными переходами и одноатомной двухфотонной модели.