Performance Comparison of Kalman Filter and Mean Shift Algorithm for Object Tracking

Published Online November 2013 in MECS DOI: 10.5815/ijieeb.2013.05.03

Object tracking has received considerable attention since several years [1,2]. With a general view, it is a combination of computer image processing, video image processing, pattern recognition, artificial intelligence and machine control, and so many related fields of knowledge. All these are put together to detect moving target/targets from obtained images (those may have been extracted from a video), position the target, analyze the characteristics of the location and execute real-time tracking, though the detailed sequence of these sub-operations may be different for different algorithms. The following diagram gives an idea about what methods have been in use to serve the purpose of object tracking based on the type of object tracking that they are capable of [3].

TABLE 1. Object tracking categories

Categories	Representative Work
Point Tracking
• Deterministic methods	MGE tracker, GOA tracker.
• Statistical methods	Kalman filter, JPDAF, PMHT.
Kernel Tracking
• Template and density based appearance models	Mean-shift, KLT, Layering
•    Multi-view appearance models	Eigentracking, SVM tracker.
Silhouette Tracking
• Contour evolution	State space models Variational methods, Heuristic methods.
• Matching shapes	Hausdorff, Hough transform, Histogram.

In this paper, the methods followed for object tracking and subsequently compared, are Kalman filter approach (type of point tracking) and Mean Shift Algorithm (type of kernel tracking). Firstly, the mathematical models suitable for both the algorithms are formulated; then, various performance parameters of the algorithms are evaluated based on simulation results; at last, evaluation results of the comparative study of both the algorithms are summarized and presented.

• II.  PROBLEM FORMULATION

The tracking problem considered in this paper assumes motion of an object on a plane. Threedimensional motion can be handled through repeated use of the two-dimensional system. The problem can be viewed either as an object moving with respect to a sensor or the converse; the two situations are handled through a simple coordinate transformation [4].

Tracking objects can be complex due to [3]:

—loss of information caused by projection of the 3D world on a 2D image,

—noise in images,

—complex object motion,

—non-rigid or articulated nature of objects,

—partial and full object occlusions,

—complex object shapes,

—scene illumination changes, and

—real-time processing requirements.

In real time, calculation of true spatial coordinates of an object (identified by a set of pixels in the field of image processing) by any device is not possible due to the challenges mentioned above. Hence, the need of estimation techniques, two of which, broadly used are those using Kalman filter and Mean Shift algorithm respectively.

This paper is based on a comparative study of these two estimation techniques. We attempt to compare the flexibility, accuracy, noise performances and time complexity of both the systems by simulation through MATLAB and additional features, wherever considered appropriate.

• III.  MATHEMATICAL MODELINGSTATE

SPACE MODELING OF BALL TRACKING PROBLEM:

A moving object can be recognized from a video sequence by intensity variations of pixels across the images and that can be written in state space form as follows: [5].

x k + 1		p	0	dt	0 ■	Xk		0	0	dt 2 /2	,0	0
Ук + 1	-	0	1	0	dt	yk	+	0	0	0	dt 2/2	0
vx k + 1		0	0	1	0	v k		0	0	dt	0	g x
vx k + 1 ,		[ o	0	0	1 J	_ v y k .		. 0	0	0	dt	. g y

Where xt+1,yt+1 are x,y-coordinates of centre of ball at the instant, vxt+1,vyt+1 are x, y-component of velocity at the instant, xt,yt are x,y-coordinates of centre of ball at previous instant, vxt,vyt are x, y-component of velocity at previous instant, gx , gy are accelerations in x, y –directions.

When the body is moving under gravity, acceleration in y-direction is equal to the acceleration due to gravity and acceleration along x-direction is assumed to be zero. On the other hand, when the body is simply translating, acceleration along y direction is also assumed to be zero. Taking the x and y coordinates of the centroid of the detected object as the elements of the measurement vector, we have, zk = H.xk + vk (2)

Where z k is the measurement vector, and v k ~ (0,R k ), is assumed as zero mean white Gaussian noise with covariance R _k (called measurement noise covariance). Both noises are assumed to be uncorrelated. For this model, the measurement equation will be as follows:

x k + 1

. У к + 1

x k ₊ v k * randn y_k v k * randn

• A.    Kalman filter for object tracking:

Kalman filter is an optimal Recursive Data Processing Algorithm. It consists of the following two phases- (i) prediction and (ii) correction. The first refers to the prediction of the next state using the current set of observations and update the current set of predicted measurements. The second updates the predicted values and gives a much better approximation of the next state. It attempts to achieve a balance between predicted values and noisy measurements. The values of the weights are determined by modeling the state equations.

Kalman filter algorithm can be given as [6]

Pk = A. P. A-1 + Q(4)

Kalman filter working depends on Kalman update given by

Kk = Pk-1. HT (H. Pk-1. HT + R)-1

where, x_c , y_c are centre coordinates of the ball, R=measurement noise covariance, K k =Kalman update, x₀ =initial estimation of the ball.

From the above equation, it is clear that the kalman filter gives more preference to the measurement values, if they are trusted to be nearer to the actual values or else, to the estimated values.

P k + i = 1 - K k . H . P k                      (7)

Measurement covariance matrix is given by

R = E ( v_kv_k ) T                           (8)

V k = standard deviation of measurement noise.

These equations clearly indicate that the kalman gain depends on process noise covariance(R). This kalman gain, in turn alters the predicted position. Hence initialization of the kalman filter is an important task for a kalman filter designer.

• B.    Mean shift algorithm for object tracking:

Moving objects are characterized by their colorhistograms. The key operation of this object tracking algorithm is histogram estimation. It finds the largest degree of similarity between color histogram of the object in current frame with that of the target. Primary mean shift algorithm, based on color feature only, gives an accurate performance especially under partial occlusions [7]. The aim is to maximize the correlation between two histograms. This is done by maximizing the Bhattacharya coefficient. Object tracking from an image frame is performed by a combination of histogram extraction, weight computation and derivation of new location.

As a non-parametric optimization algorithm based on gradient analysis, Mean Shift algorithm was first proposed by Fukunaga and Hostetler [8] and subsequently successfully applied in the field of computer vision [9][10][11][12]. In the mean shift tracking algorithm, the desired object is first selected by an operator or other related methods to show it as a rectangle. Given n data points x i i=1,…,n in the d-dimensional space R^d, the iterative formula of mean shift is as follows:

Exg(|(y, -xi)/b||2) y.+1 =        ----------------г

E g (I⁽ y . ^- x i )/ b l²⁾ i = 1

We can yield y.+1 = y. + ^. d.(10)

Where

\ = he/2 f,, g(y.) > 0, d. =Vfh, k (y.)

fh, k (x) = cry E ((x - x.) h| I2)

nh i = 1

is a multivariate kernel density estimator with profile k which is a Gaussian profile.

fh, g(x)=cgTv Ek (I(x- x.)/ hl I2)

nh . = 1

where c g,d , c k,d are the corresponding normalization constants. We define the derivative as

E x . g ⁽|⁽ x - x i )/ h ||²)

^V m h , g ⁽ x ) = ^J= n—;------------ г ^- x ⁽¹⁴⁾

E g (I⁽ x - x . )/ h ||²⁾

i = 1

Hence, we can yield y.+1 = y. +V mh, g(y.)                    (15)

Where [13]

V m ,,( x ) = ¹ h 2 c fx )           ₍₁6,

• ^{h , g}        2        f ^ˆ h , g ( x )

Above equation shows that the mean shift alternates towards the gradient direction and leads the original point to shift to a local maximum point of the distributing density function. The step size λ t changes along the whole iterative process.

• IV.  EXPERIMENTAL RESULTS

• A.    Sequence characteristics:

The video, taken as input to the tracking system, considered in the paper, has both (a) pure translational motion of a ball followed by (b) motion combining translation and fall under gravity, which will give a proper idea of relative performances of these algorithms, given the nature of motion of the object to be tracked.

The proposed approach is applied to track a moving ball, marked by a circle (in kalman approach) and rectangle (in mean shift approach). The video is converted into frames and the above methods are applied on each frame. All the experiments are in the RGB color space and the video sequences are of 640×480 sizes. The results are obtained in real-time.

• B.    Experimental results on video sequences:

To check if both the algorithms are good enough under different types of motion of the ball i.e.

• 1)    Motion under gravity and translational at the same time, and

• 2)    Only translational motion, a video of a ball translating on one horizontal surface and then falling on to another is taken and both the algorithms are applied after converting the video to frames.

B.A. Motion under gravity and translational at the same time(when the ball translates on an elevated surface and then falls onto ground):

Figure 1 shows some of the frames of the original        find out if both the algorithms stated are successful in video showing the motion of the ball. The aim is to        tracking the ball throughout such a kind of motion.

Figure 1. Motion of the ball

Figure 2. MSA detection of ball

Figure 3. Kalman detection of ball

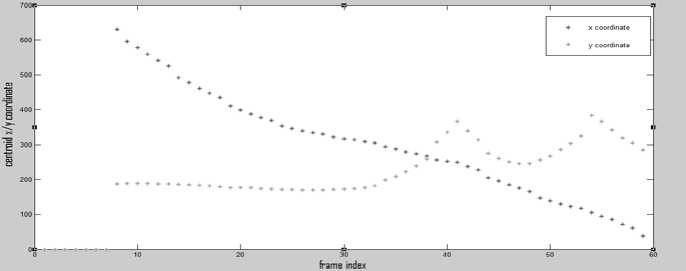
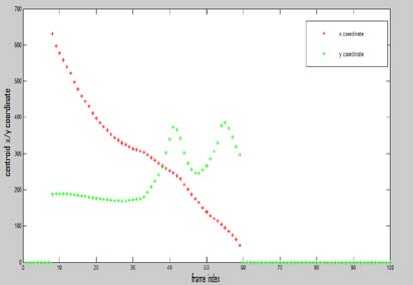
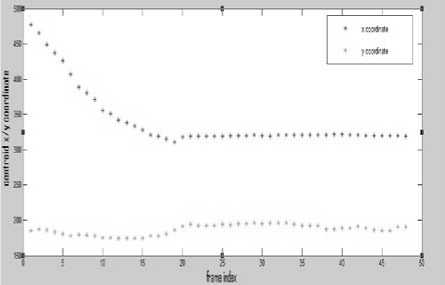
Figure 4. 1)Actual coordinates 2)Kalman estimated coordinates 3)MSA estimated coordinates

Figure 5. Kalman detection of ball under noise

Figure 6. Noisy MSA detection of ball

Figure 7. Motion of the ball (Only translational)

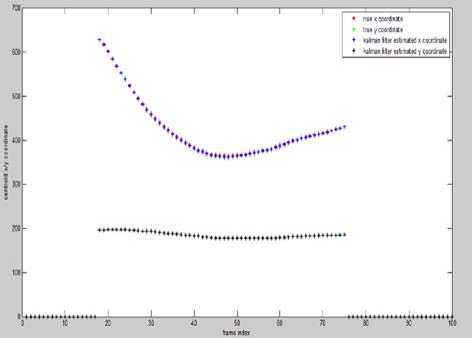
Figure 8. Kalman estimated and true coordinates

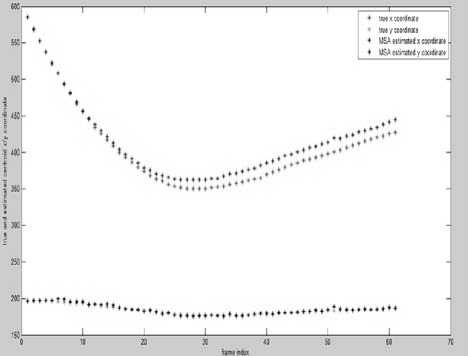
Figure 9. MSA estimated and true coordinates

Figure 2 and Figure 3 indicate the detection and tracking of the ball by kalman filter and mean shift algorithm respectively. In Figure 3 the green circle represents the true outline of the ball and red windows in both the figures indicate the estimated position of the ball. In Figure 4 the graphs indicate the following (with whatever the colors represent, mentioned on the Figure):

• i)       True detection

• ii)      Kalman filter estimation

• iii)      Mean shift algorithm estimation

From the graphs we observe that the mean shift algorithm fails to detect the object once it starts falling under gravitational force.

B.A.A. Noise performance:

The above snapshots (Figure 5,6) are of frames(corrupted with Gaussian noise, that may represent rainy or hazy conditions) having an SNR of ‘3.57’ . As visible from the figures, the kalman filter algorithm works satisfactorily while the mean shift algorithm fails to detect the ball. This is in fact, the minimum SNR requirement for the implemented kalman filter to work. As opposed to this, the minimum SNR required for reasonable performance of the mean shift algorithm is around ‘7.4.’

• B.B.    Only translational motion:

We see that mean shift algorithm fails to track the ball when it falls off from the horizontal surface to ground. So, to compare the required parameters, as done subsequently, we need to have such a case in which both kalman and mean shift algorithm are successful in tracking the ball throughout. As indicated in Figure 7, motion in this case consists only of translational motion of the ball i.e. on a single horizontal surface.

• B.B. A. Computational speed:

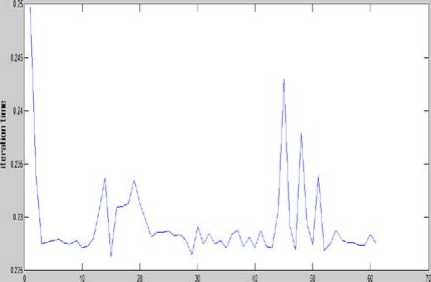
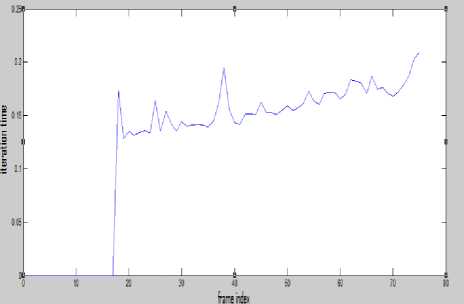
Figure 10 indicates that the iteration time per frame for kalman filter always stays below 0.2s. On the other hand, the iteration time for Mean shift algorithm always is more than 0.2s, as indicated by Figure 11. Hence, it can be concluded that Kalman filter method takes comparatively less time to complete a cycle of execution and thus faster than the Mean Shift algorithm for as much as 100 frames of a video, after which both may be comparable to each other in terms of speed. Thus, kalman filter, on an average, is faster than mean shift algorithm.

B.B.B. Rms error:

It is clearly visible from Table 2 that the kalman filter algorithm accounts for much less mean square error as compared to mean shift algorithm both with respect to estimated x and y coordinates of the centroid of the detected object.

h-i*

Figure 10. MSA iteration time per frame

О 10       20       30       40 SO 60       70

frame index

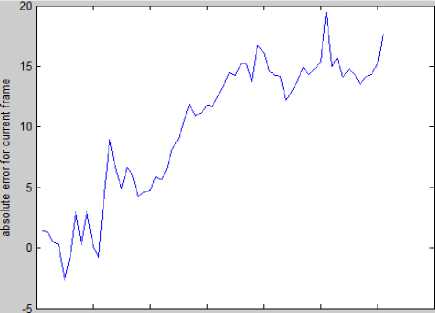
Figure 12. (a) Error of MSA (x coordinate) vs. frame index (Mean=10.14, variance=36.7)

Figure 11. Kalman filter iteration time per frame

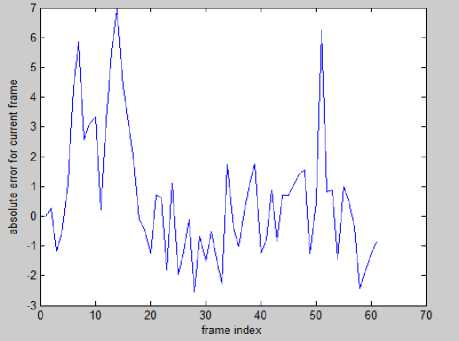
(b)Error of Kalman filter (y coordinate) vs. frame index (Mean=1.8, variance=0.4)

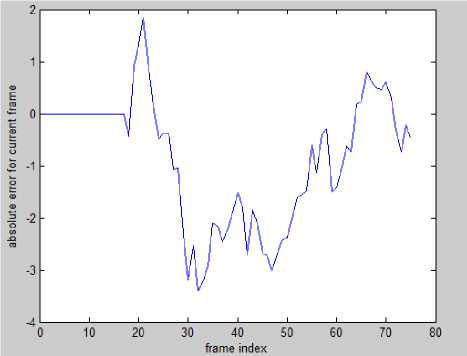
Figure 13. (a) Error of Kalman filter (x coordinate) vs. frame index

(Mean=-0.8, variance=1.5)

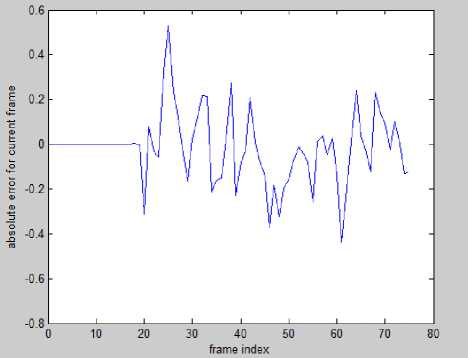
(b) Error of Kalman filter (y coordinate) vs. frame index

(Mean=-0.01, variance=0.025)

TABLE 2. RMS errors

	MSA	Kalman Filter
X-Coordinate	11.9978	1.5099
Y-Coordinate	1.4886	0.1580

Figures 12 and 13 are plots of errors incurred for each frame index for Mean Shift Algorithm and Kalman filter respectively. These are obtained directly by subtracting the true value of corresponding coordinate from the estimated coordinate of detected object in each frame. Means and variances of these errors are mentioned at the figure names, which show that mean shift algorithm accounts for more absolute error compared to kalman filter.

• V. CONCLUSIONS:

With each simulation result, the following conclusions are drawn regarding the relative performances of kalman filter and mean shift algorithms:

• -    The Mean shift algorithm fails to perform when the object is under any kind of motion other than pure translational motion, while the kalman filter is observed to be much more flexible in this regard. - The Kalman filter performs much better than Mean shift algorithm under noisy atmospheric conditions e.g. rainy          ,hazy          condition          etc.

• -    Even when only translational motion is taken into account, the kalman filter results in much lower RMS error and is much faster initially, as compared to Mean shift algorithm.