Performance Comparison of Watermarking Using SVD with Orthogonal Transforms and Their Wavelet Transforms

Автор: H. B. Kekre, Tanuja Sarode, Shachi Natu

Журнал: International Journal of Image, Graphics and Signal Processing(IJIGSP) @ijigsp

Статья в выпуске: 4 vol.7, 2015 года.

Бесплатный доступ

A hybrid watermarking technique using Singular value Decomposition with orthogonal transforms like DCT, Haar, Walsh, Real Fourier Transform and Kekre transform is proposed in this paper. Later, SVD is combined with wavelet transforms generated from these orthogonal transforms. Singular values of watermark are embedded in middle frequency band of column/row transform of host image. Before embedding, Singular values are scaled with suitable scaling factor and are sorted. Column/row transform reduces the computational complexity to half and properties of singular value decomposition and transforms add to robustness. Behaviour of proposed method is evaluated against various attacks like compression, cropping, resizing, and noise addition. For majority of attacks wavelet transforms prove to be more robust than corresponding orthogonal transform from which it is generated.

Еще

Watermarking, Singular value Decomposition, wavelet transform, Kekre transform, Real Fourier Transform

Короткий адрес: https://sciup.org/15013547

IDR: 15013547

Текст научной статьи Performance Comparison of Watermarking Using SVD with Orthogonal Transforms and Their Wavelet Transforms

Published Online March 2015 in MECS DOI: 10.5815/ijigsp.2015.04.01

In today’s digital era, use of internet to disseminate digital images and other multimedia contents is inevitable. This imposes an immense need of security of digital contents transmitted over network. Availability of various tools and techniques allows easy manipulation of digital contents. To protect the digital contents from such undesirable alterations was the motivation for watermarking techniques. Though cryptographic techniques are there to provide security to digital contents, they don’t contribute in protecting copyright of content owner. Watermarking techniques are explicitly meant for protecting the identity of owner of digital contents so that no one else can claim the ownership and can alter the contents.

While using Discrete Wavelet Transform, selection of appropriate frequency band plays an important role as it affects robustness and imperceptibility. Low frequency bands are normally major information contents of an image. Any modification to low frequency components therefore causes degradation into host image which is easily perceptible to Human Visual System [13]. However, in literature many methods of watermarking have been proposed which embed watermark in lower frequency components without losing imperceptibility of watermarked image. High frequency components in an image carry minimal information contents but they are responsible for edges in image. Since they carry minimum information about an image, alteration of these components due to embedding watermark is not easily sensed by human visual system. But it leads to high susceptibility to attacks like lossy image compression which eliminates high frequency components from image [13]. However it may prove more robust to other image processing attacks. To eliminate drawbacks of altering low frequency and high frequency components and to achieve benefits in terms of imperceptibility, selection of mid-frequency components is getting more attention in watermark embedding.

Remaining paper is organized as follows. Section II gives review of existing watermarking techniques in brief. Section III briefly introduces wavelet transforms and singular value decomposition. Section IV describes proposed method in detail. Discussion regarding various attacks performed on watermarked images and response of proposed method to these attacks is given in section V. Section VI compares performance of different column and row wavelet transforms separately. Section VII ends the paper with conclusion.

II. R eview of literature

In literature, various approaches have been tried out for digital watermarking using wavelet transform and singular value decomposition. Veysel Atlantas, A Latif Dogan, Serkan Ozturk [1] proposed a DWT-SVD based watermarking scheme using Particle Swarm Optimizer (PSO). Singular values of each sub-band of cover image are modified by different scaling factors. Modifications were further optimized using PSO to obtain highest possible robustness. Yang Qianli and Cai Yanhong [2] have proposed a DWT-DCT based watermarking wherein image is decomposed into its wavelet coefficients up to three levels. DCT of these coefficients is taken. Watermarking components are also transformed into DCT coefficients and then embedded into DCT coefficients of wavelet transformed image. Normalized Cross Correlation is used to detect the existence of watermark and PSNR is used to test the quality of watermarked image. In a watermarking method given by Xi-Ping He and Qing-Sheng Zhu [3], the wavelet transform is applied to local sub-blocks of image extracted randomly. Watermark image is then adaptively embedded into part of the sub-band coefficients by computing their statistical characteristics. SVD-DCT based watermarking technique is proposed by Zhen Li, Kim-Hui Yap and Bai-Ying Lei [4]. In this technique first SVD of image blocks is computed. Then first few singular values are selected and DCT is applied to them. High frequency band from this SVD-DCT block is selected for watermark embedding. In [5], Rahim Ansari, Mrutyunjaya M Devanalamath, K. Manikantan, S. Ramachandran, proposed a Digital Watermarking Algorithm using a unique combination of Discrete Wavelet Transform (DWT), Discrete Fourier Transform (DFT) and Singular Value Decomposition (SVD) for secured transmission of data through watermarking digital colour images. The singular values obtained from SVD of DWT and DFT transformed watermark is embedded onto the singular values obtained from SVD of DWT and DFT transformed colour image. Scaling and shift invariance property of DFT, rotation invariance property of SVD and robustness of DWT to compression are used to perform secure transmission of data through watermarking. Zhen Li, Kim-Hui Yap and Bai-Ying Lei have proposed a SVD-DCT based watermarking method in [6]. After applying SVD to the cover image blocks, DCT on the macro block comprised of the first singular values of each image block is taken. Watermark is embedded in the high-frequency band of the SVD-DCT block by imposing a particular relationship between some pseudo-randomly selected pairs of the DCT coefficients. Yan Dejun, Yang Rijing, Li Hongyan, and Zheng Jiangchao in [7] proposed a robust digital image watermarking technique based on Singular Value Decomposition (SVD) and Discrete Wavelet Transform (DWT). Spatial relationship of visually recognizable watermark is scattered using Arnold transform. Further, security is enhanced by performing chaotic encryption using chaotic Logistic Mapping. Host image is decomposed into four frequency bands using wavelet decomposition. LL frequency band is decomposed into non-overlapping 4x4 blocks and SVD is applied to each block. Largest singular value of each block is modified with the help of watermark. Inverse SVD followed by inverse DWT is applied to get watermarked image. Reverse steps are followed to recover the watermark from watermarked image. PSNR and Normalized Cross Correlation (NCC) are the metrics used to measure imperceptibility and robustness of the technique.

III. W avelet transforms and singular value decomposition ( svd )

Instead of using traditional Haar wavelet, wavelet transforms are generated from orthogonal transforms using a new wavelet generation algorithm proposed by Dr. Kekre in [11]. These transforms can be generated using different possible size combinations of orthogonal transforms. Required global or local properties of component transforms can be varied by changing the size of component matrix. The concept can be extended further for generation of hybrid wavelet transforms which are composed of two different orthogonal transforms [15].

In past few years, wavelet transforms and SVD are being widely used for many image processing applications including digital watermarking.

Using singular value decomposition, any real matrix A can be decomposed into a product of three matrices U, S and V as A=USVT, where U and V are orthogonal matrices and S is diagonal matrix. If A is mxn matrix, U is mxm orthonormal matrix whose columns are called as left singular vectors of A and V is nxn orthonormal matrix whose columns are called right singular vectors of A [8].

Some properties of SVD which make it useful in image processing are:

• The singular values are unique for a given matrix.
• The rank of matrix A is equal to its nonzero singular values. In many applications, the singular values of a matrix decrease quickly with increasing rank. This property allows us to reduce the noise or compress the matrix data by eliminating the small singular values or the higher ranks [9].
• The singular values of an image have very good stability i.e. when a small perturbation is added to an image; its singular values don’t change significantly [10].

IV. P roposed method

Orthogonal transforms like DCT, Walsh, Haar, DKT and Real Fourier transform and their wavelets are used. Transform is applied to each plane of host image. Instead of full transform only column or row transform of image is taken. Column transform of image matrix f is given by (1) below where f is image to be transformed, T is transform matrix and F is transformed image.

[F]=[T]*[f](1)

Inverse column transform is given by (2).

f=[T]’*[F](2)

Similarly row transform and inverse row transform are given by (3) and (4) respectively.

[F]=[f]*[T]’(3)

[f]=[F]*[T](4)

Thus column or row transform reduces the number of computations to half of those in full transform.

After taking column transform, tendency of image energy concentration is observed to be towards upper rows and in case of row transform, it is observed to be towards left columns of an image. To achieve invisibility and robustness is the challenge in watermarking as they have trade-off. Thus higher robustness may lead to lower imperceptibility of watermarked image. Hence selection of moderate frequency components is required. In full transform, HL and LH frequency bands can be selected for the purpose. However this is not possible for column and row transform. Thus for column transform, moderate frequency elements are in the middle few rows of an image and for row transform it is in middle columns. Hence proper selection of rows in column transform and proper section of columns in row transform is necessary to achieve higher robustness and imperceptibility. For the proposed method, we tried many different ranges of middle frequency elements and ended with the frequency band from row 101 to 130. Singular value decomposition of watermark is obtained. Due to high energy compaction in SVD, we can choose only first few singular values to embed the watermark. This reduces the payload of information to be embedded and also increases imperceptibility. In proposed method first 30 singular values are selected. These values correspond to 99.1944% of watermark energy embedded in host. The middle frequency band elements of host are sorted in descending order. Singular values are scaled down and embedded in such a way that first two values are placed at the positions where energy gap between these values and corresponding frequency elements of host is the minimum. Remaining singular values are placed in consecutive positions after the position of second singular value in host. Scaling factor selection is done adaptively so that first singular value to be embedded maps exactly to highest middle frequency element from the selected band. Inverse column/ row transform of host after substituting singular values yields watermarked image.

Extraction is followed by reversing the steps of embedding. Here first column/ row transform of watermarked image is obtained. From this transformed image middle frequency elements are extracted from the positions where they were embedded. These elements contain the watermark in the form of scaled down singular values. Extracted elements are scaled up and are used to reconstruct the watermark. Quality of recovered watermark is compared with that of embedded watermark by calculating mean absolute pixel difference or Mean Absolute Error between them. Also quality of watermarked image is compared with quality of host image by calculating MAE between the two.

Fig. 1 shows the set of host images and watermark used for experimental work.

(a) Lena (b) Mandrill (c) Peppers (d) Face (e) Puppy (f) NMIMS

Fig. 1. (a)-(e) 256x256 size host images, (f) 128x128 size watermark used for experimental work.

In the proposed watermarking technique, wavelet transforms are generated from corresponding orthogonal transforms using Kekre’s wavelet generation algorithm proposed in [11]. Since we need 256x256 size transform matrix for host, according to the algorithm in [11], we can have following combinations of component orthogonal transforms: (128,2), (64,4), (32,8), (16,16), (8,32), (4,64), (2,128) to generate required size transform matrix. For the proposed work the combinations selected for generation of wavelet transform are (64, 4), (32, 8), (16, 16), (8, 32), (4, 64).

V. P erformance of proposed technique against VARIOUS ATTACKS

To verify the robustness of proposed watermarking technique, watermarked images are subjected to attacks like compression, cropping, noise addition, resizing and histogram equalization. MAE between the embedded watermark and watermark extracted from attacked image measures the robustness. In following subsections each of the attack with variations into it and their results are shown. Representative results of each attack are shown using image Lena for DCT and DCT wavelet (column and row version) and performance of each transform is shown in tables by taking average value of MAE of five host images.

A. Compression of watermarked images

2.228 13.616 2.228 11.966

2.305 15.797

2.305

12.538

Since limited bandwidth is to be used efficiently for data transmission, compression of data with minimum or acceptable level of information loss is the trend. It applies to watermarked images as well. Here watermarked images are compressed in three ways (a) using different orthogonal transforms (DCT, DST, Walsh, Haar and DCT wavelet), (b) using JPEG compression and (c) using Vector Quantization.

Results of these compression attacks are shown in Fig. 2. For each recovered watermark image MAE and for each wavelet transforms (column and row) the combination of component transform which gives minimum MAE is mentioned below the image.

Result images for Compression using Walsh are shown in Fig. 2 below.

DCT column transform

DCT wavelet column transform (4,64)

DCT row transform

DCT wavelet row transform (4,64)

Fig. 2. result images for compression using Walsh transform when DCT column, DCT wavelet column, DCT row and DCT wavelet row transform is used to embed watermark

From Fig. 2 it can be seen that, DCT wavelet transform obtained from (4, 64) combination of component transforms (DCT) gives better quality of recovered watermark than DCT. It has been observed that for other transform based compressions except using DCT, DCT wavelet is better in robustness than DCT. Table 1 below summarizes the results of transform based compression attack for DCT and DCT wavelet transform.

Table 1. MAE between embedded and extracted watermark against transform based compression attack when DCT column and DCT wavelet column transform are used for embedding

Transform used for compression Attack	DCT column transform	DCT wavelet column transform combinations
		(16,16)	(32,8)	(8,32)	(64,4)	(4,64)
DCT	0.000	6.958	9.875	5.150	12.661	3.310
DST	0.516	6.928	9.772	5.135	12.941	3.299
Walsh	13.616	16.840	22.600	12.630	17.373	11.966
Haar	45.764	36.397	17.214	49.284	17.114	17.821
DCT wavelet	58.686	0.000	31.713	50.222	34.372	42.518

From Table 1, it is clear that MAE between embedded and extracted watermark given by column DCT wavelet for Haar and DCT wavelet based compression are far better than column DCT. For other transforms used for compression, DCT wavelet gives acceptable MAE values.

The smallest MAE values given by column DCT wavelet are highlighted.

Table 2 shows MAE values between embedded and extracted watermark for transform based compression attack using DCT row and DCT wavelet row transform for embedding.

Table 2. MAE between embedded and extracted watermark against transform based compression attack when DCT row and DCT wavelet row transform are used for embedding

Transform used for compression Attack	DCT row transform	DCT wavelet row transform combinations
		(16,16)	(32,8)	(8,32)	(64,4)	(4,64)
DCT	0.000	6.485	9.029	4.637	12.259	2.960
DST	0.509	6.509	8.999	4.655	12.695	3.035
Walsh	15.797	16.707	20.532	13.574	15.259	12.528
Haar	50.709	27.361	32.886	24.698	20.792	33.989
DCT wavelet	70.760	0.000	26.201	28.597	27.538	51.150

From Table 2, it is observed that use of DCT wavelet row transform for embedding watermark shows significant performance improvement for compression using Haar and DCT wavelet over row DCT used for embedding.

Fig. 3 shows the watermark extracted using DCT column and DCT wavelet column from VQ compression attack.

DCT column transform

2.493

№1[Ж

University |

DCT wavelet column transform (32,8)

DCT row transform

DCT wavelet row transform (64,4)

62.481

2.957

47.291

2.958

40.150

2.497

72.610

Fig. 3. Result images for VQ compression attack when DCT column and DCT wavelet column transform

From Fig. 3, it can be observed that wavelet transform (column or row version) gives better robustness than its component orthogonal transform for compression attack using Vector Quantization. Similar observations are noted for JPEG compression attack also. MAE values between embedded and extracted watermark obtained for VQ compression and JPEG compression using DCT column transform and various combinations of DCT wavelet column transform are shown in Table 3. Minimum values given by wavelet transform combination are highlighted.

Table 3. MAE between embedded and extracted watermark against VQ based compression and JPEG compression using DCT column transform and DCT wavelet column transform

Type of compression Attack	DCT column transform	DCT wavelet column transform combinations
		(16,16)	(32,8)	(8,32)	(64,4)	(4,64)
Vector Quantization	62.481	58.214	47.291	61.245	47.701	59.080
JPEG compression	83.452	69.599	64.548	67.406	60.624	73.487

Table 4 gives the MAE values between embedded and compression attack using row versions of DCT and DCT extracted watermark for VQ compression and JPEG wavelet.

Table 4. MAE between embedded and extracted watermark against VQ based compression and JPEG compression using DCT row transform and DCT wavelet row transform

Type of compression Attack	DCT row transform	DCT wavelet row transform combinations
		(16,16)	(32,8)	(8,32)	(64,4)	(4,64)
Vector Quantization	72.610	59.801	49.102	61.160	40.150	62.164
JPEG compression	84.252	69.099	69.111	71.109	62.629	76.094

Behavior of other column transforms namely Haar, Walsh, Kekre transform and Real Fourier transform and their wavelet transforms against compression attack is shown in Table 5 to Table 8. Cells highlighted in yellow color represent the minimum MAE obtained by wavelet transform. Cells highlighted in blue color represent that orthogonal transform gives smaller error than wavelet transform. However, such occurrences are very less as can be seen from Table 5 to Table 8. Hence we can conclude that column wavelet transforms are more robust than respective column orthogonal transforms against compression attack performed in various ways.

Table 5. MAE between embedded and extracted watermark against compression using Haar column transform and Haar wavelet column transform

Compression using	Haar wavelet column transform					Column Haar
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Haar
DCT	2.742	4.283	2.786	4.036	3.206	3.480
DST	2.881	4.288	2.878	3.825	3.438	4.054
Walsh	3.557	4.855	2.682	8.337	4.291	8.429
M Haar	0.000	0.000	0.000	0.000	0.000	0.000
JPEG	58.148	56.804	58.843	59.828	57.946	61.223
VQ compression	39.260	40.194	41.140	50.400	45.926	48.788
DCT wavelet	44.043	47.070	43.458	43.511	45.817	44.373

Table 6. MAE between embedded and extracted watermark against compression using Walsh column transform and Walsh wavelet column transform

Compression using	Walsh wavelet column transform					Column Walsh
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Walsh
DCT	1.652	2.566	1.440	1.886	1.886	1.377
DST	1.700	2.877	1.497	2.025	2.025	1.458
Walsh	0.000	4.215	0.000	1.405	1.405	0.000
M Haar	0.000	0.000	0.000	0.000	0.000	7.084
JPEG	63.002	62.112	63.491	62.868	62.868	71.660
VQ compression	45.656	47.222	54.683	49.187	49.187	60.031
DCT wavelet	54.575	54.575	56.897	55.349	55.349	60.842

Table 7. MAE between embedded and extracted watermark against compression using Kekre column transform and Kekre wavelet column transform

Compression using	Kekre wavelet column transform					Column Kekre Transform
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Kekre Transform
DCT	18.340	24.493	20.414	23.056	19.610	20.432
DST	18.223	24.534	20.576	23.284	19.641	20.388
Walsh	26.654	28.812	24.644	32.510	23.614	24.616
M Haar	30.963	34.061	28.771	65.177	31.744	0.000
JPEG	68.723	68.299	67.241	74.670	69.165	67.959
VQ compression	44.388	44.104	41.094	58.687	43.924	42.036
DCT wavelet	64.838	72.287	63.436	75.914	62.735	20.065

Table 8. MAE between embedded and extracted watermark against compression using Real Fourier column transform and Real Fourier wavelet column transform

Compression using	Real Fourier wavelet column transform					Column Real Fourier Transform
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Real Fourier Transform
DCT	5.495	6.046	3.672	6.980	5.548	0.167
DST	5.498	5.912	3.706	7.124	5.560	0.391
Walsh	13.917	13.082	11.817	11.377	12.548	12.833
M Haar	25.908	10.093	26.150	11.565	18.429	44.482
JPEG	70.272	63.356	71.102	59.835	66.141	78.730
VQ compression	48.977	51.569	55.715	50.642	51.726	62.944
DCT wavelet	21.530	36.379	37.603	40.610	34.031	1.201

Behaviour of orthogonal row transforms and their row form MAE values are given below in Table 9 to Table 13. wavelet transforms against compression attack in the

Table 9. MAE between embedded and extracted watermark against compression, using DCT row transform and DCT wavelet row transform

Compression using	DCT wavelet					Row DCT
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row DCT
DCT	6.485	9.029	4.637	12.259	2.960	0.000
DST	6.509	8.999	4.655	12.695	3.035	0.509
Walsh	16.707	20.532	13.574	15.259	12.528	15.797
M Haar	27.361	32.886	24.698	20.792	33.989	50.709
JPEG	69.099	69.111	71.109	62.629	76.094	84.252
VQ compression	59.801	49.102	61.160	40.150	62.164	72.610
DCT wavelet	0.000	31.713	50.222	34.372	42.518	58.686

Table 10. MAE between embedded and extracted watermark against compression using Haar row transform and Haar wavelet row transform

Compression using	Haar wavelet row transform					Row Haar
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Haar
DCT	2.081	1.941	3.091	1.843	3.376	1.724
DST	2.265	1.865	3.340	1.806	3.464	1.856
Walsh	2.311	1.113	4.284	2.511	2.922	3.212
M Haar	0.000	0.000	0.000	0.000	0.000	0.000
JPEG	59.705	61.015	60.675	62.003	60.250	62.482
VQ compression	39.265	43.542	41.548	40.710	39.806	43.824
DCT wavelet	41.510	42.423	46.681	43.776	47.210	45.078

Table 11. MAE between embedded and extracted watermark against compression using Walsh row transform and Walsh wavelet row transform

Compression using	Walsh wavelet row transform					Row Walsh Transform
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Walsh Transform
DCT	1.282	1.591	1.342	1.215	1.215	1.257
DST	1.393	1.714	1.417	1.270	1.270	1.324
Walsh	0.000	0.000	0.000	0.000	0.000	0.000
M Haar	0.000	0.000	0.000	0.000	0.000	8.651
JPEG	65.212	64.931	65.047	67.027	67.027	69.352
VQ compression	46.601	47.172	57.147	48.981	48.980	60.759
DCT wavelet	58.872	54.589	54.823	58.150	58.15004	56.238

Table 12. MAE between embedded and extracted watermark against compression using Kekre row transform and Kekre wavelet row transform

Compression using	Kekre wavelet row transform					Row Kekre Transform
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Kekre Transform
DCT	19.257	19.532	19.276	25.992	20.752	19.405
DST	19.197	19.332	19.466	26.053	20.781	19.302
Walsh	25.433	27.359	26.464	37.167	25.294	23.658
M Haar	28.777	42.377	26.758	61.405	31.084	0.000
JPEG	70.477	70.738	67.930	71.516	70.081	70.114
VQ compression	44.323	46.939	41.921	47.051	46.289	50.957
DCT wavelet	64.917	67.332	62.254	76.033	65.282	64.260

Table 13. MAE between embedded and extracted watermark against compression using Real Fourier row transform and Real Fourier wavelet row transform

Compression using	Real Fourier wavelet row transform					Row Real Fourier Transform
Compression using	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Real Fourier Transform
DCT	5.247	4.623	3.358	6.193	2.407	0.151
DST	5.272	4.633	3.413	6.452	2.435	0.415
Walsh	13.259	11.291	11.610	9.978	13.155	14.995
M Haar	18.767	10.453	18.915	12.650	24.693	43.129
JPEG	69.039	66.405	70.126	58.758	72.301	83.379
VQ compression	56.274	46.621	58.937	39.180	60.879	63.491
DCT wavelet	22.360	35.989	38.491	30.266	53.169	62.269

B. Cropping of Watermarked Images

Cropping of watermarked images is performed in two ways. First is cropping at corners of image wherein 16x16 size portion is cropped at each corner of an image. To observe the effect of increased amount of cropping, 32x32 size squares are also cropped at four corners of an image. Second way is cropping 32x32 size portion from an image at its center. Extracted watermark from such cropped watermarked images are compared with

embedded watermark by calculating MAE between the two. Result images of column DCT and column DCT wavelet and row DCT and Row DCT wavelet against cropping 16x16 portions at corners are shown in Fig. 4. For each recovered watermark, MAE and wavelet transforms (column and row), the combination of component transform which gives minimum MAE is mentioned below the image.

жиж

University

DCT column transform

2.082

12.483

MMirasi

University

№im

University mms

University

2.082

37.428

2.082

34.397

2.082

1.835

DCT row transform

DCT wavelet row transform (32,8)

DCT wavelet column transform (32,8)

Fig. 4. Result images for cropping 16x16 portions at corners when DCT column, DCT wavelet column, DCT row and DCT wavelet row transform is used to embed watermark

From Fig. 4, improvement in robustness against cropping attack using wavelet transform is clearly noticeable from MAE values. In case of column DCT wavelet and row DCT wavelet transform (32, 8) combination of component DCT matrices gives highest robustness.

Table 14 shows MAE values for extracted watermark from different types of cropping attack when column DCT and column DCT wavelet generated from different combinations of DCT is used for embedding and extraction process.

Table 14. MAE between embedded and extracted watermark against cropping attack using column DCT and column DCT wavelet transform

Cropping type	Column DCT wavelet					Column DCT
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column DCT
16x16 crop	14.470	12.483	13.657	15.214	32.891	37.428
32x32 crop	37.386	25.532	7.581	31.046	56.120	69.534
32x32 crop center	24.271	24.572	24.166	0.000	35.549	62.228

From Table 14, it is observed that column DCT wavelet transform performs far better than column DCT especially for 32x32 cropping done at the center of an image.

Similar observations can be made for row DCT wavelet transform and row DCT against cropping attack from Table 15.

Table 15. MAE between embedded and extracted watermark against cropping attack using row DCT and row DCT wavelet transform.

Cropping type	Row DCT wavelet					Row DCT
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row DCT
16x16 crop	2.692	1.835	25.821	3.059	33.239	34.397
32x32 crop	25.900	16.429	7.011	19.618	63.099	75.321
32x32 crop center	3.441	3.310	21.118	0.000	45.252	56.789

combinations used for wavelet generation are observed to wavelet transform performs exceptionally well overbe giving better MAE values. In all cases, column simple column transform.

Performance of row wavelet and respective orthogonal row transform are compared in Table 20 to Table 23. From Table 20 to Table 23, once again robustness of row

wavelet transform is observed to be significantly better than simple row transform.

Table 16. MAE between embedded and extracted watermark against cropping attack using column Haar and column Haar wavelet transform.

Cropping type	Column Haar wavelet					Column Haar
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Haar
16x16 crop	0.293	2.099	4.459	17.323	1.529	18.060
32x32 crop	19.375	6.737	12.159	24.187	5.606	25.467
32x32 crop center	0.244	1.636	5.816	0.000	3.557	0.000

Table 17. MAE between embedded and extracted watermark against cropping attack using column Walsh and column Walsh wavelet transform

Cropping type	Column Walsh wavelet					Column Walsh
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Walsh
16x16 crop	10.177	14.119	5.418	9.905	9.905	21.832
32x32 crop	26.448	25.957	6.893	19.766	19.766	38.805
32x32 crop center	12.256	6.128	6.534	8.306	8.306	26.087

Table 18. MAE between embedded and extracted watermark against cropping attack using column Kekre transform and column Kekre wavelet transform

Cropping type	Column Kekre wavelet					Column Kekre Transform
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Kekre Transform
16x16 crop	3.955	3.494	29.290	16.105	12.289	19.484
32x32 crop	39.768	6.803	2.115	25.121	199.689	63.456
32x32 crop center	3.316	13.725	97.620	0.000	25.098	126.096

Table 19. MAE between embedded and extracted watermark against cropping attack using column RFT and column RFT wavelet transform

Cropping type	Column RFT wavelet					Column RFT
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column RFT
16x16 crop	11.874	12.660	15.532	14.692	13.689	31.881
32x32 crop	34.827	15.781	5.388	39.109	23.776	67.620
32x32 crop center	24.936	11.443	11.921	0.000	12.075	52.352

Table 20. MAE between embedded and extracted watermark against cropping attack using row Haar and row Haar wavelet transform

Cropping type	Row Haar wavelet					Row Haar
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Haar
16x16 crop	5.037	4.499	5.230	4.049	4.270	4.305
32x32 crop	21.545	8.651	12.046	19.423	18.277	24.729
32x32 crop center	2.984	3.253	1.571	0.000	2.384	0.000

Table 21. MAE between embedded and extracted watermark against cropping attack using row Walsh and row Walsh wavelet transform

Cropping type	Row Walsh wavelet					Row Walsh
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Walsh
16x16 crop	4.049	5.275	7.439	14.327	14.326	19.976
32x32 crop	13.518	31.544	15.550	35.988	35.987	37.892
32x32 crop center	4.973	2.549	26.627	21.477	21.477	31.042

Table 22. MAE between embedded and extracted watermark against cropping attack using row Kekre transform and row Kekre wavelet transform

Cropping type	Row Kekre wavelet					Row Kekre Transform
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Kekre Transform
16x16 crop	14.207	1.892	20.647	4.835	50.308	40.301
32x32 crop	18.353	6.368	5.531	10.123	202.193	112.438
32x32 crop center	14.940	14.125	129.946	0.000	31.970	129.552

Table 23. MAE between embedded and extracted watermark against cropping attack using row RFT and row RFT wavelet transform

Cropping type	Row RFT wavelet					Row RFT
Cropping type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row RFT
16x16 crop	4.050	2.774	13.907	7.404	45.755	42.124
32x32 crop	18.385	24.856	25.190	20.668	74.147	68.542
32x32 crop center	2.028	3.820	29.133	0.000	46.174	56.045

Table 24. MAE values between embedded and extracted watermark from different types of binary run length noises and Gaussian distributed noise added to watermarked images using column DCT and column DCT wavelet for embedding and extraction

Noise type	Column DCT wavelet					Column DCT
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column DCT
BRLN	0.000	0.000	0.000	0.000	0.000	0.000
BRLN (5to50)	8.277	7.108	8.366	7.662	10.306	13.784
BRLN (10 to 100)	8.191	7.564	9.443	7.512	9.914	13.208
GRLN	0.728	0.534	0.908	0.560	0.941	1.286

Table 16 to Table 19 show the performance of other column wavelets and corresponding orthogonal column

transforms against cropping attack. For different types of cropping performed on watermarked images, different

C. Noise addition to watermarked images

Two types of noises are added to watermarked images namely binary distributed random noise having magnitude 1or -1. Binary distributed random noise is added to watermarked images with different run lengths like run length 1 to 10, 5 to 50 and 10 to 100 to study the impact of increased noise. Another type of noise added to

watermarked images is Gaussian distributed run length noise. It has discrete magnitude in the range [-2, 2]. Watermarked images and extracted watermark from binary distributed run length noise with run length 10 to 100 are shown in Fig. 5 using column DCT and column DCT wavelet used for embedding watermark.

№№

University

ЖЛМЗ

University

MMIMSi

University

MMIMSI University

7.512

4.923

0.517

13.208

DCT column transform

DCT wavelet column transform (64,4)

DCT row transform

DCT wavelet row transform (32,8)

Fig. 5. Result images for binary distributed run length noise with run length 10 to 100 attack when DCT column, DCT wavelet column, DCT row and DCT wavelet row transform is used to embed watermark

From Fig. 5, it can be seen that use of column and row DCT wavelet transform significantly improves the robustness over use of column and row DCT used for embedding watermark. Table 24 shows MAE between

embedded and extracted watermark after adding different type of noises to watermarked image for column DCT and column DCT wavelet transform.

From Table 24 it can be observed that wavelet transform works equally well for smaller run length and significantly better than orthogonal transform for increased run length noise. For Gaussian distributed run length noise also all combinations tried for wavelet transform using DCT give better robustness.

Table 25 shows performance of row DCT and row DCT wavelet transform against noise addition attack in the form of MAE between embedded and extracted watermark. From Table 25 it can be seen that wavelet transform in row version also performs better than row DCT transform.

Table 25. MAE values between embedded and extracted watermark from noise added watermarked images when Row DCT and Row DCT wavelet transform is used for embedding and extracting watermark

Noise type	Row DCT wavelet					Row DCT
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row DCT
BRLN	3.916	4.378	4.614	4.245	4.575	6.573
BRLN (5to50)	1.963	1.695	2.122	1.667	2.525	2.539
BRLN (10 to 100)	1.195	1.059	1.344	1.071	1.797	2.071
GRLN	7.163	6.036	8.123	5.089	8.930	11.431

Table 26. MAE values between embedded and extracted watermark from different types of noises added to watermarked images using column Haar and column Haar wavelet for embedding and extraction

Noise type	Column Haar wavelet					Column Haar
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Haar
BRLN	0.000	0.000	0.000	0.000	0.000	0.000
BRLN (5to50)	5.366	5.378	5.191	8.340	5.763	6.947
BRLN (10 to 100)	5.045	5.634	5.768	7.279	5.673	7.496
GRLN	0.493	0.370	0.260	0.217	0.388	0.201

Table 27. MAE values between embedded and extracted watermark from different types of noises added to watermarked images using column Walsh and column Walsh wavelet for embedding and extraction

Noise type	Column Walsh wavelet					Column Walsh
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Walsh
BRLN	0.000	0.000	0.000	0.000	0.000	0.000
BRLN (5to50)	6.481	6.714	7.757	6.984	6.984	11.445
BRLN (10 to 100)	6.537	7.017	7.231	6.928	6.928	10.942
GRLN	0.915	0.558	1.116	0.863	0.863	2.176

Table 28. MAE values between embedded and extracted watermark from different types of noises added to watermarked images using column Kekre Transform and column Kekre wavelet for embedding and extraction

Noise type	Column Kekre wavelet					Column Kekre Transform
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Kekre Transform
BRLN	0.000	0.000	0.000	0.000	0.000	0.000
BRLN (5to50)	5.163	5.520	4.948	7.749	5.117	5.475
BRLN (10 to 100)	5.369	5.628	4.815	8.304	5.235	5.476
GRLN	0.720	0.287	1.353	0.082	1.914	3.787

Table 29. MAE values between embedded and extracted watermark from different types of noises added to watermarked images using column RFT and column RFT wavelet for embedding and extraction

Noise type	Column RFT wavelet					Column RFT
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column RFT
BRLN	0.000	0.000	0.000	0.000	0.000	0.000
BRLN (5to50)	8.128	7.324	9.278	6.939	7.917	14.901
BRLN (10 to 100)	7.789	6.632	9.200	7.831	7.863	12.788
GRLN	0.547	0.753	1.087	0.371	0.689	1.453

Similar response is observed by row wavelet show this response in the form MAE values. transforms over row transforms. Table 30 to Table 33

Table 30. MAE values between embedded and extracted watermark from noise added watermarked images when Row Haar and Row Haar wavelet transform is used for embedding and extracting watermark

Noise type	Row Haar wavelet					Row Haar
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Haar
BRLN	4.399	3.925	3.427	3.881	3.465	4.642
BRLN (5to50)	1.145	1.088	1.526	1.825	2.018	1.843
BRLN (10 to 100)	0.981	0.735	1.078	1.273	0.594	1.357
GRLN	4.879	5.797	5.189	5.139	5.103	5.262

Table 31. MAE values between embedded and extracted watermark from noise added watermarked images when Row Walsh and Row Walsh wavelet transform is used for embedding and extracting watermark

Noise type	Row Walsh wavelet					Row Walsh
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Walsh
BRLN	4.568	4.435	5.313	6.373	6.373	6.822
BRLN (5to50)	2.036	1.825	2.554	2.799	2.799	3.549
BRLN (10 to 100)	1.675	1.370	1.987	2.254	2.254	2.697
GRLN	6.913	6.268	7.289	7.672	7.672	8.887

Table 32. MAE values between embedded and extracted watermark from noise added watermarked images when Row Kekre transform and Row Kekre wavelet transform is used for embedding and extracting watermark

Noise type	Row Kekre wavelet					Row Kekre Transform
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Kekre Transform
BRLN	4.744	5.342	5.301	5.075	5.379	6.244
BRLN (5to50)	2.107	1.971	3.129	1.810	4.870	5.975
BRLN (10 to 100)	1.886	0.834	2.255	1.186	3.516	5.802
GRLN	5.206	5.912	5.494	7.036	5.576	5.601

Table 33. MAE values between embedded and extracted watermark from noise added watermarked images when Row RFT and Row RFT wavelet transform is used for embedding and extracting watermark

Noise type	Row RFT wavelet					Row RFT
Noise type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row RFT
BRLN	4.385	4.032	5.119	3.395	5.293	5.966
BRLN (5to50)	1.857	1.814	2.631	1.466	2.422	2.686
BRLN (10 to 100)	1.701	1.024	1.762	0.337	1.903	2.057
GRLN	7.036	6.111	7.426	5.041	9.018	10.453

Table 26 to Table 29 show MAE values between embedded and recovered watermark when column Haar and its wavelet, column Walsh and its wavelet, column Kekre transform and its wavelet and column RFT and its wavelet are used to embed and extract watermark and different types of noise addition is done to watermarked images. From these tables, it is concluded that wavelet

transforms obtained from orthogonal transforms are more robust to noise addition attacks than corresponding orthogonal transforms. Different combinations of orthogonal transforms used in generation of wavelet give different MAE values. But most of them are smaller than orthogonal column transforms or negligibly higher.

D. Resizing attack on watermarked images

Resizing attack is performed using three different techniques. First using bicubic interpolation in which watermarked image is doubled in size and then reduced back to its original size. Also watermarked image is zoomed to make it four times larger and then reduced back to its original size. Second approach used for resizing attack is using grid based image zooming technique proposed in [12]. In this approach image is doubled and reduced back to its original size. Third

approach is using transform based image zooming technique [14]. In this third approach, watermarked image is doubled in size using different orthogonal transforms like DCT, DST, DFT, Hartley and Real Fourier Transform.

Fig. 6 shows the result images for grid based resizing attack when column and row versions of DCT and DCT wavelet are used for embedding and extracting watermark.

0.028

32.627

2.968

0.027

35.062

2.247

DCT column transform

DCT row transform

DCT wavelet row transform (64,4)

DCT wavelet column transform (64,4)

Fig. 6. Extracted watermark from grid based resized watermarked images when DCT column, DCT wavelet column, DCT row and DCT wavelet row transform is used to embed watermark

From Fig. 6, the difference between performances against grid based resizing attack when column/row DCT and column/row DCT wavelet is used for embedding watermark is clearly seen. DCT Wavelet transforms in column and row version provides more robustness than DCT column and row transform.

Table 34 and Table 35 show the MAE values between embedded and extracted watermark against various resizing attacks using column version and row version of DCT/ DCT wavelet transform respectively.

Table 34. MAE values against resizing attacks when column DCT and column DCT wavelet are used to embed and extract watermark

Resizing type	Column DCT wavelet					Column DCT
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column DCT
Resize4	26.287	28.717	27.400	31.221	28.090	29.670
Resize2	27.028	29.494	28.178	32.038	28.875	30.502
DFT_resize2	1.566	1.798	1.536	1.755	1.793	2.023
grid resize2	4.398	3.365	5.305	2.968	8.566	32.627

Table 35. MAE values against resizing attacks when row DCT and row DCT wavelet are used to embed and extract watermark

Resizing type Row DCT wavelet Row DCT (16,16) (32,8) (8,32) (64,4) (4,64) Resize4 26.209 31.090 25.947 32.595 27.360 28.501 Resize2 26.899 31.924 26.661 33.464 28.127 29.294 DFT_resize2 1.903 1.693 1.791 1.445 2.252 2.515 grid resize2 4.253 3.358 5.527 2.247 9.375 35.062 transform and Real Fourier transform and corresponding resizing attack.

column transforms respectively against different types of

Table 36. MAE values against resizing attacks when column Haar and column Haar wavelet are used to embed and extract watermark

Resizing type	Column Haar wavelet					Column Haar
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Haar
Resize4	27.180	27.962	29.182	27.791	27.267	27.688
Resize2	27.912	28.705	29.962	28.532	27.994	28.422
DFT_resize2	1.086	1.129	1.128	1.230	1.091	1.199
grid resize2	3.029	3.048	3.087	4.319	3.179	4.339

Table 37. MAE values against resizing attacks when column Walsh and column Walsh wavelet are used to embed and extract watermark

Resizing type	Column Walsh wavelet					Column Walsh
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Walsh
Resize4	28.859	28.273	29.121	28.751	28.751	30.001
Resize2	29.675	29.049	29.934	29.552	29.552	30.836
DFT_resize2	1.206	1.203	1.043	1.151	1.151	1.625
grid resize2	8.105	6.222	11.381	8.570	8.570	55.839

Table 38. MAE values against resizing attacks when column Kekre Transform and column Kekre wavelet Transform are used to embed and extract watermark

Resizing type	Column Kekre wavelet					Column Kekre Transform
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column Kekre Transform
Resize4	35.914	38.134	36.762	38.913	38.020	38.538
Resize2	36.810	39.058	37.689	39.880	38.973	39.510
DFT_resize2	1.708	1.905	1.547	2.327	1.622	1.688
grid resize2	2.045	2.066	1.901	3.061	2.119	1.867

Table 39. MAE values against resizing attacks when column DFT and column DFT wavelet are used to embed and extract watermark

Resizing type	Column RFT wavelet					Column RFT
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Column RFT
Resize4	27.746	29.338	28.752	31.383	29.305	30.610
Resize2	28.549	30.148	29.575	32.207	30.120	31.473
DFT_resize2	1.435	1.405	1.427	1.386	1.413	2.126
grid resize2	3.703	3.412	4.480	3.003	3.650	31.587

Performance against resizing attack using orthogonal transforms in terms of MAE between embedded and row transforms Haar, Walsh, Kekre Transform and Real extracted watermark is given in Table 40 to Table 43.

Fourier Transform and corresponding row wavelet

Table 40. MAE values against resizing attacks when row Haar and row Haar wavelet are used to embed and extract watermark

Resizing type	Row Haar wavelet					Row Haar
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Haar
Resize4	29.846	30.331	29.255	28.777	29.455	29.205
Resize2	30.665	31.156	30.058	29.573	30.257	30.013
DFT_resize2	1.177	1.338	1.077	1.094	1.188	1.225
grid resize2	3.583	4.028	3.919	3.864	3.396	4.106

From Table 40, it can be observed that Row Haar Haar transform for each type of resizing attack. wavelet transform performs marginally better than Row

From Table 41, it can be concluded that for bicubic interpolation, Row Walsh is marginally better than Row Walsh wavelet transform. For DFT based resizing, Row Walsh wavelet obtained from (16,16), (32,8) and (8,32) combinations give marginally better MAE values and (64,4) and (4,64) combinations give almost equal MAE

values and hence overall performance of Row Walsh wavelet can be considered acceptable over Row Walsh transform. For grid based resizing, significant improvement is observed by Row Walsh wavelet over Row Walsh transform. Similar observations are noted for row versions of Kekre Transform and Kekre wavelet

Table 41. MAE values against resizing attacks when row Walsh and row Walsh wavelet are used to embed and extract watermark

Resizing type	Row Walsh wavelet					Row Walsh
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Walsh
Resize4	31.345	32.915	31.941	33.634	33.633	30.878
Resize2	32.212	33.828	32.830	34.565	34.565	31.736
DFT_resize2	1.314	1.355	1.468	1.624	1.624	1.605
grid resize2	8.197	5.476	13.385	19.463	19.46299	42.759

Transform and also for row version of RFT and RFT wavelet transform.

VI. C omparison of wavelet transforms against ATTACKS

In previous section, performance of orthogonal transform with their wavelet transform has been done. All those wavelet transforms are compared in this section.

For each attack, the best size combination of each wavelet transform is selected for comparison.

Fig. 7 below shows performance of Column DCT wavelet (CDW), Column Haar wavelet (CHW), Column Walsh wavelet (CWW), Column Kekre wavelet (CKW) and Column Real Fourier Wavelet (CRW) transforms against compression using DCT, Walsh, Haar and DST.

DCT ■ DST ■ Walsh ■ Haar

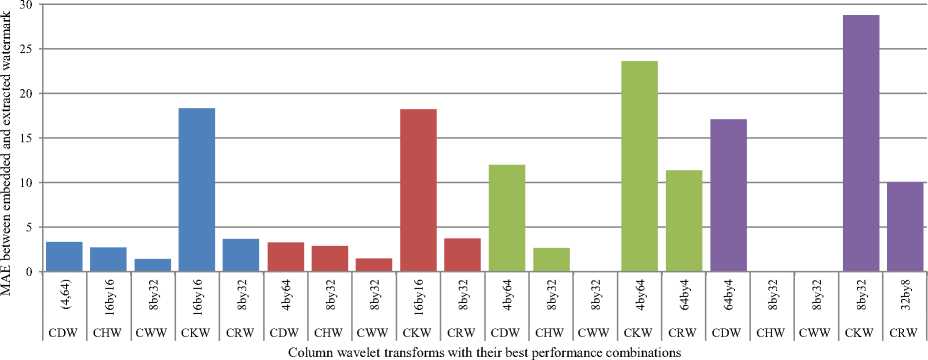
Fig. 7 Comparison of MAE between embedded and extracted watermark against compression using DCT, DST, Walsh and Haar when column DCT wavelet, Column Haar wavelet(CHW), Column Walsh wavelet(CWW), Column Kekre wavelet (CKW) and Column Real Fourier Wavelet (CRW) transforms are used for embedding watermark

From Fig. 7, column Walsh wavelet obtained from Walsh transform of size 8x8 and 32x32 is observed to be the best performer against compression using DCT, DST, Walsh and Haar. Column Haar wavelet transform closely follows it.

Fig. 8 shows the performance comparison of row DCT wavelet (RDW), row Haar wavelet (RHW), row Walsh wavelet (RWW), Row Kekre wavelet (RKW) and row Real Fourier wavelet transform (RRW) transforms against DCT, DST, Walsh and Haar based compression.

Table 42. MAE values against resizing attacks when row Kekre Transform and row Kekre wavelet Transform are used to embed and extract watermark

Resizing type	Row Kekre wavelet					Row Kekre Transform
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row Kekre Transform
Resize4	38.665	36.889	37.671	38.595	38.817	39.943
Resize2	39.627	37.810	38.608	39.547	39.781	40.953
FFT_resize2	1.795	1.828	1.581	2.119	1.735	1.605
grid resize2	2.097	2.479	1.997	2.764	2.479	2.183

Table 43. MAE values against resizing attacks when row RFT and row RFT wavelet are used to embed and extract watermark

Resizing type	Row RFT wavelet					Row RFT
Resizing type	(16,16)	(32,8)	(8,32)	(64,4)	(4,64)	Row RFT
Resize4	29.667	31.734	28.968	30.947	27.833	26.654
Resize2	30.486	32.606	29.779	31.794	28.629	27.397
FFT_resize2	1.604	1.430	1.660	1.226	2.032	2.382
grid resize2	3.890	3.563	5.430	2.170	9.638	30.373

From Table 34 and Table 35, it is observed that column and row DCT wavelet transforms perform marginally better against resizing using bicubic interpolation attack and resizing using DFT. Against resizing using grid based interpolation, performance of column and row DCT wavelet is far better than column and row DCT respectively. Another noticeable

observation regarding transform based resizing attack is that MAE between embed and extracted watermark is observed to be zero using DCT, DST, Hartley and Real Fourier Transform irrespective of the transform used for embedding and extraction process.

Table 36 to Table 39 show the performance of column wavelet transforms obtained from Haar, Walsh, Kekre

■ DCT -DST ■ Walsh "MHaar

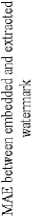
Row wavelet transforms with their best performance combinations

Fig. 8. Comparison of MAE between embedded and extracted watermark against compression using DCT, DST, Walsh and Haar when row DCT wavelet (RDW), row Haar wavelet(RHW), row Walsh wavelet(RWW), row Kekre wavelet (RKW) and row Real Fourier Wavelet (RRW) transforms are used for embedding watermark

Row Walsh wavelet closely followed by row Haar wavelet transform are most robust against compression using DCT, DST, Walsh and Haar as can be observed from Fig. 8.

Fig. 9 and Fig. 10 show comparison of column transforms and row transforms respectively against compression using DCT wavelet, JPEG compression and VQ based compression.

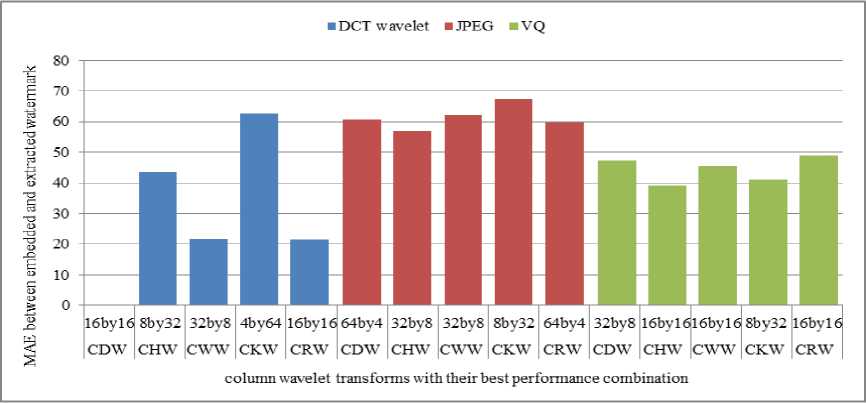
Fig. 9. Comparison of MAE between embedded and extracted watermark against compression using DCT wavelet, JPEG and VQ when column DCT wavelet, Column Haar wavelet(CHW), Column Walsh wavelet(CWW), Column Kekre wavelet (CKW) and Column Real Fourier Wavelet (CRW) transforms are used for embedding watermark

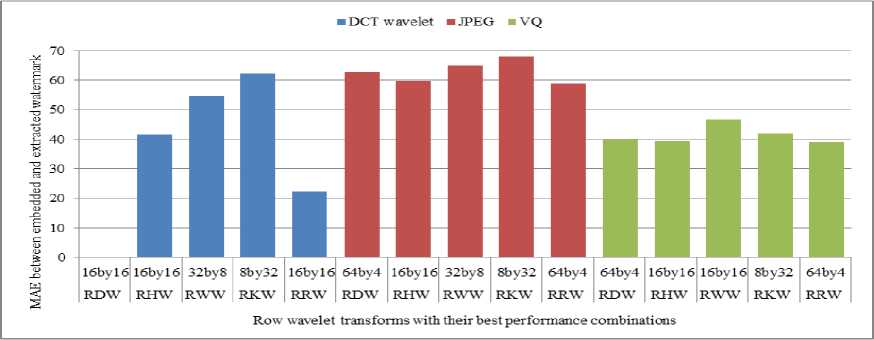
Fig. 10. Comparison of MAE between embedded and extracted watermark against compression using DCT wavelet, JPEG and VQ when row DCT wavelet (RDW), row Haar wavelet(RHW), row Walsh wavelet(RWW), row Kekre wavelet (RKW) and row Real Fourier Wavelet (RRW) transforms are used for embedding watermark

From Fig. 9 and 10 it can be seen that for compression using column DCT wavelet, column DCT wavelet and row DCT wavelet obtained from 16x16 size DCT matrix give best robustness with MAE zero. For JPEG compression column Haar wavelet (32, 8) and row Real Fourier wavelet (64, 4) are better than other column and row wavelet transforms. For VQ based compression, column and row Haar wavelet obtained from (16, 16) size Haar matrix are better.

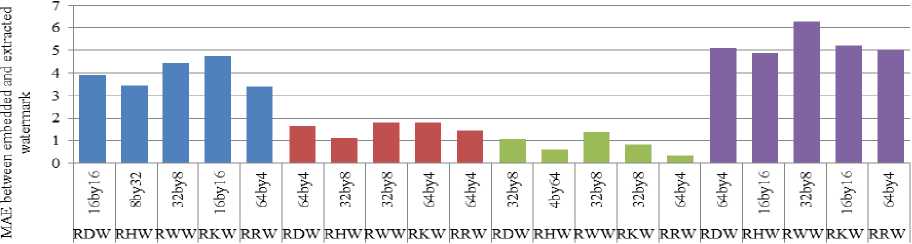
Comparison of column wavelet transforms and row wavelet transforms against cropping attack is shown in Fig. 11 and Fig. 12 respectively.

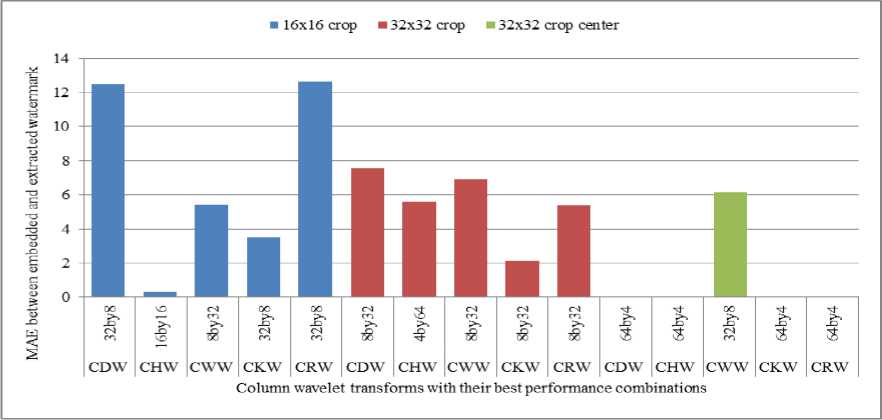
Fig. 11. Comparison of MAE between embedded and extracted watermark against cropping when column DCT wavelet, Column Haar wavelet(CHW), Column Walsh wavelet(CWW), Column Kekre wavelet (CKW) and Column Real Fourier Wavelet (CRW) transforms are used for embedding watermark

From Fig. 11, it is observed that as we increase amount of cropped portion at corners, MAE between embedded and extracted watermark is reduced except for column Haar transform. For 16x16 cropping, column Haar wavelet transform and for 32x32 cropping at corners, column Kekre wavelet transform are observed to be robust than others. For 32x32 cropping at center, except

Walsh column wavelet all other column wavelet transforms show outstanding robustness with MAE zero. This is applicable for row wavelet transforms shown in Fig. 12. Row DCT wavelet and row Kekre wavelet are more robust against 16x16 and 32x32 cropping at corners respectively.

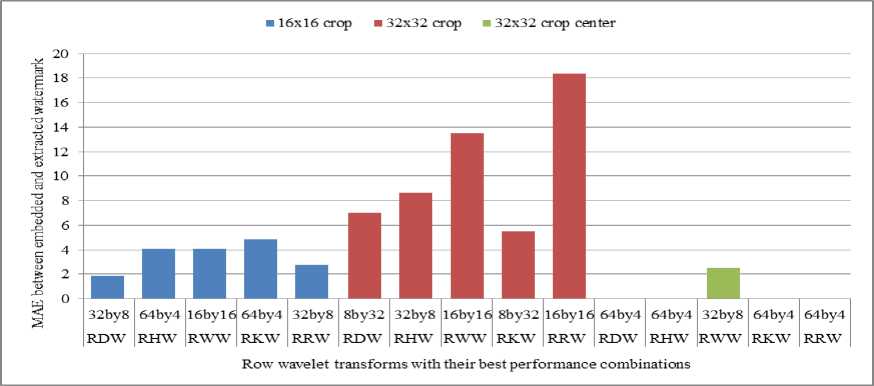
Fig. 12. Comparison of MAE between embedded and extracted watermark against cropping when row DCT wavelet (RDW), row Haar wavelet(RHW), row Walsh wavelet(RWW), row Kekre wavelet (RKW) and row Real Fourier Wavelet (RRW) transforms are used for embedding watermark

Fig. 13 and Fig. 14 show performance comparison of column wavelets and row wavelets respectively against noise addition attack. All column transforms show zero MAE against Binary distributed run length noise with run length 1 to 10 and hence not shown in Fig. 13. For higher run length of binary distributed run length noise and for Gaussian distributed run length noise, column Kekre wavelet is observed to be most robust.

■ BRLN (5to50) ■ BRLN (10 to 100) ■ GRLN

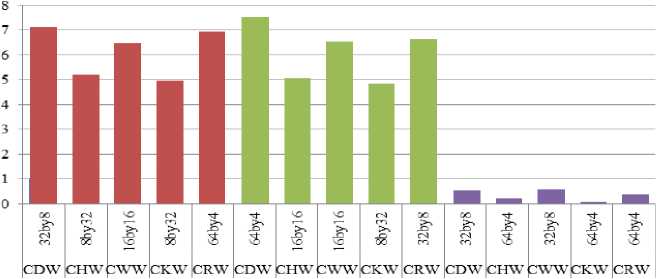
Column wavelet transforms with their best performance combinations

Fig. 13. Comparison of MAE between embedded and extracted watermark against noise addition when column DCT wavelet, Column Haar wavelet(CHW), Column Walsh wavelet(CWW), Column Kekre wavelet (CKW) and Column Real Fourier Wavelet (CRW) transforms are used for embedding watermark

■ BRLN *BRLN (5to50) bBRLN (10 to 100) ■ GRLN

Row wavelet transforms with their best performance combinations

Fig. 14. Comparison of MAE between embedded and extracted watermark against noise addition when row DCT wavelet (RDW), row Haar wavelet(RHW), row Walsh wavelet(RWW), row Kekre wavelet (RKW) and row Real Fourier Wavelet (RRW) transforms are used for embedding watermark

From Fig. 14, it is observed that for all varieties of noise addition attack, except binary distributed run length noise with 10 to 100 run length Haar wavelet is better in robustness. Real Fourier row wavelet transform is slightly better than Row Haar wavelet for 10 to 100 run length of binary distributed run length noise

Fig. 15 shows comparison of column wavelet transforms and Fig. 16 shows comparison of row wavelet transforms against various resizing attacks.

■ Resize4 ■ Resize2 ■ DFT_Resize2 ■ grid resize2

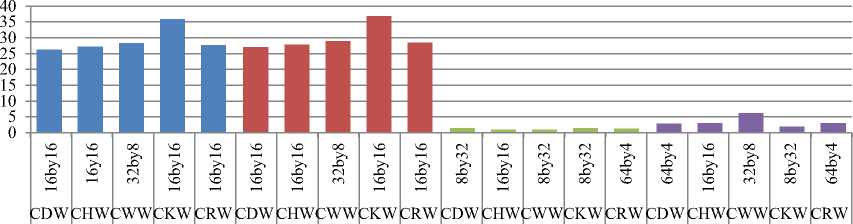
Column wavelet transforms with their best performace combinations

Fig. 15. Comparison of MAE between embedded and extracted watermark against resizing attack when column DCT wavelet, Column Haar wavelet(CHW), Column Walsh wavelet(CWW), Column Kekre wavelet (CKW) and Column Real Fourier Wavelet (CRW) transforms are used for embedding watermark

■ Resize4 eResize2 eDFT_Resize2 ■gridresize2

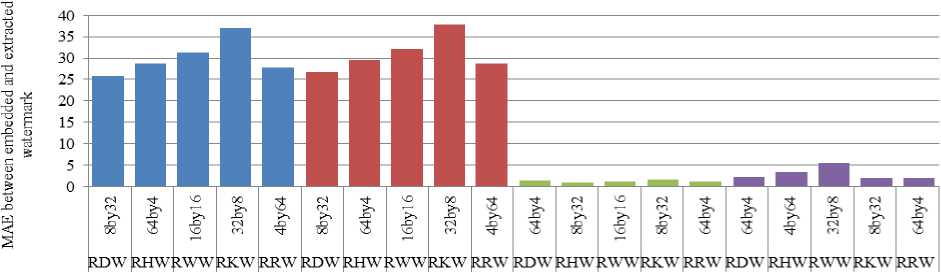
Row wavelet transforms with their best performance combinations

Fig. 16. Comparison of MAE between embedded and extracted watermark against resizing attack when row DCT wavelet (RDW), row Haar wavelet(RHW), row Walsh wavelet(RWW), row Kekre wavelet (RKW) and row Real Fourier Wavelet (RRW) transforms are used for embedding watermark

From Fig. 15 and 16 we can observe that column and row DCT wavelet show better robustness than other column and row transforms against resizing using bicubic interpolation which is named as Resize4 and Resize2 in graphs. For DFT based resizing all column wavelet transforms as well as row wavelet transforms show negligible difference in performance. For grid based resizing, column and row Kekre wavelet transforms are better than other column and row wavelet transforms respectively.

VII. C onclusion

The proposed method uses orthogonal transforms DCT, Haar, Walsh, Kekre transform and Real Fourier Transform and their wavelets generated using different size combinations of these orthogonal transforms. Wavelet transforms when used with SVD for embedding watermark give better robustness than orthogonal transforms with SVD. For different attacks, different size combination of orthogonal transform used to generate wavelet transform gives best robustness and the overall performance of wavelet transforms is better than orthogonal transform in column and row version. Wavelet transforms when compared, different wavelets are found to be good in robustness against different attacks.

Список литературы Performance Comparison of Watermarking Using SVD with Orthogonal Transforms and Their Wavelet Transforms

Veysel Aslantas, A. Latif Dogan and Serkan Ozturk, "DWT-SVD based image watermarking using particle swarm optimizer", Proc. of IEEE International Conference on Multimedia and Expo, pp. 241-244. 2008.
Yang Quianli, Cai Yanhong, "A digital watermarking algorithm based on DWT and DCT", IEEE International Symposium on Information Technology in Medicine and Education, pp. 1102-1105, 2012.
Xi-Ping he and Qing-Sheng Zhu, "A robust wavelet-domain watermarking algorithm for colour image", Proceedings of the fifth international conference on machine learning and cybernetics, Dalian, pp.13-16, August 2006.
Zhen Li, Kim-Hui Yap and Bai-Ying Lei, "A new blind robust image watermarking scheme in SVD-DCT composite domain", In Proc. of 18th IEEE international conference on Image Processing, pp. 2757-2760, 2011.
Rahim Ansari, Mrutyunjaya M Devanalamath, K. Manikantan, S. Ramachandran, "Robust digital image watermarking algorithm in DWT-DFT-SVD domain for colour images", Proc. of IEEE International Conference on Communication, Information & Computing Technology (ICCICT), Oct. 19-20 2012, Mumbai, India, pp. 1-6, Oct 2012.
Zhen Li, Kim-Hui Yap and Bai-Ying Lei, "A new blind robust image watermarking scheme in SVD-DCT composite Domain", 18th IEEE International Conference on Image Processing, 2011, pp. 2757-2760, 1987.
Yan Dejun, Yang Rijing, Li Hongyan, and Zheng Jiangchao, "A Digital Watermarking Scheme Based On Singular Value Decomposition and Discrete Wavelet Transform", In IEEE Proc. of International Conference on Computer Science and Network Technology, pp. 154-157, 2011.
Krzysztof Simek, "Properties of SVD based dynamical model of gene expressing data", International Journal of Applied Maths Computer Science, Vol. 13, No. 3, pp. 337-345, 2003.G.Wyszecki and W.Stiles, Color Science: Concepts and Metheds, Quantitative Data and Formulae, 2nd ed. New York: Wiley, 1982.
Cao, Lijie, "Singular value decomposition applied to digital image processing", Division of Computing Studies, Arizona State University Polytechnic Campus, Mesa, 2006.
Ruizhen Liu, Tieniu Tan, "A SVD based watermarking scheme for protecting rightful ownership", IEEE transactions on multimedia, vol. 4, pp. 121-128, March 2002.
Kekre, H. B., Archana Athawale, Dipali Sadavarti, "Algorithm to Generate Wavelet Transform from an Orthogonal Transform." International Journal of Image Processing (IJIP) 4.4 (2010): 444
H. B. Kekre, Tanuja Sarode, Sudeep Thepade. "Grid based image scaling technique", International Journal of Computer Science and Applications, Volume 1, No. 2, pp. 95-98, August 2008.
I. J. Cox, J. Killian, F. T. Leighton, T. Shamoon, "Secure spread spectrum watermarking for multimedia", IEEE Transaction on Image Processing, 6(12), pp. 1673-1687, 1997.
Dr. H. B. Kekre, Dr. Tanuja Sarode, Shachi Natu. "Image zooming using Sinusoidal Transforms like Hartley, DFT, DCT, DST and Real Fourier Transform", selected for publication in International journal of computer science and information security Vol. 12 No. 7, July 2014.
H. B. Kekre, Tanuja Sarode, Sudeep Thepade, "Inception of Hybrid Wavelet Transform using Two Orthogonal Transforms and It's use for Image Compression", International Journal of Computer Science and Information Security, volume 9, No. 6, pp. 80-87, 2011.

Еще

Статья научная