Performance Evaluation of Unslotted CSMA/CA for Wireless Sensor Networks: Energy Consumption Analysis and Cross Layer Routing

Published Online June 2017 in MECS DOI: 10.5815/ijcnis.2017.06.01

Wireless sensor networks (WSNs) become very notorious and are used in a large panel of applications (smart cities, smart grids, e-health, etc.). Several factors contribute to the notoriety of WSNs. For instance, these networks are composed of hundreds, thousands of small devices called sensors that communicate together to achieve a particular task in the network. Each sensor has an individual energy resource (battery), a sensing and a communication modules to ensure capturing events and sending them to the sink node. Moreover, sensor nodes have non negligible processing capabilities which allow them performing very advanced tasks such as data aggregation, data fusion, clustering, etc.

Despite their robustness:  self-organization, fault tolerance, autonomy, WSNs present some weaknesses regarding their critical energy resource. For instance, in WSNs, sensor nodes are equipped with finite batteries. If the energy resource depletes within a sensor node, this node is considered as a failed node and could no more participate in the sensing/communication activities in the network. Moreover, it is quasi impossible to change the energy resource within a sensor due to the harsh environment in which these nodes are generally deployed. In addition, thank to miniaturization in the MEMS (Micro-Electro-Mechanical Systems), equipping a sensor node with a new battery may be more expensive than the node itself. Therefore, when a sensor node energy depletes, we generally prefer exploiting the spacial redundancy in the network to ensure that the sensing tasks previously performed by the failed sensor could be replaced by its one hop neighbors. Nevertheless, the sensor nodes' spacial redundancy cannot be used as a sustainable solution to the energy depletion problem in WSNs (especially in sparse networks where repetitive nodes' failures may cause coverage/connectivity holes hence disturbing the correct network functioning). Thus, several mechanisms need to be implemented early in WSNs to prevent the energy depletion problem and maximizing the whole network lifetime.

Optimizing the energy consumption in WSNs, was largely considered in literature [22], [31], [21], [15], [19] at different abstraction levels (medium access, synchronization, multi-channel, routing, etc.). At the MAC layer, for instance, the IEEE 802.15.4 standard [13] proposes two medium access techniques for low rate wireless PANs (Personal Area Networks). This standard suits WSNs since the proposed medium access schemes considers the sensor nodes characteristics (low power, limited memory/energy, etc.). The IEEE 802.15.4 standard was adopted by several WSNs technologies such as Zigbee [33] and 6Lowpan [15], an adaptation of the IPv6 network layer to low power and lossy networks (LLNs). It introduces the beacon enabled scheme based on the slotted CSMA/CA (Carrier Sense Multiple Access with Collision Avoidance) algorithm. This scheme is used in the presence of a PAN coordinator and requires the synchronization between the sensor nodes.

In the absence of a coordinator, in a multihop environment for instance, the slotted IEEE 802.15.4 becomes inappropriate. The beaconless IEEE 802.15.4 scheme can therefore be used. Several approaches were proposed in literature to evaluate the performance of both slotted and unslotted CSMA/CA schemes in terms of average energy consumption, delay, throughput, etc. However, few works consider accurate energy consumption bounds of the unslotted CSMA/CA. In this paper, we focus on the unslotted CSMA/CA protocol as the medium access scheme in WSNs adapted to multihop communications in the absence of PAN coordinators. Several works in literature evaluated the performance of the beaconless IEEE 802.15.4 in terms of delay, achieved throughput and average energy consumption. But, none of the proposed studies derived energy consumption bounds of the proposed scheme. Hence, our contribution in this paper is twofold. First, we propose a comprehensive energy consumption study of the unslotted CSMA/CA under unsaturated traffic conditions. Our study is based on the analysis of the discrete time Markov chain ( DTMC ) modelling the beaconless IEEE 802.15.4 backoff process [5]. Then, we derive probabilistic energy consumption bounds and the approximated average energy consumption of the unslotted CSMA/CA. Energy consumption bounds are expressed as the probability that the energy consumption within a sensor node exceeds a certain value. We also derive the approximated average energy consumption of the unslotted CSMA/CA. For instance, the approximated analysis provides simpler expressions of the energy consumption within a sensor that can be easily computed based on local estimated values. As a second contribution of this paper, we propose a cross layer routing scheme that exploits the approximated average energy computation we derived at the IEEE 802.15.4 MAC layer to enhance the behavior of the native Power-Efficient Gathering in Sensor Information Systems (PEGASIS) routing [19]. The choice of the PEGASIS routing is motivated by the fact that this scheme already outperforms several WSN dedicated routing protocols such as Low Energy Adaptive Clustering Hierarchy (LEACH) for example [10]. Our proposed scheme called Average Energy Enhanced PEGASIS (AE2-PEGASIS), intends to provide even better results than the native PEGASIS by considering not only the distance but also the dissipated energy when constructing the chain to the sink.

The rest of the paper is organized as follows. Section II presents the works related to our study and depicts the most significant solutions in literature interested in WSNs energy resource optimization at the MAC layer. In Section II, we also focus on the IEEE 802.15.4 standard, present the basics of the unslotted CSMA/CA medium access scheme and the different studies that evaluated its performance. In Section III, we propose a Markov chain based energy consumption analysis of the beaconless IEEE 802.15.4 standard. Hence, we derive the unslotted CSMA/CA energy consumption bounds and approximated average energy consumption. The analytical results are validated through simulations using the Omnet++ network simulator [30]. In Section IV, we propose the AE2-PEGASIS scheme that exploits the energy consumption analysis done in Section III to enhance the behavior of the native PEGASIS routing scheme. Finally, we conclude the paper in Section V.

• II.    Background and Related Work

In this Section, we present the major work related to our study. We first, present the most famous energy aware medium access techniques that suit the WSNs characteristics. Then, we describe in details the unslotted CSMA/CA algorithm proposed by the IEEE 802.15.4 standard for beaconless communications. Finally, we discuss the different solutions in literature that evaluated the performance of the unslotted CSMA/CA scheme.

• A.    Energy Aware MAC Techniques in WSNs

Several works in literature were interested in WSN energy resource optimization at the MAC layer. For instance, S-MAC [31] was proposed as an alternative to the IEEE 802.11 standard [12] for WSNs. S-MAC is based on the RTS/CTS (Request to Send/Clear to Send) mechanism and implements a distributed sleep/awake scheme where sensor nodes periodically awake, look if there are other nodes that would like to talk to them and return again to the sleep state. To synchronize the sleep/awake periods between sensor nodes, S-MAC defines a two phase super frame with active and inactive periods. At the beginning of the active period, the sensor nodes synchronize their transmissions by exchanging SYNC frames containing the sender's address and the remaining time till the next sleep period. Each node defines its scheduling based on the SYNC messages received by its neighbors. The main drawback of S-MAC is the overhead introduced by SYNC frames which may introduce several scheduling in the network.

As for S-MAC, the T-MAC protocol [4] uses the RTS/CTS mechanism and the sensor nodes periodically wake up to send their data. Each node can transmit while it is in an active state. Active periods end if the channel remains idle for a timeout period. The problem of T-MAC is that some nodes may go to the sleep state prematurely so they cannot be in a receiving state when data is available. Other approaches as D-MAC [22] and Wise MAC [7] enhanced the behavior of the native S-MAC protocol. D-MAC aims to deliver real time data but is not suited to high traffic loaded nodes. However, Wise MAC minimizes the energy consumption in S-MAC by eliminating the usage of both RTS/CTS and SYNC messages. But, it presents latency problems due to the lack of synchronization between the sensor nodes. Another protocol Berkley Media Access Control (B-MAC) [26] was proposed for WSNs using adaptive preamble scheme. But B-MAC was not designed to support message fragmentation and is unable to provide a low power policy. Protocols B-MAC+ [1] and X-MAC [3]

have been proposed to enhance the B-MAC behavior and improve its energy management scheme.

All the above mentioned works led to the emergence of the IEEE 802.15.4 standard [13] adapted to low rate wireless PANs and used by several implementations of WSNs such as Zigbee [33] and 6Lowpan [15], an adaption of the IPv6 stack to low power PANs. IEEE 802.15.4 defines slotted and unslotted MAC schemes depending on the presence or not of a coordinator point in the network.

• B.    Presentation of the Beaconless IEEE 802.15.4 Medium Access Scheme

The IEEE 802.15.4 standard [13] was proposed as the IEEE standard for low rate wireless PANs. It introduces the beacon enabled and the beaconless access modes. The beacon enabled mode is used in the presence of a PAN coordinator and is based on the slotted CSMA/CA. In a beaconless mode, the unslotted CSMA/CA scheme is used since the nodes contend for the channel without any coordination. This access scheme is privileged in a multihop environment.

The beaconless IEEE 802.15.4 medium access scheme is largely inspired from the native IEEE 802.11 Distributed Coordination Function (DCF) [12]. Hence, it is based on the unslotted CSMA/CA algorithm and introduces two variables: NB and BE . The variable ( BE ), representing the backoff exponent, is related to the number of backoff periods a device should wait before trying to access the channel. One backoff period is equal to aUnitBackoffPeriod (20 symbols, a symbol duration is equal to 16 µs ). The variable NB , representing the number of failed Clear Channel Assessments (CCA), is related to the current transmission attempt. A CCA is performed by the physical layer to detect an activity on the medium and report it to the MAC layer.

When a station has a packet to transmit, it initializes the variable NB to 0 and BE to macMinBE (the minimum backoff exponent) and picks a random backoff value in the time interval [0, 2 ^BE - 1]: When the backoff expires, the station performs a CCA to detect whether the channel is idle or not. If the channel is idle, a transmission attempt is started. If however the channel is busy, NB and BE values are increased by one while ensuring that BE ≤ macMaxBE (the maximum backoff exponent) and NB ≤ macMaxCSMABackoffs (the maximum number of channel access attempts for the current packet transmission). If NB is greater than macMaxCSMABackoffs , the backoff procedure terminates and the packet is discarded.

In the case of a successful packet transmission, an acknowledgement ( ACK ) is sent after an Inter Frame Space ( IFS ). If the sender fails to receive an ACK due to a collision or an acknowledgement timeout, the retransmission attempt number RT is increased by one up to macMaxFrameRetries . All the above described steps are therefore repeated until the packet is correctly received or discarded after macMaxFrameRetries transmission attempts.

• C.    Analysis of the Beaconless IEEE 802.15.4 Scheme

Both analytical and simulation studies focused on the performance evaluation of slotted an unslotted IEEE 802.15.4 medium access schemes. For instance, simulation studies in [20] and [17] evaluated the throughput, the delay and the energy consumption of both slotted and unslotted CSMA/CA. Analytical researches [24], [8], [5] were then proposed to analyze the IEEE 802.15.4 protocol behavior. The work done is these studies was mainly based on an early work done in [2] that evaluates the native IEEE 802.11 DCF under saturated traffic conditions using Markov chain analysis.

If we focus on the beaconless IEEE 802.15.4 MAC scheme, the authors in [8] proposed a Markov chain analysis that estimates the channel access probability of the unslotted CSMA/CA in multi-hop topologies. The results showed the accuracy of the predicted values using extensive simulations. In [5] and [6], the authors modified the Markov chain model of the beacon enabled IEEE 802.15.4 medium access scheme [24], [25] to adapt it to the unslotted case, in a multi-hop context under unsaturated, heterogeneous and hidden station conditions. The authors derived the average energy, the delay and the reliability within a link in the network and generalized the results to the multi-hop context. Results showed that routing over multi-hop networks is significantly influenced by the IEEE 802.15.4 MAC performance and that the traffic trends to be directed through nodes with high packet generation rates, which considerably increases the energy consumption.

In [18], the authors proposed a novel analytical model of the unslotted CSMA saturation throughput using a semi-Markov process that retrieves the interaction between MAC and PHY layers to derive the CCA output. Performance evaluation showed that the probability that CCA succeeds (respectively fails) clearly depends on the actual backoff stage. In [29], the authors developed an approximated analytical technique to evaluate multi-hop beaconless IEEE 802.15.4 networks. The analysis showed that the proposed scheme is accurate in the absence of hidden nodes and is relatively efficient in terms of packet discarded probability, failure probability and throughput with hidden nodes' scenarios. Recently, the authors in [11] proposed an adaptation of the unslotted CSMA/CA for mobile vehicles based on the M/G/1 queuing theory. Results depicted the impact of the vehicle speed on the protocol behavior. In [23], the authors evaluated the noise and the fading effects on the unslotted IEEE 802.15.4 MAC behavior and how do the results deviate from perfect channel conditions.

All the above mentioned studies only considered exact average energy consumption of unslotted CSMA/CA. None of the existing works derived either approximated energy consumption or energy consumption bounds of the beaconless IEEE 802.15.4 MAC. In the following, we derive approximated average and probabilistic energy consumption bounds of the beaconless IEEE 802.15.4 medium access scheme.

• III.    Energy Consumption Analysis of the Unslotted IEEE 802.15.4 MAC Scheme

• 802.15.4 medium access scheme. With an approximated computation, the average energy consumption can be easily derived using local estimations which can be exploited in the routing layer as detailed in Section IV.

In this section, we focus on the analysis of the beaconless IEEE 802.15.4 to derive energy consumption bounds at the medium access layer. Therefore, we briefly describe the Markov chain modeling the unslotted CSMA/CA as detailed in [5]. This Markov chain models the behavior of the unslotted CSMA/CA in a multi-hop context under hidden nodes and unsaturated traffic conditions. In our study, we restrict the analysis to the single hop context. We also derive the approximated average energy consumption of the beaconless IEEE

• A.    The Unslotted CSMA/CA Markov Chain

According to the description of the unslotted CSMA/CA given in Section II, the medium access backoff process can be modeled, within each node participating in the network, by a discrete time Markov chain (DTMC) [5], [24], [2], as described in the following Figure 1.

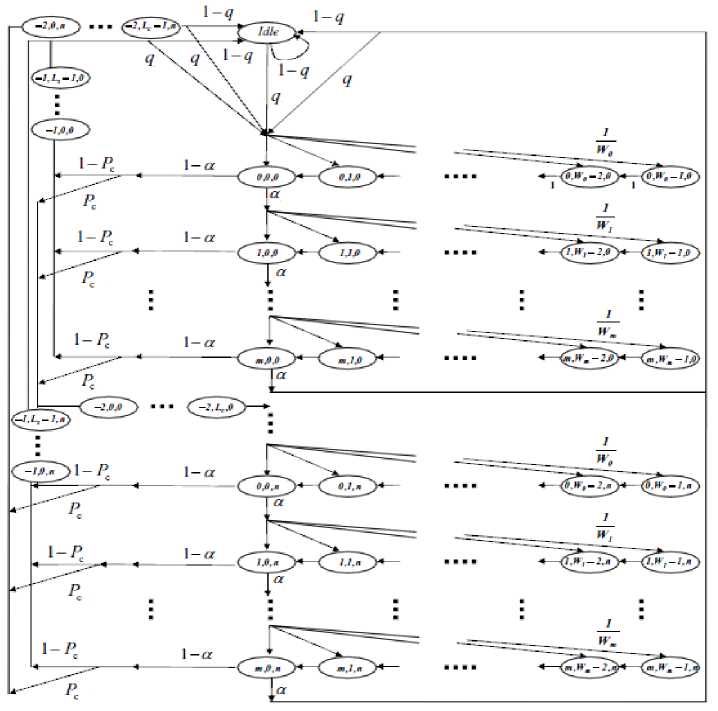
Fig.1. The Markov Chain Modelling the Unslotted CSMA/CA Backoff

Each state of the Markov chain is represented by the tuple (s(t), c(t), r(t)) , where s(t) is the stochastic process representing the backoff counter and the channel occupation by a correct transmission or a collision. c(t) (respectively r(t)) describes the backoff counter (respectively the retransmission attempt) at the time instant t. Let N, be the number of contending stations, α is the probability that the CCA is busy and q is the probability of packet generation in a time slot (the time slot duration is given by aUnitBackoffPeriod).We also define τ; the probability that a node attempts a first carrier sensing in a randomly chosen time slot. In the stationary conditions, τ is constant and independent of the other nodes. Moreover, we define m0 = macMinBE, mb = macMaxBE, W0 = 2*macMinBE, m = maxCSMABackoffs and n = macMaxFrameRetries.

From Figure 1, we define the Markov chain states: ( i , W i - k , j ) , ( i e [ 0, m ] , k e [ 0, W i - 1 ] , j e [ 0, n ] ) representing the case where a node is about to perform the i^th CCA at the j^th retransmission attempt and the current backoff value is W - k ) . In the idle state ( idle ), the node's queue is empty until a packet is generated with the probability q (in units of packets/slot ). The probability q is used to indicate that we are under unsaturated traffic conditions.

The states ( - 1, k , j ) , k e [ 0, L_s - 1 ] , j e [ 0, n ] and the states ( - 2, k , j ) , k e [ 0, L c - 1 ] and j e [ 0, n ] respectively model correct and colliding transmissions. L_s and L_c respectively determine the size of a correct and a colliding packet expressed as a number of slots as:

_ ccaDetectionTime + aTurnaroundTime s           aUnitBackoffPeriod

i e [ - 2, m ] , k e [ 0, max ( W i - 1, L_s - 1, L c - 1 ) ] , j e [ 0, n ] as a function of b . Then, using the normalization condition and for m <  m_b - m ₀, we have:

b 0,0,0

Г 1 f 1 - ( 2 a ) ^m 1 - a m ^{+ 1} ) 1 - y n ^{+ 1}

-I —— W0 +I —-—

_ 2 ^   1 - 2 a         1 - a J 1 - y

+ ( L s ( 1 - P c ) + L c P c ) ( 1 - a m ^{+ 1} )1-^ ^{n + 1 1 - y}

• 1    (   m+1 hn

+11 a—(^2) + p (1 - am+1) yn q (    1

( 1    „ m +1 ¥l      n +1 ЛТ1

• ^{1    - a}₁    ^{- y} ) ^J

• 1    - y

  
  

The derivation of equation (9) is detailed [6] where P_c , denoting the collision probability, and y are given by:

Pc = 1 -(1 - т) N-1

y = Pc (1 - am+1)

Moreover, the transmission probability τ can be expressed as:

mn т = ZZ b^, i=0 j=0

f 1 - a m ^{+ 1} ( 1 - a

)f 1 -2 2 +1

Л ¹ - y

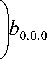
The transmission probability τ depends on the collision probability P _c and the probability a = a + Oicк , where a_L is the probability to sense the channel busy and find it occupied during one of the L packet transmission slots. ack denotes the probability to find the channel busy during one of the L_ack transmission slots. Then:

a L = L * P c * ( 1 - a )               (13)

*P * c

« ack

= L ack

N t ( 1 - т ) ^{N 1} ( 1 - a ) 1 - ( 1 - т ) N

From equations (9) to (14), we derive a system of nonlinear equations with a unique solution as explained in [2]. From this solution, the transmission probability τ can be obtained and henceforth all the state probabilities of the Markov chain modeling the beaconless IEEE 802.15.4 backoff can be determined.

• B.    Probabilistic Energy Consumption Bounds of the Unslotted CSMA/CA protocol

Once the state probabilities of the unslotted CSMA/CA backoff model are derived, we can focus on the energy consumption bounds of the considered scheme. These bounds will be expressed as the probability that the energy consumption within a node exceeds a certain value. They are obtained by deriving the energy consumption probability generating function (PGF) corresponding to the Z-transform of the energy consumption probability density function. Then, we use a paradigm largely inspired from [32] where the authors exploit the DTMC modeling the IEEE 802.11 backoff process to derive the generalized state transition diagram and therefore compute the service time PGF and the probabilistic delay bounds.

If we consider the beaconless IEEE 802.15.4, the energy consumption PGF is given by:

W ( Z ) H

2 ^{1 1} W о -1 z l =0

1 - I e ( Z )

2 ⁱW 0

² mb^ ' - I e ( Z ) ^z 2 m b

if i ^ m b — m 0

otherwise

We also define G ( Z ) , the PGF related to i sensing

fails due to the busy channel condition as:

E tot ( Z ) = £ P ( e tot = k Z^k          (15)

k = 0

i

G , ( Z ) = Z « ' ( S c ( Z ) )               (22)

k =0

Therefore, analogically to [32], the energy consumption PGF of the unslotted CSMA/CA scheme can be obtained as:

where E ^~ is the random variable representing the unslotted CSMA/CA energy consumption. To compute E ( Z ) , we derive the generalized state transition diagram from the DTMC given in Figure 1 such as we multiply on each edge between two states i and j the transition probability p ij by the quantity Z^k , where k is the energy consumed during the transition from state i to j . Thus, E ( Z ) is obtained from the signal transfer function of the generalized state transition diagram [32].

We introduce S(Z) , C(Z) , S C (Z) and I E (Z) the normalized energy consumption PGFs of respectively successful transmission, collision, sensing and idle-listening slots. As we compute E ( Z ) , all the energy consumption values must be discrete and expressed as a number of P i , where P i is the energy consumption during a slot time aUnitBackoffPeriod .

E_tot ( Z ) = (1 - P c ) S ( t ) £ ( P c C ( Z ) ) j (( 1 - a )

j = 0

m                   A j ^{+ 1}        n

Sc (Z)Z G. (Z)Hi (Z)|   + aZ (Pc C(Z))j i=0                  J          j=0

m

( 1 - a ) S c ( Z ) Z G i ( Z ) H ( Z )

i = 0

G m + 1 ( Z ) H m + 1 ( Z )

n + 1

m..

+1 ( 1 - a ) P c C ( Z ) S c ( Z ) Z G i ( Z ) H i ( Z ) |

V                             i = 0                   J

Therefore from the equation (15), we derive the energy consumption state probabilities as:

P t L + P r L ack , w

S ( Z ) = Z     ^Pi

Г P t L ⁺ P i L ack , w

C ( Z ) = Z    ^Pi

S c ( Z ) = Z

Г P 1

S ( Z ) = Z P i I = Z

P ( ~ ,.,

i d (E. (Z )> a k!     dZ

Hence, the energy consumption bounds are given by Po s( k ) , the probability that the consumed energy is greater than k :

P_lo s ( k ) = P ( E_tot >  k ) = ZZ P ( E_tot = k )         (25)

l = k

To validate the probabilistic energy consumption bounds given by equation (25), we use the Omnet++ network simulator [30]. Table 1 summarizes the parameters used in the simulation scenarios.

Let H (Z) be the PGF related to the energy consumption during the backoff process:

i

H i ( Z ) = П W k ( Z )             (20)

k = 0

Where:

Table 1. The Simulation Parameters used in Omnet

Parameter	Value
m 0	3
m b	5
n	3
L	80 slots
L ack	2 slots
Pi	712 (µW)
Pr	33.51 (mW)
Pt	31.32 (mW)

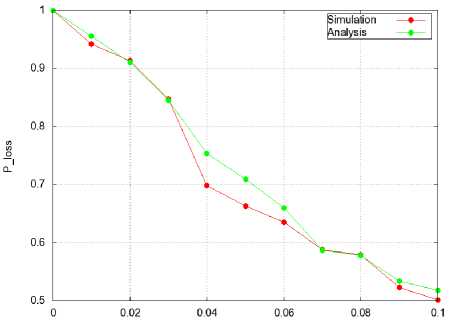
In Figure 2, we depict the energy consumption bounds given analytically by P_!oss ( k ) , the probability that the energy consumption exceeds a certain value k expressed as units of P_i . In Figure 2, the energy values on the x -axis are expressed in ( mw ) and are obtained by multiplying k by P_i . The results show that the energy consumption exceeds a certain value decreases with the energy consumption increase. Moreover, we notice in the same Figure 2 the accuracy of our analysis since the analytical results coincide with the simulations.

• C.    Approximated Average Energy Consumption

As stated in the previous paragraph, unslotted CSMA/CA energy consumption bounds are derived using the energy consumption PGF given by the equation (15). From this PGF , we can also derive the average energy consumption E using the following equation:

Energy consumption (in w)

Fig.2. Probabilistic Energy Consumption Bounds of Unslotted CSMA/CA derived as [6]:

m W i - 1 n                 m n

E O. = p -EEE ь . P c EE ь^ i =0 k =1 j =0                 i =0 j =0

m  L -1

n

⁺ P E ⁶ -1. L . j ^{+ 6} -1. L . j )

j =0

m L +1+ L ack

where P i , P sc , P t , P r , and P sp are the average energy consumption in idle-listening, channel-sensing, transmitting, receiving, and idle-queuing state respectively. Since P_sp is negligible, we consider the energy consumption in the idle state to be equal to 0. Hence, to derive the approximated average energy consumption, we adopt the following simplification as in [2] and [25]. For z ≥ 0, we have:

I m +1

- z

-------® z + 1 if z <<  1

1 - z

Then, if we consider the exact expression of the average energy consumption given by the equation (27), E is decomposed as the sum of E , E and E corresponding to the average energy consumption of all idle-listening, sensing and transmitting states respectively. Then. using the approximations ( 1 - y^{m + 1} ) / ( 1 - y ) ® y + 1 and ( 1 - a m ^{+ 1} ) / ( 1 - a ) ® a + 1. we have:

— Г d ( E ( Z ) ) )

tot

I     ^dZ     ) Z =1

Exact average or probabilistic energy consumption allow predicting accurate values of energy consumption within a sensor using the beaconless IEEE 802.15.4 medium access scheme. However, these exact expressions, despite their precision, cannot be easily implemented within sensor nodes for quality of service (QoS) or routing purposes. For instance, computing the average energy consumption within a sensor node based on the energy consumption Z-transform is not really possible due to the sensor nodes limited computation capabilities. Approximated expressions are in this case preferable and can be easily evaluated based on local estimated values. In the following, we derive simple nevertheless accurate approximated average energy consumption analysis of the unslotted CSMA/CA that we exploit in the next section to provide a cross layer scheme that enhances the native PEGASIS routing.

Hence according to the Figure 1 describing the unslotted CSMA/CA backoff, the average energy consumption of the unslotted CSMA/CA can also be

E - = P-

m  W i - • n

EEE ь - . k .j

i =0 k =1 j =0

= ^Pi⁶ 0.0.0 ^{( 1 +} y ) f W ⁰- ^{( 1 + 2 a )+( 1 +} « )

Esc = РУУЬо ,= Pcbo o(1 + y )(1 + a)

sc       sc               i ,0, j       sc 0,0,0

=0 j =0

m  L-1

E=P. EE(b-1. k.j+6 -2. k .j)+p-E(6-1. L.j i=0 k=0

m L +1+ ^L a_Ck

+ 6-2. L.j)+E E(Prb-1. k .j+ Pb-2k .j)

i=0

= ( 1 - a ² ) ( 1 + y ) 6 0.0.0 ( P t L + P i

+ L ack P r ( 1 - P c ) + P i P c )

Then E will be given by:

EtOt = Ei+ESC+Et(32)

Figures 3 and 4 depict exact, approximated and simulated average energy consumption values of the unslotted CSMA/CA using the simulation parameters of Table 1.

0 09

Approximated analysis Simulation

Exact analysis

s

0 08

E

0 06

0.05

0.04

2.5

!

3.5

Maximum CSMA backoff (m)

Fig.3. Average Energy Consumption of Unslotted CSMA/CA as a Function of m

In Figure 3, the average energy values are depicted as a function of m , the maximum number of CCA attempts per transmission ( N = 10, q = 0.8). In Figure 3(b), we fix m to 4, the default value of maxCSMABackoffs in the IEEE 802.15.4 standard. We depict the average values as a function of the number of stations N present in the network ( q = 0.2).

Both Figures 3 and 4 show that the approximated energy consumption values are very close to both exact and simulated values which illustrates the accuracy of the approximation used to derive the average energy consumption of the unslotted CSMA/CA.

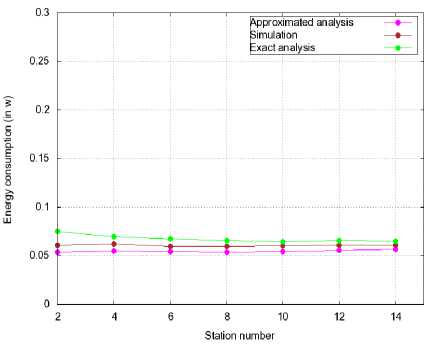
Fig.4. Average Energy Consumption of Unslotted CSMA/CA as a Function of N

IV. A Cross Layer Scheme to Enhance thE Native PEGASIS Routing

In this section, we propose to exploit the approximated average energy consumption of the unslotted CSMA/CA derived in the previous Section to enhance the behavior

of the native PEGASIS routing. Our new routing scheme is called Average Energy Enhanced-PEGASIS (AE2-PEGASIS). Our choice to enhance the native PEGASIS routing is motivated by the fact that PEGASIS outperforms several energy-efficient routing protocols.

Therefore, we briefly review the existing energy based routing schemes in particular the PEGASIS routing. Then, we present the basics of the AE2-PEGASIS and compare its performance to other routing solutions and mainly to the PEGASIS routing.

A. Energy Efficient Routing Solutions in WSNs

Several routing solutions were proposed in literature to efficiently manage the energy consumption in WSNs. Energy aware routing solutions can be divided into flat and hierarchical routing solutions. In the category of flat routing solutions, we find Sensor Protocols for Information via Negotiation (SPIN) [9] and Direct Diffusion (DD) [14] two data centric routing schemes proposed to reduce the amount of data exchanged in WSNs. SPIN uses ADV meta data packets to send a resume of the forthcoming data. Sensor nodes interested in receiving the announced data send a REQ packet. Upon the reception of REQ packets, DATA packets can therefore be transmitted using data aggregation. DD routing is another data centric routing for WSNs. With DD, the sink node defines an interest using a pair of (value, attribute) and broadcast it to the neighbors. When an interest is captured by a node, it is sent to the node's neighbors while keeping a copy in his buffer. A gradient is a response link to the node expending the interest. The sink can therefore send back the originating interest message to the source hence enforcing the path reliability. Gradient-Based Routing [27] is a slightly modified version of DD where the number of hops to the sink is broadcasted with the interest to retrieve the minimum number of nodes to the sink called the node's height. Gradient based routing can be considered as an energy aware routing since a sensor node increases its height when its energy level comes below a given threshold.

Energy aware routing [28] is an energy oriented routing scheme where the routing metric is computed based on the distance from the sender, the energy used to transmit/receive data in the network and the residual energy normalized by the initial energy. This routing scheme uses a multi path routing to avoid energy waste along the path to the sink node if a unique path is used.

Flat routing solutions show their limits when the network size becomes very large, hence, the hierarchical routing becomes more appropriate. Low Energy Adaptive Clustering Hierarchy (LEACH) [10] is a leading power saving hierarchical routing scheme. It selects cluster heads using round robin scheduling to ensure fair energy dissipation between the sensors in the network. LEACH executes in two phases. A set-up phase to select the future cluster heads and the steady state phase to exchange data in the network. Although LEACH efficiently reduces the energy consumption in the network, it presents some limitations. For instance, it supposes cluster heads can directly reach the sink nodes using high energy

transmissions.

Hybrid, Energy-Efficient, Distributed approach (HEED) [15] is another energy aware routing where cluster head election is based on the sensor nodes' residual energy and the nodes' degree. HEED aims to have a uniform distribution of cluster heads and cluster sizes. HEED do not specify which algorithm is used to ensure the communication between the sensors in the sink direction. Moreover, it does not perform any energy optimization within the cluster. The Threshold sensitive Energy Efficient sensor Network protocol (TEEN) [21] is a data centric hierarchical routing. With TEEN, a cluster-head broadcasting a hard threshold is used to indicate to the sensors when they should send their aggregated data. Despite its energy conservation, TEEN is not suited to applications requiring periodic data transmissions.

Finally, we consider the PEGASIS routing scheme [19] which is an improved version of the LEACH protocol. With PEGASIS, the communication is ensured through a chain construction between the sink and its furthest node. To construct this chain, the sensor nodes have a global knowledge of the network topology. Moreover, they all can directly reach the sink. Hence, the furthest sensor starts the chain construction hop by hop to the sink using a greedy algorithm such as at each step, the nearest neighbor is chosen as the next hop to the sink. Based on this chain, each node collects its data and sends it to its neighbor that proceeds to the aggregation of the received data with its own data and repeats the process again till reaching the sink. The main drawback of the existing routing schemes can be listed as follows:

• •    The energy consumption is computed after the emission/reception of each packet which may cause additional energy dissipation caused by this per packet evaluation.

• •    Energy aware routing solutions use physical layer based information (energy consumption of electrical components, signal emission/reception power, etc.).

• •    The MAC layer provides simpler energy consumption models which are not integrated at the network layer for routing purposes.

For all the above mentioned reasons, we propose in this paper to enhance the behavior of the native PEGASIS scheme by introducing a cross layer scheme called the Average Energy Enhanced-PEGASIS (AE2-PEGASIS) based on the average dissipated energy estimated at the MAC layer.

• B. The Average Energy Enhanced-PEGASIS (AE2-PEGASIS)

The key idea of our cross layer routing is to exploit the energy consumption analysis of the beaconless IEEE 802.15.4 medium access layer, done in Section 3 to enhance the native PEGASIS routing scheme. Hence, the A2E-PEGASIS is a cross layer routing that considers not only the distance when constructing the chain to the sink but also the dissipated energy within each node, evaluated at the MAC layer, through the path to the sink. The dissipated energy is evaluated based on the approximated average energy consumption derived by equation (32). Then, the dissipated energy at the MAC layer is periodically re-evaluated and broadcasted in the network as we explain below.

• a)    Energy dissipation estimation at the IEEE 802.15.4 MAC layer: To evaluate the energy dissipation at the IEEE 802.15.4 MAC layer, we use the approximated average energy consumption analysis done in Section III. Therefore, we consider the following notations:

o  Et (t) : The approximated average energy dissipated in the node Ci during the time interval [0..t].

o E ( t , tj_ j ) : The approximated average energy dissipated in the node Ci between time instants tj and tj__x ( i.e. between periods j and ( j - 1 ) ).

Hence, the average energy dissipated at each node C_i at the time instant t is given by:

k

E i kh ) = У, E i ( t j , t j - 1 )                (33)

j = 1

where:

E i ^{( t}j , t j - 1 ) = E tot * ^Npackets ^{( t}j , t j - 1 )         (34)

and E , given by the equation (32), is the approximated average energy consumed during the transmission of a sized L packet - L is determined in the equation (1)- and Npncttts^j , tj- 1) is the number of packets transmitted between time instants t and t .

• b)    Presentation of the AE2-PEGASIS scheme: The AE2-PEGASIS routing is largely based on the native PEGASIS scheme. For instance, it considers that all the sensor nodes can directly reach the sink.

Moreover, the algorithm assumes that, initially, all the sensor nodes have the same energy resource with heterogeneous traffic load. As a first step, AE2-PEGASIS constructs the chain to the sink in the same way as the native PEGASIS such as the furthest node triggers the chain construction by selecting at each hop its nearest neighbor. Periodically, at time instants t , each node C_i reevaluates its dissipated energy based on the equation (34) and broadcasts an Ener_Update message. Each node in the network receives the Ener_Update message and a new chain construction is triggered based on both the distance to the sink and the dissipated energy within each node. Hence, the dissipated energy values are refreshed in the network and each node computes a new cost to the sink as:

Cost ( C i , sink ) = 0 * dist ( C i , sink ) + в * E i ( t k ) with 0 + в = 1

Based on the equation (35), the node C* is elected as the root node that triggers a new chain reconstruction to the sink such as:

Cost (c *, sink) = min{Cost (C,, sink)}

A similar cost formula is used when a given node C_i along the route to the sink elects its successor C ^succ to the sink such as:

Cost(c,C,s"cc)=    min   {Cost(c,C, )}

X i i '   j eRemainingSet where Remaining_Set represents the set of sensor nodes, not attached to the chain, relating the node C* to the sink. Hence, with AE2-PEGASIS, we ensure that the energy dissipation in each node is primordial to determine how the information is routed in the network and whose nodes are in charge of aggregating and transmitting more data than the others based on their local traffic load. For instance, when considering only the distance as a cost to the sink, some intermediate nodes are heavy loaded and are very close to the sink node.

Hence, they have to aggregate and send more data to the sink. On the other hand, some other nodes near the furthest node, situated at the beginning of the chain, may have few data to transmit. Moreover, they perform few aggregation tasks given their position in the chain. Therefore, it becomes crucial to consider both the distance and the dissipated energy when constructing the route to the sink.

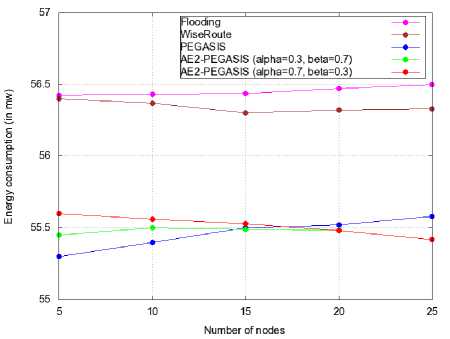
Fig.5. Comparison of AE2-PEGASIS to other Routing Schemes

To evaluate the performance of the AE2-PEGASIS scheme, we implement this solution under the Omnet++ simulator using the same simulation parameters as in Table 1. We compare the performance of AE2-PEGASIS, in terms of energy consumption, to other routing schemes such as flooding, Wiseroute [30] and the native PEGASIS as shown in Figure 5. For instance, the Wiseroute protocol is a simple flat routing solution implemented in Omnet, where all the sensor nodes construct a tree to the sink. Each node elects its next hop to the sink using the highest Received Signal Strength Indication (RSSI) among its neighbors based on the broadcasted messages received from its neighborhood.

The results in Figure 5 show that both PEGASIS and AE2-PEGASIS offer better energy consumption than the other routing schemes. This behavior is predictable since, as we said before, the PEGASIS routing offers better performance than other routing protocols such as LEACH or HEED. Moreover, if we compare AE2- PEGASIS to the native PEGASIS, we notice that for different values of (0, в)  , the PEGASIS routing offers better performance when the number of nodes in the network is very low. However, the AE2-PEGASIS performance improves as the number of sensors in the network increases. This behavior can be explained as follows:

• •    In low density networks, the distance between the sensor nodes is important. Hence, the cost values along the path to the sink are mainly based on the distance parameter since it predominates in the cost formula. In this case, we notice that the native PEGASIS performance is better than AE2-PEGASIS since the letter introduces a periodic exchange of Ener_Update messages.

• •    On the other hand, when the network density increases, the routes are more likely to be constructed based on the energy dissipated within the sensor nodes. Moreover, we notice that the whole network energy consumption decreases as the energy dissipation contribution (given by the parameter в ) in the cost evaluation becomes significant.

Hence, we conclude the efficiency of the AE2-PEGASIS routing for high density networks.

V. Conclusion

In this paper we proposed a comprehensive energy consumption study of unslotted CSMA/CA under unsaturated traffic conditions. In our analysis, we consider the DTMC modelling the beaconless IEEE 802.15.4 backoff process and we use the generalized Z-transforms to derive probabilistic energy consumption bounds of the unslotted CSMA/CA validated by simulation using the Omnet simulator. Despite their accuracy, the probabilistic energy consumption bounds cannot be easily used by the sensor nodes for QoS or routing purposes. This is due to the relatively complicated computation that should be done by the sensor node before deriving the P_loss values as illustrated in the equation (25). Then, as a second step of the energy consumption analysis, we proposed an approximated average energy consumption computation. With the approximated analysis, we obtain simple expressions of the energy consumption that can be used based on local

Energy Consumption Analysis and Cross Layer Routing estimated values. Simulations results showed the accuracy of our approximation. In the last part of the paper, we proposed a cross layer routing scheme that uses the approximated average energy computation at the IEEE 802.15.4 MAC layer to enhance the behavior of the native PEGASIS, a well-known hierarchical routing for wireless sensor networks. Our proposed routing scheme called A2E-PEGASIS outperforms existing routing schemes such as flooding or Wiseroute. Moreover, compared to the native PEGASIS, the AE2- PEGASIS benefits become significant as the number of nodes in the network increases and the overhead introduced by AE2-PEGASIS becomes negligible.