Performance Evaluation on the Effect of Combining DCT and LBP on Face Recognition System

Usually in the face recognition systems that the feature vector characterizing the face of an individual is extracted by using DCT coefficients or DCT coefficients in logarithm domain are considered (Weilong et al., (2004) and Haritha et al., (2012)). These methods are known as holistic matching methods. In this method, the whole face is represented as a D-dimensional vector. Due to the size of the dimensionality, the feature vector is further reduced by taking few DCT coefficients in each block. However, these methods are capable of considering the global (Macro) information of the face. But, they may miss the local information, such as the relations between the adjacent pixels in the face image. Hence to incorporate, the local information of the face in the feature vector, local matching methods, local binary patterns is more popular and efficient (Md jan Nordin et al., (2011), Hazim et al., (2007), Ziad et al., (2001), Zhao et al., (1999 and 2003), Conrad et al., (2003) and Satyanarayana et al., (2007 and 2009)).

To have an effective face recognition system we integrate the holistic methods with local matching methods by hybridization of LBP with DCT in feature vector extraction. Recently, there is some work reported in literature regarding the hybridization of LBP with DCT (Shoet et al., (2004), Weilong et al., (2004)). Hazim et al., (2007) has developed a face recognition system that combines discrete cosine transformation based local appearance face recognition technique with local binary pattern (LBP) representation of the face images. E.L.Aroussi et al., (2010) has proposed a face recognition method by considering discrete cosine transformation and local binary patterns. Pei-zhi Chen et al., (2010) has proposed a face recognition algorithm using discrete cosine transformation and local binary pattern for extracting the feature vector. In all these papers, they assumed that the feature vector follows a single Gaussian or a Gaussian mixture model.

In Gaussian mixture model the feature vector of each component in the face is symmetrically distributed with meso kurtic nature having infinite range. But in reality, the DCT coefficients after preprocessing with local binary patterns are having finite range and asymmetrically distributed with lepto or platy kurtic nature. Hence, to incorporate the realistic nature of the feature vector extracted through DCT coefficients with local binary patterns, it is needed to modify the GMM classifier by considering that the feature vector follows a doubly truncated multivariate Gaussian mixture model.

Very little work has been reported in literature regarding utilizing doubly truncated multivariate Gaussian mixture model for face recognition systems only at the works of Haritha et al., (2012). With this motivation, in this chapter, we develop and analyze a face recognition system that combines discrete cosine transformation based local appearance face recognition technique with local binary patterns using doubly truncated multivariate Gaussian mixture model and K-means or hierarchical clustering algorithm. This approach utilizes the local and global information and develops the face model for general statistical distribution. As a result of it, it improves the accuracy of the recognition system.

Here, the input is first transformed to the local binary pattern domain (Ojala et al., (2002)). The obtained local binary pattern image is divided into non-overlapping blocks. Then from each block the DCT coefficients are computed and feature vector is extracted. By using the Expectation-Maximization algorithm the model parameters are estimated. The initialization of the model parameters is done by using either K-means algorithm or hierarchical clustering algorithm and moment method of estimation. The face recognition system is developed with the likelihood function under Bayesian frame. The efficiency of the developed face recognition system is evaluated by conducting experimentation with JNTUK and Yale face image databases.

The paper is structured as follows. Section II summarizes feature extraction using DCT coefficients and local binary pattern, Section III summarizes modelling the feature vector and estimation of the parameters using EM algorithm, Section IV summarizes initialization of model parameters, Section V summarizes the face recognition algorithm, experimental results are given in Section VI, comparative study is presented in Section VII and finally, conclusions are presented in Section VIII.

• II.    FEATURE VECTOR EXTRACTION USING DCT COEFFICIENTS AND LOCAL BINARY PATTERN

In this section, we briefly discuss the feature vector extraction utilizing LBP with DCT. The discrete cosine transform is capable of de-noising the image and LBP captures the micro level information of face features. The integration of LBP with DCT will provide efficient extraction of feature vector in the recognition system. Since, it combines both macro and micro level information of each individual face.

The local binary pattern (LBP) operator converts each pixel intensity with a decimal number by capturing local structure around each pixel. By subtracting the center pixel value for each pixel is compared with it’s 3x3 neighbourhood eight pixel values. The negative values are coded with zero and all other values are with one. As a result of it, for each pixel a binary number is obtained by concatenating all these binary values in a clockwise direction. Usually, the process starts from top left neighbour. The associated decimal values that are generated by binary number are used for labelling the pixels. The derived binary numbers are called LBP’s (Huang et al., (2011) and Chi et al., (2007)).

The basic drawback of the LBP operator is that its small 3 x 3 neighbourhood cannot capture dominant features with large-scale structures. To deal with the texture at different scales, the operator was generalized to use neighbourhoods of different sizes (Ojala et al., (2002)). A local neighbourhood is a set of sampling points evenly spaced on a circle, which is centered at the pixel to be labelled. The sampling points that do not fall within the pixels are interpolated using bilinear interpolation thus allowing for any radius and any number of sampling points in the neighbourhood. Given a pixel at (x c , y c ), the resulting LBP is expressed in decimal form as

ЬВ^яСХс.Ус): £s(lp- iJZl»

? = D (1)

where, corresponds to the gray value of the center pixel (x c , y c ), refers to gray values of P equally spaced pixels on a circle of radius R, and s defines a thresholding function as

M f L I/ X > 0 sw = ; .

( 0, otherwise

The basic LBP operator is invariant to monotonic grayscale transformations, which preserve pixel intensity order in the local neighbourhoods. The operator LBP (P,R) produces 2 ^P different output values, corresponding to 2 ^P different binary patterns formed by P pixels in the neighbourhood. The DCT features extracted from LBP-images have lower ratio than the ones extracted from pixel intensity values.

The combined algorithm for feature vector extraction implemented as follows: The input image is first transformed to the LBP-domain. The obtained LBP-image is then divided into non-overlapping blocks of 8x8 pixels resolution. One each block the DCT is applied and the same feature extraction steps are performed as in the local appearance face recognition approach. A detected and normalized face image is divided into blocks of 8x8 pixels size. Then, the DCT is applied on each block. The obtained DCT coefficients are ordered using zig-zag manner. From the ordered coefficients, 15 of them are selected according to a feature selection strategy, and then normalized resulting in a D-dimensional local feature vector. These extracted local features are then concatenated to represent the entire face image.

III. MODELING THE FEATURE VECTOR AND ESTIMATION OF THE PARAMETERS USING

EM ALGORITHM

In this section, we briefly discuss the probability distribution (model) used for characterizing the feature vector of the face recognition system. The feature vector consisting of DCT coefficients after applying LBP on face image of each individual face, it can be modelled by a suitable probability distribution such that the characteristics of the feature vector should match with the statistical theoretical characteristics of the distribution. Here, also it is assumed that the feature vector of each individual face follows a K-component mixture distribution. In each component the feature vector is having finite range and it can be assumed to follow a doubly truncated Gaussian distribution. This in turn implies that the feature vector of each individual face obtained through DCT coefficients after applying LBP can be characterized by a K-component doubly truncated multivariate Gaussian mixture model. The joint probability density function of the feature vector associated with each individual face is

And

Where, and ^XM are lower and upper truncation points respectively. The degree of truncation is (A) and (1-B). If is replaced by -^or x_M 6у 00 the distribution is singly truncated from above, or below, respectively. The mean of ■': is

(0(xz) - 0(xv) ) is the standard normal area and , XM are the lower and upper truncated points of the feature vectors (Sailaja et al., (2010)).

The variance of DCT coefficients after applying LBP of each face is

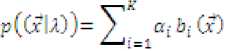
The mixture weights aL-, i = 1,2,... satisfy the constraints

here, х = (xfJf=tiJ is a D dimensional random vector denoting the feature vector bi(x): i=1,2,…,K are the component densities and the value of (the feature vector) below some value of ^ and above some value of ^M does not exist. Hence, the density function of is to be adjusted by truncating the random vector. The probability density function of doubly truncated multivariate Gaussian distribution is

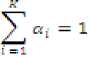
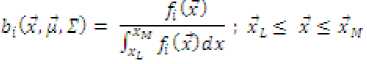
The truncation points and хлг are to be estimated from the observed feature vectors of each face image. The FDTGM density is parameterized by the mean vector, Co-variance matrix and mixture weights from all components densities. The parameters are collectively

5 —                 • represented byA = IGp^ZfJ; i=1,2,…,K. Here, we use diagonal covariance matrix for our face model.

Where,

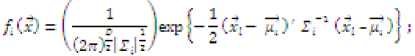
Therefore

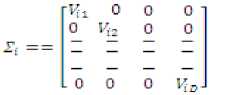
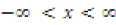
As a result of this, the 0iVC_t,U, reduces to

is the probability density function of a D dimensional Gaussian variate, ■^ is the mean vector, is the covariance matrix.

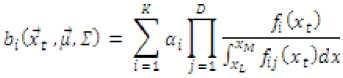
Therefore

b^.u.Z) =

№

В —A

Where, fi^ is as defined in equation (3), and A, B are given by,

Where,

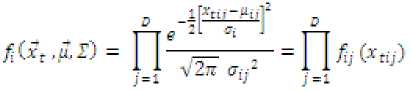
and,

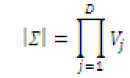
For developing the face recognition model it is needed to estimate the parameters of the model. For estimating the parameters in the model we consider the EM algorithm which maximizes the expected likelihood function of the model for a sequence of ‘t’ training vectors (r_t = (x_t х_г ... x_t)).

The likelihood function of the DTMGMM is

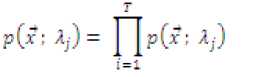
where, p(^ А})

is given in equation (2).

Using the Expectation-Maximization algorithm, the model parameters are estimated. The updated equations of the parameters for each feature vector are as follows:

a?*1 = ^ ^pGR-^)

z;,^ pfrM + zu ^ 2^ =4 = pGI^-^)

And с ЕГ=1рО1^гЛ)               (11)

Where, c is given by

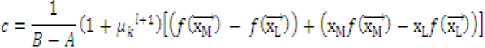
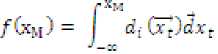
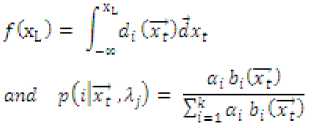
• IV.    INITIALIZATION OF MODEL PARAMETERS

The likelihood function contains the number of components K which can be determined by using the K-means algorithm or hierarchical clustering algorithm. The K-means algorithm and hierarchical clustering algorithm can be utilized for segmenting each individual face image dataset consisting of facial feature vector namely, DCT coefficients after applying LBP using the method.

After obtaining the final values of the number of clusters K, we are clustering the data set into K groups by either K-means algorithm or hierarchical clustering algorithm. The EM algorithm can be applied for refining the parameters with updated equations. To utilize the EM algorithm we have to initialize the parameters ^«i.Ui.a^.i = [1... .K}. XM and XL are estimated with the values of the maximum and the minimum values of each element in the feature vector respectively. The initial values of ar can be taken a,- = ^                                                (13)

The initial estimates of a^,u^ cind tjf of the i ^th component is obtained using the method A.C. Cohen et al., (1950). The initial estimates of the parameters are P: ~ -^-r = l^ is the sample mean of the i^th component and^=V^^1 (^-^) is the standard deviation of the i ^th component. We obtain the final refined estimates of the parameters through the updated equations of the EM algorithm given in section 3.

• V.    FACE RECOGNITION SYSTEM

Face recognition means recognizing the person from a group of H persons. The Figure 1 describes the face recognition system based on DTMGMM and DCT after applying LBP.

Face recognition system is usually viewed as a two class classification problem and matching. Here, two classes are claimed identity or to an imposter. The Bayesian classifier based on doubly truncated multivariate Gaussian mixture model is utilized. For each person two types of models are obtained. The first one is for the distribution of the training face for that particular person. The second is for the distribution of training feature vector for all training faces. This is refered as a generic model or a world model or a universal background model (Concord Sanderson et al., (2005)).

Let us consider our face recognition system has to detect the correct face with our existing database. Here, we are given with a face image and a claim that this face belongs to a particular person C to classify the face a set of feature vectors ** — ^i^i=i extracted using the computational methodology of feature vector extraction discussed in section 2. By assuming that the likelihood of the face belonging to person C is found with

ZtoUc) = nP(xJAc)

Where,

And

Л = {а^ра,}*-!and b(x: UpIO is a D-dimensional doubly truncated multivariate Gaussian density function. ^ c is the parameter set for person C, K is the number of components in the model and gl is the weight of ith component such that Sf=l “i = 1 and V:: Qi > 0

The universal background model is used to find the likelihood of the face belonging to an imposter. ^C^l-^geiwricj is the likelihood function of the claimant computed based on the parameter set ^5»ns-ric . The is ^ genericcomputed by considering all faces in the dataset and obtaining the average values of the parameters. The decision on the face belonging to the person C is found using

Oto = llogLCmj-logLCrU^rJI

The final decision for given face is then reached as follows. Given a threshold t the face is classified as belonging to person C, when о to) is greater than or equal to t. It is classified as belonging to an imposter when о to) is less than t.

For a given set of training vector z c for all faces in the database and ^5»n»rir are computed by using the updated equations for the model parameters discussed in section 3 and using the initial estimates of the model parameters obtained by using either K-means algorithm or hierarchical clustering algorithm discussed in section 4.

• VI.    EXPERIMENTATION AND RESULTS

  The performance of the develop algorithms are evaluated by considering the face images taken from two databases namely, JNTUK face database and Yale face database. The JNTUK and Yale face database consisting of 120 faces (Satyanarayana et al., (2008) and Qian et al., (2007)). Sample of 20 person’s images from JNTUK database is shown in Figure.2.

For initialization of the model parameters with K-means algorithm, a sample histogram of the face image is drawn and counted the number of peaks and found K=3. Then K-means algorithm is used to divide the feature vectors of blocks into K groups. For initialization with hierarchical clustering we divide the feature vectors of all blocks in the face image into K number of groups using hierarchical clustering algorithm. With hierarchical clustering also we find K=3.

Figure 2. sample images from JNTUK database

ORIGINAL IMAGES FROM JNTUK DATABASE

Figure 3. row1 and row3 are the original images from JNTUK and YALE databases. row2 and row4 are the images after applying local binary pattern for the face images of row1 and row3

After dividing the observations into three categories by both the methods and assuming that the feature vector of the whole face image follows a three component finite doubly truncated multivariate Gaussian mixture model. The initial estimates of the model parameters Of'К '5 are obtained by using the method discussed in section 4 with K-means algorithm and hierarchical clustering algorithm.

With these initial estimates the refined estimates of the model parameters are obtained by using the updated equations of the EM algorithm and MATLAB code as discussed in section 3. Substituting the refined estimates of the model parameters, the joint probability density function of each face image is obtained for all faces in the database.

By considering all the feature vectors of all faces in the database the generic model for any face is also obtained by using the initial estimates and the EM algorithm as discussed in sections 4 and 3 respectively. The parameters of the generic model are stored under the parametric sets ^SSTMTLC . The individual face image model parameters are stored with the parametric set , i= 1, 2,. ..N. N is the number of face images in the database.

Using the face recognition system discussed in section 5, the recognition rates of each database is computed for different threshold values of t in (0, 1). The false rejection rate, false acceptance rate and half total error rate for each threshold are computed using the formula’s given by (Conrad Sanderson et al. (2002, 2003 and 2005)).

number of FA s

РДР — __________________^_______________ number of imposeter face presentations number of PR's

frr = —L—----гт— number of true face presentations

Where, FA indicates the false acceptance and FR indicates the false rejection

FAR + FRR Half total error rate = HTER = ---------

True positive rate = 1 — FRR

The HTER is a special case of Decision Cost function and is often known as equal error rate when the system is adjusted. Plotting the FAR and true positive rate for different threshold values, the ROC curves for both the databases are obtained and are shown in Figures 4 and 5.

Using the ROC curves, the optimal threshold value ‘t’ for each database is obtained. These threshold values are used for effective implementations of the face recognition system.

TABLE I. RECOGNITION RATES

Database	Recognition system	HTER	Recognition rate
JNTU	DTMGMM with K-means	2.35	97.8±0.4
	DTMGMM with hierarchical	1.84	98.82±0.4
Yale	DTMGMM with K-means	2.5	97.5±0.3
	DTMGMM with hierarchical	2.08	98.33±0.4

Table 1 shows the values of HTER and recognition rates of both face recognition systems. The Figures 4 and 5 show the comparison of ROC curves for both the proposed systems and also for both databases respectively.

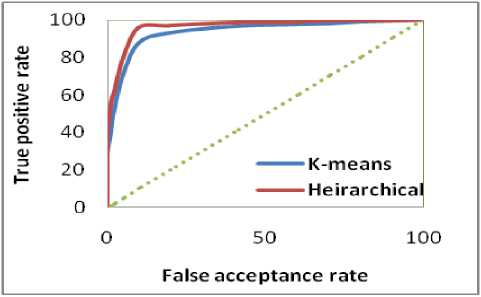
Figure 4. ROC curve for JNUTK database

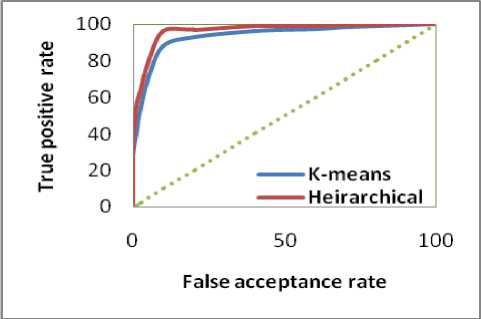
Figure 5. ROC curve for Yale Database

Using the method discussed in section 2, the feature vectors consisting of DCT coefficients after applying LBP for each face image and for both the databases are computed. For each image calculated of feature vectors of blocks are divided into K groups representing the different face features like neck, nose, ears, eyes, etc. Two approaches are adopted for determining the value of K and initialization of the parameters as discussed in section 4.

From Table 1, Figures 4 and 5, it is observed that the proposed algorithm identifies with 97.8% and 97.5% for JNTUK and Yale databases correctly. From the ROC curves, it is observed that the proposed models perform better. It is further observed that even under DCT + local binary pattern of the face recognition system based on DTMGMM using hierarchical clustering is better than that of K-means algorithm for both databases namely, JNTUK and Yale.

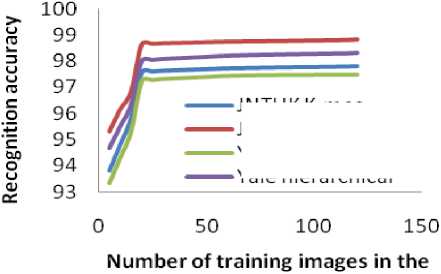
The efficiency of the developed system with respective to the size of the database is also studied by varying the number of face images from 5 to 120 available in JNTUK database. The HTER and recognition rates for different sizes of the databases from JNTUK database are computed and shown in Table 2. Figure 6 shows the relationships between the number of faces in the database and the performance measures of the system.

From Table 2 and Figure 6, it is observed that the recognition rate of both the systems increase when the number of faces in the database increases. The recognition rate increases upto a size of 20 images and stabilize there after. This may be due to the more number of observations available for training the recognition system and efficiency of estimating the model parameters increases with observations. However, the recognition rate is above 93% for all sizes and it stabilizes after a size of 20 faces. This indicates that the face recognition system is suitable for small and large databases.

JNTUK К-means JNTUK hierarchical

Yale K-means

Yale hierarchical database

Figure 6. Recognition rate for different databases using DTMGMM

TABLE II. THE VALUES OF HTER AND RECOGNITION RATES FOR DIFFERENT DATABASES USING dtmgmm

Total number of images	K-means algorithm				Hierarchical clustering algorithm
	JNTUK		Yale		JNTUK		Yale
	HTER	Recognition rate	HTER	Recognition rate	HTER	Recognition rate	HTER	Recognition rate
5	5.95	93.8	3.832	93.33	3.748	95.33	4.25	94.667
10	5.584	94.8	3.083	94.3	2.66	96.167	4.167	95.5
15	4.75	95.8	3.333	95.3	2.5	96.833	3.833	96.33
20	2.833	96.57	3.613	96.25	2.084	97.64	2.66	97.02
25	2.666	97.6	3.667	97.29	2.583	98.66	3.25	98.06
30	2.915	97.63	3.333	97.33	2.35	98.68	2.084	98.1
40	2.833	97.66	2.915	97.37	2.5	98.7	2.66	98.14
50	2.35	97.69	2.084	97.41	2.583	98.72	2.5	98.18
60	2.35	97.72	2.583	97.45	2.6	98.74	2.583	98.22
80	2.66	97.76	2.5	97.48	2.35	98.77	2.66	98.27
100	2.35	97.78	2.6	97.49	2.6	98.8	2.583	98.31
110	2.833	97.79	2.5	97.495	2.583	98.812	2.5	98.32
120	2.35	97.8	2.5	97.5	1.838	98.824	2.084	98.33

TABLE III. r ECOGNITION SYSTEMS OF DIFFERENT FACE RECOGNITION SYSTEMS

Database	Recognition system	HTER	Recognition rate
JNTUK	GMM and K-means under DCT	5.5834	88.33±1.5
	GMM and hierarchical under DCT	4.75	90±1.3
	GMM and K-means under logarithm DCT	5.5834	90.83±1.3
	GMM and hierarchical under logarithm DCT	5.165	91.67±1.2
	GMM and K-means under DCT + LBP	5.1665	91.667±1.4
	GMM and hierarchical under DCT + LBP	4.75	92.5±1.1
	DTMGMM and K-means under DCT	3.7484	96.7±1.3
	DTMGMM and hierarchical under DCT	3.3333	97.5±0.9
	DTMGMM and K-means under logarithm DCT	2.66	97.18±0.8
	DTMGMM and hierarchical under logarithm DCT	2.0835	98.33±0.7
	DTMGMM and K-means under DCT + LBP	2.35	97.8±0.4
	DTMGMM and hierarchical under DCT+LBP	1.8377	98.824±0.4
Yale	GMM and K-means under DCT	6	87.5 ±2.1
	GMM and hierarchical under DCT	5.1667	89.17±1.8
	GMM and K-means under logarithm DCT	5.95	90.1 ±1.9
	GMM and hierarchical under logarithm DCT	5.4665	91.07±1.8
	GMM and K-means under DCT + LBP	5.583	90.833±1.7
	GMM and hierarchical under DCT + LBP	5	92±1.6
	DTMGMM and K-means under DCT	4.1667	95.83±1.2
	DTMGMM and hierarchical under DCT	3.749	96.93±0.8
	DTMGMM and K-means under logarithm DCT	2.0835	96.67±0.7
	DTMGMM and hierarchical under logarithm DCT	2.5	97.5±0.9
	DTMGMM and K-means under DCT + LBP	2.5	97.5±0.3
	DTMGMM and hierarchical under DCT+LBP	2.084	98.33±0.4

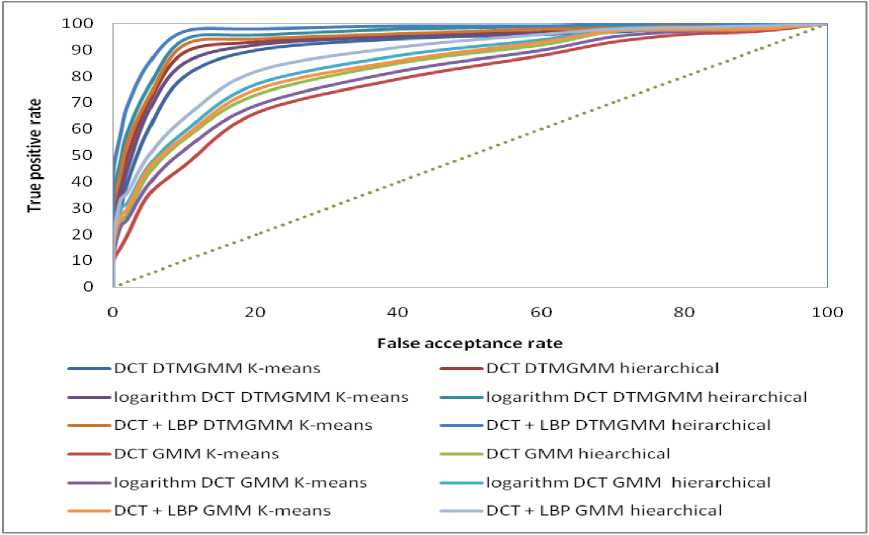
Figure 7. ROC curve for DCT, DCT in logarithm domain and DCT+LBP using DTMGMM for JNTUK

From the above discussions it is observed that the face recognition system with doubly truncated multivariate Gaussian mixture model with hierarchical clustering algorithm is more efficient compared to that of doubly truncated multivariate Gaussian mixture model with K-means and face recognition system with GMM

• VII.    Comparative study

In this section a comparative study of the developed face recognition system based on DTMGMM and K-means or hierarchical clustering algorithms with DCT + LBP domain with that of systems developed using DCT, DCT under logarithm domain and the face recognition systems based on GMM with K-means or hierarchical clustering under DCT domain, logarithm DCT and DCT + LBP domain is carried.

Table 3 presents the half error rate and recognition rates with their confidence intervals for the face recognition system of (i) DTMGMM and K-means under DCT + LBP, (ii) DTMGMM and hierarchical under DCT + LBP, (iii) DTMGMM and K-means under logarithm DCT domain, (iv) DTMGMM and hierarchical under logarithm DCT domain, (v) DTMGMM and K-means under DCT, (vi) DTMGMM and hierarchical under DCT, (vii) GMM and K-means under DCT + LBP and (viii) GMM and hierarchical under DCT + LBP (ix) GMM and K-means under logarithm DCT domain, (x) GMM and hierarchical under logarithm DCT domain, (xi) GMM and K-means under DCT and (xii) GMM and hierarchical under DCT for JNTU database and Yale database.

From Table 3, it is observed that the recognition rate of the face recognition system based on DTMGMM and hierarchical clustering under DCT+LBP is having 98.824% with confidence interval of 0.4 and it is much superior than other face recognition models given in Table 3. It is also observed that for the face recognition systems based on both DTMGMM and GMM are having higher recognition rates for the feature vector considered with DCT+LBP than that of DCT with logarithmic domain and DCT without logarithmic domain. It clearly shows that the face recognition system using DTMGMM is having nearly 9% improvement compared to the face recognition system using GMM for both databases. This clearly shows the face recognition system can be improved with a higher recognition rate by adopting DCT+LBP and normalize the image capturing conditions.

The Figure 7 shows the ROC curves of the face recognition systems based on the Table 3 JNTUK data. From Figure 7, it is observed that the face recognition system based on DTMGMM with hierarchical under DCT+LBP is better compared to other face recognition systems. It also observed that the face recognition system based on DTMGMM is having better performance compared to the face recognition systems based on GMM. It also shows that the face recognition systems based on DTMGMM successfully identifies the claimant’s face. All ROC curves shown in figure 6 are above the diagonal line indicate that all the face recognition systems are having good recognition rates. However, the face recognition system under DCT+LBP domain performs better than that of other systems because the proposed system minimizes the effect of illumination on the face image.

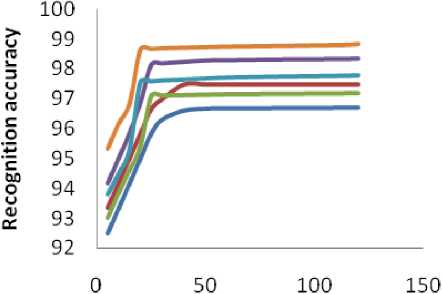
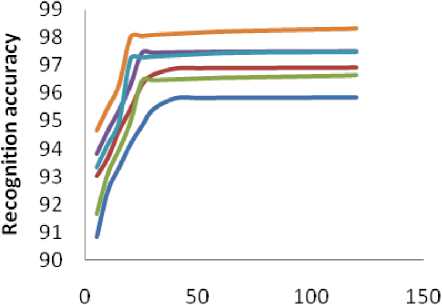
A comparative study on number of images in the database and the recognition rates of the systems is also carried to study the effect of size of the database on the performance of the face recognition system. Figure 8 and Figure 9 show the relationships between recognition rate and the number of images in JNTUK and Yale databases.

Number of training images in the database

^— DCT K-means

^^— DCT hierarchical

^^— logarithm DCT K-means logarithm DCT hierarchical DCT +LBP K-means

— DCT + LBP hierarchical

Figure 8. Recognition rate for DCT, logarithm DCT and DCT+LBP using DTMGMM for JNTUK database

Numberof training images in the database DCT K-means

DCT hierarchical logarithm DCT K-means logarithm DCT hierarchical DCT+LBP K-means

Figure 9. ROC curve for DCT, logarithm DCT and DCT+LBP using DTMGMM for Yale database

From the Figures 8 and 9, it is observed that the face recognition system with DCT+LBP domain is having better recognition compared to the other face recognition systems for both Yale and JNTUK databases. For the face recogntion system using DCT domain, the recogniton rate stabilizes after 30 images in the database and for the face recogniton system using DCT in logarithm domain stabilizes after 25 images, whereas, for the face recogntion system using DCT+LBP stabilizes after 20 images. This feature has a significant influence on the performance of the face recognition systems, since the system performance is dependent on the size of the systems. Here also it is observed that the face recognition systems using hierarchical clustering algorithm is having better recognition rate compared to the face recognition system using K-means algorithm for both JNTUK and Yale databases.

• VIII.    conclusions

A face recognition system based on doubly truncated multivariate Gaussian mixture model with DCT and LBP is developed and analyzed. DCT and DCT under logarithm domain are capable of considering the global (macro) information of the face. But, they may miss the local information, such as the relations between the adjacent pixels in the face image. Hence, to incorporate, the local information of the face in the feature vector, local binary patterns is considered. Here, the input image is first transformed to the local binary pattern image. The obtained local binary patterns image is divided into a number of non-overlapping blocks. From each block the DCT coefficients are computed and feature vector is extracted. The feature vector of the DCT coefficients after applying LBP of the whole face image follows a doubly truncated multivariate Gaussian mixture model.

By using the Expectation-Maximization algorithm the model parameters are estimated. The initialization of the model parameters is done by using either K-means algorithm or hierarchical clustering algorithm and moment method of estimation. A face recognition algorithm with maximum likelihood under Bayesian frame using threshold for the absolute difference between the estimated likelihoods of claimants and imposters is developed and analyzed.

The efficiency of the developed face recognition system is evaluated by conducting experimentation with face images collected from JNTUK and Yale databases. The performance measures like half total error rate, recognition rates are computed along with plotting the ROC curves. It is observed that for the face recognition systems based on DTMGMM are having higher recognition rates for the feature vector considered with DCT+LBP than that of DCT with logarithmic domain and DCT. It is observed that the face recognition system using DTMGMM is having nearly 9% improvement. This shows that the face recognition system can be improved with a higher recognition rate by adopting DCT+LBP and normalize the image capturing conditions.

International Journal of Information Technology and Knowledge Management , Volume2, No. 2, pp. 475-48, 2010.

• [18]    Ch. Satyanarayana, D. M. Potukuchi and L. Pratap Reddy, “Performance Incremental training method for face Recognition using PCA”, Springer, proceeding of the international journal of real image processing , vol. no:1, No:4, pp. 311-327, 2007.

• [19]    Ch. Satyanarayana, D. Haritha, D. Neelima and B. Kiran kumar, “Dimensionality Reduction of Covariance matrix in PCA for Face Recognition”, Proceesings of the International conference on Advances in Mathematics: Historical Developments and Engineering Applications (ICAM 2007) , pp: 400-412, 2007.

• [20]    Ch. Satyanarayana, D. Haritha, P. Sammulal and L. Pratap Reddy, “updation of face space for face recognition using PCA”, Proceedings of the international conference on RF & signal processing system (RSPS-08) , vol.1, pp. 195-202, 2008.

• [21]    Ch. Satyanarayana, D. Haritha, P. Sammulal and L. Pratap Reddy, “ Incremental training method for face Recognition using PCA”, proceeding of the international journal of Information processing , vol No: 3 No:1 pp: 13-23, 2009.

• [22]    Ch. Satyanarayana, PVRD. Prasad, G. Mallikarjuna Rao, D. Haritha, L. Pratap Reddy, “ A Comparative performance evaluation using PCA for Face Recognition”, proceeding of the international

  journal of Science & Technology , vol. no:4, No:4 , pp. 8-16,2008.

• [23]    J. Short, J. Kittler, and K. Messer, “A comparison of photometric normalisation algorithm for face verification”, Proc. Int’l Conf. AFGR , pp:254-259, 2004.

• [24]    Weilong chen, Meng Joo Er and Shiqian Wu, “ Illumination Compensation and Normalization Using Logarithm and Discrete Cosine Transform”, 8^th international conference on Control, Automation, Robotics and vision Kunming, IEEE , 2004.

• [25]    Xudong Xie and Kin-Man Lam, “An efficient illumination normalization method for face recognition”. Pattern Recognition Letters 27 , pp. 609–617, 2006.

• [26]    W. Zhao and R. Chellappa, “Robust Face Recognition Using symmetric Shape-from-Shading”, Technical report , Center for Automation Research Univ. of Maryland, 1999.

• [27]    W. Zhao, R. Chellappa, and A. Rosenfeld, ”Face Recognition: A literature survey”, ACM Computing surveys , vol.35, pp.399-458, 2003.

• [28]    M. Ziad M. Hafed and Martin D. Levine, “Face Recognition using Discrete Cosine Transform”, Proc. International Journal of Computer Vision , Vol. 43(3), pp. 167–188, 2001.

D. Haritha is Assistant Professor in Computer science and Engineering Department at Jawaharlal Nehru Technological University Kakinada. She has 12+ years of experience. She guided 30 M.Tech students and 15 MCA students for their project. Her research interest is on image processing, Data structures and networking. She published 5 research papers in international journals. She published 3 research papers in international conferences.

Dr. K. Srinivasa Rao is professor and chairman of P.G. Board of studies, Andhra University. He published 108 papers in reputed national and international journals. He guided 30 students for their Ph.D. degrees in 6 disciplines. He is the chief editor of journal of ISPS. He is the fellow of AP Academy of sciences. His current research interests are Data-mining, Stostatic modeling, Image Processing and Statistical Signal Processing.

Dr. Ch. Satyanarayana is Associate Professor in Computer science and Engineering Department at Jawaharlal Nehru Technological University Kakinada. He has 13 years of experience. His area of interest is on Image processing, Database Management Systems, Speech Recognition, Pattern recognition and network security. He guided more than 78 M.Tech projects and 56 MCA projects. He published 25 research papers in international journals. He published 35 research papers in international conferences.