Performance framework for HPC applications on homogeneous computing platform

Published Online August 2019 in MECS

The parallel computing model is introduced to solve large scale HPC applications. HPC rely on several computers to perform complex computations; therefore we can accomplish improved performance outcomes. On multi computer both task and data parallelism is a prerequisite to achieve the greatest performance results. GPUs are developed gradually to work on data parallelism. Most of the HPC applications are developed in scientific and engineering fields, which lead to the incorporation of HPC accelerators. Hybrid programming is the combination of different programming models to work on parallel applications. Parallel programming model makes uses of OpenMP, MPI and CUDA to solve complex problems [15]. Hybrid programming model provides a number of possible benefits such as first it analyzes the program and specifies the target platform to handle the threads to communicate. Communication and computation overlap is another benefit where few threads will be managed on communications and others will concentrate on the computation. By using Hybrid Programming model the work will be assigned to multiple GPU threads by CPU which results in better performance. Shifting from homogeneous to heterogeneous (CPUs+GPUs) cluster will have additional overhead of partitioning the workload and communication between CPUs and GPUs.

In this work, we are proposing a framework that uses an analytical model to predict asymmetric work load division between CPUs and GPUs based on its computation capabilities and its data transfer rate. The framework is built on three programming models i.e MPI, OpenMP and CUDA. The hybrid programming model uses cudaMemcpyAsync functions to transfer computation from CPU to GPU and vice-versa, there by come-across from the MPI send/receive overhead. Also framework uses pinned memory technique to overcome the overhead of data transfer latency between CPU and

GPU. To test our framework we have considered HPC applications like dynamic computations of N random vectors additions and saxpy applications. We have evaluated the performance of these applications on homogeneous platform one with NVIDIA TESLA M2075 and other nodes with two NVIDIA QUADRO K2000 on each node of a cluster.

In case of dynamic computations of N random vectors addition HPC application, we have achieved performance improvement of 76.06% on homogeneous platform with NVIDIA TESLA M2075 and 84.11% on homogeneous platform with two NVIDIA QUADRO K2000 on an each nodes of a cluster, with respect to application executed on Simplice Dogface performance model.

In case of saxypy applications with pinned memory technique, we have obtained on average of 33.83% on homogeneous platform with NVIDIA TESLA M2075 and 39.00% on homogeneous platform with two NVIDIA QUADRO K2000 on each nodes of a cluster, performance improvement over pagable technique.

The rest of the paper is structured as follows. Section 2 brief about related work with respect to hybrid programming models. Section 3 explains proposed framework design. Section 4 details about experiments and results. Section 5 presents conclusion.

• II.    Related Works

In this section, we describe the work accomplished so far in the area of homogeneous computing using hybrid programming model on CPU-GPU platform.

N.P. Karunadasa and D. N. Ranasingh [1] had demonstrated Accelerating High Performance Applications with CUDA and MPI. They find a few factors which improve application performance with GPUs. Among them the number of GPU cores is one of the important factors, and another factor is core specific data processing using adequate number of registers. Authors examined MPI and CUDA programming method with Strassen and Conjugate Gradient algorithm. They have demonstrated that Strassen algorithm works effectively in comparison with the Conjugate Gradient method. In our work, we have considered hybrid programming models such as OpenMP,MPI and CUDA with pinned memory technique to achieve better performance on HPC applications.

Qing-kui Chen and Jia-kang Zhang [2] had demonstrated the use of MPI and CUDA to build simple stream processor cluster system with CPU + GPU using the hybrid parallel computing programming environment (HPCPE). They used hybrid programming technologies to create a parallel computing environment. They considered CPU as stream processor cluster system and GPU as central calculating tasks on each node. But in our work we have considered the CPU to compute part of computation, to obtain better performance by proper utilization of the available CPU and GPU resources.

Linpack) benchmark on CPU-GPU nodes on a heterogeneous cluster. In their way authors distributed the workload based on the compute power of CPU/GPU nodes across the cluster. They also handled multi GPU configurations by using techniques such as process grid reordering to reduce MPI communication, while ensuring load balance across nodes. Authors present detailed analysis of performance, efficiency, and scalability of their hybrid HPL design across different clusters with different configurations. In our work, we are going to apply a novel analytic workload division strategy, where small amount of workload is assigned to a CPU and remaining work load will be allotted to GPU.

Takuro Udagawa and Masakazu Sekijima [4] proposed a new method to balance the workload between CPUs and GPUs. Their proposed method is built on formulating and observing workloads for statically distributing the work. Authors succeeded in utilizing processors more efficiently and accelerating simulation using NAMD. It gave 20.7% improvement compared to CPU optimal code. Their proposed method is demonstrated using molecular dynamics (MD) simulation. In our work, an analytic work load division technique with hybrid programming model was utilized to achieve performance improvement on NVIDIA TESLA M2075 and NVIDIA QUADRO K 2000 respectively for N dynamic vector addition.

Simplice Donfack et.al [5] present effective hybrid CPU/GPU approaches that is portable. It dynamically and efficiently balances the workload between the CPUs and the GPU. Authors also examined data transfer bottleneck between CPU and GPU. In their approach, the amount of initial work assigned to the CPU before execution is determined by the theoretical model. Then, they dynamically balanced the workload during execution in order to maintain load balance. But in our modeling strategies, nominal amount of work load will be placed on the CPU and remaining work load will be assigned to GPU.

Lu, Fengshun et. al [14] utilized two parallel programming models of MPI+CUDA and MPI+OpenMP+CUDA to parallel three kernels of NAS parallel benchmarks separately, and executed on the Tianhe-1A supercomputer. In view of the test comes about, the creator dissected the execution of MPI+OpenMP+CUDA and MPI+CUDA in various circumstances, and gave a proposal that developers ought to pick an appropriate programming design as per their own exploratory conditions in request to expand the computing ability of elite framework.

• III.    Proposed Performance Driven Frame Work

As per the previous section, the main drawback of the MPI and CUDA programming design is that the computational capability of CPUs within each compute node is not efficiently used. In order to address this issue, in this section, we explained about proposed hybrid programming model framework with the OpenMP model to exploit the hardware parallelism of multicore CPUs.

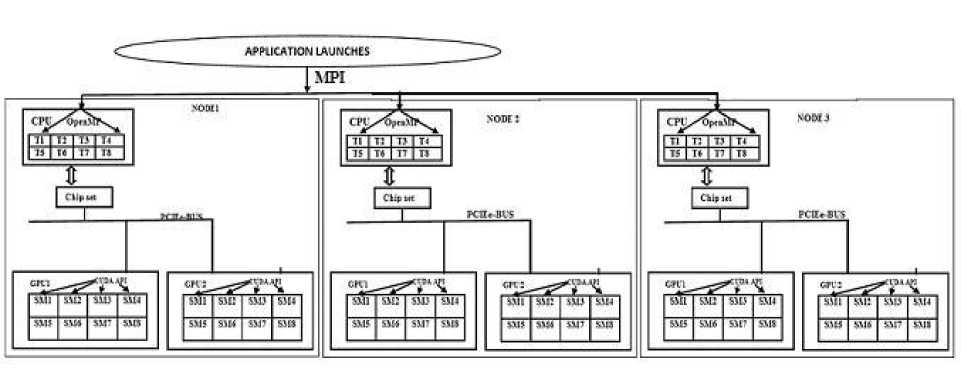
Fig.1. Performance driven frame work of homogeneous CPU and GPU cluster

Fig.1, shows proposed novel performance driven framework of heterogeneous architecture, where each node consists of one CPU and two GPU. The CPU and GPU communicate via PCI-E bus. Both CPU and GPU have their own storage. Each CPU has many cores. Each core has its own cache. The GPU has several Streaming Multiprocessors (SMs). The CPU is responsible for applications control, distributing tasks between CPU and GPU, originating the GPU computation and reading the result of the GPU.

In this framework, MPI is used to control the HPC application and to implement the communication processes between computing nodes in a heterogeneous cluster, by calling library routines to send and receive messages. MPI also controls the workload distribution and process synchronization, while OpenMP offers the ability to appropriately parallelize programs by introducing compiler directives and invoking subroutine calls [12]. All OpenMP programs follow the fork-and-join performance model and use the work-sharing directives to dispense the workload among the threads. OpenMP has the drawback of insufficient scalability due to the internal thread management overhead and the restricted CPU cores within the system. OpenMP is usually employed to explore the parallelism within each compute node of complex clusters built with multi core processors [16] whereas CUDA is used to compute the huge complex tasks on the GPU.

In this work, we have considered only one MPI process to handle the part of the work on each node. Each MPI process is used to control and communicate with the GPU. Due to this, we eliminate the underutilization of the device memory. On the other hand, compared with multiple MPI process per node, much fewer data transfers are performed by the proposed method which improves the memory-bandwidth. The MPI process spawns as many OpenMP threads as the amount of CPU cores within each compute node [6]. Only the master thread cooperates with GPU and the others perform relevant arithmetic operations in parallel. In general, a MPI process initially transfers the input data from CPU to GPU through the PCI-E bus [8]. Then, it invokes the CUDA kernel, in which all the GPU threads run the kernel in parallel. Lastly, the MPI process transfers the output data from GPU to CPU and thus improves the productivity and performance of the HPC Applications.

• A.    Hybrid Programming Approach

In this framework, we focus on building a strategy to cluster with the resources of many core CPU and multi core GPU. GPU is usually regarded as a data-parallel multi core system. Compute Unified Device Architecture (CUDA) is a registered framework from NVIDIA to develop applications on GPU [11]. The computational elements of algorithms written with CUDA are known as kernels, which, consist of many threads to execute the tasks in parallel. GPUs can only read/write from memory attached to the host. The GPU acquires a block of main memory with CUDA interfaces, such as cudaMallocHost(). Before GPU kernel starts executing, data must be moved from main memory into the device memory; and after the execution, results need to be moved back to the memory. This is done using cudaMemcpy().

There are numerous reasons to combine three parallel programming approaches of MPI, OpenMP, and CUDA on a heterogeneous cluster [13]. A common reason is to enable solving problems with a large data size to fit into the memory of a single GPU, or that would require an unreasonably long compute time on a single node. Another factor is to exploit the performance improvement, by making use of the CPU as a part of computation. To use the CPU as a part of computation, we utilize another parallel programming model known as OpenMP. Again to exploit the power of distributed architecture we are making use of MPI programming model. Due to above said observations we are combining MPI+OpenMP+CUDA on heterogeneous CPU-GPU architecture.

• B.    Workload Division Strategy

This section describes a workload distribution strategy in which the workload is assigned to each node on a hybrid CPU/GPU cluster [10]. Distribution of the work load between CPUs and GPUs is done based upon their computation capacity. If we assign too little work to the

CPU, it is not enough to keep the CPU busy during GPU kernel launch and memory transfer, and thus the latency cannot be well hidden. On the other hand, if we assign too much work to the CPU then, the GPU kernel has to wait for the CPU to finish the tasks before generating the result. In this work we are addressing the question, what is the optimal CPU and GPU workload for each core under different parallel configurations? We plan to consider asymmetric work load division, which requires division ratio. This is proportional to compute speed and hardware specification of the CPU and GPU. To predict work load ratio, we are considering multiple factors such as problem size, node counts, hardware configurations, computational speed, and communication rate of each node. By using these parameters in our proposed framework, our strategies decide optimal workload for the CPU and GPU depending on their computational capacity.

Let W be the size of total workload per cluster, n be the number of nodes on CPU-GPU heterogeneous cluster. Load per node is represented by L node , memory bandwidth of CPU and GPU represented by C_pbw, G_pbw , Speed of CPU processor and GPU processor by S_CP and S_GP, j is represented as specific CPU, C is represented as cores, N C represents number of cores. In the beginning when assign the full HPC application workload W to the cluster need to compute the load for individual nodes [ L nodei ] by considering multiple factors such as problem size(W), node counts[i=1 to n], hardware configurations i.e number of CPU cores [ N_c pi ] and Number of GPU cores [N Gpi ], computational speeds of processors[ S CP i and S GP i ], computing capability [ C_no dei =Z * S j where C node i represents computing capability and S j represents calculation intensity of task j] of each node in a cluster communication rate and kernel memory bound at each node we balance the load according to the realistic memory bandwidth values [ C pbwi , G pbwi ]. A good CPU+GPU execution must take the different computational speeds into interpretation. Failing to do so will normally lead to a severe load imbalance since the fast GPU will continuously wait for the slow CPU to complete its workload, and thus to poor performanc e.

Lnodei =

w

5P-₁(GCPi,SGPi,Cpbwi,Gpbwi ,NCpi,NGpi,Cnodei)

After computing varying workload to individual nodes, then on each nodes of a cluster a fraction of the workload is dynamically distributed among CPU cores and GPUs based on their performance capabilities.

Let T[Cpi+Gpi] execution time of the HPC applications on the CPU+GPU and T Gpi execution time of the HPC applications on the GPU and P[Cpi+Gpi] performance(GFLOPs) presented for target HPC applications on the CPU+GPU and P Gpi performance(GFLOPs)presented for target HPC applications on individual nodes in a cluster are computed using eq(5). Hence, the load on the CPU [ L_CPi ] is computed using eq(2).

Lcpi = [Lnodei * (1 - (—— ^^-))] (2) ' I V PGpi+P(Gpi+Cpi)/ ^v '

After dynamically computing fraction of load on the CPU, Now the load per core on each CPU of the respective nodes in a cluster L CPi /C j is computed using eq(3). Here, we divide the fraction of the load is among numerous available cores N C on CPU.

l.CPi

^L C ^pi /Cj = —

Now load on GPUs is obtained L GPi by using eq (4). After determining the fraction of the workload ratio to the CPU, and assign the remaining work load to the available number of GPUs in the respective nodes in a cluster.

LGPi = (Lnodei - LCPi)            (4)

By using the above eq(2), eq(3) and eq(4), we compute GPU workload and CPU workload. Workload can potentially be distributed properly to the computation resources of a heterogeneous system, and therefore achieve better performance with suitable work load division between CPU and GPU. Our CPU+GPU programming approach (MPI+OpenMP+CUDA) is able to utilize the different processing units and maximize overall FLOPS (Floating point operations per second).

• C.    Performance Evaluation

The overall goal of homogeneous implementation is to utilize the computational resources efficiently to achieve peak applications performance. The implementation of HPC applications on the proposed framework of heterogeneous CPU+GPU cluster  using hybrid programming model(MPI+OpenMP+CUDA) should perform better when compared to that of GPU (CUDA). In this work, we are comparing applications performance by measuring execution time and GFLOPs. The GFLOPs is computed using the eq (5).

gflops = [- ^ ^op— ] * 1.0e ^-9         (5)

L Execu.tion_timeA

Where,

N op is Number of operations

Execution _Time= (ElapsedTime *1.0e-3)

ElapsedTime=(Process_end_time)-(process_start_time)

• D.    Hybrid Implementation of Dynamic Computation of N Random numbers

The random numbers are intended to produce a sequence of numbers which appear at random. There are different types of random numbers. They are custom random numbers, pseudo random numbers and dynamic random numbers. Custom random numbers function displays the numbers within the specified upper and lower limit, but for dynamic random numbers there are no upper and lower range limits. Some of the applications of dynamic random numbers are modern electronic casino game and electronic noise studies in physics. Another application of the random number is in the field of operational research. In this application, random numbers are used to provide optimal or near optimal solution to decision making problems.

Once the application is deployed to the CPU, user need to provide the maximum limit. Depending upon the number of CPU cores, OpenMP threads will be established for each core. Then each thread, creates two sets of threads. The first set of threads is responsible for generating N Dynamic Random numbers vectors and controlling the GPU of the same node in the cluster. In the first set of threads, once some of the threads transfer the data to the GPU memory CUDA kernels compute N dynamic random numbers vector additions. While other threads in a set of threads perform the generation of N dynamic random vectors on CPU concurrently. The threads in the second set are busy with computing N random vector numbers. This approach holds the extra benefit of thread synchronization, in that one thread set will not disturb the threads in the other set. In this application, some threads in the host generate the N dynamic random numbers using OpenMP. Others OpenMP threads are busy in controlling GPUs and to transfers generated random numbers from host memory to device memory for computation. Using CUDA, it does the computation in device memory and sends the computation results to host memory MPI is used to transfer data to other nodes in a cluster. Hence by running the applications on homogeneous platform, we are in a position to utilize the compute resources efficiently.

• E.    Hybrid Implementation of Pinned and pageable data transfer for SAXPY application

Inter-process communication is a process of exchanging data among numerous computing devices with specific procedures by means of communication protocols. Single-Precision A•X plus Y (SAXPY) is one of the benchmark applications in HPC. It is a function in the standard Basic Linear Algebra Subroutines library. SAXPY is a combination of scalar multiplication and vector addition. It takes two input vectors of floating point values for X and Y with N elements each, and a scalar value A. It multiplies each element X by A and adds the result to Y.

Z=A*X+Y

Here X, Y and Z are vector and A are a scalar value. By utilizing a MPI process, will communicate with other nodes in a cluster pinned and pagable data transfer technique, we compute the GFLOPs of the application respectively. The memory of the host is pageable default. When the Device wants to access the Host memory it directly cannot access in pageable data transfer. Hence, a separate memory is used to store the host memory to access from the device. This memory is called as pageable memory. For data transfer, a separate memory is utilized to store data temporarily which consumes extra memory. To avoid this, a pinned data transfer technique is utilized. In pinned data transfer, there is no requirement for temporary memory storage in the host. If a device wishes to access the data from the Host, it directly accesses from the Pinned memory. Hence it avoids the momentary storage of memory. Using this pinned memory technique. We are computing the GFLOPS with different data size using eq(5).

To overlap computations and communications with the intra-node data exchanges, we adopted a hybrid programming model that involves MPI, OpenMP and CUDA. In such a methodology, task parallelism is important. Some of the OpenMP threads are committed to the part of the computation i.e generation of vector X and vector Y, while the remaining OpenMP threads handle other tasks, such as data movement between the CPU and GPU in a node. MPI process will communicate with other nodes in a cluster. While CUDA is used to make computation i.e it multiplies each element vectors X by A and adds the result to vector Y and intra-node communication, Subsequent CPU-GPU data conversations are implemented via cudaMemcpyAsync. By applying pinned memory technique, we overcome the overhead of data transfer between the CPU and GPU in our hybrid programming model approach (MPI+OpenMP+CUDA) on hybrid CPU+GPU cluster.

• IV.    Experiments and Results

• A.    Experimental setup

Experiments were conducted validating the proposed hybrid framework in terms of GFLOPs of the benchmark applications. We conducted experiments on in-house cluster, which is under our administrative control. The experiments were conducted on eight heterogeneous nodes.

• 1 .Three nodes with Six-core/socket Intel(Xeon(R) E5-2620 CPUs, GPU (NVIDIA Tesla M2075) with 32GB RAM which is expandable up to 500GB with 447 cores.

• 2 . Five nodes with Six-core/socket Inter Xeon CPU processor at 2.40 GHzx of 31GB RAM with two GPUs (NVIDIA Quadro K2000) configuration include the system type that is Dell precision R5500 with 227 cores.

Each node is configured with MPICH2-1.2 MPI library to make communication between nodes in a cluster. The compilers used are GCC version 4.4.7 and NVIDIA nvcc version 5.0.

We have tested our homogeneous framework for two different benchmark applications i.e Dynamic computation of N random numbers vector addition and saxpy applications. The application parameters for Dynamic computation of N random numbers vector addition are two input vectors of N size random numbers and for saxpy applications two input vectors of N size of elements each. For each input size, we will consider the average performance in GFLOPs.

• B.    Results of Dynamic Computation of N Random numbers:

In these HPC applications, once the application is launched to the cluster, total workload is divided among the nodes in a cluster. By using eq(1) load per node is computed and assigned to the individual nodes in a cluster. In each node of a cluster workload is dynamically distributed among CPU and GPUs based on their computing capabilities. By using eq(2) and eq(3) part of the total assigned load to node(Lnode) is assigned to the CPU and it’s cores and remaining workload is computed by using eq(4) and assigned to the GPUs. In these HPC applications, we will generate two vectors of N dynamic random numbers and compute the vector additions. Here, instead of deploying full computation to GPU. We assigned small portion of workload i.e to generate the N dynamic random numbers to CPU. CPU uses parallel programming model OpenMP to generate the N dynamic random numbers. Then, MPI is to communication between the nodes in a cluster. Then by using CUDA, concurrently compute the N dynamic random numbers vector addition to device memory and sends the computations results to host memory.

Table.1, list the size of dynamic random numbers and performance of N dynamic random number vector addition computation in GFLOPs using our hybrid programming model [MPI+OpenMP+CUDA] and compared against Simplice Donfack Hybrid programming model and using three nodes of a cluster each has one GPU( NVIDIA Tesla M2075) and one CPU of Intel(Xeon(R) E5-2620.

Table 1. Test Results of N Dynamic Random Numbers vector addition for three TESLA Nodes in cluster

Sizes of Random Numbers	GFLOPs on Simplice Donfack Hybrid programming model	GFLOPs on Hybrid Programming Model	% of Performance Improvement against Simplice Donfack Hybrid Programming Model
100000	6.9015E-05	0.002813731	97.54720627
200000	8.76824E-05	0.001461027	93.99857955
400000	9.87596E-05	0.000526759	81.25148139
600000	0.000102807	0.000556168	81.51507155
800000	0.000122579	0.00026578	53.87947414
1000000	0.000125694	0.00024264	48.19742478

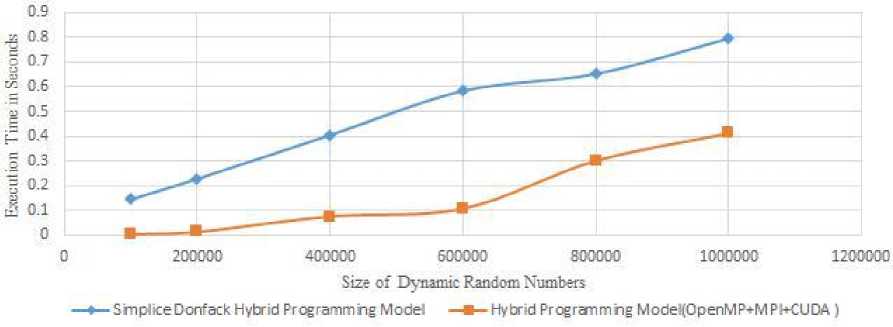
Fig.2. Execution time of dynamic N random number vector addition for three TESLA nodes in a cluster

• Fig.2, shows execution time of Simplice Donfack Hybrid programming model and our hybrid parallel programming model[MPI+OpenMP+CUDA], for different problem sizes of dynamic N random numbers addition computation. In the figure, X-axis shows size of the dynamic random numbers and Y-axis shows the Execution time in seconds. As the random number size increases the execution time of the hybrid programming

model is also increases because during the initial stage of experimental small chunk of the load is shared among more number of CPU-GPU cores, then it takes less time. But as the load increases it takes more number of CPU-GPU cores and data transmission between CPU-GPU leads increase in execution time. But as our proposed hybrid model gives better execution time over Simplice Donfack hybrid programming model.

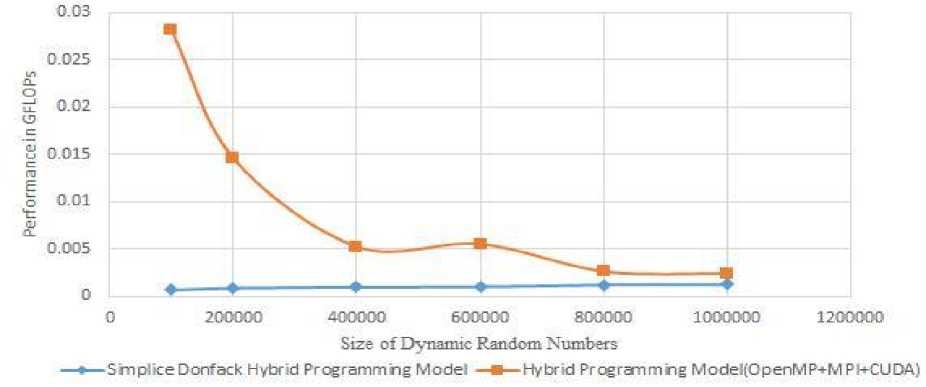
Fig.3. Performance results of dynamic N random number for vector addition three TESLA nodes in a cluster

After computation of execution time, we computed the GFLOPs using eq(5). Fig.3, plots the performance improvement in hybrid programming model for different problem sizes of dynamic N random numbers vector addition computation over Simplice Donfack Hybrid programming model. In the figure, X-axis shows size of the dynamic random numbers and Y-axis shows the performance in GFLOPs. We find that during the initial experiment, the percentage of performance improvement is high. For smaller problem size such as 100000 we are able to achieve 97.54% over Simplice Donfack Hybrid programming model. In later stage percentage of performance improvement is low i.e for 1000000 random numbers 48.19% performance improvement. As dynamic random numbers size increases, the percentage of performance (in floating point operations per seconds)

improvement in hybrid programming model will decrease because of CPU-GPU data transmission (communication) time that prevents GPU to exploit it’s parallel computing capacity completely. But the proposed hybrid programming model gives better performance i.e for varying problem sizes, we have achieved on an average performance improvement of 76.06% comparatively with Simplice Donfack Hybrid programming model.

Table.2, lists sizes of N dynamic random numbers and performance of N dynamic random numbers vector addition computations in GFLOPs using our hybrid programming model[MPI+OpenMP+CUDA]. And compared against simplice donfack hybrid programming model with five node each has two GPUs (NVIDIA Quadro K2000) and one CPU of Intel(Xeon(R) E5-2620 on each node of a cluster.

Table 2. Test Results of N Dynamic Random Numbers vector addition for Five nodes each with two GPUs(Quadro K2000) in a cluster

% of Performance Improvement

	GFLOPs on	GFLOPs on	against Simplice Donfack
Sizes of Dynamic Random Numbers	Simplice Donfack Hybrid programming model	Hybrid Programming Model	Hybrid Programming Model
100000	5.91856E-05	0.000877886	93.25816761
200000	7.75627E-05	0.002308403	96.63998511
400000	9.01941E-05	0.002174386	95.85197345
600000	9.29875E-05	0.001165230	92.01981254
800000	9.96532E-05	0.000533853	81.33321043
1000000	9.66594E-05	0.000177678	45.59851531

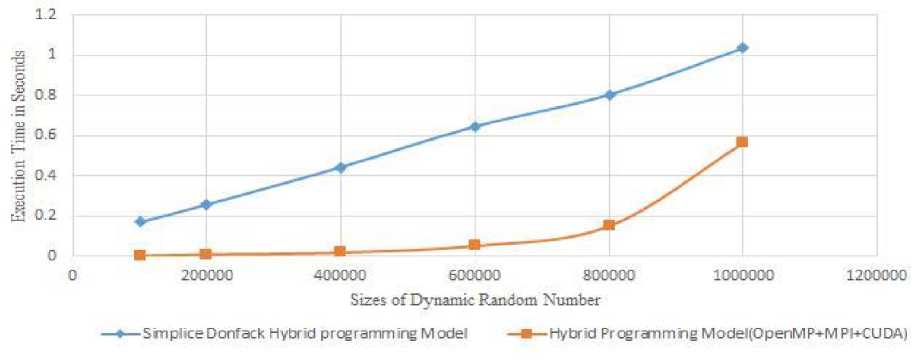
Fig.4. Execution time of Dynamic N Random number vector addition for five nodes with each has two GPUs(QUADRO) on each nodes in a cluster

Fig.4, demonstrates execution time of Simplice Donfack Hybrid programming model and our hybrid parallel programming model[MPI+OpenMP+CUDA], for various data input sizes of dynamic N random numbers vector addition computation. In the figure, X-axis shows size of the dynamic random numbers and Y-axis shows the execution time in seconds. As the random number sizes increase the execution time of a hybrid programming model also increases because during the initial stage of experimental small chunk of a load is shared among more number of CPU-GPU cores, then it takes less time. But as the load is raised takes more number of CPU-GPU cores and data transmission between CPU-GPU leads increase in execution time. But our proposed hybrid model gives better execution time over simplice donfack hybrid programming model

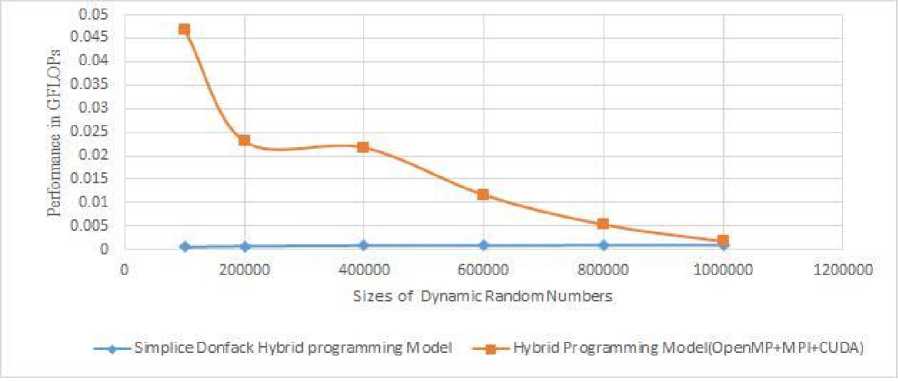
Fig. 5. Performance results of Dynamic N Random number vector addition for Five nodes with each has two GPUs(QUADRO) on each nodes in a cluster.

After calculation of execution time, we processed the GFLOPs utilizing eq (5). Fig.5, plots the percentage of performance improvement in our hybrid programming model for varying problem sizes of dynamic random numbers vectors addition computation, over simplice donfack hybrid programming model. In the figure, X-axis shows sizes of the dynamic random numbers and Y-axis shows the performance in GFLOPs. We find that during the initial experiment, the percentage of performance improvement is high. For smaller problem sizes such as 100000 we are able to achieve 93.25% over Simplice Donfack Hybrid programming model. In later stage percentage of performance improvement is low i.e for 1000000 random numbers 45.59% performance improvement is achieved. As dynamic random numbers size increases, the percentage of performance (in floating point operations per seconds) improvement in our hybrid programming model will decrease because of CPU-GPU data transmission(communication) time that prevents GPU in exploiting it’s parallel computing capacity completely. But still proposed hybrid programming model for different problem sizes we have achieved on an average improvement of 84.11%. Performance comparatively with simplice donfack hybrid programming model.

• C.    Results Pinned and pageable data transfer for SAXPY applications.

In this application, using OpenMP generate the two vectors X and Y then with CUDA multiplies each element vectors X by A and adds the result to vector Y it happens concurrently with OpenMP, for Pinned and pageable data transfer technique by varying different size(Gb) of input data. Table. 3, lists size of data transfer rate for pageable and pinned memory on three nodes of cluster where each node has NVIDIA Tesla M2075 for hybrid programming model.

Table 3. Test results of performance of saxpy on hybrid programming model on tesla node

Sizes of Data transfer in Gb	GFLOPs in Pagable Technique	GFLOPs in Pinned Technique	% of Performance Improvement in Hybrid Programming Model
0.03125	1.27438E-11	2.20574E-11	42.22444278
0.06250	1.96079E-11	3.21419E-11	38.99583633
0.12500	3.23627E-11	5.1427E-11	37.07050331
0.25000	5.4256E-11	8.49039E-11	36.09720068
0.50000	7.23413E-11	8.49039E-11	14.79626757

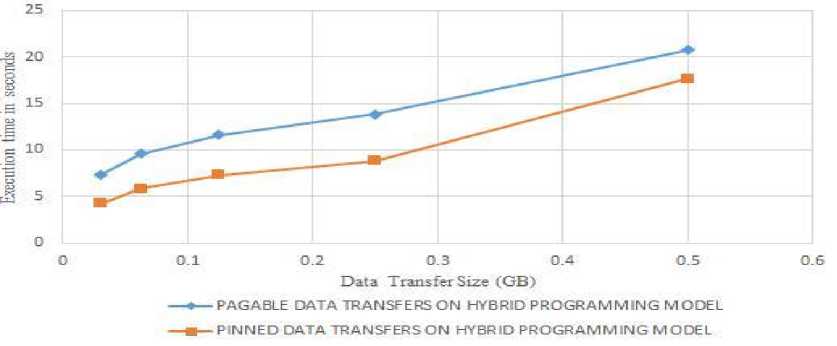
Fig.6. Execution time of saxpy on hybrid programming model varying data transfer for TESLA Node

Fig.6, shows the execution time of pagable and pinned memory technique for saxpy applications on hybrid programming model for varying data transfer size(Gb) on TESLA 2075 based cluster. The X-axis indicates size of data transfer in Gb and Y-axis indicates execution time in seconds. In the graph, we can no-tice that pinned memory technique take less execution time when compared with pagable memory technique.

After computation of execution time, we computed performance of saxpy in GFLOPs using eq(5). The Fig.7, plots comparison of pageable and pinned memory for saxpy applications on a hybrid programming model. Where the X-axis indicates size of data transfer in Gb and Y-axis indicates performance in GFLOPs. Using pinned memory technique, different problem sizes we have achieved an average improvement of 33.83% during the initial experiment, the percentage of performance improvement is high. For smaller problem size such as 0.03125Gb.

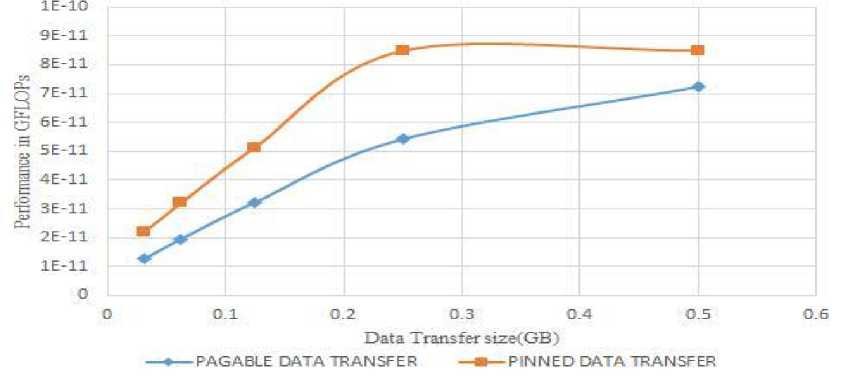
Fig.7. Performance saxpy in hybrid programming model varying data transfer for TESLA Node

We are able to achieve 42.22% over pagable memory technique. In later stage percentage of performance improvement is low i.e for 0.5Gb data transfer 14.79% performance improvement. As data input size increases, percentage of performance (Floating point operations per seconds) of data transfer rate decreases.

Table. 4, list size of data transfer rate in Gb for pageable and pinned memory on five nodes, each has two

GPUs (QUADRO K2000) in each nodes of a cluster using hybrid programming Model. MPI is used to make communication between nodes in a cluster. Where some of threads of OpenMP are used in computation and others are in controlling GPU. CUDA multiplies each element vectors X by A and adds the result to vector Y happens concurrently with OpenMP.

Table 4. Test results of performance of saxpy in hybrid programming model on QUADRO based cluster

Sizes of Data Transfers in Gb	GFLOPs in Pagable Technique	GFLOPs in Pinned Technique	% of Performance Improvement in Hybrid Programming Model
0.03125	1.52334E-11	2.97221E-11	48.74716150
0.06250	2.0502E-11	3.13249E-11	34.55056131
0.12500	3.65677E-11	6.01359E-11	39.19157683
0.25000	4.85294E-11	8.12054E-11	40.23868186
0.50000	8.21209E-11	1.21305E-10	32.30230863

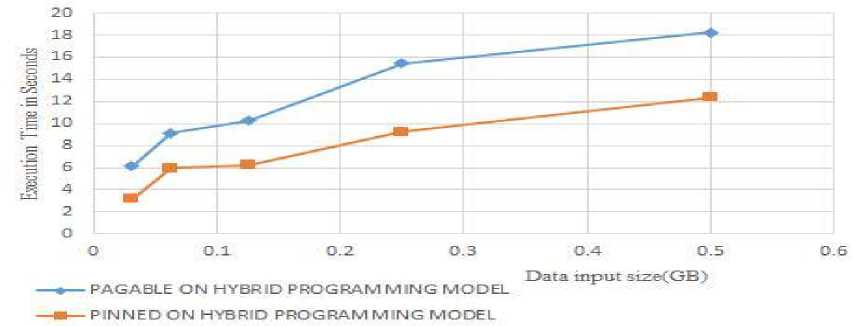
Fig.8. Execution time of saxpy on hybrid programming model for varying data transfer for QUADRO Node

The Fig.8, shows the execution time of pagable and pinned memory technique for saxpy applications on a hybrid programming model for varying data traffic size in Gb. The X-axis indicates size of data transfer in Gb and Y-axis indicates execution time in seconds. In the graph, we can notice that pinned memory technique take less execution time when compared with pagable memory technique.

After computation of execution time, we computed performance of saxpy in GFLOPs using eq(5). Fig.9, plots comparisons of pageable and pinned memory for saxpy applications on a hybrid programming model. Where the X-axis indicates size of data transfer in Gb and Y-axis indicates performance in GFLOPs. Using pinned memory technique, for different problem size we have achieved on an average improvement of 39.00%. We have determined that during the initial experiment.

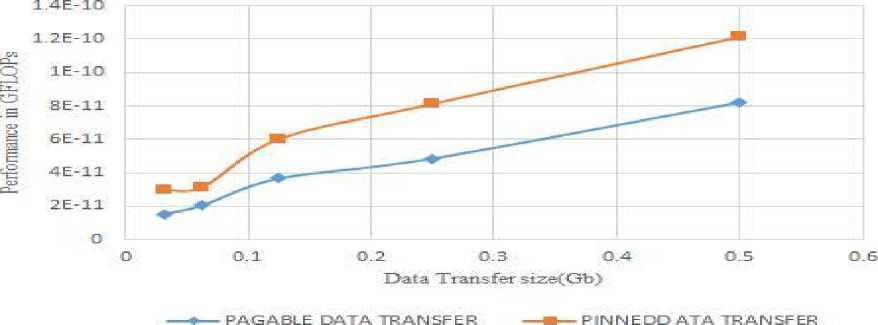
Fig.9. Performance result saxpy on hybrid programming model for varying data transfer for QUADRO Node

The percentage of performance improvement is high. For smaller problem size such as 0.03125Gb, we are able to achieve 48.74% over pagable memory technique. In later stages percentage of performance improvement is low i.e for 0.5Gb data trans-fer 32.30% performance improvement is achieved. As data input size increases the percentage of performance (oating point operations per seconds) of data transfer rate also decreases.

• V.    Conclusion

In order to effectively emprise the computational capability of heterogeneous HPC systems, must utilize the appropriate hybrid programming pattern [MPI+OpenMP+CUDA] is practically suitable to accelerate the HPC applications to define essential parallelism characteristics compared to Simplice Donfack Hybrid programming model. In this work, we have constructed    a hybrid    computing platform

[MPI+OpenMP+CUDA] for hybrid CPU+GPU clusters and introduced analytical workload division strategy to distribute the potion workload dynamically between CPU and GPUs according to their relative computational capacities within eight compute nodes cluster. And by launching one MPI process to each compute nodes in a cluster. We have described our experience by implementation of two benchmark HPC applications namely N dynamic vector addition and saxpy. Later we compared our framework with hybrid platform [MPI+OpenMP+CUDA] against Simplice Donfack Hybrid programming model. After exhaustive study of experimental results, we have obtained the observations such as, utilizing hybrid programming model boosts the performance (GFLOPs) than that of conventional programming model. We have observed that using a hybrid programming model an average performance improvement of 76.06% and 84.11% is observed on NVIDIA TESLA M2075 cluster and NVIDIA QUADROK 2000 cluster respectively for N dynamic vector addition when compared with Simplice Donfack Hybrid programming model. Also using pinned memory technique with hybrid computing model an average performance improvement of 33.83% and 39.00% on NVIDIA TESLA M2075 and NVIDIA QUADRO K 2000 clusters respectively is observed for saxpy applications when compared with pageable memory technique, because of its varying hardware configurations and cores.

As a future work, this work will be extended for more number of nodes in a cluster and optimizing the workload division among CPUs-GPUs heterogeneous architecture in order to utilize resources efficiently to improve the performance of HPC applications.