Периодические орбиты одного класса релейных свободных осцилляторов

Системы автоматического управления, содержащие релейный гистерезис в контуре обратной связи, известны давно и широко используются в настоящее время [8], [9]. Они исследовались как приближенными, так и аналитическими методами, но до сих пор многие вопросы динамики таких систем далеки от своего решения. В частности, не решен вопрос о разбиении пространства параметров этих систем на области различного динамического поведения. Продвижению в направлении решения этого вопроса аналитическими методами и посвящена данная работа.

Рассмотрим систему автоматического управления

X = AX + Bu ,             (1)

где u = f ( a ), a = ( Г, Х), X e E n , постоянные векторы В, Г е E n ; A - ( пхп ) - постоянная вещественная матрица; ( Г , Х ) – скалярное произведение векторов X и Г ( Г Ф 0); f ( a ) - нелинейная неоднозначная функция, характеризующая нелинейный элемент систем:

I m i при -«< ст <  £ 2 , f ( СТ ) = 5

^ m 2 при £ 1 < ст <+ю ,

где m 1 < 0 <  m 2 , £ 1 <  0 <  £ ₂ . Гистерезисная нелинейность релейного типа (2) вводится при математическом описании систем автоматического управления, если имеет место пространственное запаздывание управляющих механизмов. На плоскости ( f, σ ) гистерезисная петля обходится против часовой стрелки. Пусть все собственные числа матрицы A имеют отрицательные вещественные части (Re Xi < 0), ( Г, В ) Ф 0 и выполнены условия:

- ( Г , A ^-1 Bm 1 ) > £ 2 , - ( Г , A ^-1 Bm 2 ) < £ 1 .     (3)

Любая траектория системы (1), (2) состоит из кусков траекторий системы вида

X = AX + m i B ( i = 1, 2 ) .            (4)

В фазовом пространстве точки «сшивания» этих кусков принадлежат поверхностям переключения ( Г,X ) = £ i ( i = 1,2 ) , и, в частности, периодический режим может состоять из двух кусков траекторий в силу разных систем (4) (так называемая унимодальная периодическая орбита).

ОКРЕСТНОСТЬ ПЕРИОДИЧЕСКОЙ ОРБИТЫ

Обозначим M орбиту периодического режима в фазовом пространстве.

Решение системы (1), (2) – вектор-функ-ция Xtt , X 0 , m i ), заданная и непрерывная при t >  0, X (0, X 0 , m i ) = X 0 . Если ( Г , X ₀ ) = £ _х, то эта вектор-функция удовлетворяет равенству X ₀ = X ( ω , X ₀, m_i ), где X 0 е M , го - период решения соответствующего M , ω = t ₁ + t ₂ ( t ₁ – время, соответствующее движению от одной гиперплоскости переключения до другой в силу (4) при i = 1, а t ₂ – время при i = 2). Функция X ( t , X ₀, m_i ) – дифференцируемая по t для всех t е (0, 1 1 ) и всех t е (t 1 ,1 1 + 1 2 ), поэтому в окрестности всей орбиты M невозможно рассматривать приведенную систему [1] системы (1), (2). Действительно, построим гиперплоскость P_t , проходящую через X ( t , X ₀, m_i ) при фиксированном t и определяемую уравнением

( X - X ( t , X 0 , m , .) , X ( t , X 0 , m , .)) = 0 ,       (5)

где Х e E n . Гиперплоскость является нормальной гиперплоскостью к кривой, определяемой X ( t , X ₀, m_i ), при данном фиксированном t . На P_t можно ввести систему координат, выбрав в качестве ее начала точку X ( t , X ₀, m_i ), а в качестве единичных ортов осей – попарно ортогональные и непрерывно дифференцируемые

векторы. Таким образом, переходим к исследованию окрестности траектории методами теории устойчивости [2]. В силу условий, наложенных на матрицу A , можно утверждать, что любая траектория X ( t , X ₀, m_i ) в силу системы (4) является асимптотически орбитально устойчивой. Именно из кусков этих траекторий составлена периодическая орбита M . Обозначим эти куски M ( X ₀, m ₁) и M ( X 0 , m 2 ). Обозначим p ( X , M ) = inf || X - Y , S ( M , s) = { X : X e E n , p ( X , M ) <  s }, S ( M, s) - s -окрестность траектории, ε > 0. Очевидно, что в точках переключения периодического режима воспользоваться изложенной методикой нельзя.

По аналогии с непрерывным случаем решение X ( t , X ₀, m_i ), которое соответствует орбите M , будем называть орбитально устойчивым, если для произвольного ε > 0 существует такое 5 = 5 ( s ) > 0, что для любого X e S ( M ( X ₀, m i ) , 5 ) при t >  0 будем иметь X ( t, X, m^ e S ( M ( X ₀, m J , e ) .

Обозначим через X ₀ ¹ и X ₀ ² точки переключения периодического режима и ( Г , X 0 ) = £ 1 , ( Г , X 0 ) = I 2 . Ясно, что строить гиперплоскости P_t для исследования окрестности можно до тех пор, пока множество S_p = S ( M ( X 0 , m i ), 5 ) n P_t имеет не более одной общей точки с ( Г, X ) = £ i . Обозначим S р множество, имеющее одну общую точку с ( Г, X ) = £ i . При этом можно считать, в силу вида системы (1), (2), что между S р и соответствующей гиперплоскостью ( Г , X ) = £ i точки, принадлежащие периодическому режиму, могут быть представлены так:

X = Xj +t(AX^ miB) + о(|t|), j = 1, 2, где t принадлежит некоторой достаточно малой окрестности точки t = 0. Тогда, если выполняются в точках переключения следующие неравенства:

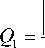
Г ( AX ₀ ² + m 1 B )| | Г^Т ( AX ₀ ² + m 2 B ) ||Г||||АХ 02 + m i B|| " ||r||||AX 02 + m 2 b||

I Г^т ( AX 0 + m 2 B )|  | r^T ( AX 0 + m 1 B )|

N ¹ = || r||||AX 0 + m 2 B|| " ||r|||AX 0 + m 1 B|| " N 2

то периодический режим (или, иначе, орбита M ) соответствует орбитально устойчивому решению системы (1), (2).

Условия (6) имеют прозрачный геометрический смысл, но в общем случае могут и не выполняться.

Пусть неравенства (6) не выполняются. Воспользуемся тем, что в окрестностях типа S(M(X0, mi), δ) вдоль траекторий M(X0, m1) и M(X0, m2) имеет место сжатие в плоскостях типа Pt. Обозначим в равенстве (5) Z = X – X(t, X0, mi). Рассмотрим матричное уравнение ATV + VA = –W, где V и W – постоянные симметрические матрицы, при этом V(Z) = ZTVZ и W(Z) = –ZTWZ – соответственно положительно определенная и отрицательно определенная формы.

Обозначим a = min 2 ^( V ) , a , = max 2 ^( V ) и b = min 2 k ( W ) , b , = max 2 k ( W ) , тогда в силу условий, наложенных на A , имеем 0 <  a <  a ₁, 0 <  b <  b ₁. Используя неравенство (6) и свойство экспоненциального сжатия вдоль траекторий, получаем, что для орбитальной устойчивости периодической траектории M должно выполняться неравенство

IIZoil > aO-e-“™N, N2 Q, Q2I|Z0 , где а = b2 (a,) 1, Z0 - начальный вектор в некоторой нормальной гиперплоскости, содержащей множество вида S'р, то есть Z0 лежит в этом множестве. Таким образом, должно выполняться неравенство:

а 1 a -¹ e "“^m N , N 2 Q 1 Q 2 <  1. (7)

Предложение 1. Если у системы (1), (2) все собственные числа матрицы A имеют отрицательные вещественные части, ( Г, В ) ^ 0 и выполняются неравенства (3), (6) или (3), (7), то периодический режим с двумя точками переключения является орбитально устойчивым периодическим решением системы (1), (2).

Отметим, что числа a , a ₁, b , b ₁ находятся не однозначно и зависят, например, от выбора матрицы W . Кроме того, как правило, легче проверить выполнение неравенства (6) в некоторых множествах, содержащих точки переключения и непрерывно отображаемых в себя в силу решения системы (1), (2). Взяв в одном из этих множеств начальное приближение точки переключения, можно получить в силу системы (1), (2) итерационный процесс, сходящийся к этой точке. Поэтому надо проверять неравенства (6) в некоторых окрестностях точек X ₀ ¹ и X ₀ ² . Из приведенных рассуждений следует, что мы рассматриваем изолированную периодическую траекторию, в окрестностях точек переключения которой траектории системы (4) не касаются, по крайней мере, одновременно гиперплоскостей переключения ( Г , X ) = £ i ( i = 1, 2 ) .

ИЗОЛИРОВАННОСТЬ ПЕРИОДИЧЕСКИХ ОРБИТ

Обсудим условия изолированности орбит и свойство трансверсальности, то есть когда траектории системы, например вида (4), не касаются гиперплоскостей переключения. Условия касания траекториями поверхностей переключения: Г^Т ( AX + m_iB ) = 0, i = 1, 2, откуда получаем:

Г^ТAX = – Г^Тm_iB , i = 1, 2. (8)

Уравнение (8) – это уравнение гиперплоскости. Если Г Т В Ф 0, то в точках X на

( Г, X ) = I i ( i = 1,2 ) нет одновременного касания в силу обеих систем (4), если m 1 Ф m 2 . Таким образом, получаем уравнения прямых, лежащих на ( Г , X ) = £ i ( i = 1,2 ) и таких, что в точках этих прямых выполняется условие (8), то есть:

/ Г^ТХ = £ ,   ( j = 1,2 ) ,

Г^ТАХ = - F^TBm_i  ( i = 1,2 ) , Г^ТВ Ф 0.

Следовательно, точки переключения орбиты не должны принадлежать прямым (9) – это условие трансверсальности для системы (1), (2).

С геометрической точки зрения не должны касаться поверхностей переключения траектории в силу уравнения (4), приходящие в окрестность точки переключения орбиты M , так как если в этом случае уходящие из окрестности траектории касаются, то при переходе через точку переключения имеет место сжатие по отношению к изучаемой траектории M . Если наоборот, то имеет место удаление от изучаемой траектории M при рассмотрении изображающих точек в нормальных плоскостях P_t . Это поясняет смысл неравенства (6).

Отметим, что условия (9) легко проверить, если знаем, хотя бы приближенно, координаты точек переключения M .

Условия изолированности орбиты тесно связаны с проблемой существования периодического решения системы (1) не только с функцией вида (2), но и с более сложными неоднозначными функциями f ( σ ).

Периодические стационарные колебания можно построить, если найти все периодические решения интегрального уравнения

• <7(0 = Г^те^л' (5 -е^Лш У j e^^Bf (<т( г))с/г +

+ Гт J^4*' Г^В/(сг(г))<7г, где ω – период искомого периодического решения. Из уравнения (10) следует находить функцию σ(t) и ее период ω. В (10) функция f(σ(t)) имеет кусочно-постоянные значения, зависящие от положения текущей координаты X(t) в En. Матрица (E – eAω) должна быть неособой, то есть среди собственных чисел матрицы A нет чисто мнимых вида pi, где p = 0, ±1, ±2, .„, тогда уравнение (6) имеет единственное решение [2]. В работе [9] утверждается, что для того, чтобы унимодальная периодическая орбита, то есть с двумя точками переключения, с полупериодом T0 была изолированной, необходимо и достаточно, чтобы (в обозначениях оригинала [9])

N(eAT - E)n N(Г) = {0}, (11) где N обозначает нуль-пространство соответствующей матрицы. Более того, существует континуум периодических орбит, когда (11) не выполняется. Этот результат появился посред- ством уточнения работы [5], из условия существования отображения плоскости в плоскость и условия, что неподвижные точки этого отображения являются изолированными. Множество N(Г) – это множество тех X, для которых ГTX = 0, то есть это уравнение гиперплоскости, переходящей через точку On, и аналогично множество N(eAT - E) - это множество тех X, для которых [eATo - E] X = O„.

Условие (11) выполняется, если уравнение [ e AT - E ] X = O_n имеет только тривиальное решение, а это происходит только тогда, когда rang [ e AT - E ] = n , то есть когда матрица [ e AT - E ] - неособая.

Следовательно, условие (11) не накладывает никаких новых условий на матрицу A по сравнению с ранее известными условиями. Кроме того, условие (11) получено лишь для симметричного случая гистерезиса при m 1 = -1, m 2 = 1, £ 1 = - 1 , £ ₂ = 1 . При этом известны достаточные условия сведения системы (1), (2) к симметричной системе [3].

Таким образом, для общего случая системы (1), (2) справедливо

Предложение 2. Если система (1), (2) имеет периодическую орбиту M с периодом ω и точки переключения этой орбиты не принадлежат множеству, определяемому условиями (9), матрица [ E - e A ™ J - неособая, то тогда периодическая орбита M является изолированной.

Пример. Рассмотрим систему вида (1), (2), где

- 1

А = - 10 - 1

0 ) 0 -1.

B =

Г 2 )

Г =

'- 2/3 ^ - 2/3

V— 4/3 > ч 2,

£1 = -1, m, = -1,

£ 2 = 1, m ₂ = 1.

При этом X 1 2 = -1 ± 10 i , X 3 = -1, то есть все Re λ_i < 0, и выпо ^, лняется условие (3). Эта система имеет две унимодальные периодические орбиты. Первая орбита – устойчивая с точками переключения

X0 =- X02 =( 0,1438 0,0059 0,6752) T, вторая орбита является неустойчивой с точками переключения

X 0 =- X ₀ ² = ( 0,6469 0,3651 0,2440 ) T .

Легко проверить, что второе равенство (9) не выполняется для этих точек. Обе орбиты являются изолированными.

Замечание. Сформулированные условия нисколько не уже условия изолированности (11), кроме того, Предложение 2 годится не только для унимодальных орбит, а вообще для кусочногладких орбит. Например, можно считать, что траектория имеет 2m точек переключения (m > 1 и точек конечное число) и в окрестности каждой из них имеет место свойство трансверсальности (9). При этом должно дополнительно выполняться условие: существует такое а е (0, 1), что при любом j (1 < j < n) max Re Л (Л) < -a < 0.

ОРБИТАЛЬНАЯ УСТОЙЧИВОСТЬ

Предположим, что нам удалось найти точки переключения периодической орбиты, то есть существует замкнутая траектория. Наша задача – исследовать эту траекторию на устойчивость. Каждая часть траектории в силу системы (4) может быть исследована с использованием нормальной плоскости P_t и уравнения Ляпунова, но этот подход не может быть использован в окрестностях точек переключения. Будем далее считать, что выполнены условия Предложения 2.

Пусть X ₀ – точка переключения, лежащая на плоскости ( Г , X ) = £ i , и пусть угол а 0 между векторами Г и AX ₀ – острый, то есть ( Г , AX ₀) > 0 и 0 < cos ^а о <  1, где cos _а 0 = j ^AX ^. ПреДположим, что матрица A такова, что для любого вектора C выполняется условие

.> ( AC , - C ) > II AC IIII C II

> cos

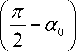
= sin a₀ .

Последнее условие перепишем так

( AC , — C)   .          ( Г , AX о )

----> Sin arccos 7^-777------77

ii ac iii c ii        L iini AX oil

Пусть для наглядности n = 3 и пусть точка X ₁ принадлежит произвольной траектории, плоскости P_t и одновременно поверхности переключения, тогда вектор ( X ₁ – X ₀) лежит в плоскости

(Г,X) = £ i. Построим систему ортов: г1 =

Пр AX

Г =       ⁰ , где Пр AX – проекция вектора

• 2 Пр AX0

AX0 на плоскость (Г,X) = ti, а орт Г3 выбирается так, чтобы он имел острый угол с вектором (X1 - X0). Построим матрицу V = £ Vk , где Vk=ГkГ kT. Обозначим X переменную точку исследуемой траектории между плоскостью Pt и точкой X0. Рассмотрим функцию г^Цх-ф^х-х^.

= АХТУАХ = ^^Т Ct АХ =(

А-=1^=1

Точка X1 рассматривается как «неподвижная», то есть X1 не зависит от t. Тог- да   V (X) = XT AT VAX + AXTVA AX.  Матрица

V ₁ = ГГ^T , поэтому

V ( X ) = X T A T V A X + A X T V 1 A A X <  0 ,   (13)

в силу того, что по условию трансверсальности (, V , Г ) > 0 , а ( Г, A X) >  0.

Выясним теперь знак V ₂ ( X ) , то есть покажем, что

V 2 ( X ) = X T A T V 2 X X + X X T V 2 AX =

= X T A T г 2 г T a x + a X T г₂ г T ax <  o.

Рассмотрим взаимное расположение векторов, входящих в выражение (14). Знак ( Г 2 , A X ) может быть любым, то есть ( Г 2 , A X ) <  0 или ( Г 2 , A X ) <  0. Выполняется условие AX ^ AX 0 при X ^ X ₀, обозначаем α ( t ) угол между вектором ( X ₁ – X ) и плоскостью переключения, тогда выполняется условие а( t )^( AX ₀ , Г ) = « о , то есть угол α ₀ – это угол максимального отклонения вектора ( X 1 - X) от ( Г , X ) = £ i , а(t ) ^ 0 при X ^ X 0 . Пусть при этом выполняется условие (12) при С = Г ₂, тогда величина ( AX , Г ₂) всегда имеет знак, противоположный знаку ( Г ₂, AX?) , следовательно, выполняется неравенство (14).

Из аналогичных соображений при С = Г ₃ cле-дует, что

V 3 ( X ) < 0 .                  (15)

Если при движении плоскости вида P_t первой достигает поверхности переключения точка X = X ₀, то тогда все аналогично с переобозначением X ₁ = X ₀. Здесь для геометрической наглядности рассмотрен случай n = 3, но все можно перенести на случай n > 3. Из неравенств (13), (14) и (15) следует, что V ( X ) <  0 .

Полученная матрица V по построению – идемпотентная и, следовательно, тождественна единичной матрице. Рассмотрим матрицу W = A^TV + VA , где матрица A – матрица нашей системы. Воспользуемся методом, позволяющим получать аддитивные свойства из известных мультипликативных (то есть используем кроне-керовскую сумму) [6], и следующим утверждением [4]: для отрицательной определенности матрицы W необходимо выполнение - S p W >|| W||_£ и достаточно, чтобы - SpW >  -jn -11| W ||_£. Это упрощенный критерий отрицательной определенности матрицы. Последнее неравенство в нашем случае представляется так:

Sp¹A > 2+^ Sp ⁽ AA > ■ ⁽¹⁶⁾

Условие (16) позволяет построить функцию Ляпунова для тех участков траектории, где расстояние измеряется в плоскостях вида Pt, и в целом позволяет построить функцию Ляпунова вдоль всей кусочно-гладкой замкнутой траектории.

В результате наших рассмотрений сформулируем

Предложение 3. Пусть выполнены все условия Предложения 2 относительно системы (1), (2), все собственные числа матрицы A имеют отрицательные вещественные части, ( Г , B ) ≠ 0 и выполнены условия (3), условие (12) для каждой точки переключения периодической орбиты и условие (16), тогда периодический режим является орбитально устойчивым периодическим решением системы (1), (2).

Отметим, что условие (12) можно рассматривать как дополнительное к свойству трансвер- сальности, а свойство (16) – как дополнительное условие на собственные числа матрицы A.

ЗАКЛЮЧЕНИЕ

Таким образом, получены достаточные условия существования изолированных периодических решений системы (1), (2), условие трансверсальности траекторий по отношению к поверхностям переключений, а также еще один вариант достаточных условий того, что периодическое решение является орби-тально устойчивым. Если возможно перейти к дискретному анализу системы (1), (2), то проблемы, рассмотренные в статье, не возникают [7].

PERIODIC ORBITS OF SAME CLASS RELAY RELAXATION OSCILLATORS