Person Authentication using Relevance Vector Machine (RVM) for Face and Fingerprint

Published Online May 2015 in MECS DOI: 10.5815/ijmecs.2015.05.02

Biometric-based personal authentication systems are estimated more reliable than traditional systems as their performance bases on a person’s physiological and behavioral  traits  which are always authentic  and secured[1], [2],  [3] while  traditional systems  use passwords, key, ID cards which can easily be lost, shared, stolen or even forgotten [4]. Currently available biometric systems use a variety of physical or behavioral characteristics such as fingerprint, facial thermo-grams, face, hand/finger geometry, iris, retina, gait, signature, voice pattern and hand vein to establish identity [3],[5] (Figure.1). Each Biometric trait has its own advantages and disadvantages; however, a biometric system would be considered admissible when it has these characteristics: universality, uniqueness, permanence, measurability, performance, acceptability and circumvention. [6].

Although uni-biometric systems, those using single biometric traits, are currently popular in use for their recent significant progress, they still suffer some drawbacks that impede their efficiency, namely noisy data, restricted degree of freedom, intra-class variability, non-universality, spoof attack and unacceptable error rates. However, with the feature of utilizing different biometric traits, such as different sensors, multiple samples of the same biometrics, different feature representations, or multi-modalities, multi-biometric systems can alleviate many of the limitations faced by uni-biometric system [7].

Multimodal biometric systems have gained intensive interest among designers and practitioners for two reasons. First, these systems perform better than uni-modal ones; second, their speed is improved satisfactorily. This leads us to the hypothesis that with the employment of multiple modalities (face and fingerprint), our proposed system would avoid the mentioned drawbacks of modality- based techniques.

According to Ross and Jain [7], in a multimodal biometric system, fusion can be performed at different levels, such as sensor, feature, matching score and decision. Among which [8] feature level fusion is usually considered difficult as different biometrics would have different feature vectors and different measures.

Support Vector Machine (SVM) classifiers have proven in the literature its outstanding performance of authentication tasks [9][10][11]. However, SVM requires sufficient amount of training data and a high number of support vectors for its performance, leading to expensive fusion. Regarding this, in this paper an authentication approach using Relevance Vector Machine (RVM) [12] is proposed. RVM is also like SVM - a sparse linearly parameterized model - but RVM requires fewer relevant vectors [12],[13]; hence, it increases the speed of the authentication process.

This paper presents a method using face and fingerprint traits and feature level fusion for the aims of finding effective ways to fuse at feature level of different characteristics, and constructing templates from the combined features. In our method, both face and fingerprint features are extracted using Zernike Moment (ZM)[14]. This moment is widely used because of its magnitudes are invariant to rotation, scaling and noise image, making the feature level fusion of face and fingerprints possible. Then, the authentication is done using RVM, based on the fused features.

The remainder of the paper mentions these contents: previous work in part 2, a description of the proposed method in part 3, reports and discussions of the experimental results in part 4, and the conclusion of the paper in the last part.

• II.    Previous work

One recent focus of interest in biometrics research is the successful combination of different sources of information resulting in the so-called multi-biometric. Fingerprint and face biometric authentication systems using state-of-the-art commercial off-the-shelf products are studied in [8] and it is confirmed that multimodal biometric systems outperform single biometric ones. In addition to examining well-known methods, a new normalisation and multimodal fusion method is introduced, based on matching score level fusion. The suggested normalisation and fusion methods are used for authentication applications that deal with open populations (e.g. airports).

Fusion of face and fingerprint in [15] considers the fingerprint quality information and is compared with four different fusion methods. The authors also showed that fusion of multimodal biometrics using data quality information outperforms standard multimodal results and unimodal systems.

Some state-of-the-art methods are studied in [16]. The concept of “uncertainty region” is proposed as a novel serial scheme. This system showed that the case of the first matcher is incapable to obtain enough evidence to classify the subject at matching scores. A simple mathematical model is used to simplify the design of the processing chain, and to compare serial scheme performance with the best individual matcher.

A novel system for identity authentication based on multi-route detection is presented in [17]. This system also uses face and fingerprint information, and it includes three modules: an enrolment module, an image preprocessing module and a fusion module. An SVM authentication fusion strategy distinguishes real clients from imposters, depending on self-learning results of the SVM from the enrolment module.

Multimodal biometrics in [18] uses a novel face and fingerprint fusion feature modelling approach, and explores the capability of ridgelet and discrete wavelet transforms coupled with different classifiers. The confidence values from the two classifiers are fused using various methods to decide the best method for classifier combination.

Advantages of using face and fingerprint biometrics simultaneously have appeared in a number of studies. The proposed multimodal biometric method in [19] is designed to enhance real time verification and reliability rates by going beyond the technical limitations of single biometric verification methods. Laplacian face is used for face recognition, DFB for fingerprint recognition, and an artificial neural network for the combination of those two.

A multimodal authentication model using face and fingerprint on space specified tokens is reported in [20]. Space specified tokens require little data and have been used to minimise the data storage. Face images are encrypted and encoded into fingerprint images. The verification accuracy provides a solution for spoofing and other attacks.

In one recent research in [21], a multimodal biometric system using face and fingerprint features with the incorporation of Zernike Moment (ZM) and Radial Basis Function (RBF) Neural Network for personal authentication is reported. It has been proven that face authentication is fast but not reliable while fingerprint authentication is reliable but inefficient in database retrieval, considering which our proposed system has been developed in such a way that it can avoid the advantages of those uni-modal biometric systems and acquire the variations in an individual’s image of face or fingerprint.

• III.    Methodology

Our proposed system consists of two stages: enrollment and verification. These two stages include face and fingerprint image preprocess, feature vector invariant extraction (with ZMI), feature fusion, and classification (with RVM). (Figure.2)

Faca and Fingerprint Image

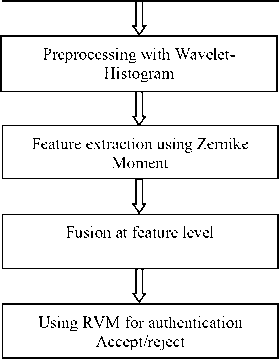
Fig. 2. The chart of the proposed system

• A.    Preprocessing

The pre-processing module aims at illuminating face and fingerprint images by reducing or eliminating some of their variations. In this stage, images are preprocessed before their features are extracted. In our multimodal authentication system, the image normalization, noise elimination, illumination normalization etc. are preprocessed using histogram equalization and wavelet transform [22], and features are extracted using Zernike Moment (ZM).

Wavelet transform [22] is a group of basic functions achieved when a basis wavelet is dilated and translated. Wavelets are concentrated in both time (spatial) and frequency fields due to their short-termed functions with finite support length (limited duration both in time and frequency). Thanks to its joint spatial-frequency resolution, wavelet transform is capable of extracting details and approximating images.

The two band wavelet transform, signal can be expressed by scaling and wavelet functions at different scales, in a hierarchical model. (Figure.3)

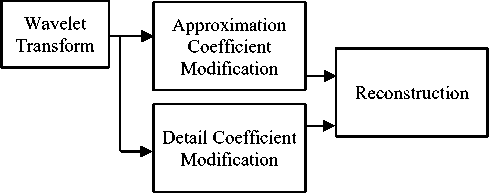
Fig. 3. The chart of wavelet transform obtained for authentication, and then two different feature domains- ZM for Face and ZM for fingerprint - are selected.

For a 2D image function f(x,y), the image can be changed from Cartesian coordinate into polar coordinate f(r,θ), in which r and θ symbolize radius and azimuth respectively. The following is the formulae to change an image from Cartesian coordinate into polar coordinate, r=√х +у            (2)

and

θ = arctan( )                 (3)

The unit circle (r ≤ 1) is defined on the image, and is enlarged with the basic functions V пт (r, θ) .

For a 2D image function f(x, у), the image is first changed into the polar coordinates and symbolized by f(r, θ) . The Zernike moment with order n and repetition m is defined as

Mпт =    ∫ ) ∫ [V пт(r, θ)]∗f(r, θ)rdrdθ (4)

in which * is complex conjugate, n is a nonnegative integer, m is an integer and n - |m| is nonnegative and even. The Zernike polynomial was defined over the unit disk as follows

Vпт(r,θ)=Rпт (r)e ime             (5)

with the radial polynomial R пт (r) is defined as

f(x) =∑к^а О, к∅ О, к(x)+∑j^∑кԁj , кψj , к(x)    (1)

where ∅ , , ѱ , are the scaling and wavelet functions at scale j. a , ,d , are scaling and wavelet coefficients.

Wavelet transform decomposes the derived image into several frequency components in multi-resolution. Using different wavelet filter sets and/or different quantity of transform-levels are likely to result in different decomposition outcomes. For our experiments, wavelets 1-level db10 was chosen; however, any wavelet-filters can be used in our proposed method.

• B.    Zernike Moment

The purpose of feature extraction is to extract the feature vectors or the image-representing information. In our system, feature extraction was done by Zernike Moment (ZM). Zernike moment (ZM) used for face and fingerprint recognition in our work is based on the global information, also known as statistical method [23], or moment based approach [24][25]. To enable an effective face and fingerprint authentication system, the chosen feature extractor needs to acquire the most relevant information about the face and the fingerprint to be recognized. In our system, from the derived images, different feature domains are extracted in parallel structure. Features of face and fingerprint images can be

(      |    |)

Rпт(r)=∑

(-1)(n-s)!

!. п₊ ^{|   |}    /!.     ^{|   |}    /!

The kernels of ZMs are set in right angles so the complex ZMs can represent any images. For all ZMs of an image, the image can be reconstructed as below.

f(r,θ)=∑п ∑₍All m's)Мпт Vпт (r, θ)        (7)

• C.    Feature extraction with Zernike Moment

Many experiments have proven that ZM performs better than other moments (e.g. Tchebichef moment [26], Krawtchouk moment [27]). In practice, we chose the first 10 orders of ZM with 36 feature vector elements for our experiments (Table 1). The quality of the reconstructed image will be reduced when the orders of ZM pass a certain value, due to a number of instability problems inherent with ZM.

Table 1. The chosen first 10 orders of ZMs

Order	Dimensionality	Zernike moments
0	1	M 00
1	2	M 11
2	4	M 20 , M 22
3	6	M 31 , M 33
4	9	M 40 , M 42 , M 44
5	12	M 51 , M 53 , M 55
6	16	M 60 , M 62 , M 64 , M 66
7	20	M 71 , M 73 , M 75 , M 77
8	25	M 80 , M 82 , M 84 , M 86 , M 88
9	30	M 91 , M 93 , M 95 , M 97 , M 99
10	36	M 10 0, M 10 2, M 10 4, M 10 6, M 10 8, M 10 10

Fingerprint Feature Extraction.

In our system, the fingerprint image is first enhanced by means of histogram  equalization and  wavelet transform. Then, features are extracted by Zernike Moments invariant (ZM). Each feature vector extracted from each normalized image is considered as feature descriptor in that it is used to represent the fingerprint. And to obtain a feature vector, that is, F(1) = (x1, ...., xn), where xn is feature vector elements 1 ≤ n ≤ 36, feature vector for the i-th user be Fi(1) = (x1, ..., xn). (Figure.4) Face Feature Extraction.

To capture feature vectors of size n, the given face image is normalized using histogram equalization and wavelet transform before it is computed by ZM. Let the result be the vector F⁽²⁾ = (v 1 ,. . . , v k ). Like the extraction of fingerprint features, where v_k is feature vector elements 1 ≤ k ≤ 36, feature vector for the i-th user is F_i⁽²⁾ = (v 1 , ..., v k ). (Figure.4)

Fig. 4. ZM for face and fingerprint feature extraction

Feature Fusion.

After feature vectors from fingerprint and face image of the same person (say, the i-th user) are obtained, the two vectors F i ⁽¹⁾ and F i ⁽²⁾ are combined into one, with the total feature vector of n+k component. The feature vector for the i-th user is F i = (u 1 , . . . , u n+k ), in which feature vector elements 1 ≤ n+k ≤ 72 are fused.

• D.    Classification

In our proposed system, RVM is used as a classifier in which the inputs to the RVM are the feature vectors produced by the feature fusion technique mentioned in the prior part.

RVM Description.

Owing to its superior generalization properties with a sparse kernel representation, the support vector machine (SVM) is considered a state-of-the-art technique for regression and classification; however, this technique still offers some disadvantages as the following:

• •    Predictions are not probabilistic. SVM produces a point estimate in regression, and a ‘hard’ binary decision, in classification. The estimation of the conditional distribution p(t|x) is necessary for capturing the uncertainty in a prediction, which in regression may take the form of ‘error-bars’. This estimation is also very important in classification where posterior probabilities of class membership need to adapt to various class priors and asymmetric misclassification costs.

• •    Although relatively sparse, SVMs make liberal use of kernel functions of which the essential number rises steeply with the size of the training set.

• •    The error/margin trade-off parameter ‘C’ (and in regression, the insensitivity parameter ‘ϵ’) needs estimating. This usually involves a cross-validation procedure, which is considered wasteful in terms of data and computation.

• •    The kernel function k(.,.) is required to meet Mercer’s condition.

Relevance vector machine is a special case of a sparse linear model for supervised learning models of the form:

y(x,w⁾ = S L1 WiФ i (x⁾ = w^тф(x) (8)

where weights matrix w = (w1, w2, . . . , wN)T, basis functions ϕ(x)=(ϕ1(x), ϕ2(x), . . . , ϕN(x))T and the output of RVM is a linearly-weighted sum of N. RVM is a Bayesian treatment of which does not suffer from any of the above limitations, as mentioned by Tipping [12]. Specifically, RVM is a fully probabilistic structure that posterior probabilitys of many of the weights are sharply peaked around zero. The term training vectors correspond to non-zero weights relevance vectors. The key feature of this approach is that in addition to offering good generalization performance, the inferred predictors are exceedingly sparse in that they contain relatively few non-zero wi parameters. The majority of parameters are automatically set to zero during the learning process, giving a procedure that is extremely effective at discerning those basis functions which are 'relevant' for making good predictions [12]. RVM is capable of classifier performance equivalent SVM but it uses fewer kernel functions.

Given a input-target pair {x n , t n }^N n=1 , two class is requested to predict the posterior probability of classes given the input x. Convention and generalise the linear model was used the logistic sigmoid function σ(y) = 1/(1 + e^-y) to y(x) and, adopting the Bernoulli distribution for P(t|w), the likelihood was written as

P⁽t|w) = П ,ri o[y⁽X n ,w)}^{t n} [1 - o{v⁽x_n,w)}|^: " ^{t n} (9)

with t={t1, . . ., tN} targets tnϵ{0, 1}. The aim is to find the ‘most probable’ weights wMP that maximizes the probability P(t|w). This is done by Laplace’s approximation method [28]. The ‘most probable’ weights wMP can write:

∑=(ΦтΒΦ+A)-1

wMP =∑Фт Bt

where A = diag(α1, α2, . . . , αN) and B = diag(β1, β2, . . . , βN) are diagonal matrixs with α a vector of hyperparameters and βn = σ{y(xn)}[1-σ {y(xn)}]; Σ is the posterior covariance matrix for a Gaussian approximation to the posterior over weights centered at wMP. Repeating this process until a convergence criteria is met. The hyper-parameters resulted by the above method used estimate of target values for the input x’ follow as у=wMPϕ(x ) (12)

Classification

The achieved feature vector element set, equal to 72 for each object, correspond to input data set of RVM. The authentication using RVM is performed in two phases: training and testing. (Figure 5)

In the training phase, let set (x i , t i )^N i=1 where N is the number scores in the training set, t i ∈ {0, 1} = {impostor, genuine}, a function transforming f : ℜ ^’ → ℜ is applied to x, so as to separability of genuine and impostor fused scores. Φ(x) is the design matrix with Φ = [ ϕ (x₁), ϕ (x₂), . . ., ϕ (x_N)]^T as the input to the classifier. The training data set consists of {x n , t n }^N n=1 (N= 72; t n ∈ {0, 1}). The proposed approach mentioned above processing the relevance vectors (kernel functions) by a prior on hyperparameter α. With given α values, the most probable weights (w_MP) are found. During the training, the relevance vectors model and the most probable weights {R,w MP }are found.

In the testing phase, the function, {R,w MP }, is used to predict the genuine or impostor class for the testing set defined by x’ using equation (12). Then, the corresponding output value (y j ∈ {0, 1}) for each classifier is identified using the j^th vector and weight {R^j,w^j MP }. Finally, the extracted features are classified using RVM, resulting in the range in which zero (reject) and one (accept).

Fig. 5. Illustrating multimodal authentication

• IV.    Experimental Results And Discussion

• A.    Databases overview

  In practice, our experiments were conducted using fingerprint images dataset DB4 FVC2004 [29] and ORL face database [30] - two public domain databases.

Dataset DB4 FVC2004 has 800 fingerprints of 100 fingers; for each finger 8 instances. Fingerprint image with a size of 288x384 pixels, and its resolution 500 dpi. (Find the sample fingerprint images dataset DB4 FVC2004 in Figure.6)

Fig. 6. Captured fingerprint images in dataset DB4 FVC2004.

ORL face database consists of 400 images from 40 different people, for each person 10 images. The images contain variations with facial expressions or configurations such as open eyes, close eyes, smiling, non-smiling, wearing glasses, without wearing glasses. These images have a size of 92 x 112 pixels with dark background. Some sample face images in ORL database are depicted by Figure.7

Assuming that combining images(face and fingerprint) in pairs, namely, ORL-FVC database is comprised of 320 double images from 40 different individual, for each person 8 double images (8 face images in ORL and 8 fingerprint images in FVC). We obtain our own database for our experiments.

Fig. 7. Example face images in ORL face database

• B.    Evaluation

In our work, a proposed system including two different feature domains with the RVM classifier was developed. In this system, concerning the Zernike Moment, the first moment 10 orders were chosen as feature vectors, and the number of combined feature vector elements for these domains is 72. The recognition performance of the proposed method on ORL-FVC database was evaluated. The training was done with 30 percent images of ORL-FVC database (12 individuals – 12 x 8 x 8 = 192 images, each person 8 face and 8 fingerprint images) including 96 double images. The remaining images pertaining to 28 individuals (70 percent) used for testing include 224 double images for RVM. Due to the limited number of images of the ORL-FVC database, this train-test partitioning was used to perform the trial over three times for cross validation to get the average authentication rate.

Three different training sets and test sets were used for our experiments. The mean authentication rate we could achieve from our experiments is 98.72% (Table 2).

Table 2. Recognition rates achieved by our proposed method

Test	Rate
1	98.75%
2	98.58%
3	98.83%
Mean	98.72%

The proposed method was also compared with the unibiometrics, particularly face recognition system [31], fingerprint recognition system [32]. The ZM of these systems has first 10 orders with 36 feature elements. The comparative results of uni-biometrics in Table 3 demonstrate that the recognition rate of our multimodal system can perform the recognition tasks better than mono-modal systems.

Table 3. The Accuracy rates of the uni-biometrics

Characteristic	FRR(%)	FAR(%)	Rate
Face[31]	13.47	11.52	73.20
Fingerprint[32]	7.151	7.108	92.892

Also, separated experiments base on the RVM, SVM technique for mono-modal (face, fingerprint) and face, fingerprint fusion at feature level were conducted. In these experiments, the accuracy in recognition of our proposed method was compared to that of each technique mentioned above, and the achieved comparative results again indicate the striking usefulness and utility of the proposed method. The receiver operating characteristics (ROC) curves of the face and fingerprint along with fusion algorithms can be seen in Figure 8, and the average verification accuracies at 0.01% FAR is presented in Table 4.

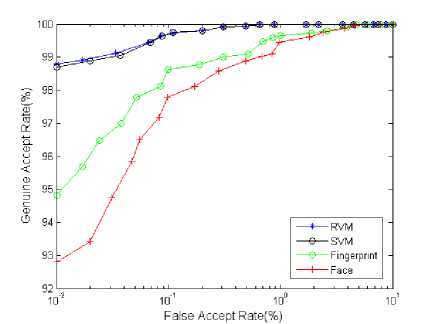
Fig. 8. ROC curves of the proposed RVM, SVM, face and fingerprint

Statistically, very little difference can be seen in the results achieved between SVM and RVM fusion; however, apparently, around three times of trials, SVM requires more kernel functions (support vectors) than RVM. Moreover, as the proposed RVM algorithm utilises less relevant vectors, around three times it requires fewer computations than SVM, leading to faster testing. The number of kernel functions (vectors) utilised by SVM and RVM and their testing time are displayed in Table 4. Furthermore, RVM method utilises fewer parameters than SVM. In our experiments, using Gaussian for kernel achieves the best accuracy over three trials.

Table 4. Time (milliseconds) and the number of vectors utilised for classification of SVM, RVM

	Number of vectors	Time (ms)
SVM	22	0.09
RVM	4	0.02

• C.    Discussion

From the experimental results, some significant features of the proposed system using Zernike Moment (ZM), Relevance Vector Machine (RVM) descriptor can be seen as below.

ZM algorithm brings us these benefits:

• ❖    ZM algorithm enables a face-fingerprint recognition system to work on images of various shapes as its performance is based on the identified center of the image. Also, this algorithm can provide feature sets with similar coefficients for easy computation.

• ❖    ZM is invariant to rotation, scale and translation.

RVM has many properties and among them the most important ones are the following:

• ❖    RVM is a Bayesian treatment of a generalised linear model of functional form identical to the Support vector machine (SVM) – a state-of-the-art technique for regression and classification.

• ❖   RVM requires dramatically fewer kernel functions

than SVM.

• ❖   RVM needs less time for computation and thus

works faster than SVM.

• V.    Conclusion