Перспективы использования кластерного и дисперсного анализов при проектировании сетей инженерно-геологических изысканий на намывных техногенных массивах

Комплексные инженерно-геологические изыскания (ИГИ) в нашей стране начинают свою историю с рубежа XVII и XVIII веков. На первоначальных этапах в России проводились отдельные исследования поверхностных отложений с применением технических средств, явившихся прообразами современных пробоотборников. Имеются сведения об изучении Петром I грунтов дна Каспийского моря. В XIX столетии работая как изыскатели, геологи применяли различные методы исследований: маршрутные наблюдения, проходку шурфов и шахт, ручное бурение, лабораторные испытания грунтов. Оценка физико-механических свойств грунтов в полевых условиях производилась по характеру и глубине внедрения в них заступа, лопаты, кайла, лома, клиньев, стального сверла [5].

Однако только в 1937 году Ф. П. Саваренский впервые дал систематическое описание методов инженерно-геологических исследований и сделана попытка обосновать целесообразность двух стадий инженерно-геологических изысканий. В отличие от чисто прагматического геотехнического подхода (исследования свойств грунтов в основании сооружений), свойственного иностранным специалистам, отечественная школа инженерной геологии всегда считала важнейшей задачей разработку научно обоснованной методики инженерно-геологических исследований [1].

Несмотря на более чем 70 летнюю историю ИГИ к сегодняшнему дню не создано ни одной научно обоснованной методики их проведения. Рекомендации по размещению пунктов получения информации (скважин, горных выработок и др.) на объекте исследования, содержащиеся в нормативных документах (ГОСТах, СНиПах и СП), регламентирующих методику инженерно-геологических исследований для намывных массивов, научно не обоснованы. Они не учитывают свойства геологической среды, в том числе свойства грунтов и их пространственную изменчивость [1, 2].

Применительно к намывным объектам горнодобывающей промышленности наиболее перспективным является применение комбинированных методов, опирающихся на опыт проведения исследований на предыдущих этапах и способы современной статистики. При этом производится моделирование намывного сооружения и на каждой итерации происходит уточнение полученной модели. Наиболее существенным отличием данного подхода от применяемых на сегодняшний день является квазиодновременное (в условиях данной задачи считаем, что все действия произошли одновременно и независимо друг от друга) исследование всего массива за один этап - границы всех зон при районировании определяются параллельно. Мониторинг технико-физических показателей массивов является своего рода регулятором построенной системы. Такого рода подход позволит значительно сократить объемы натурных (наиболее емких по времени и капиталовложениям) изысканий за счет оптимизации сетей инженерно-геологических изысканий.

Для определения положения границ зон районирования используются принципы кластерного и дисперсного анализа. Обработка полученных результатов на основе факторного анализа позволяет выявлять наиболее значимые параметры районирования и оценивать погрешность. Важно отметить, что все алгоритмы кластеризации подчиняются гипотезе компактности, т.е. “в используемом базисном пространстве объекты, принадлежащие одному и тому же классу, максимально близки между собой, а объекты, принадлежащие разным классам хорошо разделимы друг от друга”. Уместнее говорить о достаточной разнице между центрами кластеров, так как различие между двумя объектами, принадлежащими соседним классам, может быть меньше, чем между двумя объектами одного класса. Исходя из упомянутого выше принципа компактности, уместно ввести количественную оценку качества кластеризации объектов. Простейшей оценкой будет отношение суммы дисперсий в каждом классе к дисперсии между центрами всех классов [3,4]:

0 = ,где

И

Q - дисперсия между центрами кластеров.

Так как на начало проведение анализа центры конечных кластеров не известны воспользуемся иерархическим методом. Это группа, характеризующаяся последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров. В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге наиболее похожие объекты объединяются в кластер. На последующих шагах объединение продолжается до тех пор, пока все объекты не будут входить в один кластер или в заданное их число.

При объединении объектов возникает проблема определения положения новой группы относительно других. Введем понятие центра кластера, как точки в многомерном пространстве (как правило, в заданном наборе данных она не существует), которая отражает средние значения параметров объектов, вошедших в кластер.

Воспользуемся методом наименьших квадратов для поиска центра нового кластера. Опишем функцию ε(х _с ), которая показывает зависимость изменения суммы квадратов расстояний от точек кластера до искомого центра х _с . Так как рассматриваем n – мерное метрическое пространство, то в проекциях на оси квадрат расстояний можно выразить следующим образом:

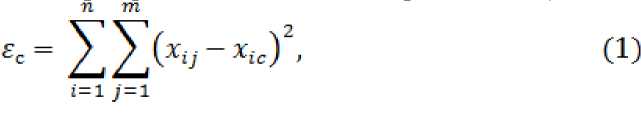
где n – мерность пространства, m – количество точек в кластере, х ij – проекция j ой точки на i ^ую ось, х ic – проекция искомого центра на i ^ую ось.

Найдем минимум данной функции, для этого запишем частные производные по всем переменным хi:

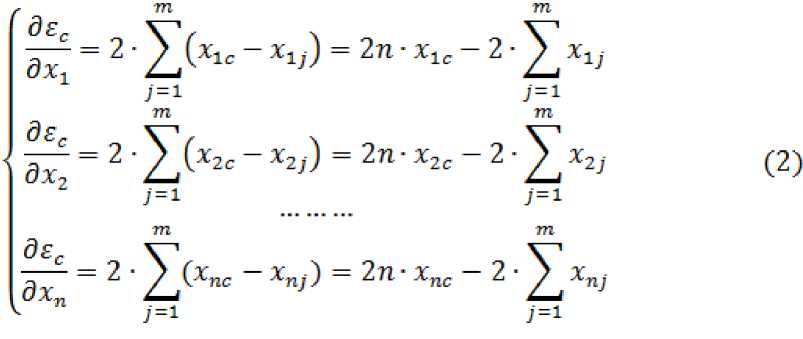
Из необходимым условия существования экстремума у функции

нескольких переменных получим:

Из критерия Сильвестра получаем, что в данной точке находится минимум функции.

На основе получаемых центров кластеров проведем проверку, которая позволит определить необходимость дальнейшего сгущения сети. Критерием при этом выступает величина ξ, полученная как усредненная сумма по каждому наблюдаемому параметры и кластеру: п т

1 X ’ 1 \ ’ 1^12 ^ill nZ-rmZ—i %i2 + ^ii i=l j=l где n – количество кластеров;

• m – количество наблюдаемых параметров;

• x i1 – значение i-го параметра на предыдущем шаге;

• x i2 – значение i-го параметра на текущем шаге.

Также в качестве критерия прекращения сгущения сети может выступать графически вычисленная величина τ, равная отношению изменения площади выделенной зоны ΔS на гидроотвале к площади этой зоны S:

ZIS

При этом сеть считаем построенной, если ξ и τ не превышают 5%, для второй величины необходимо выполнение условия для всех зон.

Разработанная математическая модель отличается гибкостью, соответственно легко расширяема. Любой из этапов нормирования данных или разбиения объектов на кластеры может быть заменен другим статистическим способом, что позволяет применять полученный метод для различных объектов, обладающих пространственной изменчивостью, также данная математическая модель может быть основой для создания современных САПР в горной промышленности и других отраслях народного хозяйства.