Перспективы методов вычислительной гидродинамики при исследовании мембранных процессов

При математическом моделировании мембранных процессов изучение структурных особенностей используемых мембран и существенная ограниченность информации при формальном описании их разделительных свойств привели к разработке физических моделей, учитывающих не только особенности строений реальных мембран, но и их особенностей функционирования.

Любая физическая модель мембранного процесса, ввиду его сложности, не отражает всех сторон явления (вследствие хотя бы чрезмерной громоздкости конечных аналитических выражений). Также, модель проверяют на реальных физико-химических объектах (мембрана и культуральная жидкость), возмущаемых налагаемой разностью химического потенциала (градиент давления и концентрации по обе стороны мембраны), т. е. система принципиально неравновесна и, в лучшем случае, стационарна.

Особенности реализации физических моделей на конкретных технологических жидкостях весьма разнообразны, что часто приводит к достаточно неожиданным результатам и, поэтому, они находятся в центре внимания многих исследователей.

При составлении физических моделей мембранных процессов, невозможно объективно провести количественный учет большинства факторов из-за их большого многообразия и изменчивости, что далеко отдаляет математическую модель от реального процесса.

Именно поэтому методы вычислительной гидродинамики надежно и эффективно выполняют расчеты для всех физических моделей и типов, включая стационарное или переходное течение, несжимаемое или сжимаемое течение (от малых дозвуковых до гиперзвуковых), моделирование ламинарных или турбулентных потоков, ньютоновских или неньютоновских жидкостей, идеального или реального газа.

На данный момент в мире существует ряд универсальных коммерческих программных продуктов для решения задач вычислительной гидродинамики. Среди ведущих зарубежных коммерческих пакетов можно выделить такие, как «ANSYS FLUENT» и «ANSYS CFX» корпорации ANSYS Inc, «STAR-CD/STAR-CCM+» компании CD-adapco Group, позволяющие проводить моделирование широкого класса физических процессов в научных и инженерных областях. Существуют и отечественные универсальные коммерческие пакеты: Flow Vision компании ТЕСИС, Gas Dynamics Tool компании GDT Software Group.

В основе данных методов находится комплекс программ, подходящих для проектирования, расчетов и решения проблем, связанных с описанием потоков жидкости внутри мембранного модуля.

Для полноценного изучения сложных физических явлений, в особенности одновременного протекания мембранного и биотехнологического процессов, необходимо проведение на практике большого количества дорогостоящих экспериментов, чего можно избежать благодаря моделированию с помощью методов CFD [1–6].

Известно, что образование на поверхности мембран гелевого слоя, в котором концентрация растворенного вещества больше, чем в основном объеме раствора, носит название концентрационной поляризации. Отрицательное воздействие данного явления на мембранные процессы разделения и концентрирования вызвано следующими аспектами:

• •    уменьшается перепад давлений над и под мембраной, т. к. растет осмотическое давление исходной жидкости, сопровождающееся уменьшением удельной проницаемости и избирательной задерживающей способностью мембран;

• •    сокращается эксплуатационный период использования мембран, определяющий, в конечном итоге, стоимость мембранного процесса.

Для оценки уровня концентрационной поляризации на поверхности мембран, выяснения характера и механизма гелеобразования также могут быть использованы методы CFD [7]. Кроме того, можно посчитать крутящие моменты, силу механического сдвига и влияние вязкости жидкости на гидродинамику потоков через мембрану. Например, в работе [8] с помощью методов CFD изучен эффект влияния геометрической формы микроопор мембран на гидродинамику потоков культуральной жидкости. В работе [9] методами CFD авторы исследуют области мембраны, которые наиболее склонны к гелеобразованию. В исследовании [10] авторы на основании полученной CFD-картины процессов и явлений прогнозируют механизм оседания частиц на мембранную поверхность мембраны.

Таким образом, CFD-моделирование является одним из перспективных инструментов исследования и оптимизации мембранных процессов, протекающих с участием жидких и газовых потоков в пищевом, химическом и биотехнологическом производствах [11].

Следует отметить, что, несмотря на очевидные преимущества CFD-программного комплекса, все же не стоит пренебрегать экспериментальной проверкой результатов моделирования для более точной оценки адекватности математической модели.

Методы

Рассмотрим основные принципы, заложенные в математическое моделирование с помощью методов CFD.

Решатель «ANSYS FLUENT» основан на методе конечных объемов, при этом: область течения разделяется на конечное множество контрольных объемов; в этом множестве контрольных др    д vx    dVy    dvz

--+ р --+ р --+ р — — — J ; дт    д x      д у      д z

объемов решаются уравнения сохранения массы, импульса, энергии и т. д.; уравнения в частных производных дискретизируется в систему алгебраических уравнений; затем производиться численное решение этих алгебраических уравнений в расчетной области.

Приведем конкретный пример, основанный на изучении работ [12–15].

Уравнения для расчёта гидродинамических условий внутри полых волокон мембранного биореактора. Основные уравнения, используемые для описания потоков, являются уравнение сохранения массы и импульса, которые для нестационарных условий имеют следующий вид:

д рv_Y        д v_x       д v_r       д v_Y

-+v + v р + vv р   + Vz р   — xyz дт       дx       ду       дz дP    ( д2 vx   д2 vx   д2 vx дx     v дx2    дy2    дz2 ;

+ р д ;

дрVy,      д v       9v

+ vx р — + vy р — + Vz р^ = дт       дx       ду дP    (92 Vy   д 2 vy

+ ц++ ду    ^ дx2    ду2    дz2

др v       д v       д v       ду

--- + vr р-- + vx р —- + v7 р —- — xyz дт       дx       дy      дz дP    ( д2 v   д2 v д2 v )

• —+ р       ++ ;

д z     ( д x ²     д y ²     д z ² _v

где ρ – плотность культуральной жидкости, кг/м³; v Х , v у , v z – скорость кульуральной жидкости вдоль осей OX, OY и OZ соответственно, м/с; g – ускорение свободного падения м/с²; J – поток культуральной среды, переходящий из внутриволоконного пространства в межволоконное через мембрану, кг/(м×с²); Р – давление, Па; μ – динамическая вязкость культуральной среды, Па×с; τ – продолжительность процесса; с; x, y, z – координаты, м.

В правой части уравнений (1)–(4) находятся параметры, описывающие изменение импульса за счёт градиента давления и за счёт сил вязкостного трения. Третий параметр в уравнении (2) описывает изменение импульса за счёт силы тяжести.

Поток культуральной жидкости, прошедший через мембрану, описывается уравнением Хагена-Пуазейля следующего вида:

J — ^

s r ^ S р^ P _

8 р5Т  ’

О, при x1 Хм i, y1 y м i, z1 z м, где ε – количество пор на единицу поверхности мембраны, 1/м2; rn – средний радиус пор, м; S – площадь поверхности мембраны, м2; δ – показатель кривизны пор; T – толщина мембраны, м.

Начальные и граничные условия для внутриволоконного пространства мембранного биореактора имеют вид:

^v ( xm, У ст ,z m ) ^{— 0 (6)}

v (xx, Ух,, zx)—v ex;

P (x6Xy6Xze)\—^ Px;(8)

ox, ox, oxox v (t — 0) — v 01;

р( t — 0) — ро1-

Граничное условие (6) определяет условие прилипания культуральной жидкости к непроницаемым стенкам биореактора, а условие (7) определяет скорость культуральной жидкости на входе во внутриволоконное пространство мембранного биореактора. Условие (8) задает давление культуральной жидкости на входе в мембранный биореактор.

Уравнения для расчета гидродинамических условий в межволоконном пространстве мембранного биореактора. Для межволоконной области основными уравнениями, по аналогии с (1)–(4), также являются уравнения сохранения массы и импульса, уравнения (11)–(14).

dp    d v x     ^{d v}y     d v z

--+ p --+ p --+ p — — I + J ;

дт    д x     д y     д z

dp v y -   + Vx p дт	д v        d v y       д vv —- + v, p —- + v_ p—- — д x       д x       д x
д P — ---+ Ц д У	(        ^2     ^2  A д 2 V x , д v y , д v y ^ д x2     д y2     д z2 ^	;

д p v       д v      д v       д v --- + v x p — x + v y p — x + v z p —- — дт       д x    y   д x       д x			(12)
д P —-a x+^	' <>2        ^2        <^2 A д vv    д vv    д vY ++ д x2     д y2     д z2?	+ p g ;
дp v7        д vY        д vy       < - + vY p - + v.,p —- + v p xyz дт       д x       д x		9 v^ = д x
д P — ---+ p д z	^д2 v,    д2 vy   д2 vz x + y + z_ ^ д x2     д y2    дz2	';	(14)

В правой части уравнения (11) находятся слагаемые, описывающие приток массы за счёт потока культуральной жидкости, перетекающей из внутриволоконного пространства в межволоконное, и убыль массы за счёт поглощения клетками питательных веществ, необходимых для их жизнедеятельности. Приток массы, перетекающей из внутриволоконного в межволоконное пространство, описывается выражением (5).

Количество массы, потребляемое клетками, рассчитывается:

N

I — J q ( t ) dt              (15)

где N – число клеток; q с – скорость потребления питательной среды одной клеткой.

Набор начальных и граничных условий для системы уравнений межволоконного пространства мембранного биореактора имеет следующий вид:

v (xcm,Уст,zcm ) — 0(16)

v (xex, у xx, zex) — vi;

PUxy«xZ«x)—P;(18)

• xx, xx, xxa

v (t — 0 ) — v 02;

p( t — 0) — p02-

Граничное условие (16) определяет условие прилипания культуральной жидкости к непроницаемым стенкам биореактора, а условие (17) определяет скорость среды на входе в межволоконное пространство биореактора. Выражение (18) задает давление среды на выходе из межволоконного пространства биореактора [12–15].

Результаты

В качестве мембранного биореактора для физического эксперимента авторами [12–15] использовался модуль на основе полых волокон С2008 FiberCell System. Технические характеристики биореактора указаны в таблице 1.

Таблица 1.

Техническая характеристика мембранного биореактора С2008 FiberCell System [12–14]

Table 1.

Technical characteristics of the membrane bioreactor С2008 FiberCell System [12–14]

Наименование параметра	Показатель
Количество полых волокон	60
Диаметр полого волокна, мкм	700
Диаметр полого волокна, мкм	1300
Толщина полого волокна, мкм	300
Длина полого волокна, мм	110
Диаметр корпуса, мм	220
Длина мембранного модуля, мм	130

Мембранный биореактор С2008 FiberCell System представлял собой картридж (рисунок 1), заполненный полыми волокнами. Волокна имели различные диаметры пор для диффузии молекул с молекулярной массой 5 кДа, 20 кДа и более.

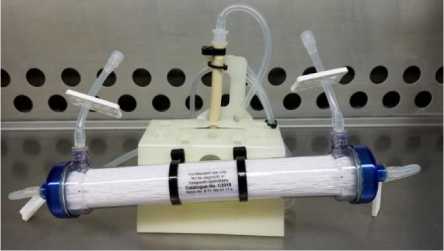
Рисунок 1. Мембранный биореактор С2008 FiberCell System

Figure 1. Membrane bioreactor Since 2008 FiberCell System

Культуральная среда прокачивалась через полые волокна и обеспечивала рост клеток в ограниченном пространстве на их поверхности. Полые волокна создавали полупроницаемый барьер с заданными свойствами между пространством, где культивировались клетки, и протекающей средой.

В процессе секретирования продукты концентрировались в малых объемах межволоконного пространства, где их концентрация могла достигать значений в 100 раз больших, чем при проведении аналогичного процесса в колбах или в роллерных бутылях.

Обсуждение

Авторами [12–14] было проведено CFD-моделирование гидродинамических условий в мембранном биореакторе на основе полых волокон при полном их заполнении клетками и с учетом рассчитанной величины коэффициента проницаемости мембраны.

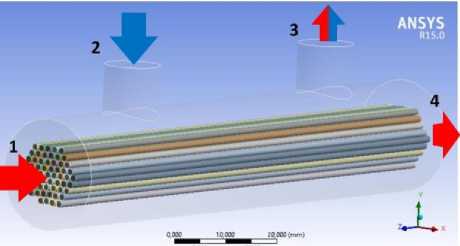
На основании предложенного автором [12] ранее прямоточного режима подачи питательной среды в межволоконное пространство относительно внутриволоконного, входными являются патрубки 1 и 2 (рисунок 2), выходными 3 и 4. Красным цветом указаны потоки питательной среды во внутриволокон-ном пространстве, синим цветом – потоки в межволоконном пространстве.

5,000           15.000

Рисунок 2. Схема движения потоков питательной среды в половолоконном мембранном биореакторе (по данным Сафарова Р. Р.) [12]

• Figure 2.    Scheme of the movement of nutrient medium flows in a hollow-fiber membrane bioreactor (according to R. R. Safarov) [12].

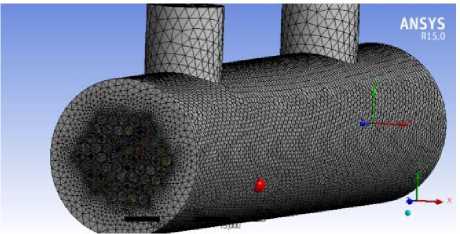
Рисунок 3. Сеточная модель половолоконного мембранного биореактора (по данным Сафарова Р. Р.) [12]

• Figure 3.    Grid model of a hollow-fiber membrane bioreactor (according to Safarov R. R.) [12]

Расчетная сетка биореактора с 60-ю волокнами содержала 12 млн ячеек с минимальным размером ячейки в зоне повышенной плотности сетки, равным 0,1 мм (см. рисунок 3).

В результате расчета автором [12] получено скоростное распределение движения потоков в межволоконном пространстве. Для 2-x дней культивирования гидродинамика потоков представлена на рисунке 4, анализируя который можно сделать вывод о равномерном распределении потока в большей части биореактора.

Рисунок 4. Схема распределения скоростей потоков в межволоконном пространстве половолоконного мембранного биореактора для 2-х дней культивирования (течение среды – слева направо (по данным Сафарова Р. Р.) [12]

• Figure 4.    Scheme of the distribution of flow rates in the interfiber space of a hollow fiber membrane bioreactor for 2 days of cultivation (the flow of the medium is from left to right (according to Safarov R. R.) [12]

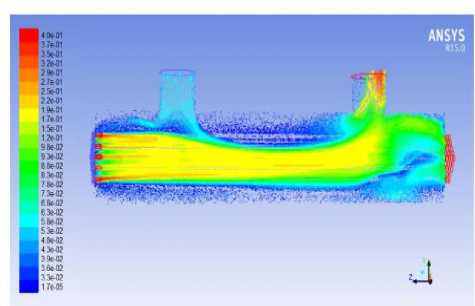
Рисунок 5. Схема распределения скоростей потоков в межволоконном пространстве половолоконного мембранного биореактора на 8-ой день культивирования направо (по данным Сафарова Р. Р.) [12]

• Figure 5.    Scheme of the distribution of flow rates in the interfiber space of the hollow fiber membrane bioreactor on the 8th day of cultivation to the right (according toSafarov R. R.) [12]

Визуализация гидродинамической картины для последнего этапа культивирования отражена на рисунке 5. В левой части мембранного биореактора, а также в центральной области между боковыми патрубками автором [12] наблюдались области низких скоростей. Однако, рассчитанная минимальная скорость потока в межволоконном пространстве меньше скоростей в рассматриваемых областях, поэтому автором [12] сделан вывод об отсутствии застойных зон на первых этапах культивирования.

Автором [12] отмечены области, в которых скорость имела максимальное значение (рисунок 5). Данные области относились к зоне входа питательной среды во внутриволоконное пространство биореактора, а также к зоне выхода питательной среды из межволоконного пространства (патрубок 3 , рисунок 2). По мнению Сафарова Р.Р., данные зоны не содержали поверхности с прикрепленными клетками, поэтому рассматриваемые скоростные пики не оказывали пагубного влияния на процесс [12–15].

post@vestnik-vsuet.ru Заключение

В рассмотренном выше примере, авторами [12–15] проведен наглядный анализ возможности использования вычислительной гидродинамики CFD для расчета гидродинамики потоков в мембранном биореакторе на основе полых волокон. Авторами [12–15], в частности, Сафаровым Р.Р. была построена электронная геометрическая модель установки, осуществлен выбор геометрии сетки с различной плотностью для оптимизации времени расчетов и точности решения для конкретного случая, рассчитана кинетическая зависимость роста клеток, определены расходы подачи питательной среды во внутриволоконное и межволоконное пространства биореактора, проанализированы гидродинамические условия.

Все вышесказанное подтверждает перспективы использования CFD-методов для моделирования мембранных процессов, осложненных культивированием клеток на поверхности мембран.