Перспективы применения методов многомерной геометрии для оптимизации процесса склеивания деталей швейных изделий

Процессы склеивания деталей швейных изделий занимают незначительный объем по трудоемкости изготовления одежды (0,9 – 6,5 %), однако именно в этих процессах заложены максимальные резервы роста производительности труда и улучшения качества изготавливаемой одежды.

Клеевые процессы протекают по сложным физико-химическим законам, при этом большое количество управляемых и неуправляемых факторов влияют на качество получаемого соединения. Очевидно, что выбор оптимальных параметров режимов склеивания является многофакторной задачей.

Для изучения и анализа технологического процесса склеивания широко применяют методы оптимизации [1, 2]. Использование таких методов дает возможность более эффективно управлять технологическим процессом, определять пара- метры его устойчивой работы, организовать поиск условий для получения наилучших результатов. Оптимизация технологического процесса склеивания позволяет значительно повысить производительность используемого оборудования и улучшить качество выпускаемой продукции.

При решении задач оптимизации данного процесса широко используются методы математического моделирования. Один из наиболее часто встречающихся методов решения - метод математического планирования эксперимента. Он позволяет проводить оптимизацию технологических процессов по некоторому набору параметров и связан с проведением серии опытов, количество которых пропорционально количеству параметров. Поэтому данный метод обладает рядом недостатков, связанных с большими временными и финансовыми затратами. Кроме того, он рассмат- ривает процесс как черный ящик и не позволяет узнать о протекающих в нем явлениях.

При исследовании многофакторных процессов и обработке многомерных данных наряду с абстрактными аналитическими моделями используются модели геометрические. Одним из важных достоинств геометрических моделей является возможность получения наглядных представлений об изучаемых явлениях.

С точки зрения геометрии клеевой процесс должен быть представлен в пространстве размерности не менее пяти, так как прикладная задача требует установления взаимосвязи большого числа параметров процесса с двумя и более показателями качества.

В начертательной геометрии существуют различные способы представления многомерного пространства и построения чертежей многомерных объектов на основе проекционного аппарата. Вместе с тем, по мере увеличения размерности моделируемого пространства, конструктивный метод становится менее наглядным, и все обоснования проводятся формализованными методами вычислительной геометрии. Наиболее удобной для решения задач оптимизации различной степени сложности принято считать модель многомерного пространства -чертеж Радищева [3]. Данная модель позволяет формализовать полученные на ее основе модели конкретных систем и процессов, что дает возможность автоматизировать построение чертежей.

Совершенствованию, развитию и применению чертежа Радищева в области исследования многофакторных процессов посвящены работы В. Н. Первиковой, Н. Ф. Четверухина, В. Я. Волкова, В. Ю. Юркова и других [4 - 8]. Их анализ показывает, что методы многомерной геометрии на основе чертежа Радищева успешно применяются к моделированию многофакторных многокомпонентных систем в физико-химическом анализе, при этом для исследования свойств многокомпонентных систем используются методы вычислительной геометрии и методы теории параметризации.

Однако, несмотря на множество разработок в данном направлении, остается актуальным вопрос о достоверности решения задач на указанной модели (чертеж Радищева), отсутствуют алгоритмы решения задач оптимизации многофакторных процессов и программное обеспечение для автоматизации построения чертежей геометрических оптимизационных моделей.

С целью создания оптимизационных моделей многофакторных процессов авторами исследованы варианты задания элементов на чертеже Радищева и выполнен формализованный анализ решения позиционных задач, что позволило разработать конструктивные модели поверхностей и гиперповерхностей различного вида для моделирования многофакторных процессов и алгоритмы построения области пересечения гиперповерхности с гиперплоскостью уровня.

На базе сформулированных в работе [9] теоретических основ алгоритм построения области пересечения гиперповерхности с гиперплоскостью уровня реализуется следующим образом: гиперповерхность описывает зависимость оптимизирующих факторов от компонентов системы (факторы, параметры технологического процесса), а гиперплоскость уровня задает требуемое значение оптимизирующего фактора.

Алгоритм определения области оптимизации трех компонентов в зависимости от значений трех оптимизирующих факторов покажем на примере трехкомпонентной системы ( x 1 , x 2 , x 3 ) с тремя оптимизирующими факторами φ, χ, f (рис. 1).

Гиперповерхности оптимизирую щих факторов φ, χ, f заданы семействами 1-поверхностей двойного уровня  χ1

(Х11,Х12,Х13), Х2(Х21,Х22,Х23), Х3 (Х31,Х32,Х33); Ф1 (фП,ф12,ф13),         Ф2         (ф21,фЧф23),

Ф3 (Ф31,Ф322,Ф33);f(7 ",/'',/'3).f..а21/2/3), f$ (/ ,/ ,/ ) соответственно; оптималь ные значения факторов Хоптим, фоп™ и f0птим заданы гиперплоскостями уровня. В данном случае областью оптимизации будет являться 0-плоскость, так как число компонентов равно числу оптимизирую- щих факторов. Определение области оп-      алгоритму.

тимизации произведем по следующему

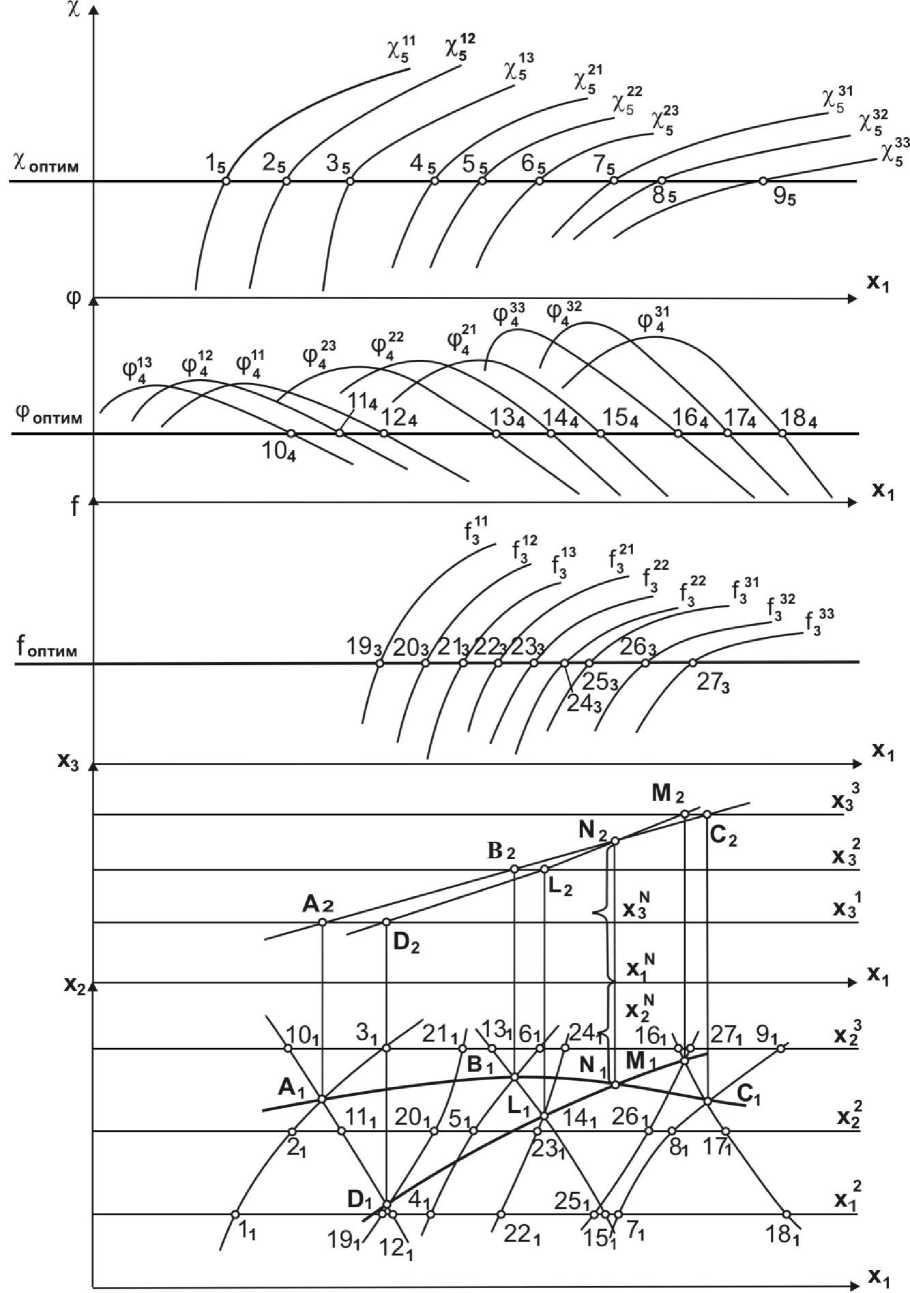
Рисунок 1 - Схема алгоритма

1. Рассматривая расслоение гиперповерхностей оптимизирующих фак-

торов, следует принять один из компонентов постоянной величиной - x 3 ¹, при этом компоненты x 1 и x ₂ варьируются; если принять, что компонент х₂ изменяется дискретно, принимая три значения х 21 , х 22 , х 23 , то, варьируя компонент x 1 , получим 2-поверхности χ¹¹ ,χ¹² ,χ¹³ ; φ¹¹,φ¹²,φ¹³; ƒ ¹¹ ,ƒ ¹² ,ƒ ¹³ оптимизации трех факторов для каждого значения компонента х 2 .

• 2.    Зададим оптимальные значения факторов Х оптим , ф оптим и f >п™ , которые геометрически представляют гиперплоскости уровня, и получим 1-поверхности пересечения 2-поверхностей с заданными гиперплоскостями уровня -1 2 3 (1 5 2 5 3 5 , 1 1 2 1 3 1 ), 10 11 12 (10 4 11 4 12 4 , 10 1 11 1 12 1 ) и 19 20 21 (19 3 20 3 21 3 , 19 1 20 1 21 1 ).

• 3.    Определим 0-плоскость A ( А 1 , A ₂) пересечения 1-поверхностей 1 2 3 (1 1 2 1 3 1 ) и 10 11 12 (10 1 11 1 12 1 ) и 0-плоскость D ( D 1 , D ₂) пересечения 1-поверхностей 10 11 12 (10 1 11 1 12 1 ) и 19 20 21 (19 1 20 1 21 1 ).

• 4.    Присваивая компоненту x ₃ значения x ₃² и x ₃³, аналогичным образом получим 0-плоскости B ( В 1 , B ₂), L ( L 1 , L ₂) и 0-плоскости C ( С 1 , C 2 ), M ( M 1 , M 2 ) соответственно.

• 5.    Дискретное число полученных 0-плоскостей A ( А 1 , A 2 ) , B ( В 1 , B ₂) и C ( С 1 , C 2 ) образует 1-поверхность АВС ( А 1 В 1 С 1 , А ₂ В ₂ С ₂ ) , которая определяет область оптимизации компонентов х 1 , х ₂ , х 3 в зависимости от значений оптимизирующих факторов Х оптим и ф оптим . Дискретное число полученных 0-плоскостей D , L и M образует 1-поверхность DLM ( D 1 L 1 M 1 , D 2 L 2 M 2 ), которая определяет область оптимизации компонентов х 1 , х 2 , х 3 в зависимости от значений оптимизирующих факторов ф оптим и f >птим .

• 6.    Пересечение 1-поверхностей АВС ( А 1 В 1 С 1 , А 2 В 2 С 2 ) и DLM ( D 1 L 1 M 1 ,

D 2 L 2 M 2 ) определяет искомую 0-плоскость

N (N1, N2), которая является областью оптимизации компонентов х 1, х2, х3 в зависимости        от        значений оптимизирующих факторов Хоптим, фоптим и f>птим. Координаты х 1^, х 2 ^, х 3 ^  0- плоскости N  (N1,  N2)  определяют комбинацию значений компонентов, при которых Х = Хоптим, ф = φоптим и f = fоптим.

Разработанные алгоритмы приме- нимы при различном числе компонентов (технологических параметров) и оптимизирующих факторов, количество и тех, и других может увеличиваться в зависимости от требований прикладной задачи.

Действие сформулированных алгоритмов рассмотрено при построении оптимизационных моделей конкретных технологических процессов.

Для решения прикладных задач швейного производства, в частности, оптимизации процессов соединения деталей швейных изделий, разработаны алгоритмы определения области оптимизации значений основных параметров режимов соединения в зависимости от значений оптимизирующих факторов (показателей качества) [10]. С учетом требований прикладных задач сформулированы алгоритмы определения оптимальной области трех параметров процесса для двух и трех оптимизирующих факторов. При этом количество оптимизирующих факторов не ограничивается тремя, так же как и количество параметров процесса.

По результатам теоретических и экспериментальных исследований свойств соединений, выполненных на текстильных термопластичных материалах методом лазерной сварки, построены графические оптимизационные модели, апробация которых показала, что установленные по чертежам значения основных параметров режимов процесса обеспечивают получение заданной прочности сварных швов.

Этим подтверждается практическая пригодность алгоритмов определения оптимизирующей области значений параметров в зависимости от значений оптимизирующих факторов, разработанных на основе чертежа Радищева.

Универсальность вышеуказанных алгоритмов подтверждена на примере ниточного способа соединения деталей швейных изделий.

Графические оптимизационные модели позволяют, варьируя значения основных параметров процессов, выбирать режимы, обеспечивающие требуемые свойства шва, и могут быть использованы в качестве операционных карт выбора оптимальных режимов технологических процессов соединения деталей швейных изделий.

Для автоматизации процесса построения графических оптимизационных моделей создана компьютерная программа «Оптимизация процессов», позволяющая строить чертежи оптимизационных моделей и подбирать оптимальные значения основных параметров в зависимости от заданных значений нескольких оптимизирующих факторов [11].

На рис. 2 представлена блок-схема программы, реализующая алгоритмы определения оптимизирующих областей параметров в зависимости от значений оптимизирующих факторов.

Таким образом, исследование многофакторных, многокомпонентных систем методами начертательной геометрии является перспективной научной областью, а теоретические и практические результаты данной работы могут способствовать дальнейшему ее развитию. Отметим, что рассмотренные алгоритмы определения оптимальных значений многофакторных, многокомпонентных систем могут быть применимы не только в вышерассмот- ренных технологических задачах, но и, например, при синтезе новых материалов, которые будут удовлетворять некоторым оптимизирующим факторам, в решении экологических проблем и т. д.