Perturbation theory in the solution of the Schrodinger equation

Student Magistrant

Departament of «Information and computing technology» 2nd year, Faculty of «Master and Postgraduate» Povolzhsky State University of Telecommunications and Informatics Russia, Samara

Supervisor: Alishev Y.V.

Assistant professor

Departament of « Theoretical Foundations of Radio Engineering and

Communication»

Аускультация легких - выслушивание, анализ и диагностика звуков, которыми сопровождается работа лёгких. Имеет почти 200-летнюю медицинскую историю ¹ . Тем не менее, до сих пор не удавалось автоматизировать эту диагностическую процедуру, создать технологии, которые могли бы найти применение в современной медицинской практике, и переместить данную процедуру из разряда врачебного искусства в чётко детерминированный процесс.

Вдохновившись успехами нейронных сетей за последние годы, была предпринята попытка классификации дыхательных шумов с помощью многослойного персепртона.

Найти в открытом доступе набор записей дыхания человека не так-то просто, но всё же, удалось собрать и систематизировать около 50 записей, разбив их на три класса: хрипы, крепитация (потрескивания) и отсутствие дополнительных дыхательных шумов.

Отдельной подзадачей является представление данных на вход нейронной сети. Здесь имеется большое количество подходов. Можно считывать отсчёты оцифрованного сигнала окнами равной длинны, наслоенными друг на друга, чтобы не пропустить содержащийся хрип или потрескивание, при этом длинна окна подбирается так, чтобы каждое окно содержало в себе информацию о вдохе или о выдохе и не состояло полностью из отсчётов, в которых отсутствует информация о дыхании. Минус такого подхода в том, что число отсчётов может быть относительно большим и потребует ёмких вычислительных ресурсов для обучения и прямого прогона нейронной сети.

Другим вариантом представления данных является получение полного спектра сигнала. Данная характеристика не привязана ко времени и окно, содержащее в себе частотный набор, может варьироваться до относительно небольших значений. Такой подход и был использован далее.

Имея на входе записи в формате mp3 и wave , были выполнены следующие преобразования входных данных для нейронной сети:

• 1.    Чтение отсчётов из файла.

• 2.    Децимация сигнала . Исходя из анализа набора данных, рабочим частотным диапазоном был выбран отрезок до 2кГц. Поэтому

• 3.    было выполнено прореживание по частоте и брался каждый 11ый отсчёт, при том, что исходная частота дискретизации файлов – 44100 Гц.

• 4.    Разбиение отсчётов на окна определённого размера.

• 5.    Вычисление мгновенного спектра. Для каждого окна выполняется быстрое преобразование Фурье, переводя сигнал в амплитудно-частотную форму.

• 6.    Вычисление полного спектра. Полученные значения окон усредняются, в результате чего мы имеем полную амплитудночастотную характеристику сигнала.

• 7.    Нормализация данных от 0 до 1.

Результатом всех преобразований является просто массив чисел с плавающей запятой, подающийся на вход сети, и размер которого мы можем варьировать.

Теперь необходимо определиться с архитектурой нашего многослойного персептрона. Так как не существует точного подхода позволяющего однозначно сказать сколько необходимо нейронов в слое и самих слоев для успешной классификации, были рассмотрены следующие эвристические подходы: снизу вверх и сверху вниз. Первый подход подразумевает постепенное добавление слоёв и нейронов до достижения заданного качества классификации. Второй подход напротив, выбирается максимально допустимое вычислительными ресурсами число слоёв и нейронов и уменьшается до достижения минимального порога качества классификации.

С количеством скрытых слоёв и нейронов в них мы разобрались, осталось определить количество входных и выходных нейронов. Количество выходных нейронов будет равно трём – по нейрону на каждый класс, а с входными сложнее. Их число будет подбираться эвристически, так же как и число скрытых слоёв. Минимальным числом входов нейронной сети будет минимальное число необходимых признаков для обучения сети.

В качестве функции активации для скрытых и выходных слоёв была использована сигмоидальная функция, а в качестве метода обучения – алгоритм обратного распространения ошибки.

В ходе экспериментов была получена наилучшая конфигурация сети изображенная на рисунке 1. Где N – составило 64 отсчёта. Постепенное уменьшение числа нейронов в скрытых слоях способствует обобщению информации и повышению уровню абстракции на скрытых слоях сети.

Обучение сети проводилось на 30-ти записях, по 10 записей на каждый класс, и тестировалось на 15-ти записях, по 5 на каждый класс. Чтобы компенсировать небольшое количество данных для обучения и тестирования, тестовые и обучающие данные менялись и прогонялись неоднократно, чтобы получить среднюю статистику. В итоге процент успешно классифицированных образцов составил 59 ± 3%.

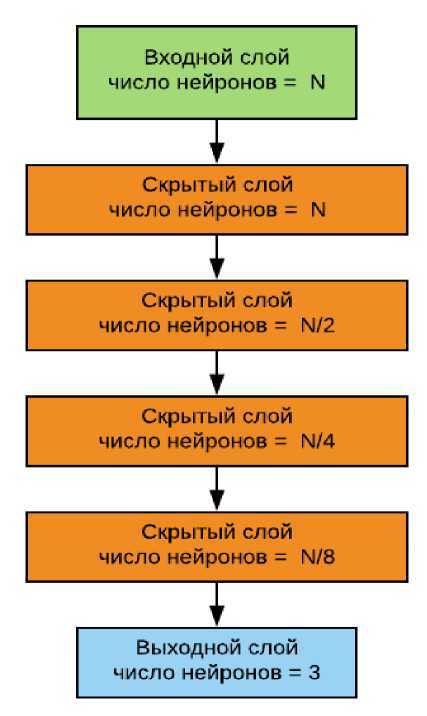
Рисунок 1 – конфигурация многослойного персептрона, где N – число входных данных

Результат скромный и даже неуместный, если речь идёт о медицине, но может быть улучшен за счёт увеличения обучающей выборки, за счёт иного представления входных данных и применения других топологий нейронных сетей.