Первые звуковые точки в каналах

Дозвуковые течения, в каждой точке которых местное число Маха М 6 1, и при этом хотя бы в одной точке число Маха, достигает единицы, называются критическими течениями. В задачах обтекания они соответствуют критическому числу Маха М* набегающего

«Московский физико-технический институт (национальный исследовательский университет)», 2021

потока, разграничивающему чисто дозвуковые течения и обтекания с местными сверхзвуковыми зонами. Если в набегающем потоке число Маха М _ю >  М*, то при обтекании тела возникают местные сверхзвуковые зоны, что может привести к возникновению скачков уплотнения, которые, в свою очередв, могут вызывать отрыв потока. И скачки, и отрыв резко увеличивают сопротивление. Поэтому практически важной является задача мак-спмпзащш М* — построение форм обтекаемых тел с максимальным значением М* (при заданных изопериметрических условиях).

Известен эмпирический факт, что при медленном повышении дозвуковой скорости набегающего потока первые звуковые точки, в которых местное число Маха М = 1, появляются именно на поверхности обтекаемого тела [1]. Из этого эмпирического факта возникло предположение: предполагается, что среди первых звуковых точек обязательно есть точки, которые расположены на поверхности обтекаемого тела. Поэтому при поиске М*, для разных чисел Маха набегающего потока выясняют наличие звуковых точек не во всех точках течения, а только на поверхности обтекаемого тела. Это существенно упрощает решение задач максимизации М* [2-8]. Однако существуют и случаи расположения первых звуковых точек внутри течения. Например, в задаче о звуковой струе. Это режим истечения дозвукового потока из сужающегося сопла в пространство с пониженным давлением, сопровождающееся дополнительным разгоном потока до скорости звука, при котором однородный звуковой поток (звуковая струя) образуется на конечном расстоянии от среза сопла и следует за прямой звуковой линией перпендикулярно ей [9]. Пример звуковой струи не противоречит предположению о том, что первые звуковые точки возникают именно на поверхности обтекаемого тела. Дело в том, что в задаче о звуковой струе нет обтекаемых тел. Пример звуковой струи приведён для того, чтобы показать содержательность вопроса о месте расположения звуковых точек в критическом течении.

Теоретические исследования этого вопроса были проведены в работе [2], где было получено необходимое условие существования внутренних звуковых точек в течениях с М 6 1 (т.е. в критических течениях). Ниже это необходимое условие будет называться теоремой о звуковой точке. Согласно этой теореме, если в дозвуковом стационарном безвихревом баротропном течении существует внутренняя звуковая точка (М = 1), то она лежит на звуковой плоскости, которая в каждой точке перпендикулярна скорости газа и не может заканчиваться внутри течения. В работе [2] на основе теоремы о звуковой точке был сделан вывод о месте расположения первых звуковых точек только на поверхности летательных аппаратов выпуклой формы. Таким образом, при максимизации М* в работах [2-8] использовался не только эмпирический, но и теоретически обоснованный факт появления первых звуковых точек именно на поверхности обтекаемого тела.

Заметим, что факт расположения первых звуковых точек на поверхности обтекаемых тел можно попытаться получить из дозвукового принципа максимума [10]. Согласно этому принципу, максимум модуля скорости в дозвуковых безвихревых течениях баротропного газа достигается на границе течения. Соответствующее доказательство для полных уравнений Эйлера можно найти в [11, гл. II]. Это доказательство существенным образом опирается на условие М < 1, которое должно быть выполнено во всех точках, и поэтому неприменимо к критическим течениям. Однако при дополнительном предположении, что картина стационарного течения (решение краевой задачи для уравнений Эйлера) непрерывно зависит от числа Маха набегающего потока, из дозвукового принципа максимума следует, что среди звуковых точек в критическом течении обязательно будут точки на границе течения (на обтекаемой поверхности). Но утверждение о том, что картина стационарного течения непрерывно зависит от числа Маха набегающего потока, в настоящее время не имеет теоретического обоснования. Поэтому предложенное объяснение, основанное на дозвуковом принципе максимума, не является теоретически обоснованным.

Как сказано выше, теорема о звуковой точке позволила сделать вывод о месте появления первых звуковых точек на обтекаемой поверхности только для выпуклых тел. В данной работе обнаружено ещё одно условие на относительное расположение обтекаемого тела и звуковой плоскости. В резулвтате предложен простой способ проверки тел с более сложными поверхностями на возможноств появления первых звуковых точек внутри течения (не на поверхности тел).

2.    Пример применения теоремы о звуковой точке

Простейшим течением со звуковой поверхноствю является прямолинейный однородный поток газа, движущийся со скороствю звука. Нетривиальное течение с плоской звуковой поверхностью - звуковая струя [8]. Однако во многих случаях можно показать, что такая плоскость не может существовать. И, как следствие, первые звуковые точки располагаются только на поверхности тел. Например, при обтекании выпуклого тела любая плоскость, проходящая через внутреннюю точку течения, простирается в бесконечность. Поскольку во всем течении М 6 1, а в набегающем потоке М^ < 1, то существование звуковой плоскости невозможно вследствие условия затухания возмущений. Поэтому звуковые точки и в этих случаях могут находиться только на поверхности. (Это рассуждение заимствовано в [2].)

Рассмотрим теперь (невыпуклое) обтекаемое тело с углублением, в которое можно поместить плоскую поверхность, не простирающуюся в бесконечность. Поэтому нельзя воспользоваться противоречием с условием М _ю<  1. Но если эта поверхность будет звуковой, то в углубление должен будет втекать (или вытекать) газ со скоростью звука. Это противоречит закону сохранения массы, если только углубление не является началом сквозного отверстия (канала) или, например, входным отверстием воздухозаборника. В общем случае закону сохранения массы будет противоречить расположение звуковой плоскости в любых углублениях поверхности односвязных областей. И получается, что звуковые точки могут находиться только на поверхности таких тел. (Это рассуждение также заимствовано в [2].)

Как замечено выше, теорема о звуковой точке вместе с законом сохранения массы не позволяют рассмотреть случай течения в канале. Оказывается, что для широкого класса каналов первые звуковые точки также будут возникать только на стенках каналов. Этому посвящён следующий раздел.

3.    Геометрическое требование

Скорость невязкого газа направлена по касательной к обтекаемым поверхностям. Это накладывает геометрическое требование: нормаль к звуковой плоскости ст должна быть касательным вектором к обтекаемым поверхностям во всех точках их пересечения с плоскостью ст. (Несмотря на простоту этого утверждения, в доступной автору литературе оно не упоминается, и представляет собой основной результат настоящей статьи.)

В некоторых случаях существует плоская поверхность, которая удовлетворяет геометрическому требованию, закону сохранения массы и не противоречит условию М ^ <  1 (в этих случаях обнаруженное в данной статье геометрическое требование оказывается бесполезным). Например, самое узкое сечение сопла Лаваля. Целое семейство таких поверхностей можно указать для цилиндра с открытыми торцами - это плоские поверхности внутри цилиндра, перпендикулярные его стенкам. Одна поверхность существует для тора - это «перепонка» на самой узкой части отверстия тора.

Применительно к подобным телам из теоремы о звуковой плоскости не следует, что соответствующие течения со звуковыми плоскостями могут быть реализованы. Например, «перепонку» на самой узкой части отверстия тора не следует воспринимать, как звуковую плоскую поверхность, соответствующую какому-либо критическому течению. Это всего лишь вариант возможного расположения звуковой плоскости, не противоречащий теореме о звуковой точке, геометрическому требованию, закону сохранения массы и условию Мго < 1. Эти условия всего лишь необходимые условия, предъявляемые к звуковой плоскости. Возможность реализации этого варианта должна исследоваться с помощью других теорем аэродинамики, что выходит за рамки настоящей статьи.

Однако для большинства тел сложной формы плоскую поверхность, удовлетворяющую геометрическому требованию, невозможно подобрать, и можно сделать вывод, что первые звуковые точки могут находиться только на их поверхности. Речь идёт прежде всего о течениях в каналах. В частности, такую поверхность невозможно подобрать для осесимметричного канала (стенки - поверхности вращения вокруг оси симметрии), если радиус канала монотонно изменяется вдоль оси. Поэтому первые звуковые точки могут находиться только на стенках канала. Один только этот пример показывает, что геометрическое требование, обнаруженное в настоящей статье, является действенным дополнением к теореме о звуковой точке при исследовании возможности существования внутренних звуковых точек и возникновения первых звуковых точек на поверхности.

В каждом конкретном случае проверка существования плоской поверхности, удовлетворяющей геометрическому требованию, представляет гораздо более простую задачу, чем расчёт или эксперимент. Приведём два примера.

Рассмотрим канал, представленный на рис. 1. Штрихованные отрезки соответствуют сечениям, которые ортогональны к обеим стенкам. На таких отрезках возможность появления первых звуковых точек внутри течения не противоречит геометрическому требованию, и требует исследований, выходящих за рамки статьи. В других местах никакие отрезки не образуют одновременно прямые углы с обеими стенками, поэтому в них не могут появляться первые внутренние звуковые точки.

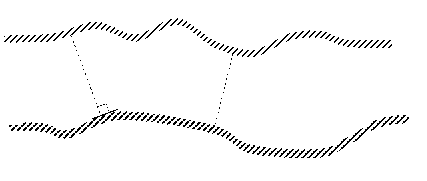
Рис. 1

Другой пример - строго монотонно расширяющаяся труба (рис. 2). Очевидно, что не существует плоскости, нормальной к поверхности трубы во всех точках пересечения этой плоскости с поверхностью трубы. Поэтому первые звуковые точки могут возникать только на стенках (при любом направлении течения).

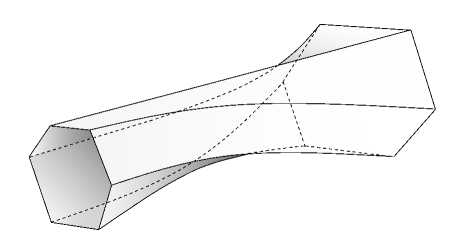
Рис. 2

Замечание. В околозвуковых течениях звуковые поверхности отделяют дозвуковые зоны от сверхзвуковых и эти звуковые поверхности не всегда примыкают к обтекаемым поверхностям под прямым углом. Если говорить о результатах (об углах примыкания), полученных в итоге строгих исследований уравнений Эйлера, то их можно найти в [12].

4.    Заключение

Рассмотрены баротропные безвихревые стационарные течения с числом Маха М 6 1. Условие М 6 1 соответствует появлению первых звуковых точек при медленном повыше- нии скорости набегающего потока. Для проверки возможности появления первых звуковых точек внутри течения предложено использовать (наряду с известной теоремой о звуковой точке) геометрическое требование, состоящее в том, что нормаль к звуковой плоскости ст должна быть касательным вектором к обтекаемым поверхностям во всех точках их пересечения с плоскостью ст. Приведён пример неизвестного ранее утверждения, полученного с использованием геометрического требования (о месте первых звуковых точек в каналах с переменным радиусом).

Результаты могут быть применены для качественного анализа течений, а также при построении пространственных конфигураций каналов с максимальным критическим числом Маха.