Первый российский опыт клинической апробации алгоритма Темплтона в условиях центра вспомогательных репродуктивных технологий

Результативность лечения бесплодия с помощью вспомогательных репродуктивных технологий (ВРТ) до настоящего времени остается недостаточно высокой [1]. Данное обстоятельство диктует необходимость поиска модифицируемых факторов, влияющих на результативность программ ВРТ, а также возможностей прогнозировать исход лечения на преконцептивном этапе.

Математическая модель Темплтона [7], разработанная в Великобритании в 1996 году, в различных модификациях до настоящего времени используется за рубежом для прогнозирования результативности метода экстракорпорального оплодотворения и переноса эмбриона в полость матки (ЭКО и ПЭ). Согласно данным Smeenk [6], Leushuis [3], van Loendersloot, Arvis, оригинальный алгоритм Темплтона при внешней оценке в современных условиях демонстрирует умерен-

ную прогностическую мощность, однако может быть легко адаптирован к условиям конкретного центра ВРТ [2, 3, 4. 6]. Несомненным преимуществом данного прогностического алгоритма является использование в качестве основы принятия решений наиболее доступных анамнестических и клинических данных. Возможность объективной стратификации риска неудачного исхода программы ЭКО и ПЭ на этапе первичной консультации супружеской пары объясняет актуальность использования алгоритма Темплтона и в отечественной медицинской практике.

Цель исследования: оценить возможность использования модели Темплтона для прогнозирования результативности метода ЭКО и ПЭ в условиях современного российского центра вспомогательных репродуктивных технологий.

Материалы и методы. В проспективном исследовании участвовали 348 супружеских пар, проходивших лечение бесплодия с помощью метода ЭКО и ПЭ в ГБУЗ «Самарский областной центр планирования семьи и репродукции» в 2013 году. Критериями исключения являлись отсутствие информированного добровольного согласия на участие в исследовании, использование в протоколе ЭКО и ПЭ гамет донора, отсутствие данных об исходе индуцированной беременности. Регистрационная карта супружеской пары в случае родов завершалась при достижении ребенком возраста 1 месяца.

Реализация протоколов ЭКО и ПЭ соответствовала действующим стандартам. Индивидуальная вероятность наступления беременности и рождения ребенка в результате ЭКО и ПЭ определялась с помощью прогностического уравнения Темплтона и сопоставлялась с фактическим результатом лечения. Модель Темплтона является уравнением логистической регрессии, бинарной зависимой переменной (P) в котором выступает исход программы ЭКО и ПЭ:

P =

1 + e " y

, где y = -2,028 + 0,00551x (A -16)2 - 0,00028x (A -16)3 + i - 0,069 x(B)-- 0,0711x(C)+0,7587x(D)+0,2986x(E)+0,2277x( F)+ 0,1117x( G)

В представленном алгоритме используются следующие клинические параметры: возраст пациентки (A), длительность бесплодия (i = 0,2163 в случае 1-3 лет, i = -0,0839 в случае 4-9 лет, i = -0,1036 в случае 7-12 лет, i = -0,4179 в случае более 13 лет бесплодия), число безуспешных попыток ЭКО и ПЭ в анамнезе (B), наличие трубного фактора бесплодия (С), рождение живого ребенка в результате ЭКО и ПЭ в анамнезе (D), беременность в результате ЭКО и ПЭ в анамнезе, не закончившаяся родами (E), рождение живого ребенка в результате самопроизвольной беременности в анамнезе (F), самопроизвольная беременность в анамнезе, не закончившаяся родами (G). Параметры C, D, E, F, G являются бинарными качественными переменными, принимающими значение 0 и 1 в случае отсутствия и наличия клинического фактора, соответственно. Согласно предложению Smeenk, в представленном алгоритме параметры A и i могут быть модифицированы: используются показатели возраста пациентки и длительности бесплодия, регистрировавшиеся при первой попытке ЭКО и ПЭ [6]. В качестве градаций зависимой переменной P могут выступать следующие пары качественных признаков: «рождение живого ребенка» и «попытка ЭКО и ПЭ не завершилась рождением живого ребенка», «клиническая беременность» и «отсутствие клинической беременности в результате данной попытки». Модель Темплтона создавалась для прогноза живорождения, однако некоторые авторы при апробации данной модели в качестве исхода лечения предлагают рассматривать клиническую беременность [3]. В нашем исследовании использованы оба варианта представления зависимой переменной как для оригинального алгоритма Темплтона, так и для модификации Smeenk. Прогностическая значимость изучаемой модели определялась нами на основании показателей дискриминационной и калибрационной адекватности последней. Дискриминационная адекватность прогностического инструмента – способность дифференцировать положительный и отрицательный исход изучаемого явления – оценивалась с помощью ROC-анализа. Калибрационная адекватность модели – соответствие предсказанной вероятности изучаемого исхода и его фактической частоты – оценивалась согласно методу Cox, детализированному Miller [5]. Статистический анализ данных и их моделирование выполняли в среде пакета SPSS 21. Описательные статистики представлены в виде среднего и стандартного отклонения среднего (M±SD), минимального и максимального значений (min и max) для количественных признаков, абсолютного числа наблюдений и доли наблюдений в процентах для качественных признаков. Расчет вероятности успешного исхода программы ЭКО и ПЭ согласно алгоритму Темплтона и его модификациям осуществляли с помощью командного синтаксиса SPSS. Критическое значение уровня статистической значимости принимали равным 0,05.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ИХ ОБСУЖДЕНИЕ

Характеристика участников исследования согласно данным анамнеза представлена в таблице 1. В подавляющем большинстве наблюдений показанием для реализации программы ЭКО и ПЭ в исследуемой группе являлось сочетание нескольких факторов бесплодия. В 66,1% наблюдений (230/348) были выявлены не соответствующие референтным показатели спермограммы, в 51,7% наблюдений (180/348) диагностировалось наличие трубно-перитонеального фактора женского бесплодия. Несколько уступали перечисленным по частоте встречаемости следующие факторы: ановуляторное бесплодие (34,5%, 120/348), эндометриоз (33,6%, 117/348), снижение овариального резерва (28,2%, 98/348), наличие совпадений более двух локусов системы HLA в супружеской паре (18,1%, 63/348), наличие полиморфизмов генов системы гемостаза (25,3%, 88/348). У 22,9% пациенток (80/348) была диагностирована миома матки малых размеров, в 18,4% наблюдений (64/348) протоколу ЭКО и ПЭ предшествовал курс комплексной терапии гистологически подтвержденного хронического эндометрита. Среди хронических экстрагенитальных заболеваний, требующих постоянной медикаментозной коррекции, наиболее часто выявлялся хронический аутоиммунный тиреоидит (5,5% наблюдений, 19/348).

Во всех исследуемых случаях реализация протокола ЭКО и ПЭ соответствовала действующим стандартам. В 80,2% наблюдений (279/348) стимуляция суперовуляции проводилась по короткому протоколу с антагонистами гонадо-либерина (антГнРГ), в 15,2% наблюдений (53/348) использовался длинный протокол с агонистами

Таблица 1. Репродуктивный анамнез участников исследования

Характеристика супружеской пары M±SD min max Возраст пациентки 33,32±4,20 22 43 Возраст пациентки при первой попытке ЭКО и ПЭ 32,35±4,11 22 41 Возраст супруга 35,55±5,16 25 53 Длительность бесплодия 6,75±4,54 1 22 Длительность бесплодия при первой попытке ЭКО и ПЭ 6,33±4,23 1 22 Число неудачных попыток ЭКО и ПЭ 0,75±1,11 0 9 Абсолютное число наблюдений Доля наблюдений, % Рождение живого ребенка в результате ЭКО и ПЭ в анамнезе 12 3,4 Беременность в результате ЭКО и ПЭ, не закончившаяся рождением живого ребенка 32 9,2 Рождение живого ребенка в результате самопроизвольной беременности в анамнезе 45 12,9 Самопроизвольная беременность в анамнезе, не закончившаяся рождением живого ребенка 146 42 гонадолиберина (аГнРГ). Принимая во внимание наличие снижения овариального резерва, в трех случаях был реализован протокол минимальной стимуляции суперовуляции. В 13 наблюдениях (3,7%) стимуляция суперовуляции не проводилась в связи с запланированным трансфером криоконсервированных эмбрионов. Оплодотворение ооцитов, полученных при трансвагинальной пункции фолликулов, в 50,3% наблюдений (175/348) производилось по стандартной методике ЭКО, в 44,5% наблюдений (155/348) была реализована методика ИКСИ.

Исходы программ ЭКО и ПЭ в исследуемой группе представлены в таблице 2.

На втором этапе исследования сопоставление реальных и предсказанных результатов программы ЭКО и ПЭ позволило оценить дискриминационную и калибрационную адекватность алгоритма Темплтона и его модификаций. Результаты ROC-анализа изучаемых алгоритмов представлены в таблице 3. Качество прогностического алгоритма оценивается согласно показателю площади под ROC-кривой (AUC), принимающему значения от 0,5 до 1.

Согласно таблице 3, наилучший результат оценки дискриминационной адекватности демонстрирует оригинальный алгоритм Темплтона: значение AUC, равное 0,61, свидетельствует об удовлетворительном качестве прогностического инструмента. ROC-кривая для данного алгоритма представлена на рисунке 1.

Оптимальная точка отсечения для представленного алгоритма, определенная согласно максимальному значению полусуммы чувствительности и специфичности, соответствовала 0,13. Показатели чувствительности и специфичности прогностической модели в данной точке отсечения составили 56% и 60%, соответственно.

Следует отметить, что доверительные интервалы показателей AUC для всех представленных в таблице 3 алгоритмов включают значения диапазона 0,5-0,6, соответствующего неудовлет-

Таблица 2. Исход программ ЭКО и ПЭ в исследуемой группе

Исход программы ЭКО и ПЭ	Абсолютное число наблюдений	Доля наблюдений, %
Ооциты не получены	18	5,2
Отсутствие оплодотворения ооцитов	8	2,3
Другая причина отмены переноса эмбрионов в полость матки	4	1,1
Отсутствие беременности	151	43,4
Потеря беременности до 12 недель	40	11,5
Потеря беременности после 12 недель	5	1,4
Рождение живого ребенка	122	35,1
Итого	348	100

Таблица 3. Дискриминационная адекватность оригинального алгоритма Темплтона и модификации Smeenk для различных вариантов представления зависимой переменной

Прогностический алгоритм	AUC	SE	95% доверительный интервал AUC	р
Оценка вероятности наступления беременности, алгоритм Темплтона	0,57	0,031	0,51–0,63	0,032
Оценка вероятности живорождения, алгоритм Темплтона	0,61	0,031	0,55–0,67	0,001
Оценка вероятности наступления беременности, алгоритм Темплтона в модификации Smeenk	0,56	0,031	0,50–0,62	0,071
Оценка вероятности живорождения, алгоритм Темплтона в модификации Smeenk	0,59	0,032	0,53–0,65	0,006

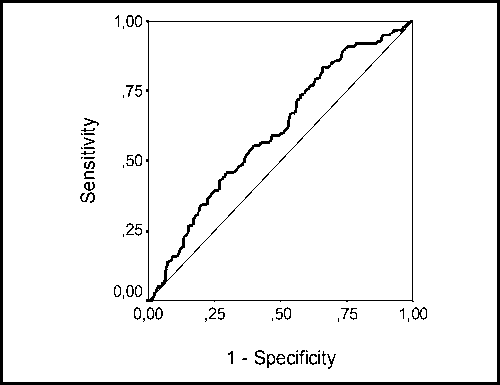
Рис. 1 . ROC-анализ оригинального алгоритма Темплтона для прогнозирования рождения живого ребенка в результате ЭКО и ПЭ

ворительному качеству прогностической модели. Полученные результаты также доказывают нецелесообразность использования алгоритма Темплтона в модификации Smeenk для оценки вероятности наступления беременности: значение уровня статистической значимости p, равное 0,071, не позволяет отвергнуть нулевую гипотезу о равенстве значения показателя AUC 0,5. Таким образом, наиболее предпочтительным является использование оригинального алгоритма Темплтона для оценки вероятности рождения живого ребенка в результате ЭКО и ПЭ. Значение вычисленной согласно данному алгоритму вероятности живорождения, не превышающее 0,13, может служить основанием для включения пациентов в группу риска неудачного исхода программы ЭКО и ПЭ. При интерпретации полученных результатов следует принимать во внимание невысокую, но удовлетворительную дискриминационную адекватность используемого алгоритма.

Оценка соответствия реальных и предсказанных исходов программы ЭКО и ПЭ (калибрационная адекватность) проводилась согласно методу Cox, детализированному Miller: качество про- гностического инструмента интерпретируется согласно коэффициентам линейных регрессионных моделей зависимости наблюдаемой частоты успешного исхода программы от предсказанной. В случае идеальной калибрационной способности модели константа регрессионного уравнения (свободный член а, соответствует подъему графика в точке х=0 относительно оси абсцисс) равна нулю, тогда как угловой коэффициент наклона линии регрессии (коэффициент b, соответствует тангенсу угла наклона графика к оси абсцисс) равен единице. При графическом изображении в данном случае линия регрессии совпадает с биссектрисой первого координатного угла. Значения a>0 свидетельствуют о систематическом занижении прогнозируемой вероятности исследуемого исхода, при a<0 имеет место завышение прогнозируемых вероятностей. Значения b, отличные от 1, свидетельствуют о диспропорциональном завышении/занижении прогнозируемых вероятностей изучаемого исхода.

Данные оценки калибрационной адекватности алгоритма Темплтона и его модификаций по Smeenk в случае прогнозирования наступления

Таблица 4. Коэффициенты линейных регрессионных моделей зависимости наблюдаемой частоты наступления беременности от предсказанной вероятности, вычисленной согласно прогностическим алгоритмам Темплтона и модификации Smeenk

Алгоритм прогноза	Интервализация вычисленных вероятностей	Коэффициент уравнения линейной регрессии	Значение коэффициента	SE	p
Templeton	децили	a	0,44	0,07	<0,001
		b	0,99	0,52	0,092
Templeton	квинтили	a	0,40	0,06	0,008
		b	1,31	0,45	0,060
Модификация	децили	a	0,45	0,08	0,001
Smeenk		b	0,86	0,58	0,180
Модификация	квинтили	a	0,43	0,05	0,004
Smeenk		b	0,97	0,38	0,081

1,00

0,90

0,80

0,70

0,60

0,50

0,40

0,30

0,20

0,10

0,00

0,00

0,20      0,40      0,60

Рассчитанная вероятность

0,80       1,00

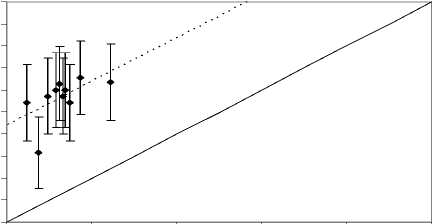
Рис. 2. Калибрационный график. Зависимость наблюдаемой частоты наступления беременности от предсказанной согласно алгоритму Темплтона: линейная регрессионная модель, интервализация вычисленных вероятностей по децилям

беременности в результате ЭКО и ПЭ представлены в таблице 4.

Уровни статистической значимости p, представленные в таблице 4, являются результатом проверки нулевой гипотезы о равенстве коэффициентов линейных регрессионных уравнений нулю. Согласно полученным результатам, каждый из представленных алгоритмов демонстрирует относительно пропорциональное занижение вероятностей наступления беременности в результате ЭКО и ПЭ на 40-44%. Рисунок 2 наглядно демонстрирует выявленную тенденцию.

Данные оценки калибрационной способности модели Темплтона и ее модификации по Smeenk в случае прогнозирования рождения живого ребенка представлены в таблице 5.

Таблица 5 . Коэффициенты линейных регрессионных моделей зависимости наблюдаемой частоты рождения живого ребенка от предсказанной вероятности согласно прогностическим алгоритмам Темплтона и модификации Smeenk

Алгоритм прогноза	Интервализация вычисленных вероятностей	Коэффициент уравнения линейной регрессии	Значение коэффициента	SE	p
Templeton	децили	a	0,13	0,06	0,074
		b	1,70	0,46	0,006
Templeton	квинтили	a	0,11	0,08	0,275
		b	1,89	0,59	0,048
Модификация	децили	a	0,16	0,08	0,102
Smeenk		b	1,43	0,58	0,040
Модификация	квинтили	a	0,13	0,10	0,300
Smeenk		b	1,63	0,72	0,109

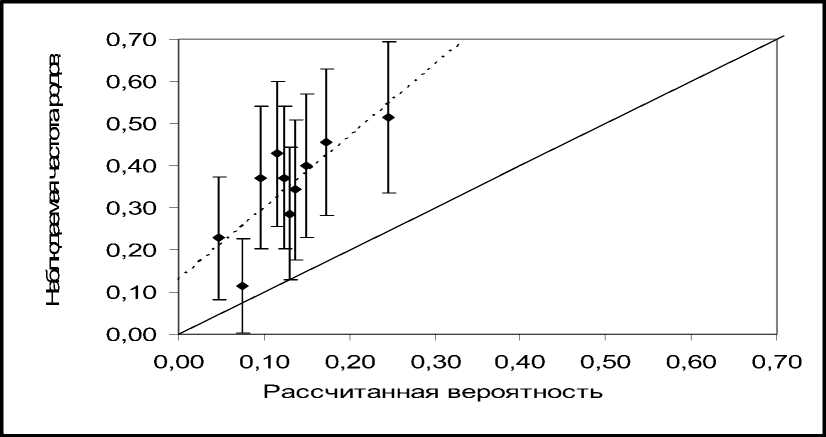
Рис. 3. Калибрационный график. Зависимость наблюдаемой частоты рождения живого ребенка от предсказанной согласно алгоритму Темплтона: линейная регрессионная модель, интервализация вычисленных вероятностей по децилям

Согласно данным таблицы 5, наибольшее приближение к референтным показателям калибрационной способности выявлено при оценке алгоритма Темплтона без модификации с интер-вализацией по децилям. Однако в данном случае, как демонстрирует рисунок 3, отмечается диспропорциональное (b>1) занижение предсказываемых вероятностей рождения живого ребенка.

Полученные данные свидетельствуют о том, что алгоритм Темплтона приемлемо работает в области плохого прогноза (в случае предсказанной вероятности рождения живого ребенка менее 10%) и существенно занижает вероятность удачи при более высоких оценках. Так, в нашем исследовании у 70 пациенток с предсказанной вероятностью удачи менее 10% лишь в 17% наблюдений (12/70) индуцированная в результате ЭКО и ПЭ беременность закончилась рождением живого ребенка. Напротив, в группе из 33 пациенток с ожидаемой высокой вероятностью благоприятного исхода программы ЭКО и ПЭ (вероятность родов более 20%) рождение живых детей регистрировалось лишь в 17 наблюдениях (52%). Полученные результаты согласуются с данными оценки дискриминационной адекватности изучаемых алгоритмов: предпочтительным является использование оригинальной модели Темплтона для прогнозирования рождения живого ребенка в результате ЭКО и ПЭ, наиболее достоверные результаты следует ожидать в диапазоне предсказанных вероятностей менее 13%.

ЗАКЛЮЧЕНИЕ

Математическая модель Темплтона, созданная в 1996 году в Великобритании на основании многофакторного анализа данных свыше 52000 циклов ЭКО и ПЭ, является результатом исследования, непревзойденного по охвату наблюдений, и представляет в настоящее время не только исторический, но и практический интерес. Прогностический алгоритм, основанный на данных возраста и репродуктивного анамнеза пациентки, может использоваться как для первичной стратификации риска неблагоприятного исхода программы ЭКО и ПЭ, так и в качестве базиса для создания новых математических моделей, отвечающих современным условиям реализации вспомогательных репродуктивных технологий.