П.Г. Кузнецов и потоки энергии в пространстве структуры (по материалам доклада на конференции "Международные научно-философские чтения имени Побиска Георгиевича Кузнецова", РАН, 25.10.2019 г.)

Принцип сохранения мощности

«Я хочу заметить, что принцип сохранения мощности, весьма отличается от других законов сохранения. Если мощность, как поток энергии – сохраняется, то его невозможно ни увеличить, ни уменьшить!!! Тем не менее, мы имеем многочисленные примеры, где имеет место усиление мощности», писал П.Г. Кузнецов [1, с. 70].

Кузнецов подчеркивал, что существует закон сохранения мощности, который он называет принципом, но для развития жизни важно усиление мощности. Если живые системы не увеличивают доступную для использования свободную энергию, не усиливают мощность, то они не могут существовать, а, тем более, развиваться, увеличивать занимаемое пространство. Что же является источником энергии, которую получает и применяет органическая жизнь для своего существования, увеличения и развития?

Жизнь на Земле обеспечивают потоки солнечной энергии

Из письма П.Г. Кузнецова академику АН СССР А.И. Опарину от 25 октября 1956 г. «Позавчера мною получено письмо, подписанное Вами. В нем сообщается, что только 10–13 части излучения Солнца приходится на биологические явления. Нет сомнения, что это очень небольшая часть солнечного излучения. Однако было время, когда и эта часть излучения рассеивалась в пространстве, а теперь обуславливает существование органической жизни на Земле» [3]. Кузнецов подчеркивает, что часть потока солнечной энергии, которая обеспечивает биологические явления, с течением времени непрерывно возрастает.

Законы сохранения и законы развития

• •    Законы сохранения определяют свойства замкнутых систем, соответствующие свойствам пространства.

• •    Законы развития должны определять свойства открытых систем, находящихся в устойчивом неравновесии.

П.Г. Кузнецов и Г. Крон

П.Г. Кузнецов рассматривал экономику как крупномасштабную систему, которой можно управлять. Для управления нужно рассматривать уровни иерархии с обменом потоками информации между ними. Оказалось, что нет математики для описания сети иерархии уровней управления.

Гелий Николаевич Поваров, один из пионеров советской кибернетики, указал Побиску Георгиевичу Кузнецову на работы американского инженера Габриэля Крона, который рассматривал сети, матрицы и тензоры. В зависимости от сложности проблемы, сложности моделируемой системы, рассматривались иерархически организованные компаунд тензоры, мульти тензоры. Метод диакоптики обеспечивает разделение сложной системы на части, и расчет по частям. Этот метод обеспечивает иерархию расчетов на разных уровнях.

Крон рассмотрел сетевые модели сложных технических и физических систем, а затем исследовал поведение многомерных, полиэдральных систем, в которых протекают процессы в виде электромагнитных волн. Полиэдральная сеть при некоторых условиях проявляет свойства самоорганизации, однако эти опубликованные результаты Крона не воспроизведены. Попытки расчета многомерной сети делал Дж. Линн [10].

Цель управления крупномасштабной системой

Князь Шэ спросил, что значит управление государством. Учитель ответил:

— Это когда радуются те, что близко. И приходят те, что далеко (Конфуций) .

Потоки энергии в работах Крона

Крон исследовал структуру связей сложных систем и потоки энергии в элементах систем. Сетевые модели единым методом представляют потоки процессов и структуру связей систем. В основе метода Крона дискретное пространство структуры. Оно отличатся от непрерывного, однородного, изотропного пространства геометрии.

Технические, физические и биологические системы рассматриваются как проекции тензора – обобщенной системы, в которой процессы, как воздействия и отклики, рассматриваются в пространстве структуры связанных элементов.

Законы сохранения и законы развития

Законы сохранения выполняются для замкнутых систем.

Для открытых систем должны существовать и выполняться законы развития.

Один из них – второй закон термодинамики, по которому все системы развиваются в направлении уменьшения свободной энергии.

Противоположным ему является закон развития жизни, по которому в ходе эволюции возрастает свободная энергия совокупности живых систем.

Пространство структуры дискретно

Пространство структуры сети дискретно, оно существует только вдоль ветвей, т.е. выделенных линий и их границ.

По этой причине свойства пространства сети отличаются от свойств обычного пространства декартовой или римановой геометрии.

Большую роль в пространстве-структуре сетей играет двойственность основных понятий: открытых и замкнутых путей, данной и двойственной сети, внешних и внутренних воздействий.

Замкнутые и открытые пути движения в пространстве

Любое движение состоит из поступательного движения (переноса) и вращательного движения.

Вращение и перенос не зависят друг от друга, и дополняют друг друга. Это два различных качества движения.

• •    Пути в пространстве могут быть или замкнутые или разомкнутые. Вращению

соответствуют замкнутые пути, переносу – открытые пути.

• •    Длина в пространстве измеряется вдоль открытых путей. Время измеряется по движению вдоль замкнутых путей.

• •    Системы могут и взаимодействовать, и не взаимодействовать с другими системами в окружающем пространстве.

• •    Потоки энергии от внутренних источников протекают в замкнутых путях. Потоки

энергии от внешних источников протекают в разомкнутых путях.

Пространство и законы сохранения

Пространство непрерывно, однородно, изотропно. Теорема Э. Нетер связывает свойства пространства и законы сохранения. Сохранение импульса выводится из однородности пространства. Сохранение момента импульса выводится из изотропности пространства. Сохранение энергии является следствием симметрии времени относительно начала отсчета. Л. Ландау [2] выводит законы сохранения из принципа наименьшего действия, не используя теорему Э. Нетер [11].

Например, закон сохранения энергии получается из уравнений движения в предположении однородности времени. Однородность времени означает, что функция Лагранжа замкнутой системы не зависит явно от времени. Поэтому производная от функции Лагранжа по времени получается как дифференцирование сложной функции.

=∑ ^ ̇+ ∑ dt 2-i dqt ̇ + ∑ ̇ ; ̈ ii приводя производную по времени к нулю:

d /\- . 9L \„ dt (∑ ̇ldq ̇ ; -L)=0

получаем, что величина, которая называется энергией:

∑

̇

-

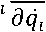
L =

не меняется при движении замкнутой системы, т.е. остается постоянной, сохраняется.

Аналогично из уравнений движения получаются закон сохранения импульса (в предположении однородности пространства) и закон сохранения момента импульса (в предположении изотропии пространства).

Пространство структуры

Пространство структуры дискретное – существует в пределах элементов (ветвей), неоднородное, неизотропное.

Координаты в пространстве структуры – это пути, линии вдоль элементов. Путь определяет набор ветвей, через которые он проходит, с учетом ориентации. Путь может выражаться через другие пути комбинированием соответствующих ветвей. Набор путей, которые не выражаются через другие пути, составляет базис пространства структуры.

Замкнутые и разомкнутые пути образуют в пространстве сети два ортогональных подпространства, которые дополняют друг друга до полного пространства.

Замкнутые пути выражаются через замкнутые пути и разомкнутые пути. Разомкнутые пути не выражаются через замкнутые пути. Замыкание пути в контур охватывает двумерную поверхность, т.е. замыкание «добавляет» новое измерение пространства. Аналогичная ситуация возникает для двумерных путей, проходящих через грани. Замкнутый двумерный путь возникает, когда грани охватят трехмерный объем, т.е. «добавляет» новое измерение пространства.

При изменении структуры соединение и разделение границ замыкает и размыкает пути. При этом меняется размерность подпространств путей в сети.

Тензорный анализ в пространстве структуры отличается тем, что пространство состоит из двух подпространств. Это подпространства замкнутых путей и разомкнутых путей. Их размерность меняется при изменении структуры. В двойственных сетях сумма размерности подпространств замкнутых путей и разомкнутых путей постоянна при изменении структуры.

В замкнутой системе с базисом контуров воздействие поперечная величина, а отклик -продольная величина. В открытой системе с базисом разомкнутых путей воздействие продольная величина, а отклик – поперечная величина. Продольная величина измеряется в одной точке, поперечная – как разность измерений в двух точках [11].

Двойственные сети

Суть науки , как представляется, отразил китайский философ.

Величайшая радость наполнит вас, только если вы способны сделать что-то, что нельзя свести к товару. Лао Цзы . Ученый подобен монаху - отказавшись от суеты, он должен постигать мир и добывать новое знание. Вместе с тем М.Фарадей ответил на вопрос о пользе электричества: «Возможно, вы сможете обложить это налогом».

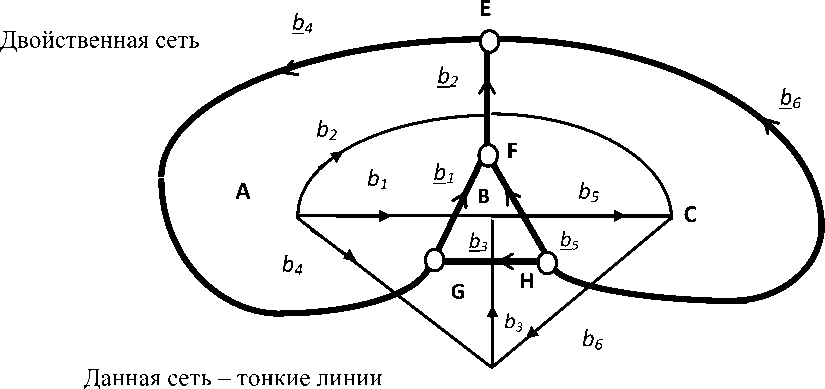
Напомним суть двойственных сетей, и связанный с ними инвариант двойственности. Двойственные сети связывают метрику и структуру. Замкнутому пути в данной сети соответствует разомкнутый путь в двойственной сети. Разомкнутому пути в данной сети соответствует замкнутый путь в двойственной сети. Пример взаимно двойственных сетей представлен на рисунке [8].

D

Рис. 1. Две двойственные сети из 6 ветвей