Phase reconstruction using a Zernike decomposition filter

Coherent wavefronts are analysed using a Zernike filter that decomposes the analyzed light field into a set of diffraction orders with amplitudes proportional to the circular Zernike polynomials. We also apply the algorithm to the calculation of the light field phase from measurements of the modules of decomposition coefficients. Operation of several filter is simulated.

/. Introduction

Reconstruction of die coherent light field phase is a topical problem in digital data processing. We cannot directly measure the light field phase but have to determine it indirectly, via light intensity measurements. For example, the wavefront of the light field can be reconstructed from an interferogram [1], from measurements of the intensity distribution of the spatial Fourier-spectnim [2]. A Shack-Hartmann wavefront sensor consisting of an array of equivalent pinholes or a microlens matrix [3] lias also found use for phase retrieval. One can also reconstruct the phase using amplitude and phase filters capable of decomposing the light field in an orthogonal basis [4,5]. Paper [6] deals with the theory of spatial filters, called modans. intended for analyzing (selecting) the spatial modes of laser light. The number of basis terms that can provide the effective analysis of light fields is minimized using a basis matched to the field under analysis.

Paper [7] suggests dial wavefront aberrations should be analyzed using Zernike polynomials [8]. Note, however, that it turns out to be impossible to design a spatial filter dial would be able to produce an intensity distribution proportional to the coefficients expansion of the sought light field phase in terms of Zernike polynomials. In other words, we cannot solve the formulated problem using a purely optical approach We will have to do additional calculations.

In Ref. [7] an iterative algorithm for calculating the phase of the light field complex amplitude was developed.

In the present paper we compare the results of phase retrieval obtained by the iterative algorithm proposed in Ref. [7] and by the noniterative method considered in Ref. [5].

• 2.    ZERNIKE decomposition coefficients

There is complete set of orthogonal functions with angular harmonics in the circle of radius r₀. These are the circular Zernike polynomials [8]:

^(r, (fl = А,„К™ (r) expOw^),             (1)

where

4m

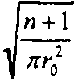
(m- m)/ 2

я,7(0 = I (-D^-Pllx p-0

R^r^are the radial Zernike polynomials:

VW=r:W, r^-i,

R^., W = O^"*¹ (r) = 0^ <  n^w = 1, (r, pi are polar coordinates.

Tlie decomposition of die light complex amplitude E(r, p) into a series in terms of (1) is given by

E^^ ^^.„Дг^, л^О m=-n

I R" (r) R” (r)rdr = —— 3_nD,                  (5)

" p 2(л + 1) np

C_m = П EV^L (r, yydrdtp .              (6)

о 0

In the plane of a spatial Fourier-spectrum which can be generated using a spherical lens with focal length f the light field complex amplitude F(pO) will take the form к r°2*' ^(Ав)-—Jj£(r,#»x ля3 0 0

к           1

xexp -i—rpcos(

L /          J

where k=2n/X is the wavenumber of light, X is die wavelength of light, and (p 6) are polar coordinates Based on Eq. (4), we can represent the decomposition of the light field in (7) into a series in terms of Zernike polynomials in Eq. (I) as:

F(p,ei = y£ I HW/ y:w^-r_Pydr J n-Qm- n o ’

(S)

In deriving Eq. (8) we employed an integral representation of the Bessel function of first kind and of m-th order:

J_m (x) = — | exp[- /xcos t + imt pz.

We can find the integral in Eq. (8) in an explicit form [8]

r°               к wn^pV\^WmkypW^

_ , m) 2 2 ^ ^rtiP) (kf V_cp)

From Eq.(9) it is seen that at n^O the complex amplitude is equal to zero at the central point p 0;

и^р^

o^>o h 2 n . 12 r° ^ = °

(IO)

Therefore, at n>0 die intensity distribution of basis diffraction orders in the Fourier plane will have a like-ring structure.

In Fig. I is shown an optical setup (Zemike’s analyzer) demonstrating the use of a phase Zernike filter for analysis of the wavefront with complex amplitude Efr.tp) Analogous to the wavefront Shack-Hartmann sensor [3). the Zernike filter (ZF) is placed immediately in the plane of the wavefront under study A spherical lens L of focal length / is place beside it. In the rear focal plane of the lens L we place an array of photoreceivers PA coupled to the computer PC.

Mg. I Optical setup

The transmission function of the ZF should be the phase one т{г,(р) =exp|/X(r.^)]                       (ID and is sought-for in the form

^(r^) = £ ^H^tr.^x n-Om n                       ,               (12)

x exp\ikf ¹ rp^ cos(

where (p™, tp^ arc the vectors of carrier spatial frequencies in polar coordinates and v^ orc the task s free parameters dial should be fitted in such a maimer dial Eq. (12) be the correct equality.

Provided the effective spatial separation in die Fourier plane of separate basis diffraction orders, wc can consider the functions lP,^ (r.^exp^/ xrpnm cos(p- Onm) + !„, ] as being nearly orthogonal and compute the parameters in Eq (12) by

( H 2»

j J cxpl/Str.^jr^fr.^) ✓ о 0

X exp[- ikf ^xrp_nm cos(p- 0_nm )]rr/rrAp}

The Zernike filter of Eq (12) produces the spatial separation of certain coefficients C^ from the expansion of the field E(r,tp) in Eq (4). If such a filter т<хл / is placed near a spherical lens and is illuminated by a light wave of amplitude Егх.ул the light intensity at the focal plane points u-a_nm and r - A^ will be approximately proportional to the squared modulus of the expansion coefficients C,„.

kt ‘ | | EU. vyr(x. i)cxp[- ikf (кг-rDpwA ~

-££<’„„ cxp(/ vn„ )3(и-а^л - A„ I л C m n where (o^.. A.P arc the sectors of spatial carrier frequencies in Cartesian coordinates Pic more effect rich is performed the spatial separation of basis beams propagating at different angles, the more accurate will be the approximate equality (14)

• 3.    Iterative algorithm of the light field phase reconstruction

After the light intensity proportional to the squared modules of coefficients of the expansion (4)

Л^^Г                  (15)

has been measured at discrete points of the Fourier-plane (Fig. 1), we will have to do additional calculations to find the light field phase

0(r,^) = argE(r,^).

For this purpose, we may use an iterative algorithm similar to the algorithm of Eqs.(13) and (14). In this case, the estimate of the light field phase in the

^+/>-th iteration will be given by

Qk^»V> =

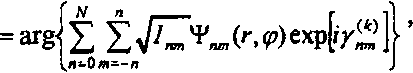
where y^ ^are ^e free parameters in the к -th iteration obtained from die equation

= arg< J |ехр[/£Дг,р)]Т^^        (18)

о 0                                                    I where Qk(r,^ is the desired phase estimation in the к -th iteration.

• 4.    Method of coefficients phase definition Thus, the intensity at points of spatial frequencies (p„m, 9™m) is proportional to the squared amplitude of expansion coefficients, I_nm «(C^j . The phase Фпт = ^arg(C_m,)may be reconstructed if one adds into the filter (7) terms in the form of linear combination of neighboring basis functions [5]:

s_w (^, ^)=fc o-, ^)+ t;_v (r, ф^х x^ikf-'rp^ cos(p-^)+ v^J P пт (Г,ф) = (Т™ (Г, ф) + i4?^ fr, ^)}x xexp^'¹^cos(p-C)+v^j

In this case, the additional channels corresponding to the Fourier-spectrum points with spatial frequency (p*^ 0'^) and (p"^, 6”^) the intensity will be given by: s„ =|фà +|c,.,.|² +2|C,„jC,_w|cos(^,. -O P„ =|C„|^! + |C.vf +2|C„|C„.„.|sin^,,. -,#„). thus making it possible to find the phase ф^, assuming фтгЮ.

The recursive relationship for the sought-for phases may be written in various forms. In view of assumed smallness of certain coefficients, the following function may be used:

ф.. tan"' ^^—^      (21)

i n tn     ' пт              I                                                   ^x

\ "^m    nm ^nm' J

Thus, an optical method provides a sufficient accuracy in finding the complex coefficients of the light field from an orthogonal basis, and reconstructing this field.

• 5.    Numerals examples

The simulation parameters are: 256 pixels on radius r and 256 pixels on angle 0. r₀=l mm, k=10⁴mm\ f=100 mm.

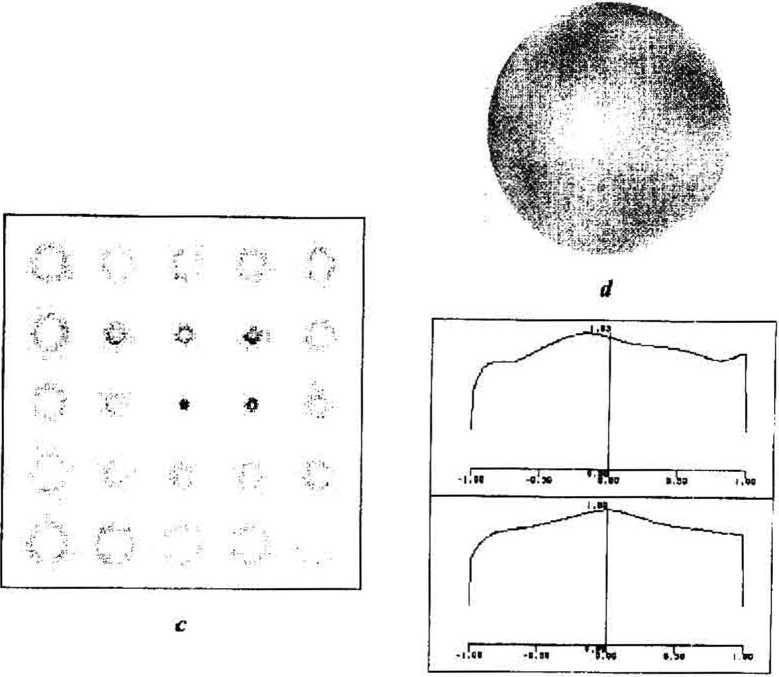
Using the iterative algorithm described in section 3 we designed a 25-channel Zernike filter forming the basis diffraction orders (n,m) at m<& and n 58 that propagate at some angles to the optical axis. Shown in Fig. 2 are: a half-tonic amplitude (a) and phase (b) of the Zernike filter (black colour - phase 0 and white colour - phase 2л) and the configuration of the numbers (n,m) and linear combinations distribution between the orders (c).

(7,1)	(6,6)	(6,4)	(6^>	(6,0)
(73)	(3,1)	(2,2)	(2,Q)	(5,5)
(7,5)	03)	(0,0)	03)	(53)
(7,7)	(4,0)	(4.2)	(M	(5Д)
(8,0)	(8,2)	^	(8,6)	№

Fig. 2 Amplitude antiphase of a 25rchannel Zernike filer for 25 polynomials

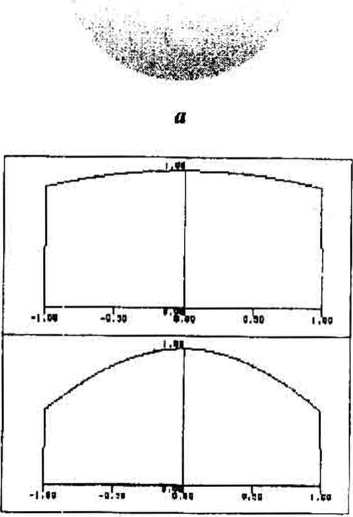
Figure 3 shows the result of operation of the phase-only 25-channel Zernike filter illuminated by a beam:

E(x, У) = exp[i cos(ax+6y)], the beam parameters are chosen to be a=0.5,6=1

In Fig.3 are shown: the illuminating beam phase (a) with cross-sections along the x- and у-axis (b), the diffraction pattern in the Fourier-plane for a phase-only filter (c), the reconstructed light field using the iterative algorithm (d) with cross-sections on axis x and у (e).

In Fig.3 are shown: the illuminating beam phase (a) with cross-sections along the x- (top) and y-axis (bottom) (b), the diffraction pattern in the Fourier-plane for a phase-only filter (c), the light field reconstructed using the iterative algorithm (d) with cross-sections along the x- (top) andy-axis (bottom) (e).

е

Fig. 3. Result of phase reconstruction using the iterative algorithm

Figure 4 depicts how the r.ms. error of reconstruction, 5, depends on the number of iterations k, Eq. (17). One can see that if one uses a phase-only filter the process steadily converges during 100 iterations, although any acceptable reconstruction error is not achieved (5>0.2). Note that the use of an amplitude-phase filter (Fig. 2a,b) resulted in the fast convergence

for a amplitude-phase filter (ft), die reconstructed light field using method (21) (d) with cross-sections along the x- (top) andy-axis (bottom) (e).

(after 5 iterations) of the process of reconstructing the

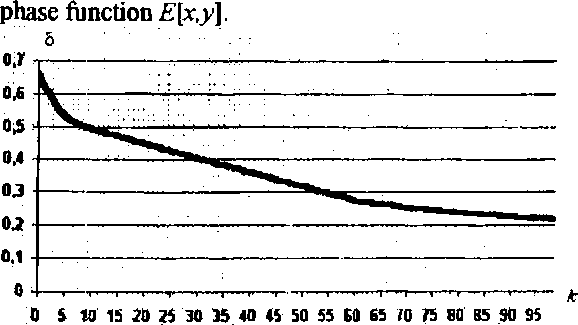
Fig. 4. Rm.s error of reconstruction 5 vs the number of iterations

S6 i S5

S4

SR , $7

Pl

P2

0,1) i (22) (2,0)

(33) I (0,0)

(1,1)

S3

S2

P3 (4,0) (433 (4,4) SI

P4 P5

Using the method described in section 4 we designed a 25-channel Zemike filter forming the basis diffraction orders (n,m) at n<4 and m<4 (total 9) and their linear combination (total 8+8) that propagate at some angles to the optical axis. Shown in Fig. 5 are: a half-tonic amplitude (a) and phase (b) of the Zemike filter and the configuration of the numbers (n.m) and linear combinations distribution between the orders (c).

In Fig.6 are shown: the illuminating beam phase (a) with cross-sections along the x- (top) and y-axis (bottom) (b), the diffraction pattern in the Fourier-plane

P6 i P7 P8 I

Fig. S. .Amplitude antiphase of a 25-channel Zernike filler for 9 polynomials

In this case, a tolerable reconstruction of the phase took place only with the use of an amplitude-pliasc filter, the r.m.s. error being 6=0.14. From Fig. 6, the phase is seen to be reconstructed up to a turn. A subsequent application of the iterative algorithm (17)-(!8) did not result in the decreasing error. In all cases the process diverged at once.

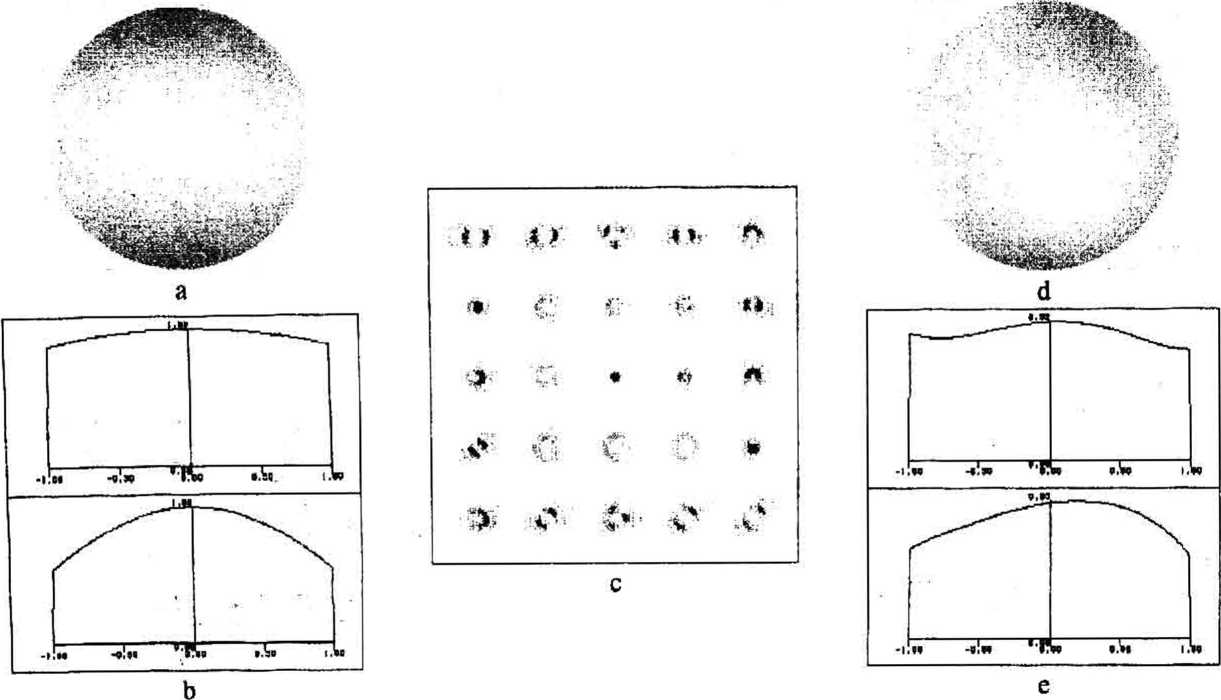
Fig. 6 Result of phase reconstruction using method (21)

• 6.    Conclusions

The results obtained allow us to infer that the light field phase is possible to reconstruct using a filter matched to Zernike polynomials. In the present context, the method (21) has been shown to be better than the iterative algorithm (17)-(18).

Acknowledgments

This work was supported by Russian Foundation of Fundamental Research (№№ 96-01-10021, 98-01-00894).