Piecewise approximation based on nonparametric modeling algorithms
Автор: E. D. Mikhov
Журнал: Siberian Aerospace Journal @vestnik-sibsau-en
Рубрика: Informatics, computer technology and management
Статья в выпуске: 2 vol.21, 2020 года.
Бесплатный доступ
In this research the issue of inertialess processes modeling is under study. The main modeling algorithm is the non-parametric recovery algorithm of the regression function. The algorithm allows to build a process model under conditions of low a priori information. This feature may be particularly important in modeling processes of large dimensions prevailing in the space industry. One important feature of the algorithm for nonparametric estimation of the regression function is that the accuracy of modeling using this algorithm highly depends on the quality of the observations sample. Due to the fact that in processes with large dimensions of input and output variable vectors observation sampling elements are in most cases unevenly distributed, the development of modifications to improve the quality of mod-eling is relevant. The modification of the nonparametric dual algorithm based on piecewise approximations has been devel-oped. According to the proposed modification, the process area is divided into sub-areas and a non-parametric esti-mate of the regression function for each of these sub-areas is recovered. The proposed modification reduces the impact of some observation sampling features, such as sparseness or voids in observation samples on the quality of the built model. The computational experiments were carried out, during which a comparison was made between the classical algorithm of non-parametric estimation of regression function and the developed modification. As the computa-tional experiments have shown, with uniform distribution of the sample elements of observations, the developed modification does not lead to the improvement of the quality of modeling. With a substantial uneven distribution of the observations sample elements, the developed modification resulted in a 2-fold improvement in the quality of the simulation. The results suggest that the proposed modification can be used to model complex technologi-cal processes, including those in the space industry.
Identification, nonparametric estimation of the regression function, piecewise approximation.
Короткий адрес: https://sciup.org/148321737
IDR: 148321737 | УДК: 519.87 | DOI: 10.31772/2587-6066-2020-21-2-195-200
Текст научной статьи Piecewise approximation based on nonparametric modeling algorithms
Introduction. The article studies the problem of inertialess technological processes identification.
The scheme of the simulated process is shown in the fig. 1 [1].
The following notations are used in fig. 1: u(t ) - input variables vector; x ( t ) - output variables vector; ξ ( t ) – interference effect; О – process.
The main modeling algorithm is the nonparametric regression function recovery algorithm [2–5], and piecewise-defined approximations [6–8].
When getting a sample of observations, not only the sample of observations size is important, but also its quality. The quality of a sample of observations is the accuracy of parameters readout, the presence of outliers in it, the uniformity of the distribution of the sample of observations, etc.
Special attention is paid to the problem of modeling the process with an uneven distribution of the sample of observations [9–11].
In some tasks, a sample of observations can be distributed over an area where the process Q ( u, x ) occurs with sparseness, voids, or concentration of the sample of observations elements. As an example, fig. 2 shows an unevenly distributed sample of observations.
In fig. 2, the area 1 contains the so-called sparseness in the observation samples, number 2 denotes voids in space Q ( u, x ), and number 3 denotes the elements of the observation sample.
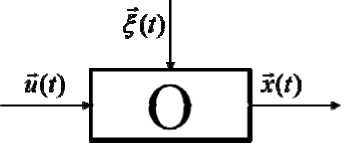
Fig. 1. The simulated process
Рис. 1. Моделируемый процесс
For nonparametric estimation of the regression function, the quality of the sample of observations is of particular importance. With an uneven distribution of the observations sample there arises the difficulty in setting up the blur parameters c s vector, as some areas are sparse and it is assumed that in such cases c s should be large, and in some areas there is concentration and it is assumed that for these cases c s should get a small value. Undoubtedly, all this also affects the quality of the resulting model.
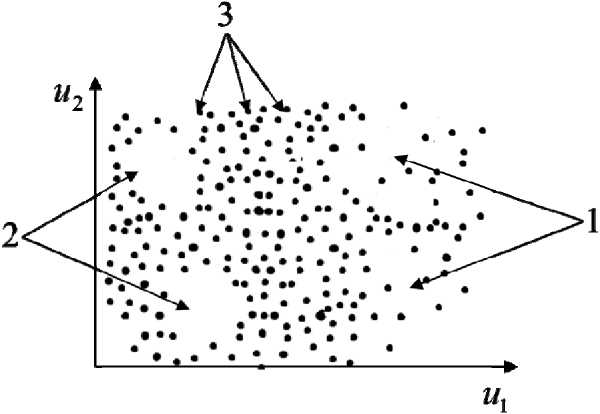
Fig. 2. Uneven sample of observations
Рис. 2. Неравномерно распределенная выборка наблюдений
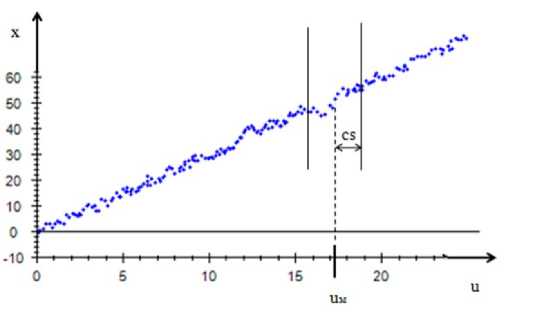
Fig. 3. Determination of blur parameter
Рис. 3. Определение параметра размытости
The process of building a mathematical model of the technological process shown in fig. 1 can be divided into several consecutive stages:
-
1) getting a priori information about the process;
-
2) getting a sample of observations;
-
3) choosing a metod of building a mathematical model;
-
4) building a mathematical model.
The article focuses on the stage of choosing a method for constructing a mathematical model.
Nonparametric recovery of the regression function. “Parametric approach” implies that the structure of the process or object under study is known, but the parameters of this structure are not known.
The type of algorithm used depends on the level of a priori information. If a priori information is sufficient to select the object structure, then parametric algorithms can be used.
Nonparametric identification is generally implemented using a nonparametric estimation of the regression function.
s
n
Z «П*
u
^^^^^^B
u
x s ( u s ) =
i = 1
j’ = 1
cs
sn zn i =1 j =1
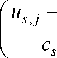
In (1) the following notations are used: Ф(*) – is a bell-shaped smoothing function; с s – is the blur parameter.
The quality of the built model directly depends on the chosen blur parameter с jx . This coefficient determines the degree of participation of the sample elements in the calculation of xs at the u м point.
As shown in fig. 3, only those variables that have |u – u м | < c s participate in building the model at the u м point, and the closer | u – uм | is to zero, the more influence this point has on the results of calculations.
In nonparametric estimation of the regression function, the quality of the sample of observations is of particular importance. Of course, for any model, the quality of the sample of observations also affects the accuracy of
the constructed model, but in the case of nonparametric estimation of the regression function, this is of particular importance.
Piecewise-defined approximation One of the options for building a mathematical model of the process the ideas of which will be further used is a piecewise-defined approximation.
The idea of a piecewise-defined approximation is to divide the Omega area into some sub-areas Q, ( u), i = 1, m (fig. 4), and to build for each area Q;( u) its own mathematical model of the process.
One of the most well-known piecewise-defined approximations are spline functions. The advantage of this approach is that unevenness of the sample of observations does not have a big impact on the quality of the model. The weak side of spline functions is that it is quite difficult to select a function and set parameters for each area Q; ( u) for the tasks of large dimensions.
The developed modification of the nonparametric estimation of the regression function. The complexity of nonparametric estimation of the regression function, in contrast to spline functions, increases much more slowly. In this regard, it seems logical to combine the idea of a piecewise-defined approximation and a nonparametric estimation of the regression function.
The following modification of the nonparametric estimation of the regression function has been developed:
The stage of building the model:
-
1) omega area is divided into sub-areas Q;( u) ;
-
2) for each areaQ;( u) , the regression function is recovered using a nonparametric estimation of the regression function;
-
3) the blur vector is being set for each area Q;( u) [12].
The stage of making a forecast at point u :
-
1) the area Q, ( u) to which the point u belongs is defined;
-
2) the regression function is recovered using the set vector of blur parameters for the area Q, ( u) .
Sub-areas Q i ( u) can be split by various methods. It is possible to apply the algorithms for splitting samples into classes, or choose the classic way for splines and split the entire area of input variables definition into equal parts and set the vector of blur parameters for each of them.
Computational experiments. The numerical experiments were performed comparing the classical nonparametric estimation of the regression function with the proposed modification. Numerical experiments were performed for several cases that differ in the uneven distribution of the components of the observation samples.
First of all, an experiment was conducted to model an object described by the following equation:
f ( «) = f ( u 1 , u 2 , u 3 , u 4 , u 5 , u 6 ) = (2) = 6sin( u 1 ) + 2 u 2 + u 3 / 6 + 4cos( u 4 ) + u 5 - 8 u 6 .
It should be noted that the algorithm for the regression function recovery does not identify the type of equation. The equation is only used for generating a sample of observations.
The following initial data were taken for the experiment: the size of the sample of observations s = 4000; the amount of interference affecting the object
£ = 4%; й e (0;3); the elements of the sample of observations are distributed evenly.
The model will be constructed using an algorithm for nonparametric estimation of the regression function and using the proposed modification of the algorithm.
The simulation results are shown in tab. 1
According to the results of the experiment, the average forecast error in the modified algorithm slightly decreased, as well as the time for setting the blur parameters and the speed of making the forecast increased.
This experiment showed that if the sample of observations is uniformly distributed, it is not necessary to divide the elements of the sample of observations into classes. Here we would like to note that the considered case is quite rare in practice. The sample almost always has concentration or sparseness.
In the next numerical experiment, the sample of observations will have sparseness and concentration of the elements of the sample of observations.
The results of object modeling under these conditions are summarized in tab. 2.
Fig. 4. Split of Q i ( u ) into sub-areas Q i ( u)
Рис. 4. Разбиение Q i ( u ) на подобласти Q i ( й)
Table 1
The results of the regression function recovery
|
Nonparametric algorithm for the regression function recovery |
Modified nonparametric algorithm for the regression function recovery |
|
|
Average forecast error, % |
3 |
4 |
|
Blur paramerers setting time, ms |
30 |
70 |
|
Forecasting speed, ms |
45 |
69 |
The results of the regression function recovery
Table 2
|
Nonparametric algorithm for the regression function recovery |
Modified nonparametric algorithm for the regression function recovery |
|
|
Average forecast error, % |
14 |
7 |
|
Blur paramerers setting time, ms |
35 |
70 |
|
Forecasting speed, ms |
52 |
84 |
The results of the regression function recovery
Table 3
|
Nonparametric algorithm for the regression function recovery |
Modified nonparametric algorithm for the regression function recovery |
|
|
Average forecast error, % |
23 |
8 |
|
Blur paramerers setting time, ms |
36 |
69 |
|
Forecasting speed, ms |
49 |
78 |
According to the experiment, the difference between the average simulation error of the classical algorithm for nonparametric estimation of the regression function and the proposed modification is higher than in the experiment shown in tab. 1. Based on this, we can conclude that when heterogeneity appears in the sample of observations, the proposed modification allows us to estimate the regression function more accurately.
To confirm this assumption, another experiment was conducted, which introduced an even greater heterogeneity in the observation sample than in the experiment shown in tab. 2.
The results of this experiment are summarized in tab. 3.
As can be concluded from tab. 3, when the uneven distribution of the sample of observations elements increases, the accuracy of the proposed modification becomes higher than the accuracy of the classical algorithm.
It is important to note that unevenness in the sample of observations is ubiquitous when modeling objects with large input-output dimensions.
Conclusion. The modification of the algorithm for nonparametric recovery of the regression function has been developed. The modification consists in using the idea of piecewise-defined approximations and splitting the modeling area into sub-areas, for each of them the regression function is separately recovered .
During the computational experiments, it was demonstrated that the proposed modification significantly improves the quality of modeling the process when the elements of the sample of observations are distributed unevenly, there are sparseness and voids in the sample of observations. It is important to note that there are other methods for dealing with an unevenly distributed sample of observations [13–15].
Acknowledgment. This work was financially supported by the Ministry of Science and Higher Education of the Russian Federation in the implementation of the integrated project “Creation of a production of earth stations of advanced satellite communications systems to ensure the coherence of hard, northern and Arctic territory of Russian Federation”, implemented with the participation of the Siberian Federal University (agreement number 075-11-2019-078 dated 13.12.2019).
Список литературы Piecewise approximation based on nonparametric modeling algorithms
- Medvedev A. V., Mihov E. D., Ivanov N. D. Identification of multidimensional technological processes with dependent input variables. Journal of the Siberian Federal University. Series: Mathematics and Physics. 2018, Vol. 11, No. 5, P. 649–658.
- Kornet M. E., Shishkina A. V. About the identification of dynamic systems under nonparametric uncertainty. Aspire to Science. 2018, P. 166–170.
- Lapko A. V., Lapko V. A. Multilevel nonparametric information processing systems. Krasnoyarsk : SibGAU, 2013. 270 p. (In Russ.)
- Medvedev A. V. Some remarks on the theory of non-parametric systems. Applied Methods of Statistical Analysis. 2017, P. 72–81.
- Medvedev A. V., Raskina A. V., Chzhan E. A., Korneeva A. A., Videnin C. A. Determination of the order of stochastically linear dynamic systems by using non-parametric estimation of a regression function. Journal of Physics: Conference Series. Krasnoyarsk Science and Technology City Hall of the Russian Union of Scientific and Engineering Associations; Polytechnical Institute of Siberian Federal University. Bristol, United Kingdom. 2019, P. 1–8.
- Reisinger C., Forsyth P. A. Piecewise constant policy approximations to Hamilton–Jacobi–Bellman equations. Applied Numerical Mathematics. 2016, Vol. 103, P. 27–47.
- Gaudioso M., Giallombardo G., Miglionico G., Bagirov A. M. Minimizing nonsmooth DC functions via successive DC piecewise-affine approximations. Journal of Global Optimization. 2018, Vol. 71, P 37–55.
- Liu J., Bynum M., Castillo A., Watsonb J., Lairda C. D. A multitree approach for global solution of ACOPF problems using piecewise outer approximations. Computers & Chemical Engineering. 2018, Vol. 114, P. 145–157.
- Medvedev A. V., Meleh D. A., Sergeeva N. A., Chubarova O. V. [On the problem of classifying objects by data with gaps]. Information Technology and Mathematical Modeling (ITMM-2019). P. 146–151 (In Russ.).
- Chzhan E. A., Medvedev A. V., Kukartsev V. V. Nonparametric modelling of multidimensional technological processes with dependent variables. IOP Conference Series: Earth and Environmental Science. 2018, P. 1–5.
- Paul S., Shankar S. On estimating efficiency effects in a stochastic frontier model. European Journal of Operational Research. 2018, Vol. 271, Iss. 2, P. 769–774.
- Mikhov E. D. [Core blur coefficient optimization in nonparametric modeling]. Vestnik SibGAU. 2015, Vol. 16, No. 2, P. 338–342 (In Russ.).
- Medvedev A. V., Chzhan E. A. [Modeling of multidimensional H-processes]. Information and mathematical technologies in science and management. 2018, No. 1 (9), P. 99–105 (In Russ.).
- Simar L., Keilegom I., Zelenyuk V. Nonparametric least squares methods for stochastic frontier models. Journal of Productivity Analysis. 2017, Vol. 47, P. 189–204.
- Zhang C., Travis D. Gaps‐fill of SLC‐off Landsat ETM+ satellite image using a geostatistical approach. International Journal of Remote Sensing. 2007, Vol. 28, Iss. 22, P. 5103–5122.


